针对几种元启发式算法的应用性能对比研究

尚正阳，顾寄南，唐仕喜，孙晓红

（1.安徽工程大学机械与汽车工程学院，安徽 芜湖 241000；2.江苏大学制造业信息化研究中心，江苏 镇江 212000）

1 引言

启发式算法（heuristic algorithm）是一种根据人为经验或者自然规律所构造的算法，它能够在可接受的计算花费下给出一个较优的可行解。现阶段，由于元启发式算法（meta-heuristic）具有较少依赖算法本身组织结构的特点，其通用性强、泛化性好，已经被广泛应用在了实际生产和生活的各个领域。特别是针对工业中大量存在的NP-hard 问题，元启发式算法已成为求解此类问题的主要途径。在此，将针对具有代表性的四种算法：遗传算法（Genetic Algorithm，简称GA）、模拟退火算法（Simulated annealing algorithm，简称SA）、禁忌搜索算法（Tabu Search，简称TS）和蚁群算法（Ant Colony Optimization，简称ACO）进行基于其应用性能的对比分析。其中，遗传算法于1975 年被文献[1]提出，它借鉴了生物的进化过程，能够按照优胜略汰的原则对群体目标进行逐代演化；模拟退火算法于1953 年被文献[2]提出，它模拟了固体退火原理，能够通过对新解的动态概率接收来获得一个较优解；禁忌搜索算法于1986 年被文献[3]提出，它模拟了人类记忆过程，通过引入禁忌表来避免迂回搜索实现全局优化；蚁群算法于1992 年被文献[4]提出，该算法模拟了蚂蚁寻食过程中的路径发现行为，能够在正反馈机制的作用下逐渐增加对较优解的获得概率。以上四种元启发式算法，由于具有较好的适应性和求解效果，已经在路径规划[5-6]，资源调度[7-8]和参数优化[9-10]等多个方面得到了普遍应用。除此之外，为提高针对特定对象的优化能力，算法之间也能够通过模块耦合来实现其功能上的互补，例如混合遗传模拟退火算法[11-12]，遗传蚁群算法[13-14]，模拟退火蚁群算法[15-16]等。所以对于相关算法求解过程和求解效果的研究就尤为重要，它是实现具体工程问题高效求解的关键。然而，正是由于启发式算法的“仿生”特性，对其求解性能的描述往往停留在认知层面，缺少具体的对比和论证。特别是在实际应用中，相关算法的选择往往依靠人为经验，同一问题能够被不同学者结合不同算法进行求解。所以，对于以上四种算法的对比分析，不仅能够明确其各自的特点属性，还能够为相关算法的合理选择和性能改进提供基础与参考。

2 算法解析

通常，实际问题被转化为序列的组合优化问题进行求解，而元启发式算法就是要在有限的计算消耗中，找到一个较优的可行解。其中，这个排列组合被称为解，由排列组合代入实际问题所计算出的结果被称为适应度。总的来看，元启发式算法的优化机理，如图1 所示。

图1 元启发式算法优化机理Fig.1 Optimization Mechanism of the Meta-Heuristic Algorithm

算法通过不断的对单个或者多个解（包括初始解）的邻域结构改变来形成新解，并进一步的通过对新解的接受与筛选生成更优解。在这个循环迭代过程中，最核心的内容是新解的产生方法和更优解的接受原则（分别如图1 中的方形虚线和圆形虚线所示），它们决定了整个算法的工作原理与操作方式。值得注意的是，虽然针对不同问题，同一算法的新解产生方法和更优解接受原则不尽相同，但是其整体的求解特性并未改变。所以为了便于分析，以最为基础且通用的组织方式来构建算法，旨在实现对以上四种元启发式算法求解性能的直观比较。

2.1 遗传算法

遗传算法主要包括交叉操作、变异操作和选择操作三个部分。其中，变异和交叉是种群产生新解的具体方法，而选择则包含了更优解的接受原则。在执行过程中，变异为选择提供资料，交叉用于巩固选择结果，选择则能够引导变异和交叉朝着适应“环境”的方向发展。

在实验中，交叉操作，如图2 所示。两个父代的第3 到第5号位置需要进行交换，在此采用循环的方式进行逐个改变。特别的，每当两个位置的数值交换后，还应对数列中的重复数字进行调整。变异操作，如图3 所示。突变发生在单个父代序列的3 号和6 号位置，这两个位置中的数值进行交换。而选择操作则设置为常规的赌轮盘方式。

图2 交叉操作Fig.2 Cross Operation

图3 变异操作Fig.3 Mutation Operation

2.2 模拟退火算法

模拟退火算法源于固体退火原理：高温固体在冷却过程中，所包含粒子在每个时刻都极力趋向平衡态，其能量随温度的降低而逐渐减少，直至常温达到基态。在此过程中，新解的产生通常采用随机的邻域改变方法，而对更优解的接受则完全模拟了固体的退火过程，即算法执行前期以较大概率接受一个非更优解为更优解，从而保证算法的全局搜索能力，而在执行后期则以较小概率对非更优解进行接受，用以保留当前已获得的相对较优解。其中，接受概率随“退火温度”的改变而逐渐变小。

2.3 禁忌搜索算法

禁忌搜索算法模拟了人类记忆过程，其中新解产生采用了随机的邻域结构改变方法，而对新解搜索则引入了禁忌表，禁忌表能够记录已搜索过的较好邻域结构，从而在下次迭代中主动避开已记录的邻域移动，减少重复操作。对于更优解的接受原则则通常采取贪婪的择优选取方法。从新解产生和更优解接受的角度上看，遗传算法和模拟退火算法的主要操作来自于对更优解的接受，而禁忌搜索和蚁群算法的关键则在于对新解的产生和搜索，这是它们之间的最大不同。

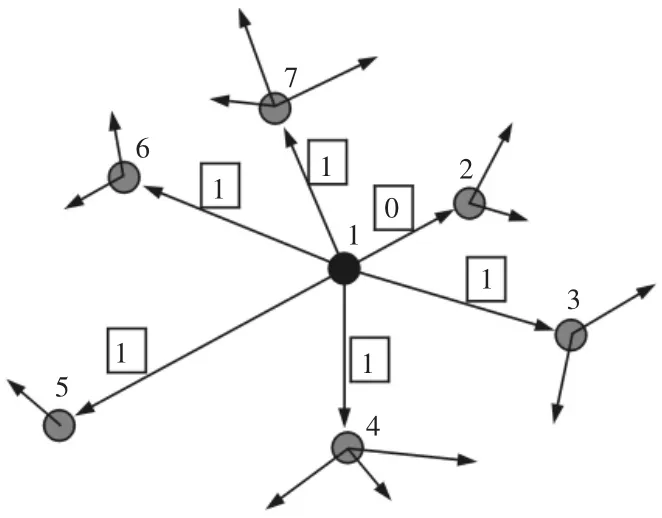
图4 禁忌搜索算法原理图例Fig.4 Schematic Illustration of Tabu Search

在一次邻域结构改变中，从位置1 到位置2 为已得到的最短距离，故而将其列入禁忌表暂时禁止（0 表示被禁止选择，1 表示可以被选择），以此来增加算法对其他路径的搜索概率，如图4所示。其中邻域改变的受禁忌范围影响着算法的全局搜索能力，受禁范围小，则搜索范围大收敛速度慢，受禁范围大，则搜索范围小求解精度低。

2.4 蚁群算法

蚁群算法模拟了蚂蚁在寻食过程中的路径发现行为。实际上，它与禁忌搜索算法具有一定的相似性，都能够按照一定规则进行新解的搜索与接受。不同的是，蚁群算法中基于正反馈机制所建立起来的禁忌表，并不单纯的代表着禁止与允许操作，而是能够通过对每一个邻域移动概率的动态更新，来趋向性的引导新解（更优解）产生。

在一次邻域改变中，从位置1 到位置2 的选择概率为1/2，从位置1 到位置3 的选择概率为1/18，以此类推，如图5 所示。这些选择概率能够在每一次迭代中不断积累，从而实现最终较优解的获得。特别的，禁忌搜索和蚁群算法都依赖于禁忌表的建立，故而其优化对象也就要求具有相对稳定且独立的邻域结构。

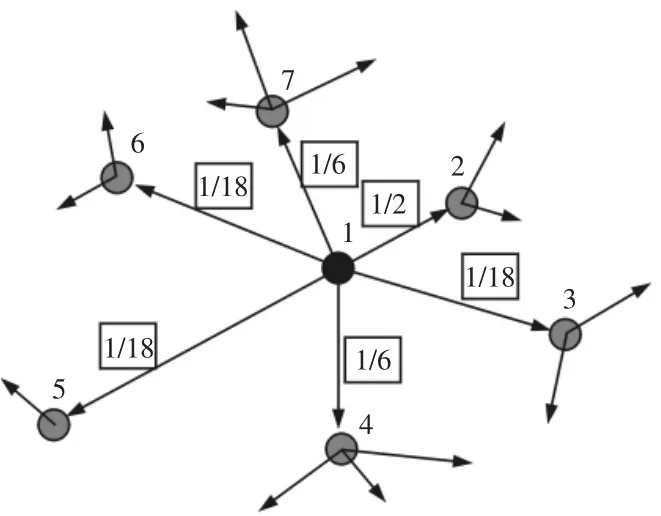
图5 蚁群算法原理图例Fig.5 Schematic Illustration of ACO Algorithm

3 实验与分析

3.1 实验设计

为对比分析遗传、模拟退火、禁忌搜索和蚁群算法的求解性能，在此以典型的序列优化模型—旅行商问题（TSP）为对象，构建实验。其中，TSP 问题是指旅行商人需要经过n个城市并最终回到原点，且每个城市仅能经过一次，其目标是求得一个最短的Hamilton 路径回路。对于n个城市，一共有（n-1）! /2 条可能路径，这是一个典型的NP-hard 问题。

其中，五个不同规模和类型的TSP 算例chn31、eil76、pr152、tsp225、lin318 被进行了测试，它们都来自于国际通用的TSP 测试库[17]。基本参数，如表1 所示。为便于表达和对比，在实验中用相对距离来表示算法的计算结果，相对距离为求解距离与最短距离的比值。

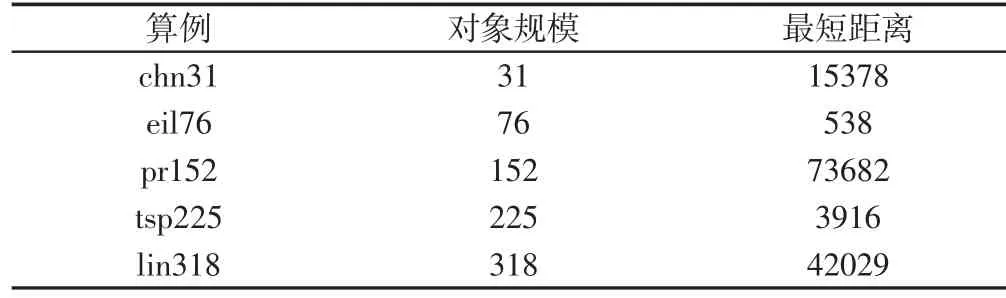
表1 TSP 算例参数Tab.1 Parameters of TSP Instances

在参数设置方面，为体现出不同算法在不同计算维度下的求解效果，在此按照普遍的工程应用经验进行设置，其三种不同规模的参数被列出，如表2 所示。表中：n—目标函数的数列长度，遗传算法发生变异的基因个数为0.05*n，模拟退火算法和禁忌搜索算法采用2-opt 的邻域改变策略。

表2 GA、SA、TS 和ACO 算法的计算参数设置表Tab.2 Parameters Setting for GA，SA，TS and ACO Algorithms

3.2 遗传算法与模拟退火算法

首先，对遗传和模拟退火算法在小计算量、中计算量和大计算量参数下的五个TSP 算例进行测试。实验结果为算法运行20次的平均值。随着计算量的逐渐增大，五个算例的平均求解距离逐渐变小（求解效果逐渐变好），计算时间逐渐增大，说明GA 与SA 的计算精度和运行时间随着计算量的增加而增加，如表3 所示。

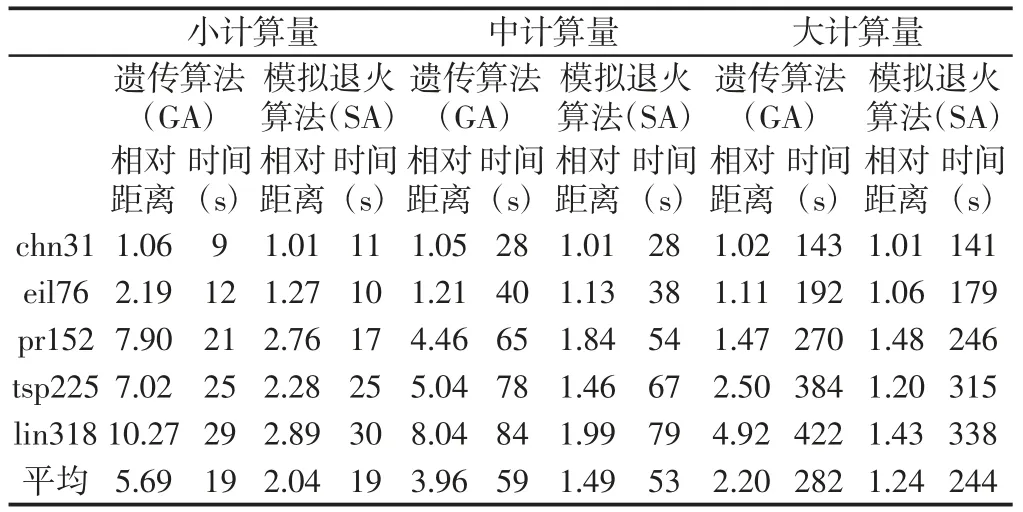
表3 遗传算法与模拟退火算法的计算结果Tab.3 Results of GA and SA

从不同规模的算例求解上看，在小计算量情况下GA 和SA都能对算例chn31 取得不错的解，而对于大规模算例lin318 则需要较大的计算量。说明随着对象规模的递增，算法收敛所需要的计算量也随之增加。特别的，针对不同规模的算例pr152 和tsp225，在中计算量和大计算量条件下，GA 对于pr152 的计算结果是优于tsp225 的，而SA 对于小规模算例pr152 的计算效果反而不如tsp225。这说明基于个体操作的SA 在求解效果上受对象特征影响较大。总的来看，在相同运算时间下SA 对TSP 问题的求解效果普遍优于GA。

为进一步对GA 和SA 的优化性能进行分析，其在大计算量参数下的求解过程被给出，如图6 所示。可见，对于基于种群进化的GA，大型算例pr152、tsp225 和lin318 的优化过程并没有充分收敛，较大的目标算例往往需要较多的迭代次数才能达到较优的求解效果。而对于SA，不同算例的收敛曲线相差较大（多次实验效果类似），这从也另一方面说明了其求解性能受对象特征的影响较大。除此之外，在SA 的求解过程中，无论是大规模算例还是小规模算例，主要优化行为都发生在退火的“高温”和“中温”区域，而在“低温”区域则相对缓慢，所以合适的退火参数选择就对SA 的优化效果至关重要。

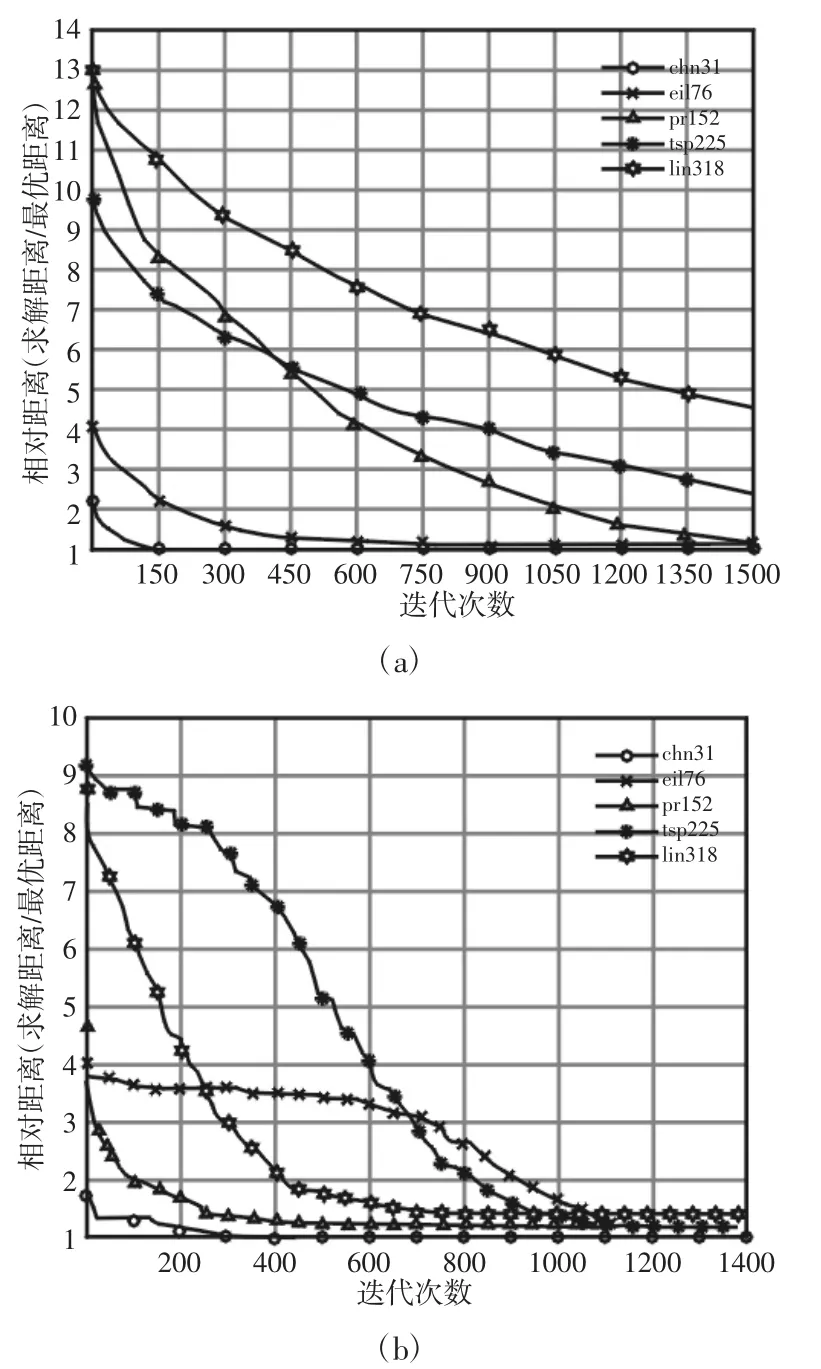
图6 在大计算量条件下的遗传算法（a）和退火算法（b）的求解过程Fig.6 Solving Process of GA（a）and SA（b）in Large-Scale Computing

3.3 禁忌搜索与蚁群算法

在同等实验条件下，禁忌搜索与蚁群算法的计算结果，如表4 所示。由于禁忌搜索和蚁群算法都是基于禁忌表的搜索算法，在此将其对比分析。从整体上看，无论是在小计算量、中计算量还是大计算量的参数设置下，ACO 都能够获得一个较好的求解效果。特别的，即使在小计算量条件下，ACO依然能够针对大规模算例lin318 取得一个不错的解，这是明显优于其他算法的。而针对单个个体优化的Tabu 算法，对小规模算例pr152 的求解效果反而不如大规模算例tsp225，其受对象特征的影响较大。具体Tabu 和ACO 在大计算量参数下的求解过程，如图7 所示。

表4 禁忌搜索算法与蚁群算法的计算结果Tab.4 Results of TS and ACO

Tabu 在迭代过程前期的优化速度较快，但是随着算法的运行其寻优能力逐渐变缓，如图7（a）所示。而对于ACO，它能够快速的得到一个较优解，相对于其他三种算法，ACO 在第一步中就完成了整个优化过程的90%，进而能够在较少的迭代次数下完成计算收敛，如图7（b）所示。

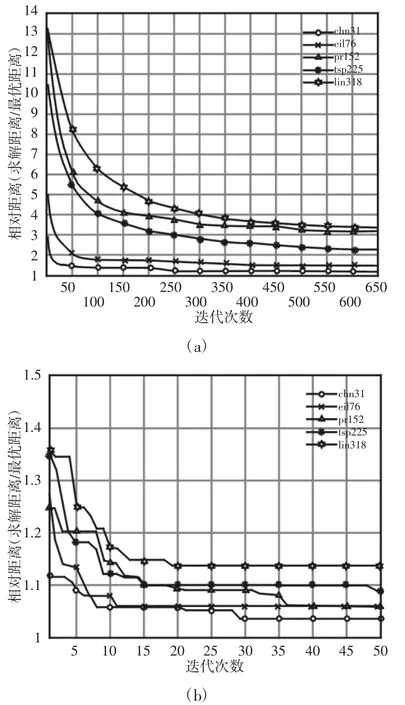
图7 在大计算量条件下的禁忌搜索和蚁群算法求解过程Fig.7 Solving Process of TS（a）and ACO（b）in Large-Scale Computing

3.4 总体实验结果分析

为总体定量的对四种元启发式算法进行对比分析，分别将其在三种不同计算量下的平均运算结果汇总，如表5 所示。

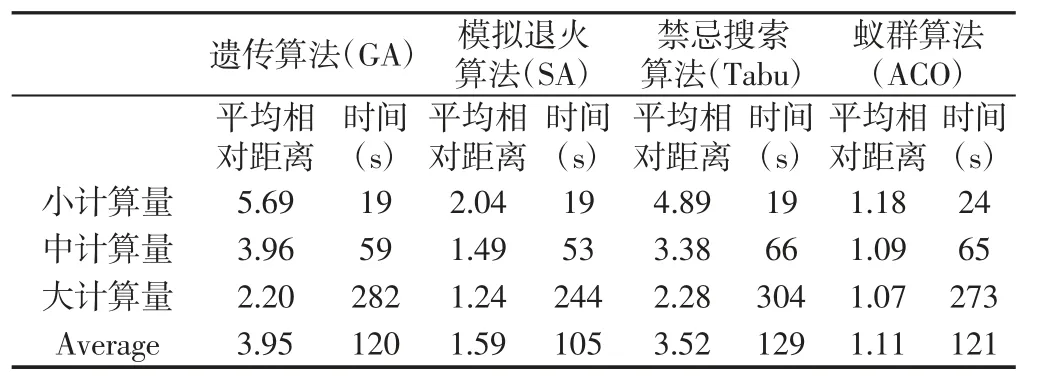
表5 四种算法的总体计算结果Tab.5 Comparative Results on the Algorithms

从求解效果上看，在运算时间相似的情况下，蚁群算法获得了1.11 倍最优路径距离的平均相对距离，优于其他三种算法。特别是在小计算量的参数设置下，其表现依然优秀。模拟退火算法和禁忌搜索算法都是基于单个对象的迭代操作，其在邻域结构较为简单的TSP 问题中也表现出了不错的性能。而遗传算法则表现最差，在平均120s 的时间里获得了3.95 倍的平均相对距离。

4 结论

首先从新解产生方法和更优解接受原则两个方面入手，对遗传、模拟退火、禁忌搜索和蚁群算法进行了解构与分析，指出了其在原理与结构上的异同。之后结合不同规模的TSP 问题构建了多维度的对比实验，通过对算法求解过程和求解效果的深入分析，得到如下结论：（1）GA 是一种基于种群进化的搜索算法，它具有较强的鲁棒性且求解效果稳定。但是收敛速度缓慢，特别是对于大型算例，GA 往往需要更多的运算消耗才能得到一个较优的解。（2）SA 是一种基于单个个体不断变异优选的搜索算法，求解效果受其对象特征的影响较大。所以为了得到更好的计算结果，通常需要根据具体对象进行针对性的邻域结构（新解的产生方法）和退火参数（更优解的接受原则）设计。（3）Tabu 和ACO 都是基于禁忌表的搜索算法，适合应用在具有稳定领域结构（邻域移动能够受禁忌表控制）的优化问题中。实际上，ACO 可以看作是Tabu 算法的改进和扩展，一方面它更新了具有趋向性的概率新解产生方式，加强了算法的全局搜索能力，能够准确并快速的进行求解；另一方面，它相较于Tabu 引入了基于种群的进化模式，有效降低了求解结果受初始解和随机操作等因素的影响。虽然ACO 的构造及参数设置相对复杂，但是其能够在第一次迭代中就找到一个不错的解，执行高效。

所做工作实现了常见四种元启发式算法的定量对比，为相关技术人员的选择、应用和改进提供了基础与参考，具有一定的工程应用价值。进一步的，将扩展算法对比目标，深化算法对比内容，实现更加全面和准确的算法性能解析。