Species-specif ic biomass allometric models and expansion factors for indigenous and planted forests of the Mozambique highlands

Tarquinio Mateus Magalhães ·Victoria Norberto Cossa · Benard Soares Guedes ·Amélia Saraiva Monguela Fanheiro

Abstract Secondary Miombo woodlands and forest plantations occupy increasing areas in Mozambique, the former due to anthropogenic activities. Plantations, mainly species of Eucalyptus and Pinus, are being established on sites previously covered by secondary Miombo woodlands. This aff ects the evolution, cycle and spatiotemporal patterns of carbon (C) storage and stocks in forest ecosystems. The estimation of C storage, which is indispensable for formulating climate change policies on sequestrating CO 2 , requires tools such as biomass models and biomass conversion and expansion factors (BCEF). In Mozambique, these tools are needed for both indigenous forests and plantations. The objective of this study is to f it species-specif ic allometric biomass models and BCEF for exotic and indigenous tree species. To incorporate effi cient inter-species variability, biomass equations were f itted using nonlinear mixed-Effects models. All tree component biomass models had good predictability; however, better predictive accuracy and ability was observed for the 2-predictors biomass model with tree height as a second predictor. The majority of the variability in BCEF was explained by the variation in tree species. Miombo species had larger crown biomass per unit of stem diameter and stored larger amounts of biomass per stem volume. However, due to relatively rapid growth, larger stem diameters,heights, and stand density, the plantations stored more biomass per tree and per unit area.

Introduction

Forests sequester one third of carbon dioxide (CO2) emissions from fuel and land use changes (Houghton 2007; Pan et al. 2011), store large amounts of carbon (C) in vegetation and soils, are sources of C when disturbed or destroyed by anthropogenic or natural causes, and become atmospheric C sinks during forest growth after disturbance (Brown et al.1999). Land use changes are associated with ecosystem C change (Fan et al. 2016) and are the second largest cause of C losses after fossil fuel combustion (Fu et al. 2010; Lozano-García and Parras-Alcántara 2013).

Miombo is the main and most extensive forest type in southern Africa (Ribeiro et al. 2015), and in Mozambique,it comprises about two-thirds of the country´s forested land(Aquino et al. 2018). Secondary Miombo woodlands and forest plantations have been occupying increasing areas in Mozambique, the former due to anthropogenic activities.Plantations, mainly species ofEucalyptusandPinus(Blid 2014), are being established in areas previously occupied by secondary Miombo woodlands, where shrubs and small trees predominate due to past exploitation (Magalhães 2014). This land use change, from natural forest cover to plantations,may aff ect the evolution, cycle and spatiotemporal patterns of C storage and stocks in forest ecosystems. Estimation of C storage over time and space is indispensable for formulating climate change policies on sequestrating CO2(Chen et al.2019), and requires developing tools such as biomass models and biomass conversion and expansion factors (BCEF).

Biomass allocation patterns and tree allometry are widely aff ected by tree architecture (Coll et al. 2008; Trubat et al.2012). However, tree species may diff er greatly in architecture (Ketterings et al. 2001). Biomass allocation and tree allometry also vary with stand characteristics, e.g., density and composition (Zhang et al. 2015; Fang et al. 2018).Consequently, generic models (mixed-species models) are unlikely to yield accurate biomass estimates compared to species-specif ic ones (Vieilledent et al. 2012; Annighöfer et al. 2016; Goussanou et al. 2016); i.e., species-specif ic models are preferred over generic ones. Thus, when modelling biomass, species-specif ic Effects need to be incorporated in order to account for inter-species variability. One effi cient way of incorporating inter-subject variability is through mixed-Effects models.

To quantify the impact that planting exotic species on former secondary Miombo lands has on carbon sequestration, biomass models and estimates are required for both Miombo species and exotic species. Because the exotic species are predominantly species ofEucalyptus(e.g.,E.cloezianaF. Muell.) andPinus(e.g.,P. elliottiiEngelm., P.patulaSchltdl. & Cham.,P. taedaL.) and the Miombo species comprise mainlyBrachystegia spiciformisBenth. andJulbernardia globif lora(Benth.), biomass equations on these species are indispensable.

This research aimed to: (1) f it species-specif ic allometric biomass models and biomass conversion and expansion factors (BCEF) for exotic and indigenous species; and, (2) test the allometric universal scaling law between aboveground biomass and diameter at breast height (DBH).

Materials and methods

Experimental site

The study area is in the Machipanda locality in the central province of Manica, in the Inhamacarri Forest owned by Machipanda Agroforestry Centre of the Eduardo Mondlane University. The Forest is located between 32°37′30″ and 32°42′43″ E and 25°54′15″ and 25°56′40″ S, and is in hilly terrain with altitudes varying from 1400 to 1700 m a.s.l.Mean annual temperature is about 21 °C and mean annual precipitation is estimated at 1300 mm (Guedes et al. 2018).Soils are mainly deep, intensely weathered Ferralsols and slight to moderately weathered Cambisols with weak horizontal diff erentiation (Guedes et al. 2018).

The indigenous forests are small-sized trees ofB. spiciformis,J. globif lora, andUapaca kirkianaMüll. Arg. and the plantations are monocultures ofPinus(P. taeda, P. elliotti,and P. patula),Eucalyptus(E. cloeziana,E. grandisW. Hill, andE. camaldulensisDehnh.) and more recently,Araucariaspp. The plantations were established on former wet Miombo soils (Guedes et al. 2016).

Data acquisition

The target species with DBH ≥ 5 cm were the Miombo speciesB. spiciformisandJ. globif lora, and plantations ofE.cloeziana,P. taeda,P. elliotti, andP. patula(Table 1). A total of 120 trees, distributed among the species as shown in Table 1, were randomly selected, their diameters measured,and harvested.

Total heights (H) were recorded, and the trees divided into aboveground biomass (AGB) components, stem and crown. The stem was def ined as the length of the trunk from a predef ined stump height of 20 cm to a top diameter of 2.5 cm. The crown was the sum of branches, foliage, seeds,f lowers, and the remaining portion of the stem, from the 2.5 cm diameter height to the tip of the tree.

The stem was dived into f ive equal segments and the diameter measured at the midpoint. After fresh-weighting each segment, a disc sample was removed from the top, fresh weighted, oven-dried at 105 °C to constant mass, and subsequently re-weighed. The dry mass of the whole segment was then obtained by multiplying the ratio of oven dry to fresh mass of the disc by the fresh mass of the segment. The dry mass of the stem (stem biomass), was the sum of the dry masses of the constituent segments. The volume of the stem was computed using Hohenadl’s formula (Magalhães and Seifert 2015a).

For logistical reasons and to ensure the largest sample size, the foliage was not separated from the branches, as it is a time-demanding task. The crown was fresh weighed, a sample was collected, weighed in the f ield, and oven-dried in the laboratory. To ensure proportionality in sampling, the primary branches were divided in coarse (Ø ≥ 5 cm), and f ine (Ø < 5 cm), where Ø is the diameter of the branch at the insertion point on the stem. For each size class, a primary branch with mid diameter was selected and a 3-5 cm disc removed from the insertion point. A portion of the twigs,leaves, f lowers, and fruits of each primary branch was collected. The crown sample, therefore, consisted of the discs,twigs, leaves, f lowers, and fruit from the selected branches.The dry mass of the crown was obtained similarly to that for each stem segment. The total aboveground biomass (AGB)was the sum of the dry masses of the stem and crown.

CV (%)41.4 18.8 30.3 25.4 29.1 32.3 CV (%)60.7 61.1 98.8 SD 11.6 1.9 5.6 4.1 2.4 2.5 SD 877.4 174 21 83.5 7.1 14 CV (%) Mean Min Max 65 11.3 32 269.3 12.5 502.2 129.3 674.7 200.3 135.5 Height (m)12 43.2 12.5 10.3 20 6.9 281018.5 16.1 8.3 7.8 AGB (kg)504.4 24.9 507575.6 34.5 13.3 276.5 22.4 1383.5 359.6 130 136.6 306.3 130.9 147.8 44.4 23.6 93.4 25.2 42.7 53.1 CV (%) Mean Min Max 71.1 87.5 69 SD 9.6 2.8 9.3 5.6 6.5 7.1 8 SD 50.6 160.4 47.5 21.7 88.9 123.2 CV (%) Mean Min Max 8.7 56 155.6 22.1 42.2 8.7 17.3 11.4 42.2 5.8 28 5.6 34 Crown biomass (kg)CV (%) Mean Min Max 262.8 21.6 67.8 366.4 366.1 110.5 137.9 DBH (cm)0.9 41.4 6.5 22.1 21.7 129.9 22.1 15.2 15 31.5 10 54.3 31.4 72.1 80.1 42.8 27.7 44.3 28.6 38.3 46.3 176.4 59.1 77.5 SD 11.1 4.3 12.1 6.8 7.6 9.1 SD 14.5 222.2 21.1 1274.4 328.8 14860.3 1st and 2nd 472.9 18.2 4872.9 834 63.5 45.5 92.4 136.5 10.3 22.9 Mean Min Max 11.1 56.1 11.2 70.4 34.2 7.4 33 53.9 9.5 41.4 211.7 158.7 344.4 RCD (cm)13 Stem biomass (kg)Mean Min Max 9.3 105.2 224.4 4.8 Table 1 Overview and summary statistics of the observed data 15.5 27.4 23.6 19.9 19.5 24.5 58.7 67.7 Age (years) Rotation 1st and 2nd 25.9 2nd 1st 1st NA NA 2nd 1st 1st NA NA Number of trees (n)19, 22, 55 106017NA NA Age (years) Rotation 19, 22, 55 106017NA NA 42111413 Number of trees (n)42111413 Species E. cloeziana P. elliottii P. patula P. taeda B. spiciformis 2218 J. globifl ora Species E. cloeziana P. elliottii P. patula P. taeda B. spiciformis 2218 J. globifl ora N/A not applicable

Data analysis

Tree component biomass models were f itted using nonlinear regression, being preferred over linear ones because biomass is a nonlinear function of stem diameter and height (Schroeder et al. 1997; Ter-Mikaelian and Korzukhin 1997; Bolte et al. 2004; Salis et al. 2006). Power or allometric functions, as an extension of nonlinear functions, were preferred over other forms of nonlinear functions because growing plants maintain the proportions between diff erent parts, e.g., between tree biomass and predictive biometric variables such as DBH and tree height (Pilli et al. 2006). Allometric growth is observed when a constant ratio or proportion is maintained between the growth rates of diff erent parts of the plant (Enquist 2002; Opik and Rolfe 2005). This is observed between biomass and the easily measurable variables DBH and height(Zianis and Mencuccini 2004; Fehrmann and Kleinn 2006;Pilli et al. 2006). Biomass allometric functions are represented asy=bx k, whereyrepresents tree or component biomass,xan easily measurable tree variable,kis the ratio of growth rate betweenyandx,andbis the scaling coeff icient. The ratio of growth rate is the scaling exponent(Zianis and Mencuccini 2004; Fehrmann and Kleinn 2006;Packard and Boardman 2008). Because both the scaling coeffi cient and the scaling exponent vary with species(Pilli et al. 2006) as a result of varying architecture and wood density (Ketterings et al. 2001), species-specif ic allometric models; are preferred over general ones. Architecture inf luences biomass allocation and allometry (Coll et al. 2008; Trubat et al. 2012). Therefore, biomass models were f itted using nonlinear mixed-Effects (NLME) models to incorporate inter-species variability. The general form of NLME models is:

wherefis a nonlinear function of the parameter vectorφ ij,a composite parameter vector incorporating both f ixed and random Effects, and the predictor vectorx ij,Mis the number of species,n ithe number of trees within a species,Y ijthe response vector or tree component biomass vector for then itrees in theith species, andε ijthe vector of multivariate normally distributed errors in speciesi.φ ijis modelled as:

whereβis the vector of f ixed-Effects parameters,δ ithe vector of random-Effects parameters for speciesi,A ijandB ijare design matrices of known constants for combining the f ixed and random Effects of speciesi.

Biomass models were f itted using allometric equations,a specif ic form of nonlinear equations, expressed as:

Therefore, the general form of allometric mixed-Effects model is expressed as:

whereβ0is the f ixed scaling coeffi cient,δ0ithe random scaling coeffi cient for speciesi,β1the f ixed scaling exponent,δ1ithe random scaling exponent for speciesi, φ0ithe composite scaling coeffi cient (β0+ δ0i, f ixed + random scaling coeffi cient) for speciesi,φ1ithe composite scaling exponent(β1+δ1i, f ixed + random scaling exponent) for speciesi.

The relation between response variable, the tree component biomass, and the predictors DBH and height were described by the widely used allometric biomass functions(Zianis et al. 2005; Cienciala et al. 2006; Vejpustková et al.2015), as follows:

Additionally, a model form using the root collar diameter (RCD) only as a predictor was considered to allow the estimate of harvested biomass, as after harvesting the stump dimensions are still available.

Allometric models are often f itted to logarithmically transformed data (Overman et al. 1994; Bervian et al.2006; Cienciala et al. 2006; Blujdea et al. 2012; Makungwa et al. 2013; Paul et al. 2013a, b, 2019; Vahedi et al. 2014;Annighöfer et al. 2016; Goussanou et al. 2016; Chen et al.2017) to deal with heteroskedasticity, where the standard errors of a variable, over a specif ic time, are non-constant(Overman et al. 1994; Blujdea et al. 2012; Zapata-Cuartas et al. 2012; Vahedi et al. 2014; Goussanou et al. 2016).They facilitate model f itting by transforming the equation to a linear form (Overman et al. 1994; Blujdea et al. 2012;Zapata-Cuartas et al. 2012; Goussanou et al. 2016), allowing the use of linear least squares. In this study, logarithmic transformation of the data was avoided because the results of standard statistical tests performed on such data are often not relevant (Feng et al. 2014). Log-transformation leads to biased results (Packard and Boardman 2008). Traditional allometric method, which consists of linear f itting to logarithmically transformed data and back-transformation to power-law form, is not well suited for f itting statistical models to data expressed in the arithmetic scale (Packard 2013). Castro et al. ( 1996) maintained that modelling raw un-transformed data gives the best results.

To address within-species heteroskedasticity, the models in Eqs. 5- 8 were, instead of being log-transformed, f itted using weighted NLME models. This is justif ied because,quite often in regression, the error variance is functionally related to the predictors (Parresol 1999), i.e., the variability of the biomass increases with the predictors (Picard 2012).

The weight functions that describe the within-species heteroskedasticity structure were obtained by modelling the error structure of ordinary least squares (OLS), following the description by Parresol ( 1999, 2001). The squares of OLS residuals were f itted against the diff erent combination of the predictors and it was assumed that the squares are representative of the error variance (Parresol 2001). NLME models were f itted using the NLME package (Pinheiro et al.2019) of R software (R Core Team 2020).

Various authors have suggested that tree biomass scales against stem diameter with a universal scaling exponent of 8/3 (West et al. 1999; Enquist 2002; Pilli et al. 2006).However, several researchers have noted a lack of agreement between the scaling exponent in allometric equations and the universal scaling exponent (Chambers et al. 2001; Zianis and Mencuccini 2004; Li et al. 2005; Návar 2009). Other researchers have stressed that the universal scaling exponent is not acceptable, since the ratio of aboveground biomass to diameters in diff erent environmental conditions is not constant (Zianis and Mencuccini 2004; Niklas 2006), and because there is a large variability in allometry across species (Zapata-Cuartas et al. 2012 ). Therefore, to test the allometric universal scaling law, Eq. 5 was ref itted for all tree components with the scaling exponent set to 8/3. Predicted biomass values from Eq. 5 f itted without and with limitations on the scaling exponent and the observed biomass were compared using one-way ANOVA. Pairwise comparisons among biomass means were tested using Tukey HSD test.

When f itting the models, parameters, either f ixed or random, with estimates not signif icantly diff erent from zero at α = 0.05 were removed, and the reduced model ref itted. This procedure was continued until only parameters with statistically signif icant estimates remained.

Tree component BCEFs were computed as the ratio of tree component biomass and stem volume (Magalhães and Mate 2018). A three-way ANOVA was carried out to test for the Effects of species, DBH and total height on BCEF. Tukey HSD test was used to f ind species-level BCEFs statistically diff erent from each other.

Communality analysis was carried out to quantify the variance that was unique to each predictor and the variance that was common to groups of predictors, thereby identifying which predictor accounted the most to the variability of BCEF. Commonality analysis was performed using “yhat”package (Nimon et al. 2015). The dependence of BCEF on DBH and height was analysed by testing the signif icance of the Pearson´s correlation coeffi cient.

All statistical analyses were performed at a 5% signif icance level.

Model evaluation and validation

Predictive accuracy determined which model(s) described the relationship between component biomass and the most used dendrometric predictors better, based on the following g oodnessoffitstatistics:Akaike´s Information Criterion,AIC,(Akaike1973),meanresidual(vonGadow and Hui 1999), modelprecision V (Calama and Montero 2004; Correia et al. 2010a), Furnival´s index of f it, FI (Furnival 1961),and the root mean square error, RMSE (von Gadow and Hui 1999), Eqs. 9- 13, respectively:

whereL iis the maximum likelihood of theith model, Pithe number of parameters of theith model,Y iobserved biomass,predicted biomass of theith model,ε ijresidual from the biomass of thejth tree of theith model,f´(Y)is the f irst derivative of the transformed response variable, and MSEithe mean square error of theith model. Square brackets indicate the geometric mean.

For ease of comparison between models,V, and RMSE were expressed as relative values, a percentage of observed biomass Y, which is more revealing. Model precision (V)was expressed as the standard error of the residuals.

The coeffi cient of determination (R 2 ) was not used to evaluate the performance of the models because it is inappropriate for demonstrating the performance or validity of nonlinear models (Spiess and Neumeyer 2010; Magalhães and Mate 2018). This is because the regression sum-ofsquares and the residual sum-of-squares do not total the sum-of-squares as in linear least squares, and thus R 2 is no longer between 0 and 100% (Magalhães and Mate 2018).

To evaluate the predictive ability, the models were validated using an independent dataset. The following statistics were used: model effi ciency or EF, (Soares et al. 1995; Vanclay and Skovsgaard 1997) and Error (Calama and Montero 2004), Eqs. 14 and 15. Additionally, observed and predicted biomasses were compared using the Wilcoxon signed rank test.

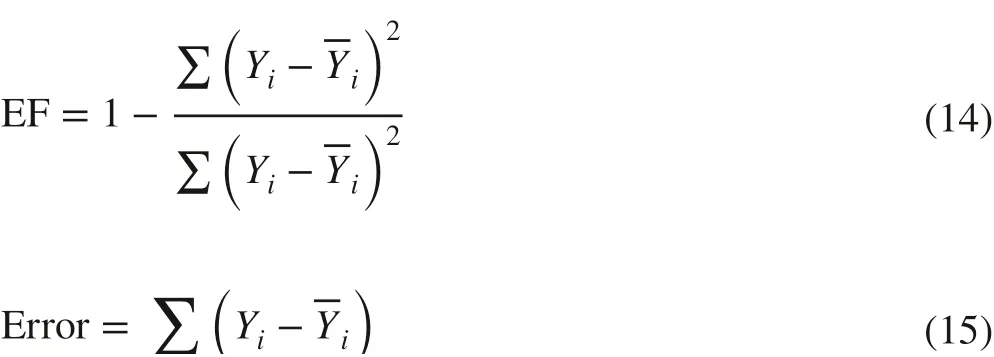
EF was expressed as a percentage. The ideal values of EF and Error are 100% and 0%, respectively, indicating perfect predictive ability. Therefore, models with the largest EF,the smallest Error, and no signif icant diff erence between observed and predicted biomass, as judged by the Wilcoxon test, were considered the best.

The independent dataset used for validation consisted of data from 81 trees: 12B. spiciformis(DBH 5.1-34.0 cm),8J. globifl ora(DBH 5.0-29.3 cm), 6E. cloeziana(DBH 23.0-39.0 cm), 28P. taeda(DBH 9.5-38.5 cm), 10P. elliotti(DBH 9.8-25.5 cm), and 17P. patula(DBH 14.5-28.5 cm).Of these sampled trees, 59 were collected in 2017 (Guedes et al. 2018) and the remaining collected between 2014 and 2018 for various unpublished research.

Results

Measured data

Component biomass plotted against DBH, stratif ied by species, strongly followed a power relationship for all components (Fig. 1). Tree species revealed a diff ering set of trees,especially for crown biomass. The power trend was strong for stems and AGB but the scatter was larger for crowns,especially for larger DBH trees. The ratio of stem biomass to AGB was larger for exotic species than for indigenous species, and amounted to 94%, 81%, 77%, and 71% forE.cloeziana, P. patula, P. taeda, and P. elliotti,respectively(Fig. 2). For the Miombo species, the largest ratio was crown biomass to AGB, and amounted to 55% and 54% forB. spiciformisandJ. globif lora, respectively (Fig. 2).

Fig. 1 Biomass plotted against diameter at breast height

Fig. 2 Component biomass partitioning for diff erent exotic and indigenous species

The share of component biomass on total aboveground biomass showed a species-specif ic pattern (Fig. 3). For all exotic species except forPinus patula,the percentage of stem and crown biomass was stable over the DBH range.The percentage of stem biomass ofP. patulaincreased slightly with diameter and a slight decrease was found for crown biomass. For the Miombo species, while the percentage of stem biomass decreased steeply with DBH, there was a steep increase for the percentage of crown biomass with DBH. ForB. spiciformis, the portion of stem biomass to AGB decreased with DBH from approximately 90% to 30%and that of the crown increased from 14 to 73%. Similar results were observed forJ. globif lora, with the percentage of stem biomass decreasing with DBH from 87 to 8% and the crown increasing from 13 to 92%.

Biomass allometry

Species-specif ic allometric biomass models with DBH,RCD (root collar diameter), and height (H) as predictors and component biomass as response variables were constructed. The weight functions and the random scaling coeffi cients and exponents of the models were inf luenced by species-specif ic factors and by biomass components.All f ixed scaling exponents and f ixed and random scaling coeffi cients were signif icant at α = 0.05 (Tables 2, 3, 4 and 5). However, the random scaling exponents were signif icant only for crown biomass models (Tables 2, 3, 4 and 5). All biomass allometric models had an acceptable predictive accuracy and ability (Table 6). However, stem and AGB allometric models f itted the data better than crownmodels as indicated by the AIC, V, E, FI, and RMSE values (Table 6).

Fig. 3 Pattern of biomass components on AGB as governed by diameter at breast height

Table 2 Parameter estimates of the models for stem biomass

Using only DBH as a predictor, the models estimated tree component biomass with a satisfactory predictive accuracy, i.e., model precision (V) < 2% and mean residual (E)not statistically diff erent from zero, and predictive ability,model effi ciency (EF) > 72% and Wilcoxon test revealing that observed and predicted biomass were statistically identical. Adding height as an incorporated variable (D 2 H) or as a second variable improved the predictive accuracy and ability, however better prediction was observed when height was added as a second variable (Eq. 6,Y=φ0i×Dφ1i×Hφ2i+ε).Adding height as an incorporated variable (D 2 H), AIC,model precision V, and the root mean square error, RMSE,decreased up to 5%, 23%, and 26%, respectively, and the EF increased up to 15%. However, adding height as a second variable, the AIC, V, and RMSE decreased up to 10%, 28%,and 50%, respectively, and EF increased up to 28%. The allometric biomass model including height as the second predictor (Eq. 6) was the best for all components.

Satisfactory predictive accuracy and predictive ability were also attained for the models using only root collar diameter (RCD), however the models were not better as those with only DBH as a predictor (Table 6). The models fitted using the universal scaling exponent (D 8/3 )were better than the RCD models and fitted the data similarly as the DBH models. Figure 4 shows clearly that the measured biomass, the predicted biomass from Eq. 5, and the predicted biomass using the universal scaling exponent did not differ statistically.

Using the interactive D 2 H as a predictor, an isometric scaling (b1= 1) was obtained for all tree components,implying that, for the DBH range considered in this study,the ratio of biomass and D 2 H was constant. A positive allometry was found when DBH or RCD were used as the sole predictor. A f ixed scaling exponent (b1) of ≈ 3(range: 2.89-3.07) was found when RCD was used as the predictor. Using only DBH as a predictor, the f ixed scaling exponent (b1) ranged from 2.60 to 2.89. These f ixed scaling exponents, obtained when biomass is scaled against DBH only, were not statistically diff erent to the universal scaling exponent (8/3) proposed by West et al. ( 1999).

Crown models using only DBH as a predictor for the Miombo species had larger scaling exponents (up to 25%)than those for exotic species. The larger values for the indigenous species imply that, per unit of DBH growth,the increment of crown biomass is larger, up to 25%, compared with exotic species. Note that, for stem biomass and AGB models, the random scaling exponents were not statistically diff erent from zero, thus the composite scaling exponents were equal to the f ixed ones, denoting that a unit of DBH increase resulted in similar stem and aboveground biomass increment for all species.

Table 3 Parameter estimates of the models for crown biomass

Biomass conversion and expansion factors (BCEF)

Biomass conversion and expansion factors (BCEF) are widely used to convert timber volume of forest inventories to tree biomass, and are calculated as the ratio of component biomass to stem volume. Aboveground biomass ofB.spiciformisandJ. globif lorawere approximately 157% and 139% of the stem volume (Table 7), respectively; however,the AGB of the exotic species were only up to 69% of stem volume. This suggests that Miombo species store more than double the aboveground biomass per stem volume, i.e.,the BCEF are more than double that of the exotic species.Miombo species store up to 13 times more biomass in the crown per stem volume than the introduced species.

The three-way ANOVA revealed that, for all three components, stem, crown, and shoot system, the species was a signif icant source of variation of the BCEF (P value= 0.0000).In addition to species, DBH and height also had signif icant Effects on crown BCEF; height was also a signif icant source of aboveground BCEF variation. Tukey HSD test showed that BCEF values of the two Miombo species were statistically superior to those of all introduced species (Table 7).

From the commonality analysis, the majority (60-99%)of the regression Effect was explained by variance that was unique to a species, i.e., species uniquely accounted for up to 99% of the regression Effect. Tree species accounted for 59.5%, 62.5%, and 99% of the regression Effect of crown,aboveground, and stem BCEF, respectively.

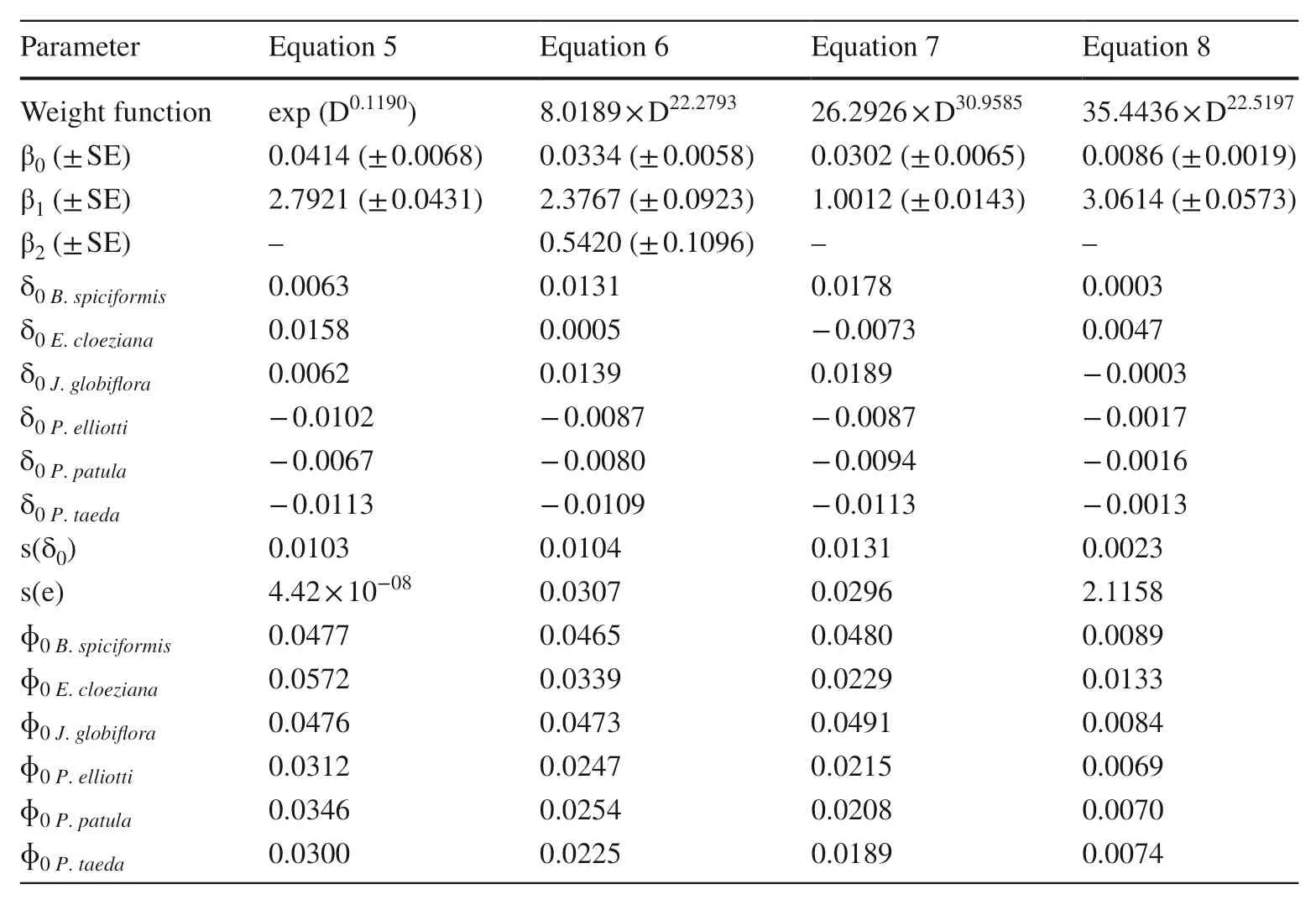
Table 4 Parameter estimates of the models for aboveground biomass

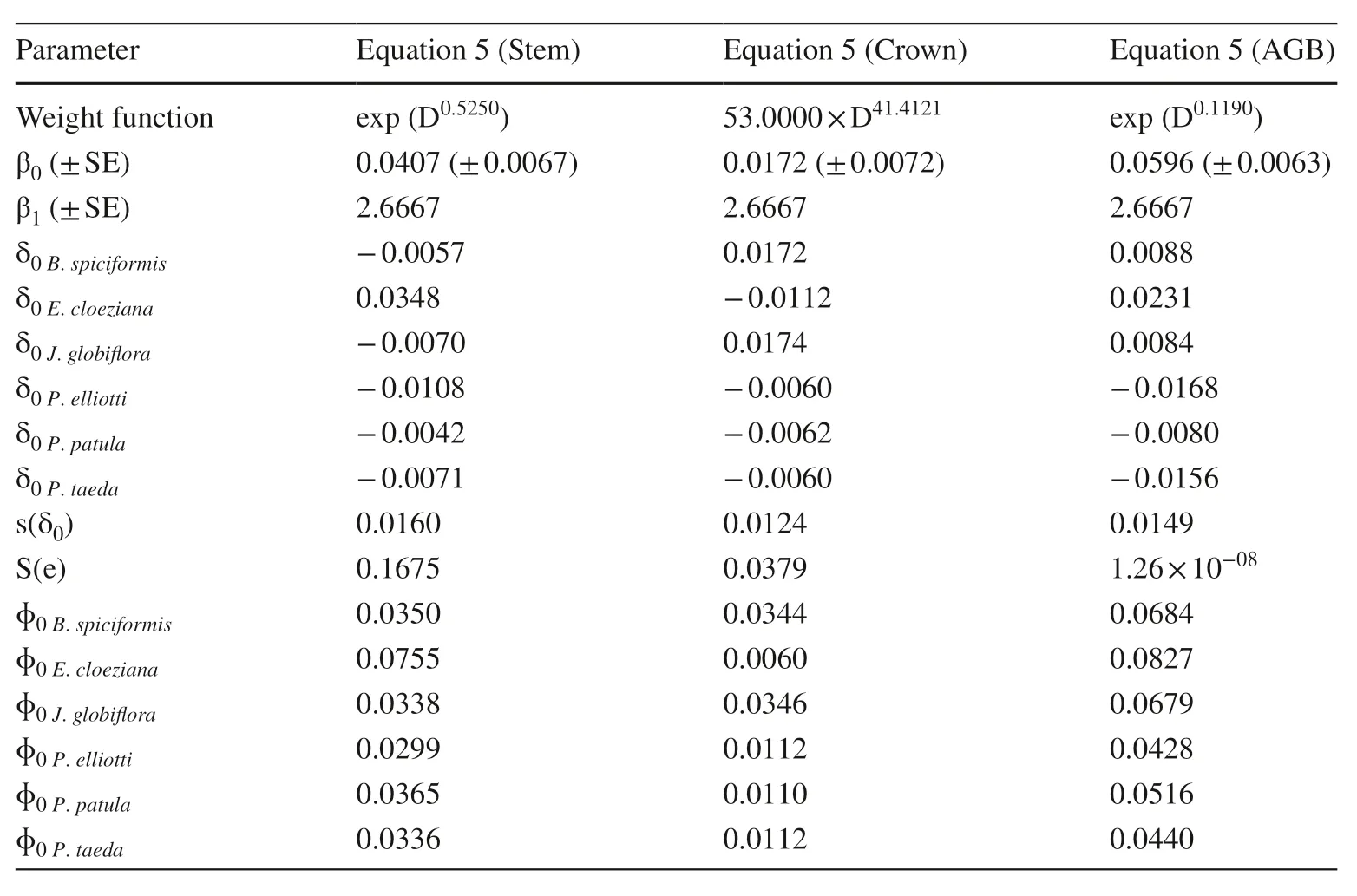
Table 5 Parameter estimates of Eq. 5 f itted using universal scaling exponent

Tree component BCEF of all exotic or introduced species, and stem and aboveground BCEF of Miombo species were not linearly correlated to DBH nor to height (P value> 0.2). Crown BCEF of Miombo species was positively dependent on both DBH and height (Fig. 5), and Pearson´s correlation coeffi cients between crown BCEF and DBH and height were 0.55 (P value= 0.0002), and 0.33 (P value= 0.0349), respectively.

Discussion

Biomass allocation patterns

Studies on biomass allocation patterns into diff erent tree components are of considerable interest in forest carbon monitoring and dynamics (Fournier et al. 2003; Pajtík et al.2008; Magalhães and Seifert 2015b). For example, with theMiombo woodlands, while the stem or bole is used in the forest industry and thus the C remains stored for some time,the branches are either left in the forest or collected and used as f irewood by local communities. In either case, the stored carbon is released to the atmosphere by decomposition or burning.

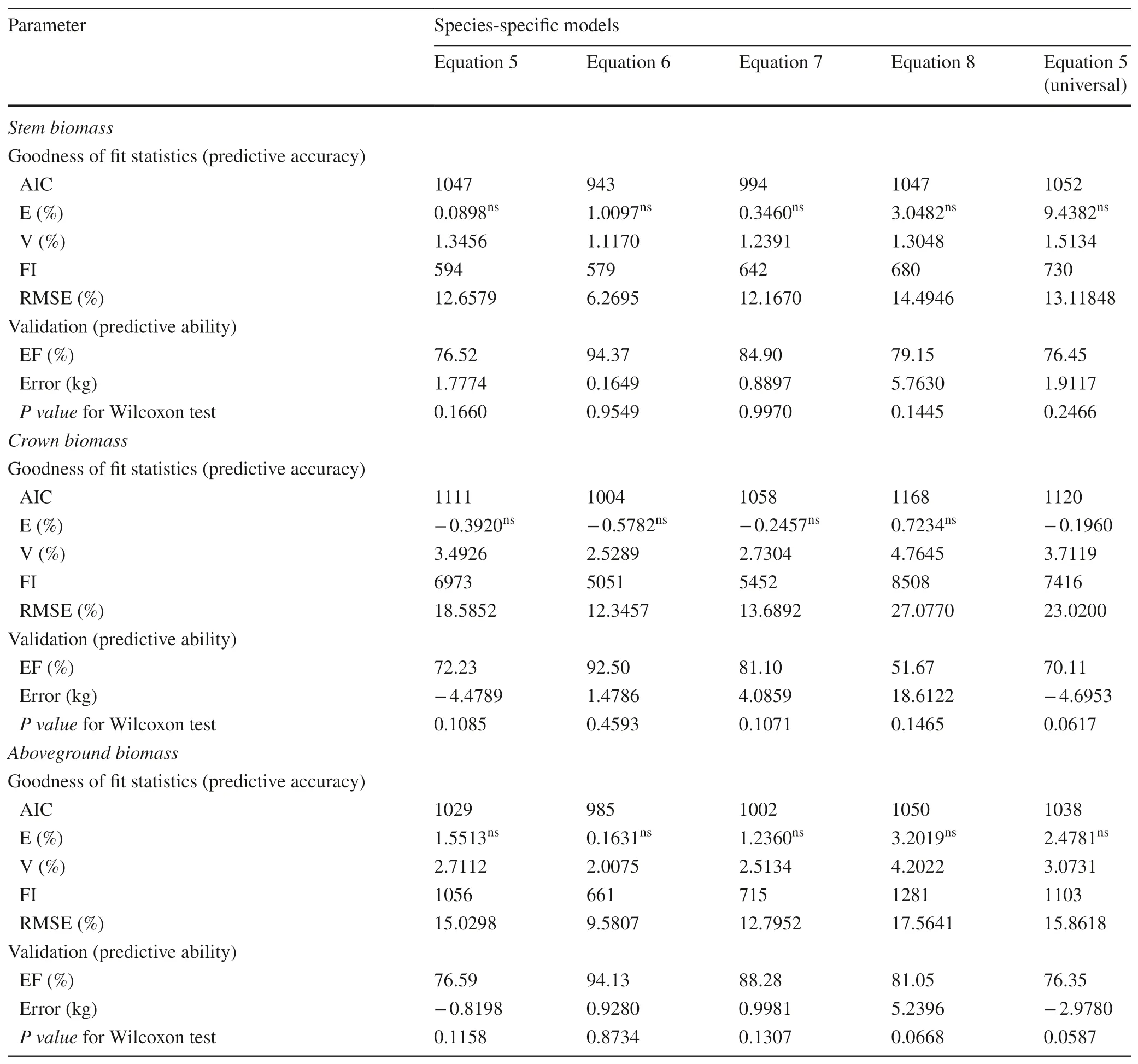
Table 6 Predictive accuracy and ability of the f itted models

The biomass allocation patterns of the exotic species in this study is in agreement with a number of studies (Cienciala et al. 2006; Correia et al. 2010a, b; Xiang et al. 2011;Vargas-Larreta et al. 2017) forPineandEucalyptusspecies; as trees grow larger, the proportion of aboveground biomass allocated to the stem increases and that allocated to the crown decreases, and/or the majority of the AGB is allocated to the stem. However, this pattern of allocation was not supported by the two Miombo species as most of the AGB was allocated to the crown, and the proportion increased with increasing tree size. An increase proportion of branch biomass, and thus crown biomass, has been reported by Pajtík et al. ( 2008) for Norway spruce (Picea abies(L.) H. Karst.). The proportion of AGB allocated to the stem for the Miombo species in this study, 45% and 46%forB. spiciformisandJ. globifl ora, respectively, is lower than that reported by Henry et al. ( 2010) for tropical rain forests of Africa (69%), by Peltier et al. ( 2007) for tropical dry forests (70%) and by Henry et al. ( 2009) for tropical agroforestry systems in Kenya (62%).

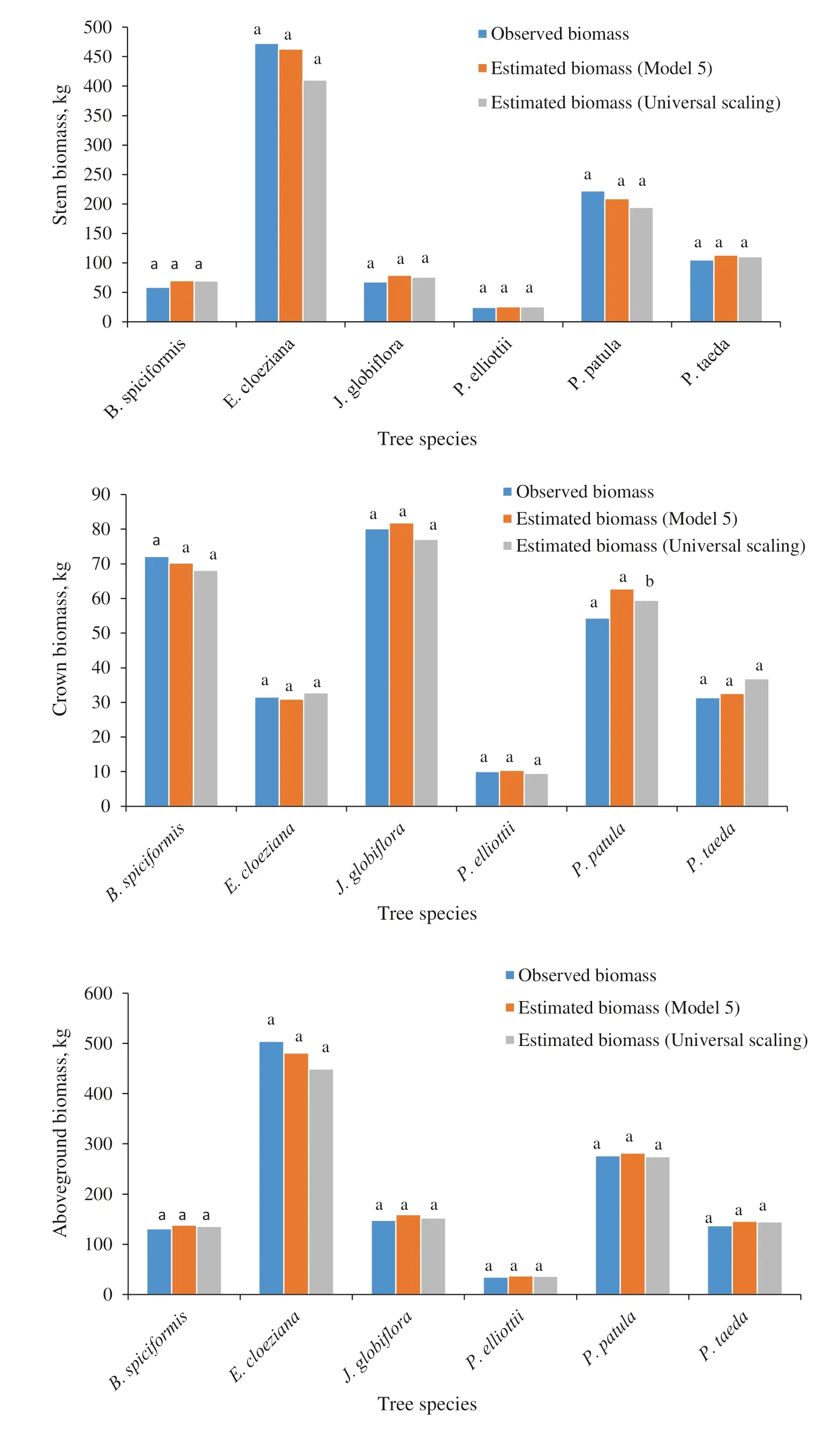
Fig. 4 Tukey HSD test results showing the similarities between observed biomass,predicted biomass by Eq. 5, and predicted biomass using the universal scaling exponent

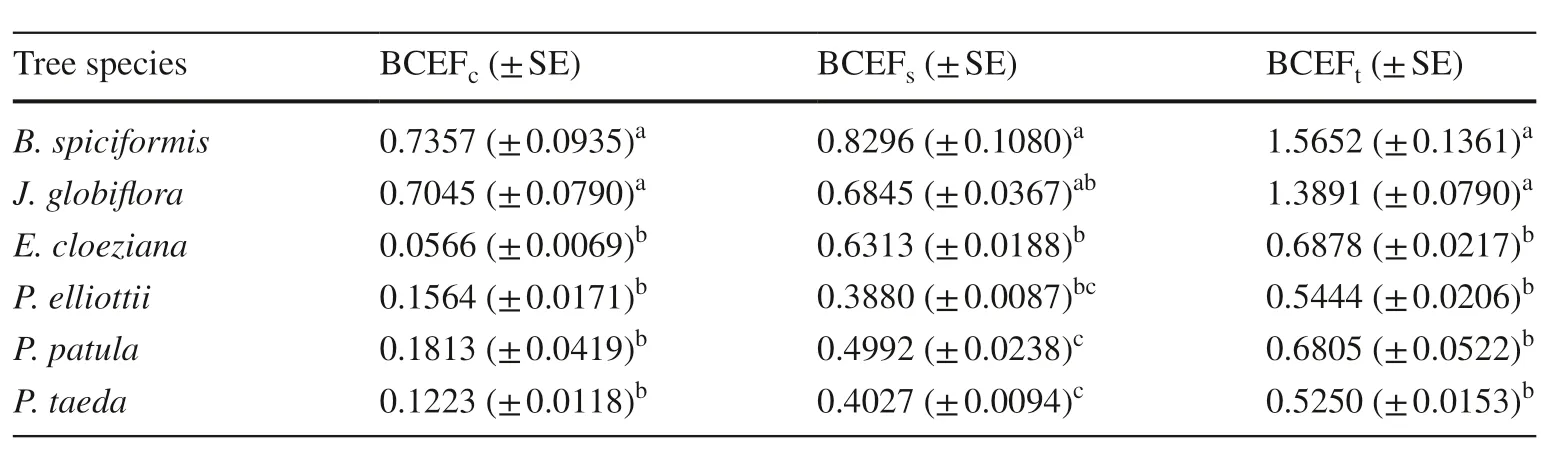
Table 7 Average (± SE)BCEFs (Mg m− 3 ) per species and per tree component

The diff erent biomass allocation patterns of indigenous and exotic species could be a result of diff erences in stand density. The Miombo forest is composed of small trees(Table 1) and no more than 200 trees per hectare, while the plantations have upwards of 1000 trees per hectare.Xiang et al. ( 2011) maintained that stand density enhances the proportion of stem biomass but decreases biomass of branches. As a consequence of competition for light, exotic species have small branches and smaller quantities of leaves,resulting in smaller crowns than indigenous species which do not face limitations in light resources and growing space.Crown size has been reported to decrease with competition(van Laar and Akça 2007) as a result of natural pruning as a consequence of inter-tree competition for light and growing space and self-shading and shading by neighbouring trees.

Biomass allometry

Miombo species are the most important trees of southern Africa and of Mozambique (Ribeiro et al. 2015; Aquino et al. 2018), andEucalyptusandPinusspecies the most important reforestation species, planted mainly for commercial purposes (Blid 2014). Therefore, the accurate estimation of biomass of the Miombo species and theEucalyptusandPinusplantations is essential. The species-specif ic allometric models developed here predict biomass accurately for the exotic and indigenous species across the range of DBHs used to develop the models (Table 1) and have good applicability as tested using the independent samples. Nevertheless, it is not advisable to extrapolate beyond the data range as the results may be biased.

Crown models for the Miombo species had larger composite scaling exponents (up to 25%) compared with those of the exotics, and composite scaling coeffi cients were constant for all species as a result of insignif icant random scaling coeffi cients. As a result, the Miombo species had high predicted biomass for a given diameter and height compared with the exotic species. This is consistent with the f inding that: (1) Miombo species store more biomass per stem volume than exotic species; (2) Miombo species allocate more biomass to crowns than to stems as compared to exotic species (Fig. 2); and, (3) per unit of DBH growth, the increment of crown biomass of Miombo is larger than that of exotic species. However, although Miombo species had larger increments of crown biomass per unit stem diameter growth and stored larger amounts of biomass per stem volume than the exotic species, due to their rapid growth, larger stem diameters and heights (on average), and stand density, the plantations store more biomass per tree and per unit area.

For all models, AGB and stem biomass had higher predictabilities than crown biomass. This is in agreement with Jagodziński et al. ( 2018a, b). Branch and crown biomass components are diffi cult to estimate with the same accuracy as stem biomass or total aboveground biomass (Vargas-Larreta et al. 2017). The high predictability of stem biomass and AGB models is attributed to the high correlation between these component biomasses and DBH (Fig. 1).

Diameter at breast height was the main predictor for estimating tree biomass components for all species, indigenous and exotics. For all components, the inclusion of height signif icantly improved the predictability of aboveground biomass and stem and crown biomass. Height as a second predictor substantially improved model precision (V) of stem biomass, AGB and crown biomass by 17%, 26%, and 28%,respectively, and model effi ciency (EF) was improved by 23%, 23%, and 28%, respectively. The inclusion of height led to a substantial increase in predictive accuracy and ability.This is consistent with the f indings by Pajtík et al. ( 2008),Xiang et al. ( 2011) and Vargas-Larreta et al. ( 2017). However, other researchers (Johansson 1999; Porté et al. 2002;Jenkins et al. 2003) reported that the inclusion of height does not lead to a signif icant increase in predictive ability.

Fig. 5 Component BCEFs plotted against diameter at breast height and height

Height is not directly measured in forest inventories and it is thus more susceptible to measuring error than DBH(Loetsch et al. 1973; Machado and Figueiredo Filho 2006;Sanquetta et al. 2006) and its measurement is not standardized (Sileshi 2014). Therefore, although with better predictability, models using height (Eqs. 6, 7) will lead to biased results because of inherent measurement errors of tree height. The inclusion of height in Eq. 4, either as a combined variable D 2 H (Eq. 7) or as a second predictor(Eq. 6), will introduce two sources of errors over and above those expected in Eq. 4 (Sileshi 2014): (1) errors due to measurement of height; and, (2) errors due to the estimation of model parameters. Moreover, 1-predictor biomass models, (DBH only models), are easier and faster to use and less expensive than 2-predictors models since the latter require height measurements which are expensive and time-consuming.

In biomass modelling, height is included in the model,either as a combined variable D 2 H (Eq. 7) or as a second variable, in addition to DBH (Eq. 6) (Zianis et al. 2005;Cienciala et al. 2006; Vejpustková et al. 2015). In this study,better prediction and accuracy were obtained when height was added as a second variable (Eq. 6). This contradicts Carvalho and Parresol ( 2003) and Bi et al. ( 2004) who obtained better estimates for the model with a combined predictor D 2 H. However, our results are consistent with Vahedi et al.( 2014) and Vejpustková et al. ( 2015).

Biomass conversion and expansion factors

Larger BCEF values were found for Miombo species and lower ones for the plantation species. Slow-growing species such asB. spiciformisandJ. globifl orahave high wood density, whereas fast-growing species (e.g.,EucalyptusandPinusspecies) have low densities (Ouédraogo et al.2013; Yeboah et al. 2014; Ramananantoandro et al. 2016).This explains why slow-growing Miombo species (Grundy 1995; Elifuraha et al. 2008; Chiteculo and Surovy 2018) had higher biomass conversion and expansion factors compared to exotic species as these factors are directly proportional to wood density (Pajtík et al. 2008; Schepaschenko et al. 2018).In other words, BCEF = BEF ×ρ, where BEF and ρ are biomass expansion factors and wood density, respectively.

BCEFs have been reported to be reversely dependent on DBH and height (Brown et al. 1989; Lehtonen et al. 2004;Dutca et al. 2010; Sanquetta et al. 2011; Magalhães and Seifert 2015a) or to be independent of tree size (Marková and Pokorný 2011; Magalhães and Seifert 2015a). In this study, BCEF values of exotic species were not dependent on size; only crown BCEF of Miombo species were dependent on DBH and height. This is because the proportion of crown biomass on AGB increased with tree size, whereas that of stem biomass decreased (Fig. 3), resulting in BEF,and consequently BCEF, to increase with increasing tree size. At the same time, the stability of the biomass conversion and expansion factors of exotic species over tree size is also related to the stability of the proportions of crown and stem biomass on AGB over tree size (Fig. 3).

Dutca et al. ( 2010) maintained that the reverse relationship between BEF and tree size is a result of an inverse relationship between wood density and size. This suggests that the direct dependence of crown BCEF of Miombo species to tree size may be due to the direct relationship between branch wood density and size. Increasing wood density with age and tree size has been reported by various researchers(Pajtík et al. 2008; Nock et al. 2009; Henry et al. 2010; Deng et al. 2014). However, there are also studies showing that wood density does not vary with stem diameter (Ramananantoandro et al. 2016; Fajardo 2018), whereas others have reported that wood density decreases with tree age and size(Pajtík et al. 2008; Liepiņš et al. 2017). This pattern of variability in wood density explains the variability of patterns of BCEF with tree size (Fig. 3).

Stem, crown, and aboveground BCEF values ofB. spiciformisandJ. globif loraare larger than those observed by Magalhães and Mate ( 2018) for other Miombo species,Umbila (Pterocarpus angolensisDC.) and Chanfuta (AfzeliaquanzensisWelw.) except for Panga-panga (Millettia stuhlmanniiTaub.), and are also larger for other Mozambican indigenous species such as Mecrusse (Androstachys johnsoniiPrain) (Magalhães and Seifert 2015a) and Mopane(Colophospermum mopane(Kirk ex Banth.) Kirk ex J.Leonard) (Magalhães and Mate 2018). It was assumed that the diff erences in BCEF are attributed to the diff erences in climate, soil conditions, altitude, and species.

The majority of variation of the biomass conversion and expansion factors was attributed uniquely to species rather than to stem diameter and height, and this is consistent with Luo et al. ( 2014) who found that BCEF exhibited remarkable variation across forest types.

Conclusions

This study provided species-species biomass allometric models and biomass conversion and expansion factors for the Miombo speciesB. spiciformisandJ. globif loraand for exotic species ofEucalyptus cloeziana, Pinus elliotti, Pinus patula,andPinus taedagrowing in highlands of Manica province, Mozambique. The allometric biomass models, for all tree components, had an acceptable predictive accuracy and ability. The highest predictive accuracy and ability was found with models with tree height as a second variable(Y=φ0i×Dφ1i×Hφ2i+ε) . The Miombo species had larger increments of crown biomass per unit of stem diameter as seen by their larger scaling exponents. Similarly, they stored larger amounts of biomass per stem volume unit, i.e., their biomass conversion and expansion factors were up to 13-fold larger than those of the exotic species. The majority of the variation of these factors (up to 99%) was attributed uniquely to species rather than to diameter or height. Although with relatively lower, yet acceptable predictive accuracy and ability, the model f itted under the constraint of the allometric universal scaling law (Y=φ 0i×D 8/3+ε) showed that the universal exponent (8/3) was data acceptable for both indigenous and exotic tree species.

Acknowledgements Thanks are addressed to the f ield team (João Paulino from the Forest Harvesting Division, Romano Guiamba from the Soil Laboratory) and to the anonymous reviewers of the manuscript. Thanks are also extended to the staff of the Centro Agrof lorestal de Machipanda, Prof. Ernesto Uetimane and Mr Alfredo, who provided accommodation, transportation and other facilities for data collection.

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creat iveco mmons.org/licen ses/by/4.0/.

Publisher’s NoteSpringer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affi liations.