专家型数学教师的研究与展望——李业平教授访谈录
2021-04-30沈中宇刘思璐邹佳晨
沈中宇,刘思璐,邹佳晨
专家型数学教师的研究与展望——李业平教授访谈录
沈中宇1,刘思璐2,邹佳晨2
(1.华东师范大学 数学科学学院,上海 200241;2.华东师范大学 教师教育学院,上海 200062)
专家型数学教师的研究是教育研究的重要课题,通过对美国德克萨斯A&M大学李业平教授的访谈,探讨了专家型教师的研究历程和专家型数学教师的当代研究,并展望了未来的专家型数学教师研究.李教授认为:心理学研究是专家型教师研究中重要的研究背景;当代专家型数学教师的研究主题包括数学教学中专家知能的测评与发展等方面;在新时代教育改革的背景下,专家型数学教师的研究要面向未来,适应时代发展的需要.李教授建议:未来可以从专家型教师的数学学科素养、STEM视角下的专家知能、专家型数学教师的分类、数学教学专家知能的发展途径以及不同文化背景下的数学教学专家知能等角度对专家型数学教师开展研究.
专家型数学教师;专家知能;发展途径;国际比较
1 问题提出
数学教师的专业素养直接关系到学生的数学成就,随着教育改革的深入发展,培养和造就更多的专家型教师,是教育实践的迫切需要,也是教育研究的重要课题.20世纪70年代,国外开始出现专家型教师的研究,其后由于引入了认知心理学中对专家知能(expertise)的研究方法,专家型教师的研究开始在教育领域兴起.所谓专家知能是指专家有别于新手的知识、技能与性格等.中国专家型教师的相关研究出现较晚,起于20世纪90年代对教师成长规律的探讨[1].目前,中国正在进行新一轮教师教育综合改革,《中共中央国务院关于全面深化新时代教师队伍建设改革的意见》指出:“到2035年,教师综合素质、专业化水平和创新能力大幅提升,培养造就数以百万计的骨干教师、数以十万计的卓越教师、数以万计的教育家型教师.”[2]数学教师是中国教师队伍的重要组成部分,专家型数学教师的理论是数学教师成长与实践的指南.新时代,如何把握专家型数学教师研究的“风向标”,已成为数学教育关注的核心.
李业平教授是现任国际重要教育研究杂志《国际STEM教育杂志》()和《STEM教育研究杂志》()主编、国内《数学教育学报》编委会成员.李教授熟悉中美两国国情,曾先后主编《数学教学中的专家知能:国际的视角》()、《中国人如何获取和提升面向教学的数学知识》()等书,对专家型数学教师的专业发展有着深刻而独到的见解.2019年7月,正值李业平教授(下文简称“李”)在上海学术访问之际,研究者(下文简称“研”)就“专家型数学教师研究”这一主题,对其进行了约180分钟的访谈.李教授围绕专家型教师的研究历程、专家型数学教师的当代研究内容以及研究趋势等,详尽而深入地发表了自己的看法,这些观点对国内专家型数学教师的研究有着重要的参考价值.
2 访谈内容
2.1 从绝对专家到相对专家:心理学中专家知能研究方法演进
研:李老师您好,非常荣幸能够对您作专访.近年来,专家型数学教师研究是数学教育研究的一个热点话题[3–10],您认为专家型教师的研究经历了怎么样的历程?
李:专家型教师的研究在教育领域的研究历史很短,但在心理学的领域已有一百多年历史.相关的心理学文献里记载了一些有关专家知能的研究.
在研究历程方面,心理学家对专家知能的研究方法经历了从“绝对的方法”(absolute approach)到“相对的方法”(relative approach)再到“信息处理方法”(information- processing approach)的过程.
研:您能具体描述一下各阶段的研究方法吗?
李:早期心理学家只研究一般的心理过程,他们研究专家知能的方法被称为“绝对的方法”,即找绝对的专家,寻觅奇才.当时研究方法较少,主要靠观察如爱因斯坦这种奇才的外在表现(如身体特征,脑部结构等)与别人有哪些不同.后来出现了IQ测验,但其本身也存在争议.
几十年以后,心理学家逐渐有了新的方法叫做“相对的方法”,即观察专家和新手在相同的问题上,有什么不同的表现特征.举个例子,某位教授在他的领域内是专家,新进的大学生在该领域相对而言就是新手.
直到20世纪60年代到80年代初,随着计算机的引入,心理学家开始在研究专家的过程中采用“信息处理方法”.为了解人的内部心理操作机制,心理学家让人出声解答一个特定问题,并记录其结果,再基于解题过程的文本分析来编程,让计算机运行解同样的问题,发现计算机的结果和人的结果在很多情况下一致.这样就通过实证研究将计算机信息处理的系统与人脑处理信息的模型相联系,由此产生了“长时记忆”和“短时记忆”的概念.人的短时记忆(对应计算机的内存)有限,实验研究发现人的短时记忆容量为7±2个不相关字符;而人的长时记忆(对应计算机的硬盘)理论上是无限的,只不过大多数人没有充分利用长时记忆的记忆库.
研:您觉得以上研究方法的演进对专家研究有何重要意义?
李:对于专家本质的研究很重要.以往认为专家是天生的,只研究绝对的专家.后来承认有相对的专家,因此每个人都可能成为专家.
2.2 从解决策略到信息组织:心理学中专家知能研究内容扩展
研:在研究方法的嬗变过程中,所使用的问题具体发生了什么样的变化?又有哪些发现?
李:心理学家在其研究中所使用的问题,经历了从知识简洁(knowledge-lean)型问题到知识丰富(knowledge-rich)型问题的过程.
从研究中所使用的问题角度,早期的心理学家在其实验中所采用的问题是知识简洁型问题,以游戏为主,如汉诺塔问题,该问题涉及的知识较少,因此心理学家早期研究的是这类问题的解决策略.
后来,实验的问题慢慢转为知识丰富型问题,比如数学或物理题.结果发现人脑中的知识结构对问题的解决很重要.比如国际象棋大师下棋经常赢,一般人可能认为是由于记忆能力比普通人强.而心理学家实施了一个国际象棋大师和新手在棋盘复原方面的比较实验,结果发现:他们对于无序的棋盘,复原程度差不多;而对于实战情况的棋盘,前者比后者复原的程度好得多.其原因为前者的大脑对实战的棋盘有信息点[11].
心理学家从以上实验中发现,专家和新手之间的差异不在于一般记忆力,而是大脑中的组块信息(chunk informa- tion).这就说明人学习的过程不是单纯吸取信息的过程,而是不断重组和掌握这些信息的过程,当信息整合以后,人的大脑中会形成组块信息.当新手成为专家以后,他的大脑中会具有大量结构良好的组块信息.因此,心理学家就提出了认知结构理论.接着,心理学家通过实验来估计作为一个专家具有的组块信息数量,以及形成这些组块信息所需要的时间,最终估计的时间为10年.
除了国际象棋大师之外,心理学家开始研究更具学术性的学科领域(如物理、数学)的专家,研究表明,他们解题的过程不纯粹是结构化提取信息和使用信息的过程,也包括对问题表征的过程,这说明专家看问题的眼光和新手是不同的[12].
心理学的研究表明,通过个体的刻意练习[13]、团队协作[14]等手段可以发展专家知能.对于教师而言,不是所有的教师经过一定时间、经验积累都能成为专家型教师.这涉及到常规专家(routine expert)和适应性专家(adaptive expert)[15]两个概念.有些教师不会迁移,经过一定时间也只是教书匠,也就是常规专家;有些教师会反思,会贯穿不同的情境,经过一定时间就发展成教学专家,也就是适应性专家.
研:您觉得以上研究内容的扩展对专家研究有什么重要意义?
李:对于专家发展的研究比较关键.以往认为专家在问题解决的策略上表现出色,后来认识到专家在信息组织方面出类拔萃.在了解专家的本质以后,在心理学的基础上,可以争取发现一些使得新手成为专家的较快捷的途径.
2.3 关注整体与重视划分:数学教学专家知能测评研究的两种取向
研:进入21世纪以来,国际上专家型数学教师的研究逐渐增多,据您了解,当代数学教育研究者对专家型数学教师开展过哪些研究?
李:教学中专家知能的研究情况和心理学中专家知能的研究是不太一样的,早期几乎没有人研究过教学方面的专家知能.20世纪80年代,美国匹兹堡大学的莱因哈特(G. Leinhardt)等人用“信息处理方法”研究过课堂教学的专家知能[16],但是未涉及学生层面.进入21世纪后,很多数学教育研究者开始关注数学教学的专家知能这一研究课题,涉及的研究主题包括数学教学中专家知能的测评与发展等方面.
在数学教学中专家知能的测评方面,数学教育研究者对数学教学的专家知能提出了不同的框架并进行测评.2011年,我和德国汉堡大学的凯瑟(G. Kaiser)合作出版了《数学教学中的专家知能》[17],这是全世界第一本研究数学教学的专家知能的书.书中分析了东方和西方文化背景下的数学教学专家知能的内涵及其异同.书中提到在东方背景下,研究者倾向于将教师的专家知能看作一个整体,关注教师在教学实践中的表现,其中侧重分析教师的课堂教学.在西方背景下,研究者主要将教师的专家知能分成不同的部分,包括知识、信念和教学表现等,尤其是关注教师的知识.
研:在东方背景下,数学教学中专家知能的测评方面有哪些主要的研究?
李:2009年,我和日本筑波大学的清水(Y. Shimizu)合作在杂志制作了关于中国、日本和韩国等东亚国家数学优质课的专辑,这一专辑探讨了东亚各国数学优质课的界定、特点及其开发方式[18].其中清水的研究发现重视学生的思维是日本优质课堂的关键[19],韩国国立教育大学的彭(J. Pang)的研究发现韩国优质课堂教学的重要特征之一为学生在教师的指导下参与数学思考[20].
之后,在《数学教学中的专家知能》这本书中进一步呈现了中国、日本、新加坡等东亚国家的相关研究.其中我和黄荣金等人研究了中国专家型教师的数学课堂教学特征,包括具有牢固的专业知识、恰当的识别和处理学生的学习难点、强调学生数学思维与能力的发展、使用数学问题的解决和提出来发展有效的课堂教学、强调和实施以学生为中心的教学和激发学生兴趣等[21].新加坡国立教育学院的林张(S. K. Lim-Teo)等人的研究发现新加坡的课堂重视学生的概念学习和学习动机[22].
研:在西方背景下,数学教学中专家知能的测评方面的主要研究有哪些?
李:在《数学教学中的专家知能》这本书呈现了对美国、瑞士、以色列、奥地利、加拿大等国家的相关研究.其中加拿大阿尔伯塔大学的研究者西姆(E. Simmt)将专家知能界定为指向教学的数学知识,其为多层次嵌套的结构,以学科的理解为核心,依次嵌套于由个体之间相互交流产生的集体知识;不断演化和发展的课程结构知识;更广阔的数学文化知识[23].
2008年开始,凯瑟等人参与了职前数学教师教育发展的国际比较研究项目(TEDS-M).在TEDS-M的研究中提出了一个界定职前教师掌握知识和信念的框架,其中将知识分为数学内容知识、教学内容知识和一般教学知识,而信念则包括对数学本质的信念、数学学习的信念和数学成就的信念[24].这一框架从某种程度上和专家知能很接近,只不过之前研究专家型教师,在TEDS-M中研究的是职前教师.
其后,凯瑟从事了进一步研究,提出另外一个概念:情境(situated),即根据社会文化的不同,不只将专家知能看成一个静态的概念(包括知识和信念两个部分),还要对教师进行课堂观察,观察专家知能在实际中怎么应用[25].凯瑟等西方研究者开始从原来侧重静态的认知到兼顾对课堂的观察.在2017年的第41届国际数学教育心理学大会(The International Group for the Psychology of Mathematics Education)中,凯瑟牵头,请我一起组织了一个研究论坛,主题为(未来)教师专业能力透视[26],其中即介绍了课堂观察的重要性.
美国加州大学伯克利分校的熊菲尔德(A. Schoenfeld)在课堂观察方面做了一些研究,他强调从5个不同的维度观察和分析教师的课堂教学.具体可以参阅他的“论课堂观察”这篇文章,文中综述了美国的8种课堂观察方法,他挑了其中的3种方法,通过这3种方法来观察分析同一门课,实际提供了一个工具,如果侧重观察专家型教师的这些方面,就可以得到一些结果[27].
研:在以上研究中,您提到了东西方文化背景下数学教学中专家知能测评研究的两种取向,您认为其对数学教学中专家知能的测评研究有哪些意义?
李:通过两种取向的比较可以发现,在不同社会文化背景下,对专家知能内涵的界定可能是不同的,因此就需要了解不同界定的差异.在其背后也反映了不同国家在教学的观念上有一定的差异.反思不同价值观之间的差异,以后在一些方面也许可以改进.
2.4 实践驱动与研究引领:数学教学专家知能发展研究的两类途径
研:在数学教学中专家知能的发展方面,研究者实施过哪些相关的研究?
李:在此方面,数学教育研究者提出了多种数学教学专家知能的培养方式.2011年,我和以色列的研究者埃文(R. Even)合作在杂志中发表了一个专辑,其内容涉及韩国、中国、澳大利亚、德国等东西方不同国家培养数学教学专家知能的途径,其中东方国家大部分以实践驱动,西方国家以研究项目为主[28].
在东方国家,韩国研究者彭研究了案例教学法对职前小学数学教师专家知能的影响,在案例教学中,首先基于已有的数学教学案例让职前教师展开讨论,接着让教师将在案例讨论中所学习的知识应用到教学实践中,研究结果表明经过案例教学之后,参与的职前教师对课堂分析从关注一些课堂的表面特征转向了注重数学课堂的实质特征[29].我和唐彩斌等人研究了中国的名师工作室对教师专家知能的影响,研究发现名师工作室促进了参与教师对初等数学内容及其结构的理解[30].
在西方国家,澳大利亚天主教大学的克拉克(D. Clarke)等人开展了让职前教师参与基于任务的对学生一对一评估访谈的研究项目,从中培养教师有关学生理解、评估和发展儿童思维能力的专家知能.研究结果显示职前教师通过访谈提升了学科内容知识和教学内容知识[31].美国杜肯大学的波士顿(M. D. Boston)等人开展了以数学任务为中心的教师专业发展研究项目,教师在其中学习挑选和实施具有认知挑战性的数学任务,研究结果表明,教师经过学习提高并保持了挑选高水平数学教学任务的能力[32].
2012年,在新加坡举办的PME-36中,由我牵头,凯瑟和我一起组织了一个专家知能的研究论坛,主题为数学教学中专家知能的概念化与发展[33],其中来自葡萄牙、以色列、中国台湾、韩国和新加坡的研究者也进一步介绍了其在专家知能的培养与发展方面的研究.
研:在以上研究中,您强调了东西方不同国家在数学教学中专家知能发展研究方面的两类途径,您认为其对数学教学中专家知能的发展研究有何意义?
李:通过比较不同的途径,可以明晰各种途径之间的优缺点,从而借鉴其他国家在数学教师培养方面好的举措.在职前教师培养方面,韩国做得很不错.中国为在职教师的专业发展提供了很多支持.澳大利亚和美国等国家则较为重视教师的研究性学习.
2.5 数学的“高观点”和跨学科的知识:数学教学专家知能的研究方向
研:在专家型数学教师的研究中,有关专家知能的研究始终是教育界探讨的重要话题.斯滕伯格(R. J. Sternberg)提出过专家型教师的原型观(prototype view)[34],在新时代教育改革的背景下,您认为专家型数学教师研究有哪些研究趋势?
李:在新时代教育改革的背景下,对教师的数学教学专家知能也提出了新的要求.首先,教师不仅需要掌握数学的知识,还需要有数学的“高观点”.其次,教师不只需要具备学科知识,还需要有跨学科的知识.这些新的要求也为研究者提供了新的研究方向.
研:您能否结合具体的例子给我们解释一下什么是数学的“高观点”?
李:教师需要有数学的“高观点”,即对于知识的本质具有统领性的认识.数学的内容虽然是相同的,但是看数学的角度不同、意义不同.掌握数学的“高观点”可以帮助教师理解数学的主要内容并且将数学中不同的内容联系起来.
比如数的概念,按照课程安排就是数数、一一对应、概念表征和表征之间联系,再从整数过渡到分数.但是如果掌握了单位的观点,从单位的角度去看数的概念,就会理解不管是整数或者分数,它们的大小都是以单位作为基础的,当说它的大小是1的时候,是将其作为1个单位,若说它的大小是10,是因为把它平均分成10份,每份是1个单位.
很多教师能够从单位的角度向学生讲授整数概念,但讲到整数的运算时,教师一般会着重讲解一些规则.比如,在教学中一般认为3加4等于2是错的.但是如果从单位的角度看整数的运算,就会理解任何两个整数加起来等于另一个整数都可以是对的,3加4其实可以等于2,比如3个一角,4个五分,就等于2个两角五分.
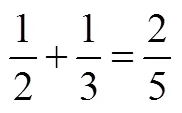
因此,强调单位的观点可以加深对数的概念、整数运算以及分数运算的理解,同时,也为学生从整数运算过渡到分数运算打下了基础.教师一旦对单位理解得比较好,他在处理整数教学和分数教学的时候,就可以帮学生很好地将两者联系起来.如果教师没有这种观念和理解,只是就事论事,教整数就是教整数,教分数就是教分数,学生就很难将两者联系起来.
研:针对跨学科的知识,您能否也给我们作进一步讲解?
李:如今,在STEM的背景下,对教师提出了新的要求.实际上,现在培养的是全科型的小学教师,而不是小学数学教师,小学职前教师除了公共课、实践课,还有语文、英语、数学、科学等课程.学科教学中讲究学科内部的完整性,而非学科之间的融合性.过去的几十年都是这么实施的,但现在情况不同了,虽然知识的获取还是需要的,但很多知识可以通过网络检索获得,不需要将大脑变成储存器来记住大量信息.同时,跨学科是现在社会发展和工作上的需要,在实际工作中很难找到一个问题是纯数学或纯化学问题,很多问题需要综合利用不同知识.因此,STEM很可能是未来教育的趋势[36].在STEM中包含了数学、科学、工程、技术,它是基于学科的,又是跨学科的,这就对教师提出新的要求,不是走进不同教室教不同的课,而是走进一个教室教STEM.因此在教师培养的时候,如果没有教跨学科的知识,还是和之前一样只是教学科知识,培养就会与社会需求脱节.我们需要培养一个不仅可以教分科教学还可以教STEM的教师.STEM教师很重要,现在很多教育学院面临着为学校输送STEM教学人才的挑战[37].
研:您在以上内容中提到数学的“高观点”和跨学科的知识,是否有相应的研究背景?对于今后此方面的研究,存在哪些困境或挑战?
李:数学的“高观点”有很多研究背景.在美国《州共同核心数学标准》中提到精确性,其含义包括概念理解的清晰性和流利性[38],指的就是从数学的“高观点”理解概念.2010年美国数学教师教育工作者协会曾发布《小学数学专家标准——教师资格认证和学位课程的参考》[39],其中数学教学内容知识的部分只是罗列了一些知识点,我觉得是不够的,在教师培养中,不仅仅需要传授知识,更需要培养观点[40].但是很多时候,教师掌握的只是知识,很难具有数学的“高观点”,课程准备与教学现实之间存在脱节现象[41].有关教师对数学的“高观点”的研究任重而道远.
跨学科知识则与目前的STEM研究结合紧密,但是,同样存在着很多挑战.首先,从专家知能的角度看,以前心理学研究中一直是先找到专家型的人才(开始是特异奇才,然后是相对的专家),数学教学专家知能的研究也是如此.但现在都找不到STEM的专家型教师,所以,研究STEM的专家知能,一个很重要的问题是找不到STEM的专家型教师.其次,以前研究专家型数学教师,数学是一个完整的知识体系,但是因为STEM不是一个学科,所以另一个问题是不知道什么是STEM知识.传统心理学研究中基于学科的专家知能,对于STEM而言都不适用,所以在研究中需要新的理论框架和导向[42].国内在STEM方面的研究起步稍晚,有很多项目可以开发.STEM为专家型数学教师的研究提供了无限的研究空间.
2.6 适应时代发展和比较文化差异:数学教学专家知能的研究建议
研:最后,您对未来专家型数学教师的研究有哪些建议?
李:首先,刚刚也讲到专家型教师需要掌握良好的数学学科知识,但还需要进一步研究专家型教师对其掌握的程度.
其次,专家知能的概念本身是发展的,需要适应时代发展的需要.以前的研究可以参照,但不能作为教条,现在培养的专家型教师和30年前培养的专家型教师是不同的,作为一个研究者要有开放的眼界.未来,肯定还会有一些从STEM角度论专家知能的研究.
再次,刚刚提到适应性专家这一概念,但还不清楚在数学教学中的适应性专家具有什么样的特质,这方面的研究有助于探索如何成为一名真正的专家型教师而不是普通的经验型教师.
同时,教学专家知能的发展也是一个值得研究的领域,研究者还需要对目前已经开发出来并行之有效的发展途径和实践有更多的认识和了解.
最后,专家知能的内涵在不同的国家和文化背景下有很大差异,因为教学本身是文化活动,所以数学教学专家知能在不同文化下应该是有差异的.因此这样的课题是很有意义的,可以进行长期研究.可能再过两三年可以出另外一本有关中国数学教学专家知能的书,甚至视角拓展一点,比较东亚国家数学教学专家知能之间的差异.《数学教学中的专家知能》研究了东西方数学教学专家知能,所以阅读的人相对而言比较多,但是每个人读了以后有什么收获就是读者的事情了.在此之后,还有很多工作,需要数学教育工作者继续努力.
3 结语
从以上访谈中可以了解到,在专家型教师的研究历程中,心理学是不容忽视的研究背景.同时,心理学中专家知能的研究方法和研究内容经历了演进和扩展的过程.当代专家型数学教师的研究主题包括数学教学中专家知能的测评与发展等方面,同时,研究者需要在不同文化背景下进行比较研究.在专家型数学教师的研究趋势中,李业平教授提到要将专家型数学教师的内涵看成一个动态发展的概念,要面向未来,适应时代发展的需要.在未来,专家型数学教师的研究是一个广阔的研究领域,专家型教师所具有的数学素养、STEM方面的专家知能、专家型数学教师的分类、数学教学专家知能的发展途径以及不同国家和文化背景下数学教师所具有专家知能的共性与差异都是未来值得研究的课题.
以上内容为中国专家型数学教师的研究提供了启示.一方面,专家型数学教师的内涵是一个不断更新发展的概念,在中国新一轮教师教育综合改革的背景下,需要结合目前对教师专业发展的需要,既要总结专家型数学教师已有的先进教学经验,也要吸收专家型数学教师对教育教学改革的真知灼见,从而为未来专家型数学教师的发展提供方向.另一方面,专家型数学教师的概念受到东西方不同社会文化的影响,中国学生在PISA等国际测试中表现良好,高质量的中国课堂教学在其中起到了关键的作用,因此,需要进一步研究中国数学教学专家知能的内涵,揭示中国数学教学专家知能发展的有效途径.从而展示专家型数学教师课堂教学的中国智慧,提供数学教师专业发展途径的中国方案.
致谢:李业平教授对此次访谈给予了大力支持并亲自审核确认了访谈录的内容.在此,对李业平教授的关心和指导表示由衷感谢.
[1] 徐红,董泽芳.我国专家型教师研究的回顾与展望[J].课程·教材·教法,2011,31(7):82–87.
[2] 中华人民共和国中央人民政府.中共中央国务院关于全面深化新时代教师队伍建设改革的意见[EB/OL].(2018–01–20)[2019–07–18].http://www.gov.cn/zhengce/2018-01/31/content_5262659.htm.
[3] 周九诗,鲍建生.中小学专家型数学教师素养实证研究[J].数学教育学报,2018,27(5):83–87.
[4] 叶立军,郑欣.专家型数学教师代数复习课提问行为研究——以一次函数和反比例函数为例[J].数学教育学报,2018,27(2):46–49.
[5] 韩龙淑.专家型教师与熟手教师运用元认知提示语的数学课堂比较研究[J].数学教育学报,2016,25(4):59–62.
[6] 叶立军,斯海霞.专家型教师数学课堂教学隐喻语言应用研究[J].数学教育学报,2013,22(1):37–39.
[7] 白改平,韩龙淑.专家型数学教师课堂教学的案例分析及特征解析[J].数学教育学报,2012,21(5):72–75.
[8] 白改平,韩龙淑.专家型—熟手型数学教师课堂提问能力的个案比较研究[J].数学教育学报,2011,20(4):16–19.
[9] 涂荣豹.专家知识的特征及其数学教学启示[J].数学教育学报,2005,14(4):13–16.
[10] 黄荣金,陈月兰,赵小平.专家教师评数学课[J].数学教育学报,2005,14(1):52–56.
[11] CHASE W G, SIMON H A. Perception in chess [J]. Cognitive Psychology, 1973, 4 (1): 55–81.
[12] CHI M T, FELTOVICH P J, GLASER R. Categorization and representation of physics problems by experts and novices [J]. Cognitive Science, 1981, 5 (2): 121–152.
[13] ERICCSON K A, KRAMPE R T, TESCHE-ROMER C. The role of deliberate practice in the acquisition of expert performance [J]. Psychological Review, 1993, 100 (3): 363–406.
[14] COOKE N J, SALAS E, CANNON-BOWERS J A, et al. Measuring team knowledge [J]. Human Factors, 2000, 42 (1): 151–173.
[15] HATANO G, INAGAKI K. Two courses of expertise [M] // STEVENSON H, ASSUME H, HAKUTA K. Child development and education in Japan. New York: Freeman, 1986: 262–272.
[16] LEINHARDT G. Math lessons: A contrast of novice and expert competence [J]. Journal for Research in Mathematics Education, 1989, 20 (1): 52–75.
[17] LI Y, KAISER G. Expertise in mathematics instruction: An international perspective [M]. New York: Springer, 2011.
[18] LI Y, SHIMIZU Y. Exemplary mathematics instruction and its development in selected education systems in East Asia [J]. ZDM, 2009, 41 (3): 257–262.
[19] SHIMIZU Y. Characterizing exemplary mathematics instruction in Japanese classrooms from the learner’s perspective [J]. ZDM, 2009, 41 (3): 311–318.
[20] PANG J. Good mathematics instruction in South Korea [J]. ZDM, 2009, 41 (3): 349–362.
[21] LI Y, HUANG R, YANG Y. Characterizing expert teaching in school mathematics in China: A prototype of expertise in teaching mathematics [M] // LI Y, KAISER G. Expertise in mathematics instruction: An international perspective. New York: Springer, 2011: 167–195.
[22] LIM-TEO S K, CHUA K G, YEO J K K. Perceptions of school mathematics department heads on effective practices for learning mathematics [M] // LI Y, KAISER G. Expertise in mathematics instruction: An international perspective. New York: Springer, 2011: 221–241.
[23] SIMMT E. Teacher expertise explored as mathematics for teaching [M] // LI Y, KAISER G. Expertise in mathematics instruction: An international perspective. New York: Springer, 2011: 151–164.
[24] BLÖMEKE S, KAISER G. Theoretical framework, study design and main results of TEDS-M [M] // BLÖMEKE S, HSIEH F J, KAISER G, et al. International perspectives on teacher knowledge, beliefs and opportunities to learn. Dordrecht: Springer, 2014: 19–47.
[25] KAISER G, BLÖMEKE S, KÖNIG J, et al. Professional competencies of (prospective) mathematics teachers——Cognitive versus situated approaches [J]. Educational Studies in Mathematics, 2017, 94 (2): 161–182.
[26] KAISER G, LI Y. Perspectives on (future) teachers’ professional competencies [M] // KAUR B, HO W K, TOH T L, et al. Proceedings of the 41th conference of the international group for the psychology of mathematics education (Vol. 1). Singapore: PME, 2017: 81–84.
[27] SCHOENFELD A H, FLODEN R, CHIDIAC F, et al. On classroom observations [J]. Journal for STEM Education Research, 2018, 1 (1–2): 34–59.
[28] LI Y, EVEN R. Approaches and practices in developing teachers’ expertise in mathematics instruction: An introduction [J]. ZDM, 2011, 43 (6–7): 759–762.
[29] PANG J. Case-based pedagogy for prospective teachers to learn how to teach elementary mathematics in Korea [J]. ZDM, 2011, 43 (6–7): 777–789.
[30] LI Y, TANG C, GONG Z. Improving teacher expertise through master teacher work stations: A case study [J]. ZDM, 2011, 43 (6–7): 763–776.
[31] CLARKE D, CLARKE B, ROCHE A. Building teachers’ expertise in understanding, assessing and developing children’s mathematical thinking: The power of task-based, one-to-one assessment interviews [J]. ZDM, 2011, 43 (6–7): 901–913.
[32] BOSTON M D, SMITH M S. A “task-centric approach” to professional development: Enhancing and sustaining mathematics teachers’ ability to implement cognitively challenging mathematical tasks [J]. ZDM, 2011, 43 (6–7): 965–977.
[33] LI Y, KAISER G. Conceptualizing and developing expertise in mathematics instruction [M] // TSO TAI-YIH. Proceedings of the 36th conference of the international group for the psychology of mathematics education (Vol. 1). Taipei: PME, 2012: 121–124.
[34] STERNBERG R J, HORVAT J A. A prototype view of expert teaching [J]. Educational Researcher, 1995, 24 (6): 9–17.
[35] 陈蓓,章飞.分数意义建构的顺序及对教科书设计的建议[J].数学教育学报,2018,27(4):58–61.
[36] 李业平.STEM教育研究与发展:一个快速成长的国际化领域[J].数学教育学报,2019,28(3):42–44.
[37] 王科,李业平,肖煜.STEM教师队伍建设:探究美国STEM教师的工作满意度[J].数学教育学报,2019,28(3):62–69.
[38] 廖运章.美国《州共同核心数学标准》的内容与特色[J].数学教育学报,2012,21(4):68–72.
[39] 汤志娜,卢建川.美国AMTE《小学数学专家标准》的背景与内容及其特点[J].数学教育学报,2015,24(2):35–39.
[40] LI Y. Mathematical preparation of elementary school teachers: Generalists versus content specialists [J]. School Science & Mathematics, 2010, 108 (5): 169–172.
[41] 邹佳晨,姜浩哲,沈中宇.新时代华人数学教育研究的特点与展望——“第三届华人数学教育大会”综述[J].数学教育学报,2019,28(2):99–102.
[42] LI Y, SCHOENFELD A H. Problematizing teaching and learning mathematics as “given” in STEM education [J]. International Journal of STEM Education, 2019, 6 (1): 1–13.
Research on Expert Mathematics Teachers: Trends and Prospects——An Interview with Professor LI Ye-ping
SHEN Zhong-yu1, LIU Si-lu2, ZOU Jia-chen2
(1. School of Mathematical Science, East China Normal University, Shanghai 200241, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China)
Research on expert mathematics teachers is an important topic in educational research. Through interviewing Professor LI Ye-ping at Texas A&M University, this paper probes deeply into the research process and contemporary research of expert mathematics teachers and looks forward to future research on expert mathematics teachers. In the view of Professor Li, psychological research provides an important research background for research of expert teachers; the research topics of expert mathematics teachers include conceptualizing and developing expertise in mathematics instruction; and, under the context of education reform in the new era, research of expert mathematics teachers should face the future and meet the needs of present developments. Professor Li also provides suggestions for the future research about expert mathematics teachers.
expert mathematics teachers; expertise; development approach; international comparison
G451
A
1004–9894(2021)02–0061–06
沈中宇,刘思璐,邹佳晨.专家型数学教师的研究与展望——李业平教授访谈录[J].数学教育学报,2021,30(2):61-66.
2020–10–20
上海市第四期双名工程高峰计划项目——上海市中小学数学专家型教师课堂教学表征研究;上海高校“立德树人”人文社会科学重点研究基地之数学教育教学研究基地研究项目——数学课程与教学中落实立德树人根本任务的研究(A8);云南省哲学社会科学教育科学规划项目(青年项目)——基于实践共同体的职前职后教师专业发展一体化研究(AD19002)
沈中宇(1991—),男,江苏苏州人,博士生,主要从事数学教师教育、数学史与数学教育研究.
[责任编校:周学智、陈隽]
