不同几何尺寸金刚石压头对洛氏硬度值影响的三维有限元数值研究
2021-04-29吴禹,薛瑞
吴 禹,薛 瑞
1. 重庆市计量质量检测研究院, 重庆 401123; 2. 重庆机场集团有限公司, 重庆 401120
压痕试验是一种简单、 高效的评价材料力学性能的手段, 其试验结果可以反映出关于弹性模量、 屈服应力、 加工硬化等材料的整体力学性能, 因而其应用的历史已近百年[1-2].
所有关于材料性能研究及生产质量控制中所得到的硬度试验结果的校准量值都是经硬度标准装置溯源至国家硬度基准. 对硬度标准、 基准装置而言, 压头几何尺寸引入的不确定度分量在测量结果的不确定度评定[3]中都显得不可忽略. 而在硬度试验的不确定度评定中, 常采用综合评定法或直接评定法[4], 对洛氏硬度国家基准、 副基准而言, 其标准不确定度的评定则需要采用直接评定法. 而当我们未知被测量与影响量间的函数关系时, 洛氏硬度试验中压头几何尺寸引入的不确定传播系数则不易从数学模型导出, 这对不确定度的直接评定造成了难度. 另外, 在相关文献中, 也仅是根据已有的经验公式计算得出了压头对硬度示值影响很大的结论, 并未能深入研究材料应力分布情况及压头几何尺寸对硬度值测量结果的不确定度分析, 在进行压头圆锥角及顶端球面半径系统误差的合成时, 一般也忽略了二者误差因素间可能存在的耦合影响. 在有限元方面[5], 过去限于计算机的储存空间及运算速度, 多在二维进行加、 卸载模拟, 三维模型的建立与计算则比较困难[6-7]. 对压痕弹塑性问题则是一非线性问题[8], 再加上压头复杂的几何特征(球面和锥面), 理论精确解是显然无法获得的. 因此, 本文利用ANSYS建立了对压痕试验加、 卸载过程的三维有限元模型, 通过回归分析获得了金刚石压头圆锥角度偏差及顶端球面半径偏差对硬度值的一元线性回归方程, 进而得到了有关压头圆锥角度和顶端球面半径对硬度影响的一些结论, 并且计算出不确定度评定中压头相关的不确定传播系数以及压头引入的相对标准不确定度分量等, 为其他对硬度测量结果的不确定度评定提供一些参考.
1 试验设计
本试验设计硬度样块材料为合金钢, 其淬火温度为870 ℃, 淬火介质为油, 回火温度为480 ℃. 根据热处理相关资料显示设计硬度为中硬度, 按照规范要求[9], 对工作硬度计, 金刚石圆锥体压头的两相对面夹角应为(120±0.35)°, 顶端球面半径平均值应在(0.2±0.01) mm以内. 对标准硬度机, 压头圆锥角平均值应为(120±0.10)°, 顶端球面半径平均值应在(0.2±0.005) mm以内, 并且与基准压头取得的硬度值之差相比, 最大允许误差分别为±0.8,±0.4 HR. 针对本文研究的目的及方便对数据结果进行回归分析, 设计中硬度下, 等距选取压头圆锥角分别为120.35°,120.17°,120.00°,119.83°,119.65°; 压头顶端球面半径分别为0.210,0.205,0.200,0.195,0.190 mm; 以及二者耦合作用下进行洛氏C标尺硬度试验.
2 有限元非线性计算及结果
2.1 有限元模型的基本假设及建立
为了提高模型计算精度、 减小计算成本, 采用ANSYS有限元软件, 利用模型受力的对称性, 建立了1/4硬度压痕三维模型. 同时, 为计算简便, 模型压头选择为刚体, 假定硬度块与试验台台面接触良好, 无任何相对滑动. 由于塑性变形规律远比弹性变形复杂得多, 为了使复杂问题得以合理范围内解决, 并能依靠有限元数值方法模拟三维情况下的洛氏硬度试验, 本文根据塑性力学理论, 对金属硬度块采用简化的线性强化弹塑性体模型的应力应变曲线, 利用ANSYS有限元软件模拟对材料的压痕硬度试验, 首先需解决硬度参数化问题. ANSYS本身的输入参数中不存在硬度指标, 不能直接对材料硬度进行FEM数值模拟.
计算模型共有单元数62 729个. 硬度块底面的全部节点上施加全约束, 在两个1/4模型的中面上施加垂直于中面的位移约束, 对压头的刚性接触面的主控关键点设置竖直向下的分级荷载(包含加、 卸载过程), 其网格及约束见图1和图2.
考虑到压头压入过程中还存在接触非线性及大变形问题, 故在已建立的硬度块实体单元表面及压头表面分别覆盖、 划分一层目标面TARGE170单元及接触面CONTA174单元, 以形成接触对. 计算过程中采用大变形理论.

图1 三维有限元模型及网格划分(1/2模型局部)

图2 三维模型边界条件示意图(1/4模型)
2.2 有限元非线性计算结果分析
2.2.1 洛氏硬度试验下压痕周围mises应力变化规律及卸载后残余mises应力分布
图3给出了标准金刚石圆锥体压头下洛氏硬度试验后残余mises应力分布云图, 图4为基于有限元计算结果通过MATLAB绘制的压痕形貌图, 图5绘出压痕过程中荷载—压深位移曲线.
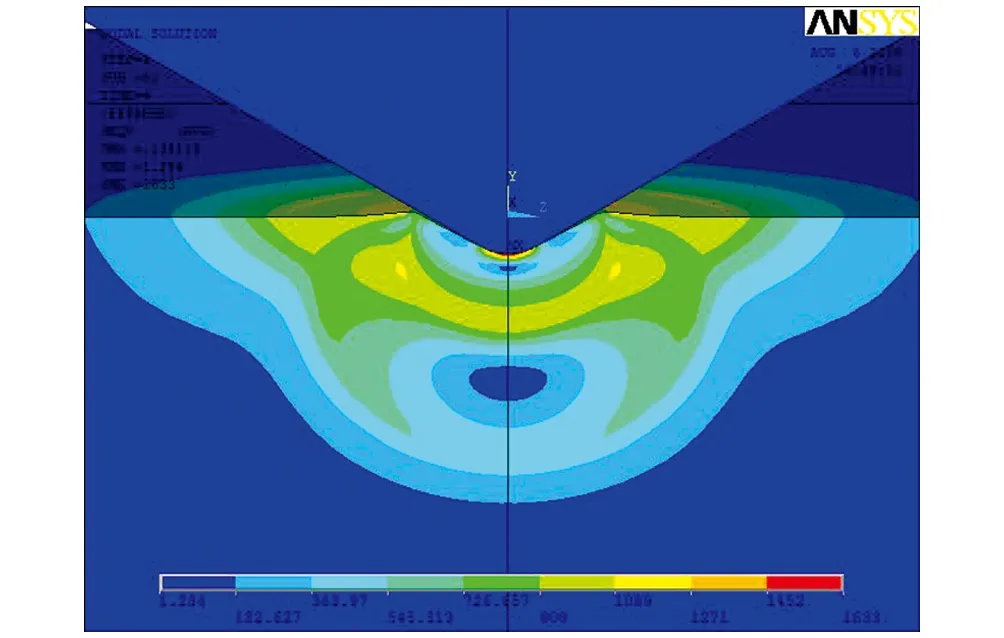
图3 卸载后残余mises应力云图(局部)

图4 卸载后压痕形貌图(1/2模型)

图5 荷载—压深位移曲线
在初试验力作用下, 压头尖端处附近的材料mises应力最大, 此时压头压入量较小, 而在主试验力的叠加作用下, 依旧是压头尖端处附近的应力最大, 只是受压头压入的影响, 压痕附近材料逐步由弹性阶段过渡为弹塑性阶段, 此时塑性区范围很大, 压头压痕附近的应力集中更为明显, 应力变化梯度更大并且在材料表面存在局部堆积的现象. 由塑性变形基本规律分析知, 压头尖端附近塑性区存在较高的三轴压应力, 随着变形量的增大, 将在压头尖端附近的金属材料中发生大量的位错, 导致位错密度增大, 位错间的弹性作用对位错发生起着阻碍作用, 形成位错强化, 使得压头顶端球形压痕面的正压力不断升高, 若顶端球面半径变大, 则此正压力越大. 在主试验力及总试验力卸载后, 材料内部仍然存在分布较为复杂的残余应力. 另外, 从图中可观察到本文所建模型不存在基底效应, 所选取试件的尺寸完全满足本文有限元分析的要求. 并且由图5可知, 在本硬度试验过程中, 压深主要由材料的塑性变形产生, 其中由材料弹性变形引起的压深位移占总位移比例较小.
2.2.2 不同金刚石圆锥体压头尺寸下用压痕表征的硬度值规律
本文通过有限元数值分析分别得到了试验设计条件下的压头底部位移, 由此计算出各个情况下的洛氏C标尺下的硬度值(表1). 各工况下的压头底部位移及硬度值散点图如图6-图9. 图10给出了金刚石圆锥体压头在本试验设计圆锥角角度及顶端球面半径变化下的几何示意图.
由图6-图9可知, 初试验力加载下压头底部位移受圆锥角角度影响不大, 而随顶端球面半径的增大呈减小的趋势, 当圆锥角度偏差及顶端球面半径偏差耦合作用时, 其曲线与单受顶端球面半径影响的曲线接近. 在主试验力加载及主试验力卸载两种条件下, 压头底部位移随圆锥角角度、 顶端球面半径的增大呈减小的趋势, 二者耦合作用时, 其趋势更为明显. 结合图8分析, 在初试验力加载下, 压痕深度大部分位于压头顶端球面部位附近, 此时, 主要为球面接触阶段, 所以该条件下, 压头底部位移受圆锥角角度的影响并不明显, 反而对顶端球面半径的改变比较敏感. 随着压痕深度的增加, 压痕过程从开始的球面接触逐步过渡为锥面接触. 对高硬度材料而言, 压痕深度较低硬度材料的压痕深度浅, 故硬度值受压头顶端球面半径的影响更大, 而对低硬度材料, 锥面接触占优势的情况下, 硬度值受压头圆锥角角度的影响更大. 另外, 从图9可知, 当圆锥角或顶端球面半径为正偏差时, 硬度值也呈正偏差.
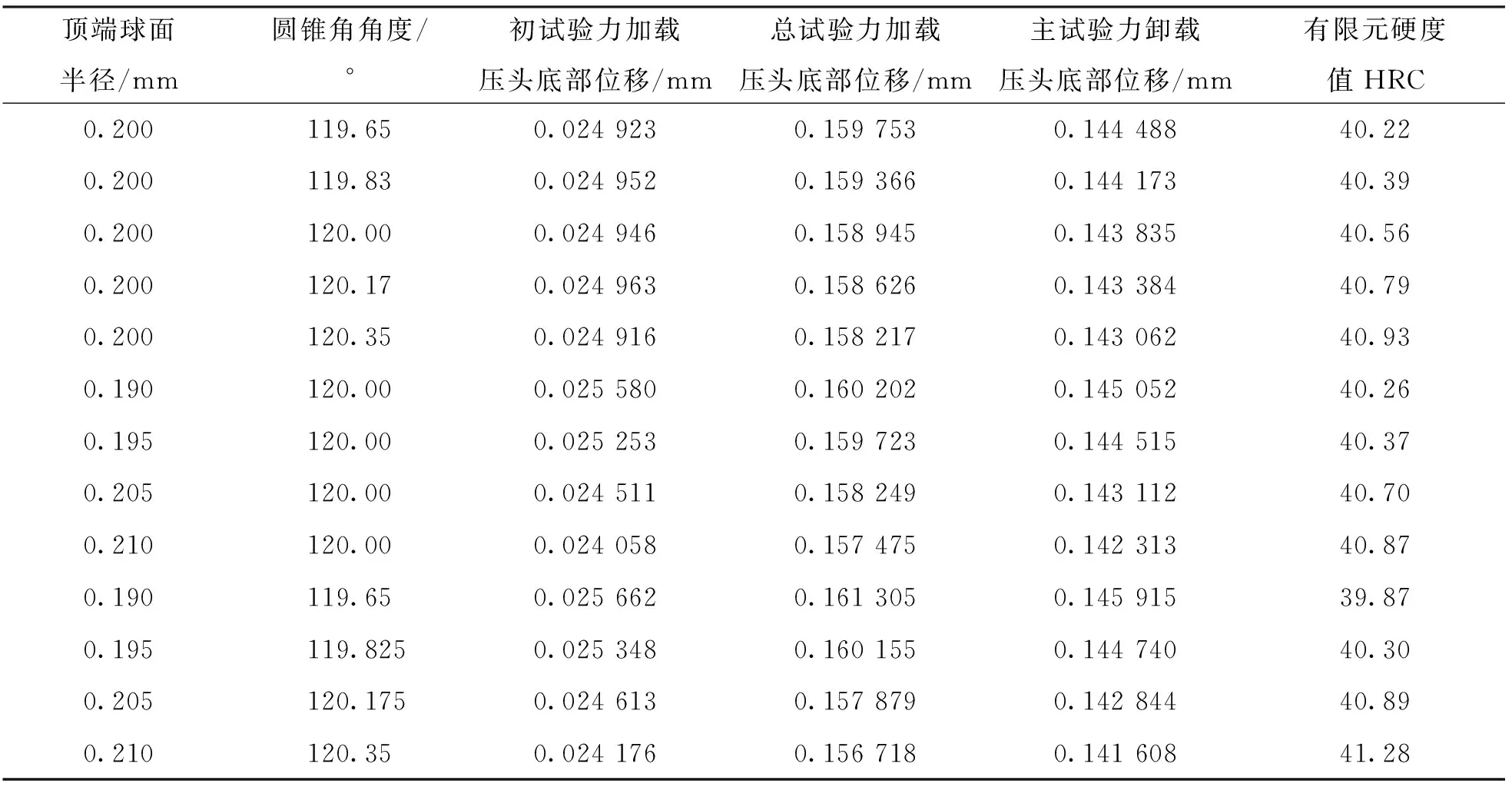
表1 计算结果

图6 初试验力加载下各工况压头底部位移

图7 总试验力加载下各工况压头底部位移

图8 主试验力卸载下各工况压头底部位移

图9 各工况下有限元硬度值
2.2.3 有限元计算结果的线性回归分析
为了寻求压头底部位移与圆锥角角度、 顶端球面半径及两者偏差耦合作用时的内在关系, 利用回归分析求得各压头位移关于各变量的线性回归函数. 为了知道直线是否基本符合两者之间的客观规律, 另外还进行了回归方程的显著性检验(F检验及r检验).
一元线性回归方程为
y=bx+b0
(1)
从回归分析结果可知, 除初试验力加载下圆锥角角度拟合外, 在F分布显著性水平0.01条件下, 各回归分析的结论都是高度显著, 说明各变量在计算范围内与压头底部位移可以认为是存在线性关系的, 从局部范围来看, 各变量的一次项对压头底部位移的影响是主要的. 求得回归系数后, 可在计算范围内由回归方程计算出任意角度、 半径偏差量下压头底部位移的回归值, 最小二乘法求得的最佳解使计算结果合理可靠, 提高了有限元分析的准确度.

图10 压头几何尺寸示意图

表2 回归分析部分结果
2.2.4 压头圆锥角偏差及顶端球面半径偏差之间对硬度值的耦合效应
本文有限元计算中, 分别单独分析了压头在圆锥角偏差下及顶端球面半径偏差下对测量结果的影响. 假设以上两项误差都是相互独立的并且可看作固定已知的系统误差, 按照误差的传递规律, 总的系统误差值可由式(2)计算:
(2)
然而, 压头圆锥角偏差及顶端球面半径偏差之间若看作是相互独立的, 则意味着忽略了二者误差因素间可能存在的耦合影响. 将式(2)计算的总的系统误差值与本文有限元数值分析结果的回归值进行比较, 结果如表3.

表3 耦合效应下有限元数值分析结果与合成的总系统误差对比
从表3可知, 考虑圆锥角偏差及顶端球面半径偏差耦合作用下的有限元数值分析得出的是考虑了二者误差因素间耦合影响的硬度值计算结果, 硬度偏差回归值为1.369 HR. 而若依据系统误差的传递规律, 计算出总的系统误差合成后为1.338 HR, 说明圆锥角偏差与顶端球面半径偏差两者之间存在正耦合效应. 在进行圆锥角及顶端球面半径系统误差的合成时, 考虑耦合效应计算出硬度值的系统误差比不考虑耦合效应的计算结果偏高2.3%.
2.2.5 压头圆锥角及顶端球面半径对硬度值的灵敏系数分析
合成标准不确定度是由各标准不确定分量合成而来, 合成标准不确定度计算公式可写为
(3)
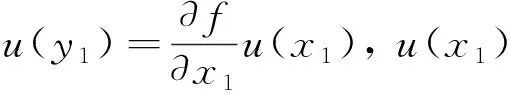

表4 灵敏系数
2.2.6 由压头几何尺寸引入的不确定度分量
基于前文对有限元数值分析结果的回归值计算, 假设检定规程所允许偏差范围内压头的几何尺寸偏差呈正态分布, 可计算出由合格压头的圆锥角、 顶端球面半径分别引入对硬度值的标准不确定度分量.
对工作洛氏硬度计而言, 压头圆锥角允许误差为Δα=±0.35°, 同时压头顶端球面半径允许误差为Δr=±0.01 mm, 因而由圆锥角、 顶端球面半径引起的对洛氏C标尺中硬度值影响的极限误差分别为δ1=±0.90%和δ2=±0.75%, 其概率分布为正态分布, 置信水平P=99%, 包含因子KJ=2.58, 则相对标准不确定度分量u1=0.35%,u2=0.29%. 对中硬度(45 HR), 若按系统误差的传递规律计算, 其被检合格的压头与标准压头比较的示值最大误差为±0.74 HR.
对标准洛氏硬度机而言, 压头圆锥角允许误差为Δα标=±0.10°, 同时压头顶端球面半径允许误差为Δr标=±0.005 mm, 因而由圆锥角、 顶端球面半径引起的对洛氏C标尺中硬度值影响的极限误差分别为δ1标=±0.26%和δ2标=±0.37%. 同理可得, 其相对标准不确定度分量为u1标=0.10%,u2标=0.15%. 对中硬度(45 HR), 若按系统误差的传递规律计算, 其被检合格的压头与标准压头比较的示值最大误差为±0.28 HR.
对洛氏硬度国家基准、 副基准, 其压头一般经过精选, 严格保证其几何形状参数, 标准值偏差较小. 对此, 可参考相关文献[10]提供的较为先进的压头几何尺寸测量方法及数据处理技术, 得到压头组的实际几何尺寸偏离标称值的区间半宽, 再参照本文所给的回归方程计算其对硬度值影响的极限误差, 由此计算基准压头组由压头几何尺寸引入的相对标准不确定度分量等结果.
3 结论与展望
1) 大部分求解问题的有限元模型[11-12]都为涉及接触问题的二维1/2模型, 施加荷载为简化的线荷载力. 在一般的计算模拟中, 多将压头与金属材料的接触过程简化成了赫兹接触或类似的形式, 一定程度上简化了计算的复杂性, 但却不能准确地反映压头压入过程中的应力应变响应. 本文利用有限元对压痕硬度试验的加、 卸载进行了三维情况下的深入模拟, 利用数值模拟展现压头下不同位置材料的状态变化过程, 探索了利用有限元数值分析方法进行硬度压痕过程的三维模拟的可行性. 这种数值分析不仅可避免利用解析的方式分析问题所带来的极大困难, 更可作为真实硬度压痕试验不便或不可能完成的研究工具或手段. 它能不受其他试验条件的影响, 极方便地构造单变量影响因素的硬度模拟试验, 完成了一些真实压痕试验中不便完成的研究. 在实际压痕硬度试验中, 标准洛氏硬度机中使用的标准金刚石圆锥体压头一般需要进口, 并且也非完全理论上的对称. 在硬度实测试验中, 标准洛氏硬度机及被测硬度块的均匀性也将在测量结果中引入不可忽视的标准不确定分量, 这都将不利于得到不同压头尺寸下不同压痕表征的硬度值规律.
2) 按照本文获得的有限元计算结果可得到如下主要结论: 压头圆锥角偏差及顶端球面半径偏差之间存在正耦合效应, 考虑耦合效应计算出硬度值的系统误差比不考虑耦合效应的计算结果偏高2.3%; 压头圆锥角角度与硬度值之间的灵敏系数为59.86 HR/rad, 压头顶端球面半径与硬度值之间的灵敏系数为0.030 4 HR/μm, 可参考对已知几何尺寸偏差压头的试验结果进行修正, 另外可参考在直接评定法的不确定度评定中参与计算; 获得了中硬度下工作洛氏硬度计由圆锥角、 顶端球面半径引入的相对标准不确定度分量, 分别为0.35%和0.29%, 中硬度下标准洛氏硬度机由圆锥角、 顶端球面半径引入的相对标准不确定度分量为0.10%和0.15%, 其可对其他洛氏C标尺硬度值测量结果不确定度评定计算由压头引入的标准不确定度分量时提供参考.
3) 目前, 还没有一个模型可以准确模拟金属材料全应变范围的应力应变关系, 5个基本参数的全应力应变模型运用在数值模拟时让计算变得较为复杂, 当材料由弹性变形转变为小范围甚至大范围大应变的塑性变形时, 需要依靠精确描述的大塑性变形下材料的应力应变关系曲线, 这样才可以进一步提高应力分布的数值模拟精度. 本文根据塑性力学对材料的理想化处理, 采用Mises屈服条件, 采用简化的线性强化弹塑性体模型是为了节省这类复杂非线性问题的计算时间并在增量迭代求解过程中得到收敛.
许多学者在对材料的应力应变模型的研究中, Ramberg和Osgood最早提出了R-O方程, 用于计算金属的应力应变曲线, 该模型在塑性应变小于0.2%时可以准确计算应力, 对超出部分应力计算值偏高[13]. Macdonald和Mirambelle等都提出过修正的应力应变曲线[14-15], 但方程过于复杂, 不利于数值模拟计算. Quach提出的适用于大应变范围的三段式应力应变曲线, 将超出2%的塑性应变简化为直线, 在以后的三维数值模拟研究中, 可以在此应力应变关系上, 收集尽可能多的金属拉伸试验数据, 并不断完善应力应变关系模型, 以得到更高的数值模拟精度. 本文进行的数值模拟计算, 是借助有限元软件得到三维情况下复杂非线性问题的理论近似解, 下一步工作可以进行一些有必要的实测试验研究, 以增加研究的完整度.
