基于惯性椭圆拟合的小目标姿态测量方法
2021-04-29金国强陈宇璇竺长安
金国强,陈宇璇,阚 艳,金 一,竺长安
(1.中国科学技术大学工程科学学院,合肥 230026;2.国营芜湖机械厂,安徽芜湖 241000)
0 概述
在有关飞行器的研究中,为了优化目标运动轨迹,从而更精确地进行故障分析并评价目标性能,需要对飞行目标的姿态相关参数进行准确测量[1],这也是军事领域的一大需求,对火箭、导弹等飞行中的目标状态进行测量和实时分析,有利于对其性能进行准确评估,实现设备优化与故障分析的目的。传统的测量手段,如在飞行器中内置高精度陀螺仪[2]、利用全球卫星定位系统[3]等,都需要在目标中安装传感器,成本过高,并且由于飞行目标运动速度极高,会导致无线传输信号中断,使得测量可靠性降低。光学测量技术具有非接触、精度高、可复现、全场测量以及不受电磁环境影响等优点,在实际中被广泛应用。针对导弹、火箭等轴对称目标,常用的姿态测量方式为面面交汇法[4],这种方法利用不同位置的多个相机同时拍摄目标,识别每个相机中的目标中轴线,然后计算出目标在空间中的实际姿态。面面交汇法计算目标姿态的关键步骤是获得每幅图像中目标的中轴线坐标,单幅相机所摄图像中目标姿态的计算精度对最后的姿态测量准确度有直接影响。
目前常用的光测方法多数未针对缺失纹理细节特征的目标的角度和位置测量进行研究。文献[5-7]将拍摄到的目标看作运动的点以进行处理,记录飞行目标的轨迹和速度等参数,但其无法获得角度信息,使得对目标的飞行状态分析不充分。文献[8-9]先提取轮廓特征点,然后通过特征匹配的方式获取当前姿态。文献[10-11]融合多种轮廓细节特征得到目标姿态,但其较难应用于细节缺失目标。文献[12]根据目标图像灰度的不同将目标分为不同部分,并分别利用轮廓信息进行测量以得到最终姿态。文献[13]利用矩形拟合目标轮廓并利用迭代的方法得到目标的中轴线,但是该方法对迭代初值敏感。文献[14]利用快速边缘特征描述来寻找目标的轮廓线从而得到目标的姿态。文献[15]利用梯度方向直方图来提取目标的上下边缘线,从而得到目标的姿态角度。文献[16]利用霍夫变换拟合目标边界轮廓以进行姿态测量。上述利用轮廓信息的方法必须事先知道目标物体的细节特征并且物体在图像中的成像足够大,才能有效计算目标飞行时的角度,对于轮廓成锯齿状态的小目标,利用轮廓信息得到的目标姿态将存在一定误差。
在导弹、火箭卫星发射以及高速航天器跟踪拍摄等情况下,为保证安全并满足一定的拍摄范围,相机一般设置很远,图像中目标小且模糊。同时,由于拍摄背景(天空)比较亮,背景与目标对比度大,目标物体的细节特征将会进一步丢失。在极端情况下,目标最窄处在视野中只有几个像素值,仅剩轮廓特征,且轮廓边缘会有锯齿状干扰项,常见的利用目标细节特征的方法将使用受限。如何利用相机设置和图像处理方法,在分辨率有限的图像中准确提取目标姿态,是提升小目标姿态测量准确度的难点所在。
本文提出一种“追踪-分割-测量”一体化的小目标姿态测量方法。对图像中纹理信息丢失的极小目标的中轴线和中心点进行提取,为后续目标空间姿态计算提供数据。利用高速摄像机拍摄高速运动中的目标,通过目标跟踪算法进行飞行目标的自动追踪,采用非面积极大区域抑制法完成目标前景提取,通过惯性椭圆计算得到目标在图像中的姿态角度,从而实现远距离高速目标的飞行姿态测量。
1 图像获取及目标追踪
本文实验系统装置示意图如图1 所示,使用高速相机拍摄飞行中的目标,如高速移动的导弹等。本文中的高速相机型号为千眼狼5F01,具有很高的拍摄频率,适用于对高速运动的物体和快速变化的过程进行拍摄采样,获取目标更多的飞行细节信息。此外,由于高速相机获取的图像每帧之间差距较小,降低了后续追踪和目标前景提取的难度。本文方法的目标是从单个相机拍摄到的二维图像中获取目标姿态,即提取目标的中轴线,因此,下文实验中都只取单个相机拍摄到的图像作为研究对象。

图1 系统装置示意图Fig.1 Schematic diagram of system device
在使用高速相机获得目标图像后,需要对拍摄的运动目标进行追踪和检测。本文利用核相关滤波器(Kernel Correlation Filter,KCF)[17]算法进行目标跟踪,KCF 是一种判别式跟踪方法,通过训练一个判别器来判断候选框中的像素是目标还是背景[18],从而实现目标识别,其原理如下:
给定训练样本集(xi,yi),对于线性情况,定义回归函数为f(xi)=ωTxi,其中,ω表示列向量权重系数。误差函数表示为:

其中,λ是正则系数,用于控制过拟合现象。利用脊回归原理求得复数域的解为:

其中,X=[x1,x2,…,xn]T是样本的向量化表示,XH表示复共轭转置矩阵,y是列向量,表示对应的标签。为了简化上述方程的求解过程,KCF 算法将样本输入转换为循环矩阵,利用循环矩阵的傅里叶变换性质[19]:

即循环矩阵可以在傅里叶矩阵中进行对角化。在式(3)中,“^”表示傅里叶空间的变量,F是一个与输入无关的常数矩阵,将式(3)代入式(2)中,可以得到脊回归解的简化表达:

其中,⊙表示元素之间的值相乘。KCF 算法利用较为简单的元素间运算替换原表达式(式(2))中的矩阵求逆运算,从而大幅降低运算量并提升运算速度。
对于非线性情况,只需引入非线性核函数即可对非线性空间样本进行拟合。利用KCF 算法可以自动地从图像序列中找到目标区域并截取目标区域,同时保留其坐标,为后续计算提供数据。
2 小目标姿态计算算法
2.1 基于非面积极大区域抑制法的目标提取
在远距离拍摄目标时,极端情况下目标物体的最窄处在拍摄视频中仅占几个像素,在边界处锯齿状明显,如图2(a)所示。由于目标图像本身所含像素数少,直接使用原始图片容易提高误差,因此本文采用对图像进行插值放大的方式降低边缘锯齿状带来的误差,提升亚像素精度。图2(b)、图2(c)是未经插值亚像素提升的处理结果,图2(d)、图2(e)是经过5 倍插值放大后的结果。此外,目标提取对图像噪声比较敏感,本文选用中值滤波[20]作为图像的噪声处理方法,该方法可以有效去除图像中的椒盐噪声,在平滑图像的同时保留边界信息。为了提取图像中的目标区域,对图像进行二值化,可以看到二值化后的图像中除了目标区域外还含有其他区域,如图2(b)、图2(d)所示。考虑到目标在二值化后的图中所占面积最大,本文利用非面积极大区域抑制法去除面积小的区域,仅保留面积最大的区域,从而有效消除其他干扰并分割出目标区域,如图2(c)、图2(e)所示。最后结果显示,对目标插值进行放大可以有效减小边缘锯齿,但是由于目标本身像素数少,在插值处理后的目标图中仍可以看出边缘存在不规则的形状。

图2 目标前景提取流程Fig.2 Target foreground extraction procedure
2.2 基于轮廓提取的角度信息计算
在基于数字图像的目标姿态测量方面,利用图像中的直线信息进行姿态测量是常见的测量手段,霍夫变换法[21]是一种应用广泛的直线检测方法,但是其不适用于小目标情况。图2(c)、图2(e)是实际拍摄图像分割后的效果,由于原始图像中目标尺寸很小,因此在进行分割后边缘不可避免地会产生不规则形状,在这种情况下霍夫变换法不再适用。图3所示为利用霍夫变换法对图2(e)进行姿态测量的中间结果,图像边缘是利用霍夫变换法提取到的拟合直线,可以看出,当目标拍摄距离远且边缘不整齐时霍夫变换法的直线提取会有偏差,导致出现测量误差。一方面,测得的不平行线段会影响目标倾角的计算,另一方面,这种情况也会导致目标中轴线和中心点提取错误。

图3 霍夫变换法测量示意图Fig.3 Schematic diagram of measurement of Hough transform method
为解决上述问题,本文利用目标整体轮廓信息进行目标的姿态识别。导弹、火箭等飞行器的外形近似为长圆柱体,利用该特点,可以计算分割后目标的惯性椭圆[22-23],以椭圆方位角作为目标在相机平面内的姿态角,椭圆的中心点作为目标在当前帧的位置。惯性椭圆常利用图像的矩来表示,图像的矩定义为:

其中,I(x,y)代表图像上的灰度值,i、j代表矩的阶数。特别地,当图像是二值图时,M00代表图像上白色区域的总和,即区域图像的面积。利用图像的一阶矩可以计算出二值图像的重心:

其中,xc、yc分别为重心的横、纵坐标。图像的协方差矩阵具有平移不变性,可以更好地描述二维像素的分布情况,如下:

对于二维图像,协方差矩阵的特征向量表示其惯性椭圆的长轴和短轴,因此,可以直接计算得到方向角度:

对于轴对称物体而言,椭圆的长轴与目标轴线方向一致,惯性椭圆长轴的方向角度即目标在图像中的方向角度。利用目标图像的轮廓信息可以一次性得出目标的位置和角度信息,从而简化目标姿态计算过程。本文小目标姿态计算算法流程如图4 所示。
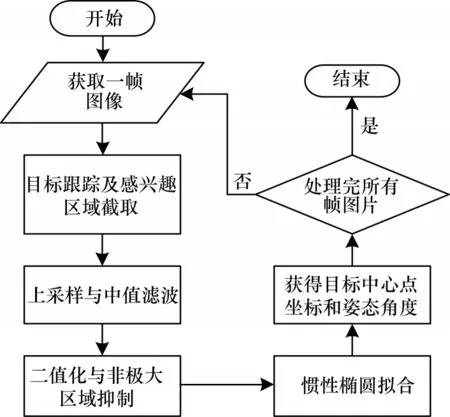
图4 小目标姿态计算算法流程Fig.4 Procedure of the small targets attitude calculation algorithm
3 测量结果与分析
3.1 仿真验证
在导弹等小目标的姿态测量过程中,目标图像需经过图像采集、追踪及裁剪、图像预处理和姿态测量4个步骤。本文利用绘图软件制作不同情况下的导弹模拟图,以验证本文所提算法的测量精度。首先制作原始数据集,根据常见的导弹形态绘制模型,如图5 所示,长宽比为8∶1,从与竖轴夹角为0°开始每隔5°生成一张图片,直到180°,共37 张图片,原始图片分辨率为3 000 像素×3 000 像素,图5(a)为部分数据集图片。

图5 部分仿真图片Fig.5 Some simulation images
3.1.1 分辨率及重构放大系数对测量精度的影响
在拍摄中得到的对象图像尺寸不一,在算法处理时也会使用不同尺度的重构放大系数,本文分析分辨率和重构放大系数对算法精度的影响。先将原图按不同尺寸缩放系数缩小到不同的分辨率,模拟实际图像采集过程中不同分辨率的目标图像,然后对其进行双线性插值放大,模拟实际处理中对原始图像的插值放大步骤,最后利用本文算法计算出每张图中目标的角度并与真实角度相比较,取目标倾角0°~180°的所有图片为一组,将这一组图片的平均误差作为图中的角度误差值,实验结果如图6 所示,彩色效果见《计算机工程》官网HTML 版。从图6 可以看出,原图(尺寸缩放系数为1)的角度误差最小,随着尺寸缩放系数的变小,图像尺寸变小,角度误差增大。当原图按0.03 倍缩放后,图像中目标最窄处大约只有4 个像素宽,此时处于角度误差急剧增加的拐点附近。

图6 不同缩放与重构系数下的平均误差曲线Fig.6 Average error curves after different scaling and reconstruction coefficient
为了更清楚地显示不同重构系数插值对算法准确率的影响,取拐点处0.03 倍缩放的图片,按不同放大系数放大后进行角度测量,所得误差曲线如图7 所示。从图7 可以看出,随着放大系数的增大,误差逐渐减小,但过大的放大系数并不会使误差降低太多。为平衡计算量和误差,实际测量中取重构放大系数为5。

图7 原图按0.03倍缩放后在不同重构系数下的平均误差曲线Fig.7 Average error curve of the original image after scaling by 0.03 under different reconstruction coefficients
3.1.2 目标角度对测量精度的影响
利用目标图像测量目标在相机拍摄平面内投影的倾斜角度是目标在实际空间中角度测量的第一步,针对这一步的误差估计,本文制作不同角度的目标投影仿真图,以验证所提算法的测量精度。
首先,针对数据集原图进行倾角测量,算法测量精度如图8 中实线所示;随后,为了模拟远距离目标的低分辨率图像,通过尺度缩放得到尺寸为90×90 大小的图片,使得图片中目标宽度大约为4 像素,如图5(b)所示,这种极限情况出现在目标角度为5°、20°、40°和50°时。对图像进行缩小后,可以看出由于分辨率限制,目标边缘有很多的锯齿状干扰项,影响了原来轴对称目标在图像中的轴对称特性,导致在计算中心轴线时偏差一个像素就会产生较大误差。降采样后图像的误差曲线如图8 中虚线表示,可以看出,本文算法在原始高分辨率图像上的角度误差很小,平均误差是0.006°。在低分辨率情况下,图像对称性受到影响,而且边缘有锯齿状干扰,误差提高,平均误差是0.103°。从图8 可以看出,误差具有对称性,主要是因为不同角度生成的图片的像素分布不同。
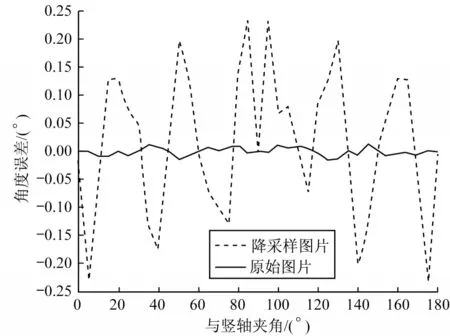
图8 原图和降采样图的角度误差对比Fig.8 Comparison of angle errors between original image and downsampling image
通过实验结果可以发现,5°以及对称位置上的85°、95°、175°处误差最大,误差绝对值均为0.233°。图片是按像素点离散保存的,会不可避免地存在抽样误差,在角度很接近水平或垂直时误差相对较大。但是,整体误差水平很小,在极限分辨率也即目标最细(只有4 像素)的情况下,误差也在0.233°以内。在精细测量情况中,需要尽可能地避免目标在图像中的角度处于垂直和水平附近,这样可以保证算法测量误差处于一个很小的范围内。
3.1.3 目标倾斜对测量精度的影响
不同目标物体的自身长宽比不同,且在飞行过程中目标存在画面外倾斜,导致目标在相机中的投影图像的长宽比存在很大变化,因此,本文制作不同长宽比的目标图像进行算法测量误差分析。因为目标角度为5°时位置误差最大,所以本次实验生成5°角度下长宽比分别为1.5~10(间隔0.5)的仿真图片,如图9 所示。

图9 不同长宽比的仿真图片Fig.9 Simulation images with different length-width ratio
本文算法在原始高清图、缩放后小图和按重构系数为5 重构放大后的仿真图上所得误差曲线如图10 所示。从图10 可以看出,随着目标长宽比的增加,角度误差降低。大的长宽比可以降低中轴线角度计算的误差,原始高清图片的误差最小,而在0.03倍缩放后,目标宽度只有约4 像素,测量误差相对较大。随着目标长宽比的增加,误差降低,缩小后的图片在经过比例为5 的重构放大后,相对未重构前,误差在小长宽比情况下降低明显。实验结果表明,本文算法在目标图像长宽比大于等于3 的情况下测量误差小于0.176°,通过重构可以减小边缘锯齿带来的影响,在大长宽比下可以更好地利用目标轴线方向上的信息,从而降低测量误差。

图10 不同目标长宽比下的误差曲线Fig.10 Error curves under different target length-width ratio
3.2 模拟验证
本文对飞行器的拍摄场景进行模拟。飞行器在低空飞行时,目标背景复杂[24],利用室外场景进行模拟;飞行器在高空飞行时,背景简单,利用室内布景的方式来模拟。实验过程如下:依据目标大小设置合理的拍摄距离,使得目标在相机图像中宽度大约为4 像素;抛出小物体,利用高速相机拍摄目标下落的过程,通过拍摄到的图像计算画面中的目标角度姿态,对比人工标定数据计算误差。
3.2.1 室外小目标角度计算
在室外场景中,所抛物体为水瓶,图像背景为远处的树木。图11(a)所示为截取的图像,目标最窄处只有4 像素宽,纹理信息全部丢失,只剩下轮廓信息。可以看出,图片中背景很复杂,非面积极大抑制法可以有效消除背景影响。图11(b)所示为对应的角度计算结果,从中可以看出,采用椭圆拟合的方法利用目标整体信息,尽可能地降低了目标边缘锯齿带来的误差,从而提高了目标的姿态角度测量精度。

图11 室外场景下目标姿态角度计算结果Fig.11 Calculation results of target attitude angle in outdoor scene
3.2.2 室内小目标角度计算
如图12(a)所示,在室内环境下,用高速相机拍摄笔帽自由落体时的姿态,测量结果如图12(b)所示。室内场景模拟目标在高空中的飞行过程,目标在高空中飞行时背景为天空,背景均匀,相对低空时背景干扰较小。
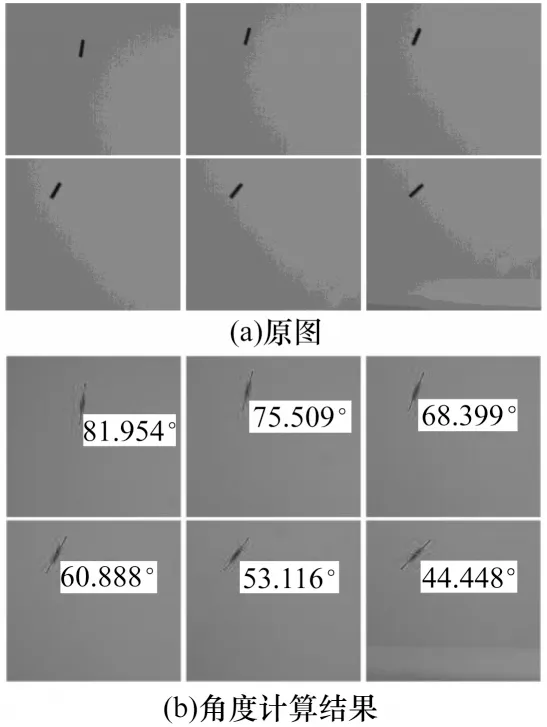
图12 室内场景下目标姿态角度计算结果Fig.12 Calculation results of target attitude angle in indoor scene
3.2.3 模拟结果分析
本文将所提利用目标整体信息的算法和利用目标轮廓信息的霍夫变换法进行精度分析与比较,其中,真值为人工标注的目标角度。2 种算法的误差对比结果如表1 所示。从表1 可以看出,在室外复杂背景情况下,由于图像中目标边缘不是完整的直线段,因此利用边缘信息的霍夫变换法的误差较本文算法大很多,霍夫变换法的相对误差最大为32.416%,绝对误差最大为1.984°,而本文算法的相对误差绝对值最大为9.208%,绝对误差最大为0.325°。在简单背景下,目标轮廓清晰,利用边缘信息的霍夫变换法绝对误差最大为0.787°,相对误差最大为1.298%,本文算法绝对误差最大为0.307°,相对误差最大为0.432%。本文算法在高复杂度和低复杂度情况下性能均优于只利用目标边缘信息的霍夫变换法,且绝对误差最大值均小于0.33°,算法稳定可靠。由于视觉差异,人工标注也存在一定浮动,因此,在误差允许范围内可以认为本文算法满足小目标角度测量的精度需求。

表1 2 种算法的测量误差对比Table 1 Comparison of measurement errors of two algorithms
4 结束语
在目标姿态测量的过程中,远距离、高速飞行的目标在相机中的成像纹理信息缺失从而导致传统光测方法使用受限的问题。为此,本文提出一种基于惯性椭圆拟合的姿态测量方法,以提取图像中丢失纹理信息的极小目标的中轴线倾角和中心点坐标。模拟实验结果表明,该方法在对目标处于高空和低空2 种不同状态下的姿态进行测量时均具有较高的精度,其可以实现导弹等小目标姿态的自动测量,降低人工判读的工作量。下一步将对多目标的自动跟踪与姿态识别以及非圆柱体形状目标的姿态识别问题进行研究。
