基于多普勒测速的水下传感器时间同步算法

姚宇婕，刘广钟，孔维全

（上海海事大学信息工程学院，上海 201306）

0 概述

海洋环境监测在科学勘探、商业开发和海岸保护等活动中的地位不断提升［1］，这种广泛监测的理想载体是一种分布式水下无线传感器系统，称为水下无线传感器网络（Underwater Wireless Sensor Network，UWSN）［2］。由于传感器的维护工作较为困难，且考虑到节点在长时间工作后，节点的本地时间与标准时间之间存在一定的偏差。而时间同步作为节点间协调与合作完成各项分布式任务的关键技术支撑，同时也是介质访问控制、路由转发和传感数据融合等［3］多项关键技术的基础。若多个节点的时间各不相同，则无法协同完成后续多项工作。在水下部署传感器节点的要求远高于陆地，这些节点一经部署基本不再进行维护和更换，因此水下传感器的计算资源与能量存储十分有限。水声信道的传播速度大约仅有1 500 m/s［4］，部分陆地传感器进行时间同步时通常忽略传播延迟，但是在水下环境中，巨大的传播延迟在节点通信时是不可忽略的重要因素。此外，受到海水的温度、盐度和密度等多种环境因素的影响［5］，水下声波的速度会发生较大的随机性变化，更为重要的是，传感器节点具有随洋流影响而移动的特点［6］，在某节点发送消息和接收回复消息的间隔中，由于传播延迟的存在，节点已发生了相对移动，因此，在设计水声传感器网络的时间同步算法中，须考虑到上述特性。

本文综合考虑水声通信中的各种特点，提出一种新型的基于多普勒测速的水下传感器时间同步算法。利用多普勒效应导致的频率变化［7］特征来构建整个WSN 网络的时间同步机制，并将分簇模型［8］作为水声传感器通信网络的样例，通过发送-接收双向的数据包交互方式得到自身的时钟相偏，以达到整个系统的时间同步。

1 相关工作

目前，针对陆地传感器的时间同步算法的研究成果有RBS［9］、TPSN［10］和FTSP［11］等。但是它们都没有考虑到海洋环境的特殊性，并且忽略传播延迟的存在。因此，该类协议并不适用于水下传感器。关于水下传感器时间同步的研究也取得了一些进展，如TSHL［12］是为水下环境而设计的时间同步协议，且将传播延迟纳入算法设计的考虑范围。该算法的运行过程分为2 个阶段，第一阶段是采用单向信息交互的方式组成25 个时间戳对时元组，并采用线性拟合法来估计本地时钟的时钟频偏。第二阶段是通过执行一次信息双向交互，以获得4 个重要的时间戳信息，并利用公式计算时钟相偏和传播延迟的大小，以对节点进行相应的补偿。这种算法并未考虑节点移动问题且假设传播延迟不变，不适用于实际情况。MU-Sync［13］利用分簇的思想减小节点移动性所带来的影响，簇首负责对簇内节点完成时间同步。该算法也可分为2 个阶段，在第一阶段中，使用发送-接收的双向报文交互收集4 个时间戳组成一个REF 参考信标组（共10 组），并执行2 次线性拟合操作。在第二阶段中，簇首节点将第二次拟合的估计值通过一次单向报文传输发送给待同步节点使其完成本地时钟校正。Mobi-sync［14］基于流体力学假设，利用空间相关性估计水下物体的移动速度。这种算法共分为传播延迟估计、线性拟合和校准阶段3 个阶段。Mobi-sync 相比前两种协议，同步精度得到明显提升，但所需计算量过于庞大，并且每个待同步节点的一跳传输范围内必须存在3 个以上的超级节点，因此需要预先在水下布置大量的超级节点，造成成本增加，实现过程较为困难。文献［15］提出一种多普勒辅助水下传感器网络时间同步机制，无线传感器通过接收到的超声波频率变化计算自身当前相对于浮标的移动速度及距离，并且所有无线传感器根据距离估计的结果来完成与浮标时间的同步校正。但是该算法存在一定的局限，一方面是只使用水面浮标对水下传感器节点进行距离估算时，其应用场景仅限于浅水区域，无法对深水区节点进行测量，且会造成一定的误差。另一方面是算法的计算量庞大，造成同步工作的效率较慢，无法快速对所有节点进行同步。针对这些问题，本文算法使用分簇思想进行改进，不仅使用水面浮标、水下传感器节点承担信标节点完成同步工作，加快同步进程，而且分簇还可缩短节点间的距离，提高同步精度。文献［16］提出利用多普勒效应辅助时间同步，由于节点在数据传输时发生运动，数据帧在多普勒频移的影响下将被压缩或扩展，因此接收信号的长度会发生变化，通过比较发送、接收数据帧的时间估计多普勒因子的值，进而获得节点的移动方向与速度，但方案中并未描述具体的节点间同步方法，且算法需要配备额外的测量器，增加了部署成本。本文算法明确了簇首同步和簇间同步2 个具体的实现过程，并规定了数据包的交互形式。

2 多普勒测速方法

多普勒效应是指波源和接收者之间由于相对运动使得接收者能够感受到波的频率变化，这是一种普遍的物理现象，在水下环境中尤为明显，且可广泛应用于医学、交通和航天等领域，并在定位和测速等技术上做出重大贡献［17］。基于多普勒效应造成的频移现象在频域上可表现为频率的变化，当一个移动的波源向接收者接近时，波会被压缩且波长变短，导致频率变得较高；反之，当波源远离接收者时，波会被拉伸，波长增加从而导致频率变得较低。该理论是由奥地利科学家克里斯琴·多普勒·约翰于1842 年提出的［18］。

假设波源S 和接收者E 在同一水平线上运动，假设f0为波源发出的初始信号频率，f为接收者收到信号时的实际频率，λ表示波长，v表示波速，波源的移动速度为vS，接收者的移动速度为vE，这3 种速度都具备方向性。接下来分为以下3 种情况讨论多普勒效应的存在方式。

1）当波源靠近接收者而接收者静止不动时，此时波速变为v-vS，其波长为，因此接收者得到的频率，且联立可得：

2）当波源静止而接收者靠近波源时，此时波源的波速为v+vE，波长仍然为λ，因此接收者观察到的频率，将代入可得：

3）当波源和接收者相向运动时，可由式（1）和式（2）求得接收者处的频率为：

3 浮标与簇首同步算法

3.1 浮标与簇首节点相对速度的计算方法

传感器随机分布在水下环境中，每个节点都有其各自的深度、位置和速度信息［19］。在水平面上放置多个均匀分布的浮标作为信标节点，其能量充足且带有GPS 定位功能，并且已完成时间同步，具有全球标准时间。浮标通过持续发出超声波与水下节点进行通信。时间同步的进程是传感器的簇首首先向浮标发起同步请求，浮标向簇首发送多段超声波，而簇首通过接收到的声波频率变化来估算其自身移动速度，从而计算精确的传播延迟。本节接下来将会详细说明移动速度的估算方法。

从观察浮标与簇首的位置情况可以发现，与波源移动而接收者静止不动的情况类似，即簇首移动而浮标静止不动。图1 直观表示了浮标与簇首节点交互情况［14］。其中A 为水面浮标，P 为待同步节点，节点的移动速度为V，浮标与节点之间连线的水平夹角为θ。浮标向待同步节点发送多段波速为u、频率为f0的超声波，并假设待同步节点接收声波时的频率为f1，则根据上节所述可得f0与f1之间的关系为：

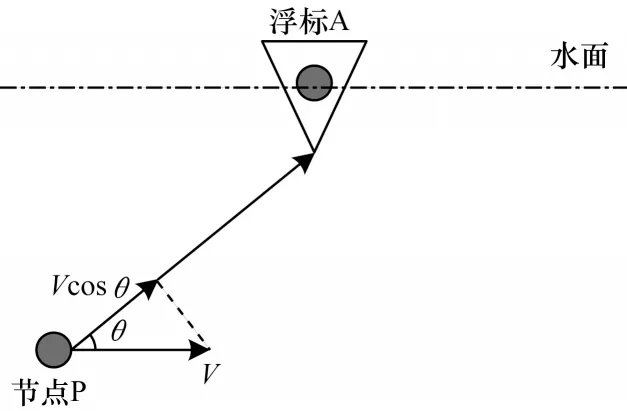
图1 浮标与簇首节点交互情况Fig.1 Interaction between buoy and cluster head node

浮标发送的多段超声波的初始频率都为f0，而待同步节点由于具有移动性，每次接收到的信号频率fi都会发生变化，则由式（4）可推导出式（5），当其他条件都可知时可求得节点的移动速度Vi。

3.2 信息交互过程

本节将介绍节点间的同步过程。根据时钟同步原理，待同步节点P 的本地时钟与标准时钟的关系为T=at+b，其中，t为标准时间，a表示时钟频偏，b表示时钟相偏［20］。根据上文所述，浮标与待同步簇首之间的报文交互如图2 所示。

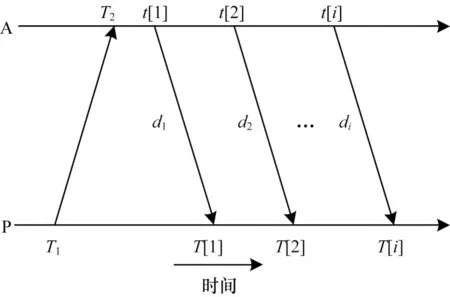
图2 浮标与待同步簇首之间的报文交互Fig.2 Message interaction between buoy and cluster head to be synchronized

节点P 在T1时刻向浮标发起同步进程，浮标A在T2时刻接收到消息后随即向待同步节点P 发送多段超声波，其时间戳用t[i]表示，P 接收到的信息时间戳用T[i]表示。当浮标A 首次发送同步信息，其发送时间为t[1]，经过时间d1后，信息到达待同步节点P，节点P 记录信息到达本地时间为T［1］。经过固定时间间隔后，浮标A 再次向节点P 发送第2 个同步信息，由于节点受到洋流等影响会发生移动且在传播过程中不可忽略，因此信息传播延迟已不是t1而是t2，则可得出：

假设浮标A 为水面上的固定装置没有移动性，待同步节点P 在水下的移动速度为V1，波速为u，则可以得出：

式（7）的意义是2 个节点在第2 次交互时的距离等于第1 次交互时的距离加上节点在传播过程中发生移动而产生的距离，且整理后可得：

其中，待同步节点P 的移动速度V1可由上节中描述的方法计算得出。将上述公式推广，则可得到每次信息交互的传播延迟与移速的关系为：

其中，i≥2。接下来联立由式（9）组成的方程组，通过消元法先消去b，并将式（10）代入可求出节点的时钟频偏为：

从算法描述可以看出，通过多次信息交互最终可求出i-1 组时钟频偏与时钟相偏，再将多次数据取均值作为最后时钟同步的补偿值。本节主要工作是完成浮标与簇首节点的时钟同步。

4 簇内节点同步算法

4.1 簇首与成员节点相对速度的计算方法

在簇首完成时间同步后可承担簇内的信标节点角色并向各成员节点发送时间同步消息。需要注意的是，此时簇首与其他节点都处于水面之下，将会受到洋流等因素产生移动。因此，在计算多普勒频移时需要使用2.1 节中描述的第3 种情况：波源和接收者都在移动。假设簇首为P，成员节点为B，簇首向待同步节点发送多段波速为u，频率为f0的超声波，并假设待同步节点接收声波时的频率为f1，簇首移动速度为VP，待同步节点移动速度为VM。，则可得出f0与f1之间的关系为：

由于在水中V＜＜c，因此上式可近似为：

当其他条件都可知时，易求得节点的移动速度为VP+VM。

4.2 信息交互过程

本节介绍簇首与簇内节点的同步过程。与第3 节不同的是，节点皆具有移动性，为了提高同步精度，本文采用混合的信息交换方式将时钟频偏与时钟相偏分开计算。如图3 所示，由待同步节点B 首先发起同步进程，然后簇首通过多次单向交互连续发送多段超声波至待同步节点，在此过程中计算时钟频偏，最后通过一组双向交互完成时钟相偏的计算。

图3 簇首与簇内节点的报文交互Fig.3 Message interaction between cluster head and nodes in the cluster

信息交互过程与第3 节所述类似，在此不再赘述。需要注意的是，P 和B 都具有移动性，则假设簇首P 的移动速度为VPi，待同步节点B 的移动速度为VBi，波速为u，则可推出：

式（15）的意义是2 个节点在第i次交互时的距离等于第i−1 次交互时的距离加上簇首与待同步节点在传播过程中分别发生移动而产生的距离。整理后可得：

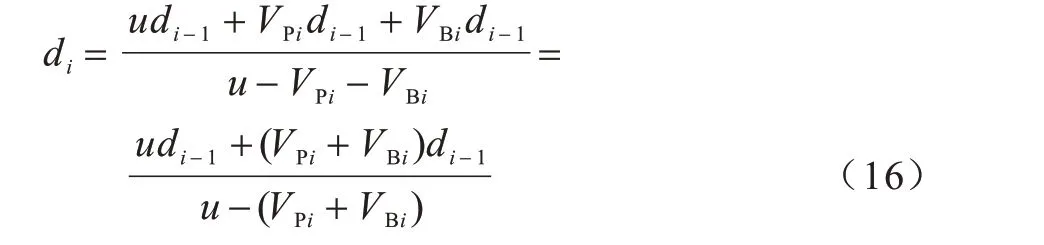
其中，VPi+VBi可由多普勒频率变化计算得出，而在得到传播延迟后，时钟频偏很容易得到。

在计算出时钟频偏后，待同步节点使用一次发送-接收的交互方式与簇首进行信息交换，完成对时钟相偏的计算，并收集如图3 所示的4 个时间Ta、Tb、

5 实验仿真

5.1 仿真参数设置

本文采用MATLAB 进行仿真，并在相同环境下比较本文算法与现有算法间的性能差异。本文仿真在1 000 m×1 000 m×500 m 的水下环境内进行，其中共有100 个水下传感器节点且为随机分布，浮标均匀分布在检测区域水面，且通信范围能覆盖所有传感器。节点运动通过多普勒辅助计算。仿真中使用的时间戳为MAC 层时间戳，其他实验参数如表1所示。

表1 仿真参数设置Table 1 Simulation parameter settings

5.2 实验结果及分析

普通节点在完成时间同步后，本文算法（CD-Sync）和MU-Sync、NU-Sync［20］算法的本地时钟误差增长趋势如图4 所示。从图4 可以看出，本文算法的误差累计明显小于其他2 种算法，在同步105s 后相比MU-Sync 和NU-Sync 减小了约68.27%和42.8%，在106s 后相比MU-Sync 和NU-Sync 减小了约44.56%和18.5%，而且随着时间的推移，误差呈倍数增加。本文算法同步误差小于其他算法，这是因为采用了分簇模型，缩小了节点间的距离且减少了传播延迟，并考虑了节点移动因素，进一步提高了精度。

图4 3 种算法簇内时间同步后的误差变化Fig.4 Error variation of three algorithms after intra cluster time synchronization

不同初始时钟频率偏斜对时钟偏差的影响如图5 所示。从图5 可以看出，时间同步完成10 s 后，普通节点计算本地时间与标准时间的差值，初始频率偏斜的变化范围为10−5～8×10−5，由于未同步算法No-Sync 没有对频率偏斜进任何行估计，因此时间误差的变化与不同的初始频率偏斜是呈接近线性递增关系。而Nu-sync 和本文算法CD-Sync 都对时钟频率偏斜进行了一定程度的估计，因此不同的初始频率偏斜对时钟偏差的影响都趋于稳定，但本文算法的误差略小于其他算法，可以体现出本文算法的性能更优。

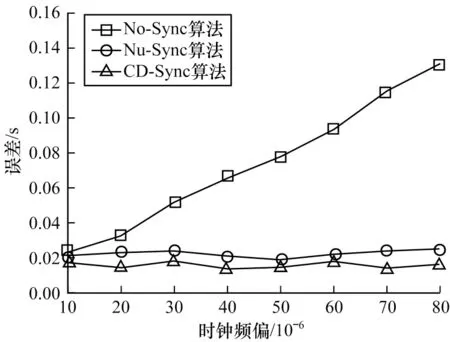
图5 初始时钟频偏对3 种算法误差的影响Fig.5 Effect of initial clock frequency offset on errors of three algorithms

传播延迟的动态变化主要是节点的移动速度导致的。节点的移动速度对4 种算法的同步误差影响如图6 所示。从图6 可以看出，三者的同步精度基本不受速度变化的影响，但是同步误差却有显著差别，MU-Sync 的误差主要在0.025 s 左右，NU-Sync 的误差主要在0.006 s 左右，而本文算法的误差均小于上述3 种算法。

图6 节点移动速度对4 种算法同步精度的影响Fig.6 Effect of node moving speed on the synchronization accuracy of four algorithms

在浮标与簇首、簇首与成员节点的同步过程中，充当信标的节点会向待同步节点发送多段同步信息，而同步信息的数量决定了时钟频偏的计算精度，图7 给出了3 种算法的不同信息数量与误差之间的关系。从图7 可以看出，随着信息数量的增加，3 种算法的误差都呈下降趋势，但本文算法的误差值更小。值得注意的是，当发送信息数量大于10 时，3 种算法的误差区域都趋于平稳。因此，从能量消耗的角度考虑，本文将发送的信息数量设置为10。

图7 4 种算法的数据包数量与误差的关系Fig.7 Relationship between the number of data packets and the error of the four algorithms

6 结束语

本文基于多普勒测速原理提出一种新型的时间同步算法。该算法使用最佳聚类的节能分簇模型将节点划分为簇首节点和簇内节点，簇首节点和水面信标节点利用多普勒效应进行时间同步，再将同步后的簇首节点与成员节点根据移动规律和多普勒效应进行时间同步，并利用多普勒原理估算节点间的相对移动速度，从而计算节点间的传播延迟。仿真结果表明，该算法可有效提高水下传感器传播信息的时间同步精度。下一步将利用距离最优原则选择最优簇头和簇密度，以进一步提高时间同步精度。