密集MANET 下MPR 的改进蚁群优化算法研究

赵启超，杨余旺，谢勇盛，汤小芳，李 操

（南京理工大学计算机科学与工程学院，南京 210094）

0 概述

移动自组网（Mobile Ad-hoc Network，MANet）是由一系列对等通信节点组成的分散式网络［1］，该网络无中心控制节点且节点间相互独立，旨在不依赖预先存在的基础架构下提供网络无线服务［2］。随着网络设备的不断增加，自组网已经延伸至各行各业，而人群的聚集与流动性通常给自组网带来巨大的挑战，密集型移动自组网中由于节点数目庞大且分组数量繁多，易导致网络拥塞甚至瘫痪，因此研究适用于密集流动型复杂场景的路由协议对于改善网络性能具有重要的意义。

优化链路状态（Optimized Link State Routing，OLSR）协议中多点中继（Multi-Point Relay，MPR）机制［3］有效抑制了消息开销，每个节点在接收到消息时都会重传消息，而MPR 机制中的消息仅由被选为MPR 的节点转发，实现了控制消息数量的优化，使得OLSR 协议在密集MANET 中具有很好的应用。传统的MPR 机制使用贪心算法，二跳节点覆盖数多的邻居被优先选为MPR，这导致MPR 集合存在较大冗余且网络越密集发生的概率越大。

蚁群优化（Ant Colony Optimization，ACO）算法［4］是一种来自于模仿蚂蚁觅食而得到的群体智能优化启发式算法［5-7］。该算法的优势在于其搜索的随机性，而传统贪心算法没有进行全局检测，仅限于当前最优。ACO 算法利用随机概率选择下一路径，但由于信息素和权值等因素的影响，导致某一路径的选择概率大幅增加，当概率增加到1 时，蚁群算法退化为传统贪心算法，将会陷入某一局部最优解。启发式蚁群算法在贪心算法基础上有所改进，但仍存在迭代时间过长而容易陷入局部最优解等缺陷［8-9］。针对MPR 贪心机制的局限性，本文结合ACO 算法的全局搜索能力对原有ACO 算法的路径选择以及状态更新机制进行改进，从而将该算法应用到MPR 问题中，达到优化MPR 求解集合的目的。

1 相关工作

为解决MPR 节点的高能耗问题，文献［10-11］提出一种基于剩余能量与可达性的计算方法，该方法对节点能量的消耗进行优化，但是存在对MPR 的求解精度欠佳的问题。与其不同的是，文献［12］在追求网络服务质量的前提下提出了Min-Max 算法，并通过最大信号范围选择MPR 节点，使得在MPR 集合求解准确率上有所改进。文献［13］利用原始算法的优势，并引入三跳邻居的本地数据库加入MPR 的附加决策函数，达到进一步优化MPR 的目的，但是由于三跳邻居被考虑入MPR 选择时会造成计算量成倍增大的问题。为提高密集MANET 下的MPR 计算速度，文献［14］利用一种协作式MPR 选择程序允许节点的选择过程独立于其邻居节点进行，该算法实质为节点的分布计算，并不能达到满意的结果。最小MPR 问题是一个NP 完全问题，可采用群体智能方法进行解决［15］。蚁群优化算法被引入MPR 问题进行求解［16］时取得了良好的效果，但其采用传统的状态更新机制在迭代速度与求解精度上尚有不足。

ACO 算法已应用于多种领域，目前已有很多研究人员针对不同问题对蚁群算法进行相应的改进，比如文献［17］将变异机制引入蚁群算法以改善迭代时间过长的缺陷。文献［18］提出一种自适应调整信息素的蚁群算法，有助于算法跳离局部最优解。文献［19］在处理资源受限的项目调度问题时，提出一种用两种信息素组合的综合评估方法，处理该问题时较其他算法具有更优的性能表现。文献［20］从蚁群数目方面着手，利用多个蚁群进行相对竞争求解，并将其用于车辆路径问题，可实现对多路线进行同步搜索，并有效降低局部最优概率。文献［21］利用目标地址泛洪负载信息的方法来模拟食物气味散发的过程，该方法可使得每个节点获得服务器与链路的最新信息，从而加快算法的迭代速度。文献［22］将ACO 算法应用于数据挖掘领域中，并提取出一种基于规则的分类器。该分类器使用一种基于蚂蚁的分类技术AntMiner+为蚁群提供了明确定义，且具有处理多类问题以及包括间隔规则的能力，改善了局部最优解的情况。基于此，文献［23］开发出包括基于ACO 的特征选择和数据分类的金融危机预测模型，以进一步优化局部最优解和改善分类性能。目前ACO 改进算法针对不同的目标，优化策略也随之变化，但实际上其改进策略可归结为对蚁群寻路算法以及状态更新机制的改进，多数寻路算法根据不同的应用场景，选取相应的启发参数来追求全局搜索能力与完善正反馈机制。对于状态更新机制，多数改进算法仅使用某种信息素更新规则，忽略了错误路径信息素的过度增长问题，从而导致算法迭代速度下降。

蚁群算法的群体智能特性使得其在各种优化问题上具有良好的应用，本文将蚁群优化算法与MPR选择问题相结合，并在ACO 算法基础上进行改进，提出基于状态信息的动态更新ACO（Dynamic Update ACO，DUACO）算法。利用源节点到其一跳与二跳邻居集合来构建路径，通过蚁群选路的形式进行MPR 节点的选择。考虑到MANET 中的节点移动性问题，在ACO 的路径选择概率基础上，本文将节点的移动性指标加入计算。此外，本文利用一种状态信息动态更新的规则，并引入补偿-惩罚机制用于相应地提升和抑制正确和错误节点的信息素增长。通过对比DUACO 算法、传统贪心算法和ACO 算法，验证DUACO 算法提高了收敛速度并解决蚁群算法易陷入局部最优的问题，且可有效改善MANET 网络性能。

2 MPR 问题描述

多点中继的原理是在转发广播数据包时减少重复转发的次数，它能够将真正转发数据分组的节点变为原所有转发节点的子集。每个节点都从自身的一跳邻居节点中选取出某些节点作为MPR 节点，该节点为其转发数据分组，可以看出MPR 节点的数量直接影响了数据分组转发的数量。因此MPR 节点的数量应尽可能地少，以达到减少数据包重传的目的。

OLSR 协议中传统的网络泛洪机制为MPR，每个节点都会定期地更新自身的MPR 集合。MPR 问题可被描述为：给定节点集合N1={N11，N12，…，N1m}，N2={N21，N22，…，N2n}，N1 为源节点的一跳邻居集合，N2 为源节点的二跳邻居集合。假设cover(N)为节点集N在N2 中的覆盖集，算法的目的是在保证cover(N)等于N2 的前提下，使得|N|最小，即：

3 传统MPR 算法

OLSR 协议中只有被选为MPR 的节点才具有转发消息的权利，其余节点对接收到的消息进行处理或丢弃操作，并不进行转发处理。因此，MPR 集合的大小很大程度上影响了网络的负载能力。MPR选择算法的具体步骤如下：

步骤1源节点的MPR 集合从源节点一跳邻居中转发意愿为WILL_ALWAYS 的节点所组成的集合中待选。

步骤2计算一跳邻居节点的度数，一个节点的度数是指该节点的对称邻居节点的数目，但不包括执行计算的源节点。

步骤3如果某个二跳邻居节点只能被某个一跳邻居所覆盖（对称链接关系），那么将该一跳邻居加入到MPR 集合中，并从二跳邻居集中去除那些可以被MPR 集合中节点覆盖掉的节点。

步骤4对于二跳邻居中被多个一跳邻居覆盖的节点，应该按照以下优先级进行考虑：

1）根据一跳邻居节点的转发意愿等级，等级高的优先加入。

2）等级相同的按照节点的可达性（在N2 中覆盖且未被MPR 集合覆盖的节点数目），可达性大的优先加入。

3）可达性相同的，节点度数较大的优先加入，否则，随机选取。

一种网络拓扑状态如图1 所示。针对源节点S，其一跳邻居节点为｛A，B，C，D，E，F｝，二跳邻居节点为｛1，2，3，4，5，6，7｝。根据OLSR 传统的贪心计算方法得到的一种MPR 集合为｛A，C，E，F｝，且最小MPR 集的大小为4，而实际上源节点S的最小MPR集合为｛B，D，F｝，该算法优点在于快速简单，但是步骤4 中根据节点的覆盖数目来确定MPR 节点容易带来集合冗余且无法得到最优解的问题。

图1 MPR 冗余网络拓扑状态示意图Fig.1 Schematic diagram of MPR redundant network topology status

4 改进MPR 算法

针对传统MPR 算法的不足之处，本节将给出改进蚁群优化算法并对该算法进行建模。DUACO 算法以减少MPR 集合冗余为目的，算法在每次迭代时，蚁群都需要根据信息素等多种信息计算得出需要移动的下一路径，当蚂蚁选择一条路径并移动后，该路径会被留下信息素，各路径上的信息素都会周期性的挥发，随着正反馈机制激励下某一路径上的信息素浓度不断增加，该路径最终被选为最优路径，即该节点被选入MPR 集合。因此，DUACO 算法的核心是路径选择概率以及信息素等状态更新的计算。

4.1 目标函数

针对OLSR 协议中的MPR 选择问题，令源节点的一跳邻居集合为N1，二跳邻居集合为N2，蚂蚁数目为n，MPRi∈{0，1}表示是否将N1i选入MPR 集合，则本文算法的目标函数可表示为：

该目标函数返回MPRi为1 的和的最小值，即被选入MPR 集合中N1 的最小个数，因此本文算法的目标是不断优化target 以使其取到最小值。算法开始时N1 中所有节点信息素被初始化为DEFAULT，记最大迭代次数为ITER_MAX，Q为N1 中所有信息素大于0 所组成的集合，即：

当集合Q中不存在冗余或是已经达到最大迭代次数时算法停止，此时最小MPR 即为Q：

4.2 路径选择概率计算

在MPR 的选择问题中，蚁群算法与传统算法的区别在于下一路径的选择不是绝对的，蚁群算法拥有全局探索能力，可以减少局部最优解的发生概率。蚂蚁在移动过程中，对于下一路径的选择取决于节点上的信息素、权值以及该节点的移动速度等多种因素，这里指该节点覆盖但不包括MPR 集合中覆盖N2 节点的个数。蚂蚁i对于下一城市j的选择概率公式可以表示为：

其中，μ(k)表示节点N1k上当前存留的信息素浓度，ν(k)表示节点N1k的权值，即该节点当前覆盖的二跳邻居个数，可将其定义为：

s(k)表示节点N1k移动速度对于概率选择的影响公式，且可定义为：

其中，speedN1k表示目标节点相较于自身的运动趋势，speedN1k＞0 时表示节点在向自身移动，节点速度越快该值越大，该节点作为MPR 节点的概率就会变大，反之该节点作为MPR 节点的概率将会随移动速度的增大而变小。

α表示信息素启发式因子，β表示权值启发式因子，γ表示移动速度启发式因子。其中，0 ＜α＜1，0 ＜β＜1，0 ＜γ＜1，α、β和γ值的大小反映了选取下一路径时节点的信息素、权值和移动速度的重要程度。在算法初期，各路径上信息素浓度初始相同，设置较大的β有利于加快算法的收敛速度，应注意到当β值接近于1 且α与γ值接近于0 时，该算法则退化成贪心算法。

4.3 状态更新计算

状态更新主要指对于节点上信息素残留的更新，为了使算法每次迭代结果更趋近于最小MPR 集合，并且防止算法出现停滞、局限于局部最优解等情况，信息素的更新过程是蚁群算法中极为关键的过程。为解决该问题，本文提出一种信息素以及全局最优解动态更新的方法，设置全局最优解集合为best 并全部初始化为0，besti=1 表示将城市i选入best 集合，蚂蚁一次迭代选择的解集合为res，resi=1表示蚂蚁将城市N1i选入res，其初始化全部为0，本文算法的状态更新规则如下：

1）全局最优解的更新过程，且更新规则如式（8）所示。

2）信息素更新有2 个过程，蚂蚁留下信息素与信息素的挥发过程，为了使本文算法避免出现局部最优的情况，根据蚂蚁每次迭代所选取的解与全局最优解集合进行动态地更新信息素的增加与减少数量。节点N1i上的信息素更新规则可被定义为如式（9）所示。

其中，ρ为信息素挥发剩余系数，0 ＜ρ＜1，ADD 为信息素增加常量，DECRE 为信息素挥发常量。信息素减少过程由系数ρ与DECRE 以及全局最优解集best确定，当best 趋近于最优解时，best 会变小且收过程将会得到加快。息素增加过程由ADD 以及当前解集res 确定，当res 过大时，则信息素增加会得到限制，可防止解的集中化并增加全局化节点搜索的概率，进而限制局部最优，而当res 变小趋近于最优解时，信息素增加幅度变大。

4.4 迭代优化机制

当全局最优解被更新时，为防止某个最优节点被选取时自身信息素过小的问题，本文亦增加了补偿机制，对于每次迭代，本文增加以下规则：

其中，θ为增幅因子，决定了补偿幅度。该规则可以很好地解决了某最优节点自身信息素过低而难以被选取的问题，保证了启发式蚁群算法的正反馈机制。

此外，考虑到蚁群算法可能会出现某个非MPR节点上的信息素浓度大概率被增大而导致算法迭代速度变慢，本文算法也引入了如下惩罚机制：

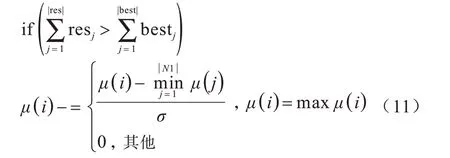
其中，σ为惩罚因子，当非MPR 节点上存在过高信息素浓度时，本文算法将根据此节点与当前节点中最小的信息素浓度计算得到惩罚信息素。

本文算法的补偿与惩罚机制主要取决于迭代结果res 的大小。若res ＞best，则说明MPR 节点被选中，该次迭代完成优化，采用补偿机制；若res ＜best，则说明非MPR 节点被选中，该次迭代可能趋于局部最优或延长迭代时间，即采用惩罚机制。

4.5 DUACO 算法步骤

利用源节点的二跳邻居拓扑来构建蚁群路径，每只蚂蚁从源节点出发，以达成N2 的全覆盖为目标，在N1 中计算出各路径的选择概率，将所选取的路径加入res 并更新res 对N2 中的覆盖节点，只有当N2 被已选的路径集合res 全覆盖时，该蚂蚁结束本次迭代，利用上述状态更新机制对信息素进行更新。算法设立最大迭代阈值为ITER_MAX，令Q为N1 中所有μ(i) ＞0 节点组成的集合。当迭代次数超过ITER_MAX 或者集合Q不存在冗余时，算法结束迭代，此时集合Q或者best 即为最小MPR 集合。本文算法的具体步骤如下所示：

算法最终目标target 为|best|，所求出的最小MPR集合为best。

5 仿真及结果分析

为了验证本文算法的可行性，实验在仿真平台NS3上进行，采用NS3中OLSR协议并将DUACO算法加入到其MPR选择过程中，在不同网络密集程度下比较了默认MPR算法、蚁群优化算法以及DUACO算法的性能。实验选取仿真区域为1 km2，每个节点都采用NS3自带的随机运动-停止模型、节点位置以及移动速度随机生成。多次实验后得到性能稳定性最佳的参数如表1所示。

表1 实验参数设置Table 1 Experimental parameter settings

为研究本文算法对于网络性能的变化情况，实验给出了不同网络密度下3 种算法的网络性能对比，结果如表2 所示。从表2 可以看出，当节点数目较低时，网络拓扑稀疏，节点分散且存在孤立节点的概率较大，而通信距离有限，网络性能较差。随着节点数目的增多，网络性能得到改善，而当节点数目过多时，网络分组数目巨大且网络拥塞的概率变高，造成网络性能再度降低。

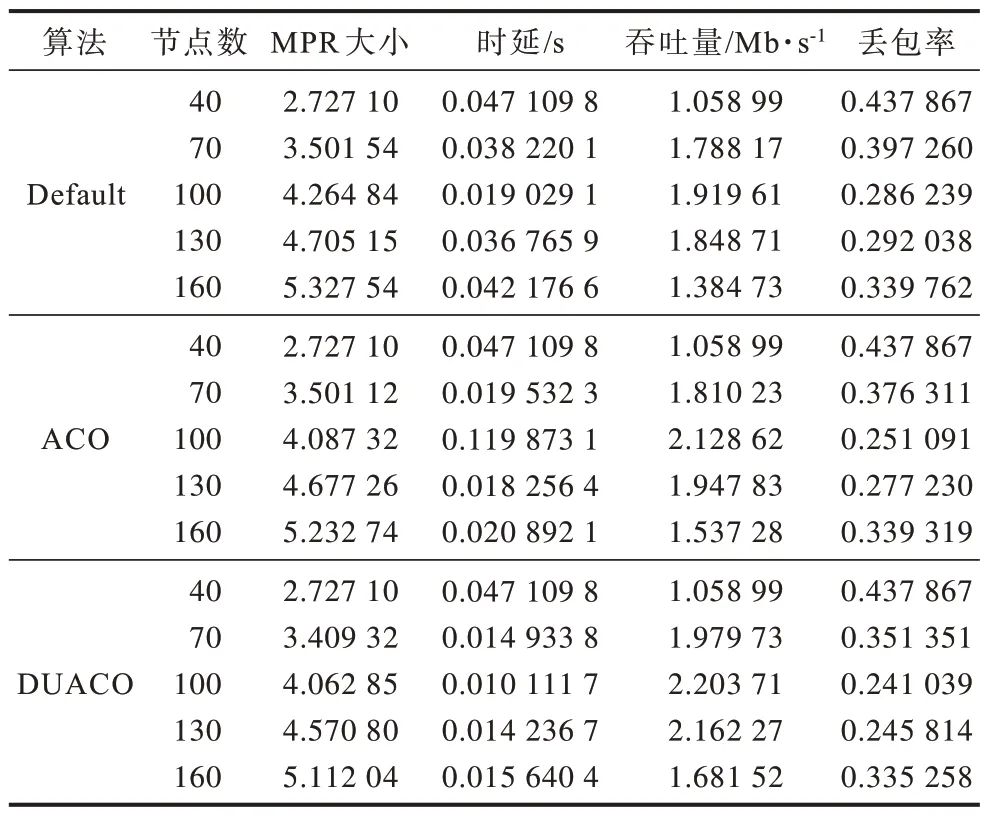
表2 3 种算法的性能对比Table 2 Performance comparison of three algorithms

当网络较为稀疏时，节点的一跳邻居集合较小，发生MPR 选取冗余的概率较小，因此当节点数目过低时，Default、ACO 和DUACO 算法通常性能差异性不大。此时ACO 和DUACO 算法使用较大的权值启发式因子，算法趋于传统贪心算法以求加快迭代速度，而随着节点数目的增加，ACO 和DUACO 算法逐渐加大信息素启发式因子的大小，以保证路径选择时的随机性，防止陷入局部最优。蚁群优化算法根据信息素以及权值确定状态转移概率，这种算法仅适用于固定的网络拓扑，当节点具有移动性且网络拓扑不断变化时，该算法不能取得预期的效果。

图2 给出了在不同数目节点下，ACO 与DUACO 算法的平均迭代次数对比结果。从图2 可以看出，DUACO 算法的状态信息动态更新机制有效加快了蚁群优化算法的迭代速度，迭代次数平均降低了8.531 61%，随着网络拓扑愈加密集，DUACO 算法的加快迭代速度愈加明显，当节点数目为160 时，ACO 算法达到最大迭代次数。从表2也可以看出，DUACO 算法相较于ACO 算法时延降低了40.565 8%，MPR 集合的大小减少了1.950 86%，网络丢包率降低5.791 26%，网络吞吐量提高了6.316%。

图2 ACO 算法与DUACO 算法的平均迭代次数对比Fig.2 Comparison of the average number of iterations between ACO algorithm and DUACO algorithm

为了研究Default、ACO 和DUACO 这3 种算法的能耗关系，实验测试了应用不同MPR 算法时节点执行时长与仿真进度之间的关系，结果如图3 所示。从图3 可以看出，DUACO 算法在速度上不及默认Default 算法，但相较于ACO 算法节点计算时长呈降低的趋势，这是因为本文在DUACO 重新定义了信息素的更新机制，加快了算法的迭代速度。另外，考虑到某些最优节点上信息素浓度过低难以被选取和非最优节点信息素浓度过高的问题，本文利用引入信息素补偿-惩罚机制来降低DUACO 陷入局部最优的概率，从而减少MPR 集合的冗余，对于网络性能的改善均优于ACO 算法与默认Default 算法。

图3 3 种算法的节点计算时间与模拟时间的关系Fig.3 The relationship between the node computation time and simulation time of the three algorithms

6 结束语

针对OLSR 协议中贪心MPR 机制的求解冗余问题，本文将蚁群优化算法应用到MPR 选择机制中，并在蚁群优化算法基础上加入了状态信息的动态更新以及补偿-惩罚机制。实验结果表明，利用ACO 算法求解MPR 问题时，在正确求解MPR 最小集的前提下，该算法可有效提高收敛速度和网络性能。蚁群优化算法受限于启发参数的选取以及影响因子的设置，对其进行合理设置具有很强的经验性。下一步将利用深度学习技术分析迭代过程中状态信息的变化情况，并根据冗余等数据信息自学习得到最优启发参数和影响因子，以进一步提升蚁群优化算法的迭代速度和求解精度。