基于群组与密度的轨迹聚类算法

俞庆英，赵亚军，叶梓彤，胡 凡，夏 芸

（1.安徽师范大学计算机与信息学院，安徽芜湖 241002；2.安徽师范大学网络与信息安全安徽省重点实验室，安徽芜湖 241002）

0 概述

随着定位、通信和存储技术的快速发展，车辆行驶轨迹数据、用户活动轨迹数据以及飓风轨迹数据等大量移动对象的轨迹数据可被搜集和存储。轨迹数据中包含丰富的时空语义信息，从中可挖掘出众多有价值的信息［1-2］。聚类分析是常用的数据挖掘方法，其被广泛用于图像分析［3］、模式识别［4］、知识发现［5］以及生物信息学［6］等领域。近年来，研究人员针对不同的应用领域提出多种聚类算法，主要包括以BIRCH 为代表的基于层次的聚类算法［7］、以STING为代表的基于网格的聚类算法［8］、以K-means 为代表的基于划分的聚类算法［9-10］，以及以DBSCAN 为代表的基于密度的聚类算法［11-12］。然而上述算法主要用于点数据的聚类，不能直接用于轨迹数据的聚类。

对轨迹数据聚类可获得移动对象的代表性路径，从而掌握其周期性行为规律［13］。由于轨迹数据中包含大量时间、空间和形状等固有特征信息，因此大部分轨迹聚类方法先进行基于轨迹数据对象的相似性度量，再通过改进传统聚类算法来实现轨迹数据聚类。例如，目前使用最广泛的TRACLUS［14］轨迹聚类算法先基于轨迹分段进行相似性度量，再利用传统DBSCAN 算法实现轨迹聚类。DBSCAN 算法可形成任意形状的簇并能有效处理噪声点，但由于该算法在执行过程中会重复遍历整个数据集来搜索某个样本的邻域集合，因此处理大数据集的耗时较长，时间复杂度为O（n2），并需要较大内存和I/O 开销。针对该问题，研究人员采用R-树［15］、KD-树［16］等空间索引方法降低邻域集合搜索所需计算次数来减少算法的时间开销，但空间索引方法实现较困难，且不适用于高维数据集。

针对上述问题，本文提出一种基于改进邻域搜索技术的聚类算法。对轨迹进行分段预处理找出具有较高相似度的子轨迹段，通过遍历整个轨迹数据集将其分为不同的群组，采用群组搜索代替距离计算减少邻域对象搜索的计算次数，以缩短算法在海量轨迹数据集上的运行时间。

1 相关工作

本文以TRACLUS 算法中相似性度量方法为基础，通过改进DBSCAN 算法来实现轨迹聚类，以下对DBSCAN 算法的相关工作进行介绍。

DBSCAN 算法是一种基于密度的空间聚类算法，其本质是寻找密度相连点的最大集合，能有效滤除低密度点区域，将高密度区域划分为簇，并在具有噪声点的数据中发现任意形状的簇。研究人员基于DBSCAN 算法的上述特性，对其不断改进与创新，并将研究成果应用于多个领域。

DBSCAN 算法需要人为确定半径参数ε和邻域密度阈值MinPts，这两个参数能否合理选取对聚类结果影响较大，然而目前DBSCAN 算法无法在多密度情况下设置参数。对此，文献［17］提出一种初始点优化与参数自适应的改进DBSCAN 算法，其能为不同密度的簇自适应设置不同参数，并优先对高密度簇进行聚类，即实现对多密度数据集的聚类。文献［18］通过改进DBSCAN 算法得到EXDBSCAN 聚类算法，可用于多密度数据集且只需输入一个参数。文献［19］结合DBSCAN 算法和粒子群算法提出改进算法，其可基于数据集自动生成参数并有效进行空间热点识别。

将DBSCAN 算法及其改进算法应用于轨迹数据集的处理也是研究热点之一。由于大部分轨迹数据集规模庞大且数据量丰富，因此提高DBSCAN 算法的计算效率非常重要。文献［20］提出一种可用于多密度数据集的RNN-DBSCAN 聚类算法，利用逆邻域计数和权值剪枝方法使算法的时间复杂度由O（n2）降为O（n）。文献［21］开发出DBSCAN 算法的分布式应用，在不影响聚类效果的情况下，使该算法在大规模数据集上实用性更强。文献［22］在提高DBSCAN 算法实时性的基础上，使用KD-树和Spark GraphX 分布式图处理框架，能显著减少数据集中样本之间距离的计算量，在大规模数据集上耗时更短。文献［23］结合MapReduce 分布式计算框架和Hadoop 平台，有效提高DBSCAN 算法在大规模数据集上的运行效率。文献［24］提出一种用于处理时空轨迹数据的HDBSCAN 算法，其考虑到传统聚类算法未考虑的轨迹先后性和内在层次，所得聚类结果更合理。文献［25］提出一种基于轨迹数据密度分区的分布式并行聚类算法，构建可分布式并行聚类的局部数据集，在不同服务器上执行DBSCAN 算法进行局部聚类，然后对聚类结果进行合并和整合，通过并行处理提高了聚类分析效率。

在上述基于DBSCAN 的改进算法中，分布式图处理框架和KD-树等空间索引方法均较难实现，且空间索引树较难应用于高维轨迹数据集。为此，本文提出一种基于群组和密度的轨迹聚类算法TraG-DBSCAN，以DBSCAN 算法为基础，使用群组划分方法减少聚类算法中邻域对象搜索所需时间，从而提高算法实时性，并利用邻域相似性度量提升轨迹聚类准确性。

2 本文算法

2.1 相关定义与符号

定义1（轨迹距离）轨迹距离是评价轨迹样本之间相似性的度量值，是轨迹聚类效果的重要指标之一。两个轨迹样本之间距离越大，其相似度越小，反之亦然。

本文采用文献［14］中的距离计算方法实现轨迹段之间的相似性度量，如图1 所示。

图1 距离计算示意图Fig.1 Schematic diagram of distance calculation

在图1 中，两个轨迹段trai和traj之间的距离dist(trai，traj)包含垂直距离d⊥、平行距离d∥和角度距离dθ3 个部分，相关计算公式如下：

其中，w⊥、w∥和wθ分别为d⊥、d∥和dθ的权重，在本文中均设置为1/3。

定义2（群组）群组是一条核心轨迹和若干条非核心轨迹组成的集合，核心轨迹与任意非核心轨迹之间距离不大于距离阈值ε。群组形状与最大半径为ε的圆类似。

定义3（边界距离）边界距离Ts和Tw分别为群组中s和w的核心轨迹到非核心轨迹的最大距离，其值不大于ε。

定义4（群组可达）设Cs和Cw分别为不同群组s和w的核心轨迹，当满足‖Cs-Cw‖≤Ts+Tw+ε时，称s和w为群组可达，群组si的可达群组集合记为R(si)。

2.2 算法框架

在对轨迹数据集中一条轨迹进行聚类时，通常会忽略部分具有较高相似度的子轨迹段。因此，本文在对轨迹数据集聚类前，根据信息学中最小描述长度（Minimum Description Length，MDL）［14］原则对轨迹进行分段预处理。假设一条轨迹TRi=p1p2…pleni，特征点集合points={p1，p2，…，pleni}，计算公式如下：

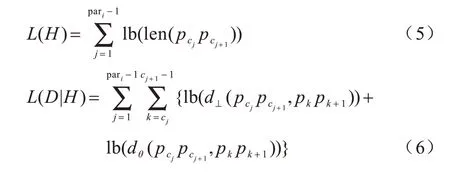
其中，len(pcj pcj+1)为两点之间的欧几里得距离，d⊥和dθ分别由式（1）和式（3）计算得到。

图2 为TraG-DBSCAN 算法流程，该算法包括两个阶段：1）通过2 次遍历轨迹数据集获得基于子轨迹段的群组集合；2）对子轨迹段进行聚类，并利用群组集合减少聚类算法中搜索轨迹样本邻域集合所需时间。

图2 TraG-DBSCAN 算法流程Fig.2 Procedure of TraG-DBSCAN algorithm

2.3 群组的建立

在群组建立阶段，通过2 次遍历整个轨迹数据集将其划分为不同群组，符合相应条件的群组之间相互可达。

1）在第1 次遍历轨迹数据集时，对于每个轨迹样本，若群组数为0 或不存在任意一个群组的核心轨迹与该轨迹样本之间距离不大于2ε，则以该轨迹样本为核心轨迹建立新群组；若存在一个群组的核心轨迹与该轨迹样本之间距离不大于ε，则将该轨迹样本划分到此群组中；若上述两种情况均不符合，则将该轨迹样本标记为未处理轨迹，等待进行第2 次遍历过程。

2）在第2次遍历轨迹数据集时，对于每个在第1次遍历中被标记为未处理的轨迹样本，计算其与所产生群组中核心轨迹之间的距离。若存在一条核心轨迹与该轨迹样本的距离不大于ε，则将该轨迹样本划分到相应群组；否则以该轨迹样本为核心轨迹建立新群组。

值得注意的是，以不同顺序处理轨迹样本会产生不同群组，但并不影响最终聚类结果。当一个新轨迹样本加入群组时，群组的边界距离需进行更新。通过计算两个群组中核心轨迹之间的距离可判断群组之间是否可相互抵达，当两者之间距离不大于两个群组的边界距离与ε之和时，这两个群组为可相互抵达。由于群组的边界距离在算法结束前才可确定，边界距离取最大值ε作为替代值，因此当两条核心轨迹之间距离不大于3ε时，这两个群组可相互抵达。以下分别为建立群组算法Group和CreateGroups（S，tra）函数算法的伪代码。

算法1建立群组算法Group

算法2CreateGroups（S，tra）函数算法

2.4 轨迹聚类

TraG-DBSCAN 算法中的轨迹聚类算法以传统DBSCAN 算法为基础，采用群组搜索方法代替距离计算方法，以减少搜索邻域集合所需计算次数和算法在规模较大的轨迹数据集上的时间开销。

2.4.1 改进的邻域搜索算法

在传统DBSCAN 算法中，搜索邻域集合主要通过计算该样本与数据集中其他样本之间的距离来实现，其在大规模轨迹数据集上时间开销较大，建立群组可减少搜索邻域集合所需计算次数。在搜索轨迹样本时，首先判断该样本所在群组的边界距离，若边界距离不大于ε2，则该群组中所有样本都处于该样本的邻域内，否则再分别计算；若边界距离在（ε2，ε）范围内，则将样本添加至邻域内。然后选取该群组的可抵达群组中的样本。邻域搜索算法FindNeighbours 的伪代码见算法3。

算法3邻域搜索算法FindNeighbours

2.4.2 轨迹聚类算法

基于上述邻域搜索算法进行轨迹聚类，以下分别为轨迹聚类算法ClusterTra 和ExpandCluster（Q，C，ε，MinPts，S）函数算法的伪代码。

算法4轨迹聚类算法ClusterTra

算法5ExpandCluster（Q，C，ε，MinPts，S）函数算法

2.5 时间复杂度

TraG-DBSCAN算法的时间复杂度包含以下3个部分：

1）轨迹分段处理的时间复杂度。遍历整个数据集，处理每条轨迹并获得待处理的子轨迹段，此部分时间复杂度为O（n）。

2）基于子轨迹段建立群组的时间复杂度。遍历整个子轨迹段集合进行群组初步划分，未被划分到任何群组的子轨迹段在第2 次遍历中进行处理。假设p为最初群组划分后剩余的子轨迹段数目，则基于子轨迹段建立群组的时间复杂度为O（n+p），由于p≪n，因此该部分时间复杂度也为O（n）。

3）基于划分的群组对子轨迹段进行聚类的时间复杂度。该部分耗时主要集中在对每个子轨迹段的邻域搜索上。在对子轨迹段样本进行邻域集合搜索时，需计算该样本与所有可达群组中全部轨迹段样本之间的距离，以及该样本与数据集中所有其他轨迹样本的距离。如果未做任何改进，则该部分的时间复杂度为O（n2）。实际上，TraG-DBSCAN 算法在该部分做了相应改进，需计算子轨迹段样本与可达群组中轨迹样本之间距离。此外，对于待处理的子轨迹段样本，算法会对该样本的可达群组进行相应的剪枝处理，从而减少时间开销。假设d为数据集中邻域集合搜索所需最大计算次数，则聚类阶段的时间复杂度为O（nd）。

综上所述，TraG-DBSCAN 算法的时间复杂度为上述各部分时间复杂度之和O（n）+O（n）+O（nd），其总体时间复杂度为O（nd）。对于可行的邻域参数ε，d通常很小且受到样本对象处理顺序的影响。

3 实验与结果分析

本文在不同轨迹数据集上验证TraG-DBSCAN 算法（以下称为本文算法）的有效性和准确性，将本文算法与TRACLUS 算法的运行时间和聚类结果准确性进行对比分析。本文算法和TRACLUS 算法均由Matlab语言实现，实验环境为AMD FX-7600P Radeon R7 4 核处理器，8 GB 内存，Windows 7 操作系统以及Matlab 2016b 运行平台。

3.1 实验数据集

本文实验采用Best Track大西洋飓风轨迹数据集，其记录了大西洋飓风发生的时间、经纬度、最大持续风速和每6小时的中心气压。本文从该轨迹集中选取飓风发生的时间和经纬度轨迹数据进行实验。每条轨迹数据的存储格式T={Tid，loc1，loc2，…，locn}，其中Tid为轨迹标识符，loci=＜ti，lati，longi＞(i=1，2，…，n)为每个时刻的位置点，其中包含时间、纬度和经度信息。将1990 年至2013 年的大西洋飓风轨迹数据作为数据集DS1，该数据集包含152 条飓风轨迹，共6 557 个轨迹点。将1851 年至2013 年的大西洋飓风轨迹数据作为数据集DS2，该数据集包含855 条飓风轨迹，共30 146个轨迹点。

3.2 评价指标

3.2.1 轮廓系数

本文采用以下轮廓系数评价算法的聚类效果：

1）计算样本i到同簇中其他样本的平均距离a（i），该值越小说明样本i更应被聚类到该簇。将a（i）称为样本i的簇内不相似度。

2）计算样本i到其他某簇Cj中所有样本的平均距离bij，将min{bi1，bi2，…，bik}（k为其他簇的个数）定义为样本i的簇间不相似度，记为b（i）。

3）样本i的轮廓系数值记为s（i）并定义如下：

其中，若s（i）接近1 则说明样本i聚类更合理，若s（i）接近−1则说明样本i更应分类到另外的簇，若s（i）近似为0则说明样本i在两个簇的边界上。

3.2.2 总平方误差和

为进一步验证本文算法的可行性，采用总平方误差和（Total Sum of Squared Error，TSSE）作为算法聚类效果的评价指标，其计算公式如下：

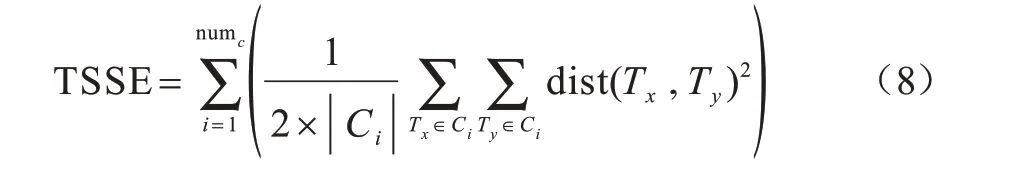
其中，numc表示簇的个数，|Ci|表示第i个簇中轨迹样本的个数，dist（Tx，Ty）表示轨迹样本Tx和Ty之间的距离。TSSE值越小，算法聚类效果越好。

3.3 参数设置

人为选取的半径参数和邻域密度阈值通常不准确，需耗费较多时间确定合适的参数值。本文在参数设置上避免人为干预，采用启发式搜索方法［14］确定ε，再通过最佳的ε确定MinPts，相关计算公式如下：

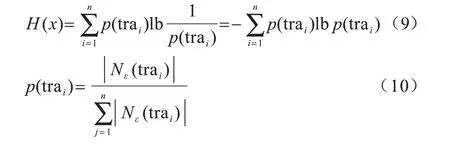
其中,Nε(trai)为轨迹样本trai的邻域集合,|Nε(trai)|为trai邻域集合中的轨迹样本个数。

由式（9）和式（10）可确定使H（x）最小的半径参数，即最佳半径参数ε。在此基础上，计算数据集的邻域轨迹样本数的平均值avg|Nε(trai)|，MinPts 的取值范围为[。

3.4 结果分析

3.4.1 运行时间的对比

表1 和表2 分别为不同半径参数和邻域密度阈值下本文算法和TRACLUS 算法在DS1 数据集上的运行时间。可以看出，2 种算法的运行时间均随着参数值变化而改变，本文算法在数据集DS1 上的运行时间远短于TRACLUS 算法。

表1 不同ε 值下2 种算法在DS1 数据集上的运行时间Table 1 Running time of two algorithms on DS1 dataset with different ε valuess

表2 不同MinPts值下2种算法在DS1数据集上的运行时间Table 2 Running time of two algorithms on DS1 dataset with different MinPts valuess

表3 和表4 分别为在不同半径参数和邻域密度阈值下本文算法和TRACLUS 算法在DS2 数据集上的运行时间。可以看出，在规模较大的轨迹数据集上进行聚类时2 种算法的运行时间均较长，本文算法在数据集DS2 上的运行时间远短于TRACLUS 算法，其在不同参数下时间开销更少。

表3 不同ε 值下2 种算法在DS2 数据集上的运行时间Table 3 Running time of two algorithms on DS2 dataset with different ε valuesh

表4 不同MinPts值下2种算法在DS2数据集上的运行时间Table 4 Running time of two algorithms on DS2 dataset with different MinPts valuesh

由上述分析结果可知，本文算法在DS2数据集上运行时间较TRACLUS算法的减幅比DS1数据集更显著。由此可知，本文算法可有效地应用于海量的轨迹数据集。

3.4.2 聚类结果准确性的对比

图3 为不同半径参数和不同邻域密度阈值下本文算法和TRACLUS 算法在DS1 数据集上聚类结果的TSSE 值对比情况。可以看出，本文算法的TSSE 值较TRACLUS算法更小，其在DS1数据集上聚类效果更好。

图3 2 种算法在DS1 数据集上聚类结果的TSSE 值对比Fig.3 Comparison of TSSE values of clustering results of two algorithms on DS1 dataset

图4 为不同半径参数和不同邻域密度阈值下本文算法和TRACLUS 算法在DS1 数据集上聚类结果的轮廓系数值对比情况。可以看出，本文算法的轮廓系数值较TRACLUS 算法更接近1，表明其在DS1数据集上聚类结果更准确。

图4 2 种算法在DS1 数据集上聚类结果的轮廓系数值对比Fig.4 Comparison of silhouette coefficient values of clustering results of two algorithms on DS1 dataset

图5 和图6 分别为不同半径参数和不同邻域密度阈值下本文算法和TRACLUS 算法在DS2 数据集上聚类结果的TSSE 值和轮廓系数值对比情况。可以看出，2 种算法的TSSE 值和轮廓系数值随着半径参数和不同邻域密度阈值的变化相应改变，本文算法的聚类评价结果较TRACLUS 算法更优。

图5 2 种算法在DS2 数据集上聚类结果的TSSE 值对比Fig.5 Comparison of TSSE values of clustering results of two algorithms on DS2 dataset

图6 2 种算法在DS2 数据集上聚类结果的轮廓系数值对比Fig.6 Comparison of silhouette coefficient values of clustering results of two algorithms on DS2 dataset

3.4.3 聚类结果的可视化

由上述对聚类结果准确性分析可知，在DS1 数据集上，当ε=281 且MinPts=10 时，本文算法聚类效果最好，选择该条件下的聚类结果进行可视化显示。类似地，在DS2 数据集上，当ε=190 且MinPts=17 时，本文算法聚类效果也最好，选择该条件下的聚类结果进行可视化显示。图7 和图8 分别为本文算法在DS1 数据集和DS2 数据集上的可视化聚类结果（彩色效果参见《计算机工程》官网HTML 版）。

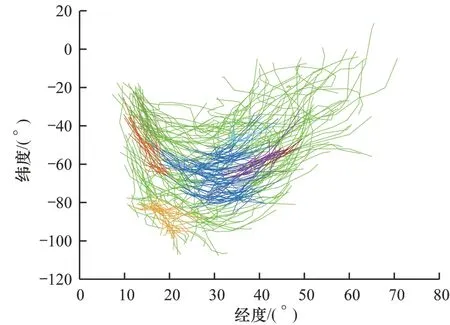
图7 本文算法在DS1 数据集上的可视化聚类结果Fig.7 Visual clustering results of the proposed algorithm on DS1 dataset

图8 本文算法在DS2 数据集上的可视化聚类结果Fig.8 Visual clustering results of the proposed algorithm on DS2 dataset

4 结束语

本文提出一种结合群组和密度的聚类算法。根据MDL 原则将一整条轨迹划分为若干条轨迹段，通过遍历轨迹数据集将所有轨迹段划分到相应的群组中，以减少聚类时邻域集合搜索过程中冗余的计算次数，最终利用群组和密度对轨迹数据集进行聚类。实验结果表明，与基于密度的TRACLUS 算法相比，该算法运行时间更短且聚类准确性更高，运行时间的减幅随轨迹数据集规模的扩大而增加。后续将结合并行和分布式计算框架，进一步缩短该算法在海量轨迹数据集上的运行时间并提升聚类准确性。