基于梁格法的大曲率箱梁桥力学特性研究

兰志昆

(中铁上海设计院集团有限公司长沙设计院 长沙 410018)

随着城市交通的发展，位于曲线段的匝道桥越来越多，已成为城市道路路网中不可或缺的立交桥型之一。不同于直线段桥梁，曲线段的匝道桥将存在“弯扭耦合”效应，造成力学性能复杂[1]。当曲率越大、圆心角越大、桥面越宽，“弯扭耦合”效应越明显，同时曲线桥的支点反力存在内外不均的分布特点[2-3]。

大曲率箱梁桥通常指曲线半径小于、等于100 m的箱梁桥。随着曲率半径的减小，大曲率箱梁桥的受力性能变得越来越复杂，传统设计方法以建立单梁模型为主，无法较为准确地得出结构内力及支反力，存在一定的设计安全风险。Hambly提出了剪力柔性梁格法，用一个等效的梁格体系来替代曲线梁桥的上部结构，不仅能够很好地模拟原结构的空间受力性能，还能处理各种不规则的支承形式、横梁作用，适用于各类弯梁桥分析[4]。

本文以某工程匝道大曲率箱梁桥为背景，上部结构进行单梁、梁格2种模型条件下的计算分析，然后以梁格建模分析结构在不同曲率半径、桥宽、跨径、支承形式等参数变化下的力学特性。

1 工程概况及有限元模型计算分析

1.1 工程概况

某立交匝道工程新建大曲率箱形梁桥，该桥位于大曲率半径R=40 m的曲线段，孔跨布置为3×16 m钢筋混凝土连续梁，单向双车道，桥宽10 m，各支点均采用双支承形式，平面布置见图1。曲线内侧P3为固定支承点，P1、P4、P5、P7为单向活动支承点，P2、P6、P8为双向活动支承点。主梁截面为单箱双室，斜腹板，梁高1.4 m，标准横断面见图2。靠近支点处顶底板、腹板加宽，各支点设置横梁，跨中设置横隔板。

图1 桥跨平面图(单位：m)

图2 标准横断面(单位：cm)

2 有限元模型

采用midas Civil建立上部结构单梁、梁格模型，其中端横梁、中横梁、横隔板以集中荷载形式施加于单梁模型，桥面铺装、防撞护栏以梁单元荷载形式施加于2个模型上。定义恒载为结构自重与上述荷载之和，下述分析均为基于恒载作用下的计算结果。

为保证梁格单元划分精度、平衡工程设计计算耗时，梁格划分遵循以下基本原则[5]。

1) 纵向构件的位置与纵向腹板相重合。

2) 横向构件与横隔梁、横梁重心重合，且增设的横向虚拟梁格间距不超过反弯点之间距离的1/4。

3) 各纵向单元顶底板的纵向划分位置尽量使得各单元截面的中性轴在同一水平面。

4) 弯梁桥在支承附近、内力变化较大的地方进行梁格加密。

5) 纵向构件单元划分所对应的圆心角不超过5°。

梁格截面划分为3片梁，分别是外边梁、中梁、内边梁，单梁、梁格模型建立见图3，其中单梁模型共计55个节点、46个单元，梁格模型共计193个节点、272个单元。

图3 midas Civil分析模型

3 单梁与梁格模型计算结果

单梁、梁格模型的纵向弯矩内力图见图4，可以看出，梁格模型能准确分析3片梁的受力状态。

图4 纵向弯矩内力图

单梁、梁格模型关键位置处内力、挠度计算结果见表1。

表1 单梁、梁格模型内力、挠度计算结果表

由表1可知，梁格模型能较好地考虑大曲率段“弯扭耦合”作用，内力合计值均较单梁模型大，其中单梁扭矩误差达23%，梁格模型更是能体现出由于扭矩导致的外边梁挠度大于内边梁结果。

支反力是曲线梁桥结构设计中的一个重要指标，计算结果见图5。

图5 支反力(单位：kN)

由图5可见，单梁模型中支点内侧支反力大于外侧支反力，但两者差别不大，可视为双支承点平分中支点反力。而梁格模型呈现出外侧支反力大于内侧支反力，与实际更为符合。2个模型在两侧端支点处均为外侧支反力大于内侧支反力，且内外侧支反力差值较大，其中梁格模型更能体现曲线段扭矩导致的外侧支反力增加，相较于单梁模型，其外侧支反力偏大约15%。

上述结论表明梁格模型能较好地反映“弯扭耦合”作用及梁体精细化分析，从设计角度出发，建立大曲率箱梁梁格模型计算分析有助于截面合理配置，并选取适合的支承支座形式。下文将以大曲率箱梁桥对称结构的一半为研究对象，建立梁格模型分析不同参数下边跨和中跨的四分点及二分点截面内力、跨中挠度和支点反力。当考虑某参数影响时，其他参数与本节梁格模型参数保持一致。

4 不同参数影响分析

4.1 不同曲率半径

匝道路线设计受场地限制等因素影响，常采用最小圆曲线半径，导致结构曲率大。本文即选取匝道圆曲线设计中较为常见的4种大曲率半径(R=30，40，60，90 m，对应圆心角分别是30.6°，22.9°，15.3°，10.2°)进行对比分析。

不同曲率半径纵向弯矩对比分析见图6。

图6 不同曲率半径纵向弯矩对比分析图

由图6可见，在最大曲率半径R=30 m时，结构纵向弯矩绝对值明显大于其他曲率半径下的纵向弯矩绝对值。在边支点位置处，纵向弯矩变化最大，当曲率半径从30 m增加至40 m时，中梁边支点纵向弯矩值由282.8 kN·m减小至32.8 kN·m，减小88.4%。曲率半径从40～90 m之间，各梁纵向弯矩值基本相同，可见当曲率半径大于40 m后(圆心角小于22.9°)，曲率半径对纵向弯矩的影响不大。

不同曲率半径扭矩对比分析见图7。

图7 不同曲率半径扭矩和支反力对比分析图

由图7a)～c)可以看出，随着曲率半径的增加，3片梁各点位置的扭矩变化越来越趋于平缓，说明当曲率半径变大时，梁体的“弯扭耦合”作用减小。当曲率半径R=30 m时，中梁最大扭矩和最小扭矩差值为577 kN·m，而当曲率半径R=90 m时，中梁最大扭矩和最小扭矩差值仅为172.9 kN·m，减小70%。曲率半径在40～90 m之间，各梁扭矩值及其变化差值不大，可见当曲率半径大于40 m后(圆心角小于22.9°)，曲率半径对扭矩的影响不大。

不同曲率半径纵向弯矩对比分析见图7d)，可以看出，随着曲率半径的减小，内外侧支反力差值越来越大，其“弯扭耦合”效应对梁体内外侧支反力的影响逐渐增加。

选取内外边梁跨中挠度进行对比分析，结果见图8。

图8 不同曲率半径内外边梁跨中挠度对比分析图

由图8可见，外边梁挠度值大于内边梁，随着曲率半径的增加，外边梁跨中挠度值逐渐减小，内边梁跨中挠度值逐渐增加，内外边梁跨中挠度差值逐渐减小。当曲率半径大于40 m时(圆心角小于22.9°)，曲率半径对挠度的影响较小。

曲率半径变化对梁体的剪力影响较小，限于篇幅，本文不予详细分析。综上所述，当曲率半径小于40 m时，“弯扭耦合”效应明显，不可忽视。

4.2 不同桥宽的影响

通常匝道桥宽度规模以单车道或双车道居多，在小半径大曲率段考虑车道加宽值后，桥梁宽度达9 m(单车道)或10 m(双车道)。本文即选取9 m桥宽与上节10 m桥宽进行对比分析。

不同桥宽纵向弯矩对比分析见图9a)～c)，可以看出，桥宽变化对边跨跨中和中支点的弯矩值影响较大。10 m桥宽相较于9 m桥宽纵向弯矩变化百分值见图9d)，中梁纵向弯矩变化较大，均在10%以上，在支点处增加尤为明显，高达18%；内外边梁变化值较小，且内边梁中跨变化百分值均在5%以内。

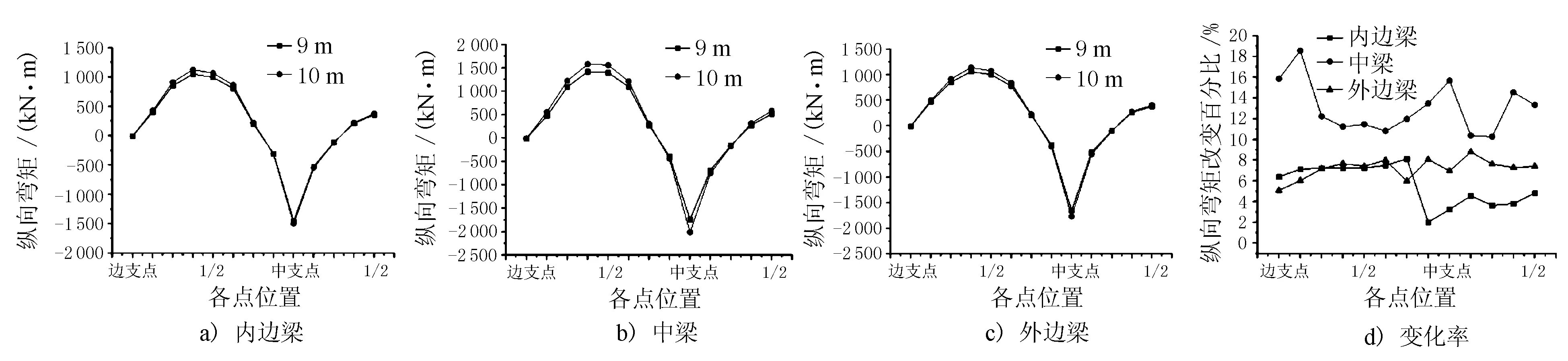
图9 不同桥宽纵向弯矩对比分析图

不同桥宽扭矩对比分析见图10。

图10 不同桥宽转矩对比分析图

由图10a)～c)可见，桥宽变化对支点附近的扭矩值影响较大。扭矩随桥宽变化百分值见图10d)，桥宽变化对内边梁的扭矩影响较大，边中支点处的扭矩值基本增加1倍。

各支承点反力对比见图11。

图11 不同桥宽支反力对比分析图

由图11可见，随着桥宽的增加，同一支点内外支承反力差值增大，且外侧支反力增加值大于内侧支反力，桥宽增加1 m，各支承反力增加约10%。

桥宽变化对中梁剪力值影响较大，这是由于中腹板传递较多剪力造成，限于篇幅，本文不予详述。综上所述，桥宽的变化对支点的纵向弯矩、扭矩及内外侧支反力影响较大，当曲率半径一定时，桥越宽，“弯扭耦合”作用越明显。对于宽桥，应适当增加曲率半径。

4.3 不同跨径的影响

为避免预应力钢筋外崩，当桥梁位于大曲率半径段时，通常选用钢筋混凝土形式，布孔跨径不大于20 m，设计常选用跨径在15～20 m。本文选取16，18，20 m 3种不同跨径进行对比分析。

不同跨径纵向弯矩对比分析结果见图12。由图12可见，跨径的增加对边跨和中支点的纵向弯矩影响较为明显，跨径每增加2 m，边跨纵向弯矩最大值和中支点的负弯矩增加约25%。

图12 不同跨径纵向弯矩对比分析图

不同跨径扭矩对比分析见图13。

图13 不同跨径扭矩对比分析图

由图13可见，跨径的增加对内边梁和中梁的扭矩影响较大，边支点位置处，跨径每增加2 m，内边梁扭矩增加约25%，中梁扭矩增加约34.9%。

不同跨径剪力对比分析见图14。

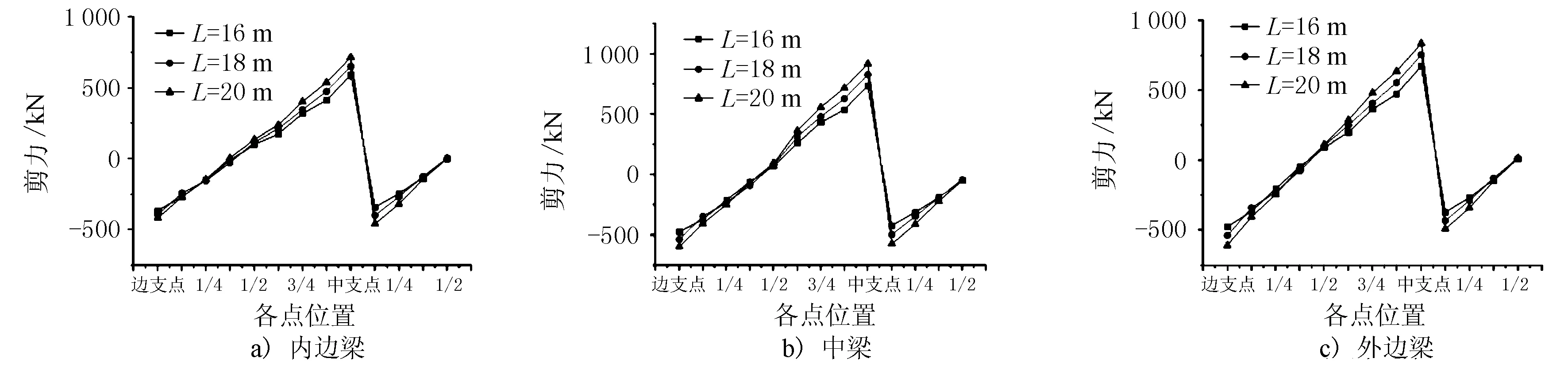
图14 不同跨径剪力对比分析图

由图14可见，跨径的增加对支点附近位置处剪力影响较大，跨径每增加2 m，各梁支点处的剪力值增加约10%。

各支承点反力对比见图15。

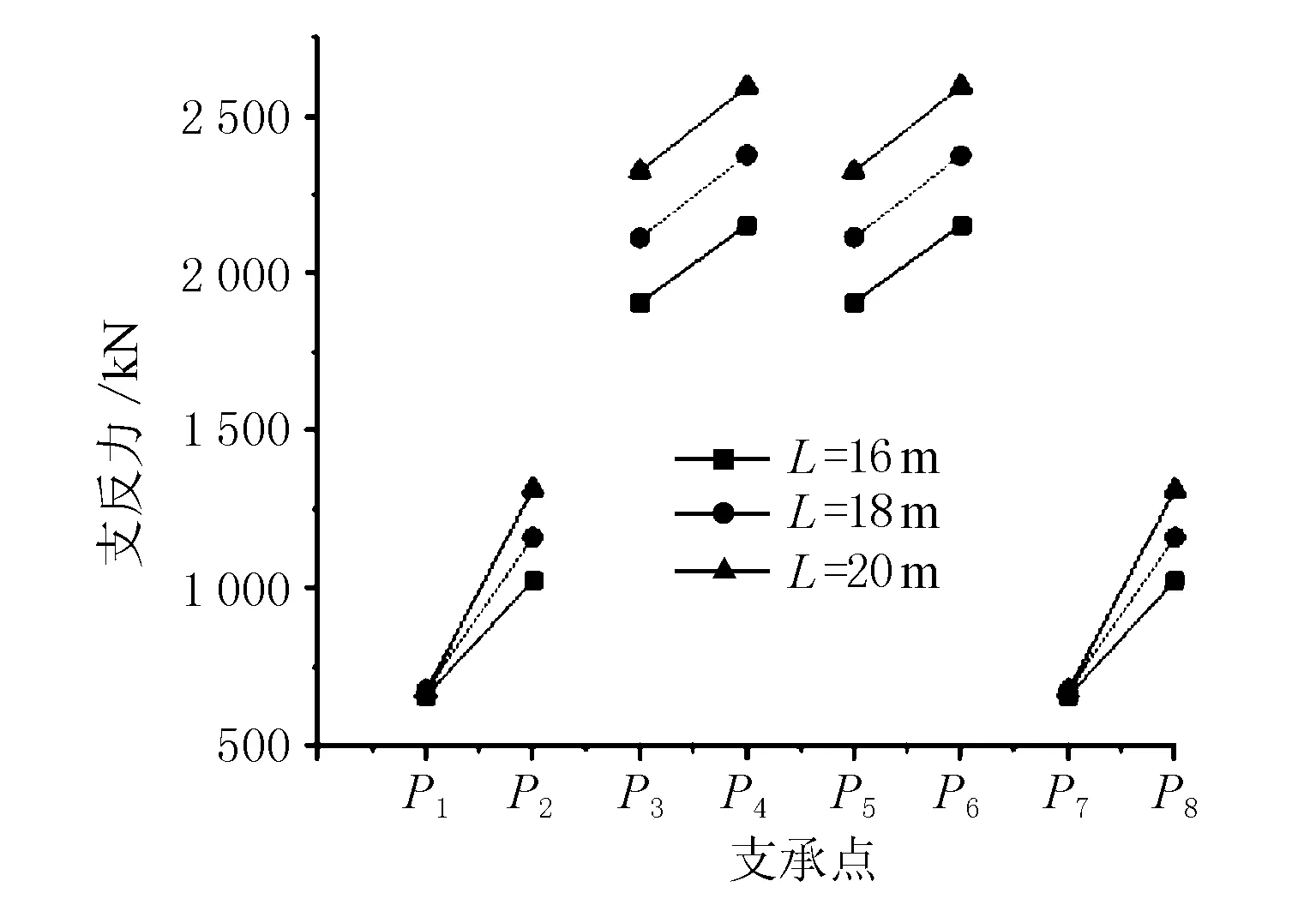
图15 不同跨径支反力对比分析图

由图15可见，跨径的增加对边支点内支承反力(P1、P7)基本无影响，而在其他支承点处支反力则增加约10%，与剪力增加百分值基本符合。边支点内外支承反力差值随着跨径的增加而增加，不利于设计支座选型。

综上所述，随着跨径的增加，“弯扭耦合”作用效应越明显，当跨径一定时，应适当增加曲率半径。

4.4 不同支承形式的影响

对于大曲率半径梁桥来说，不同的支承形式对梁桥的受力有着较大的影响，设计中常见有2种支承布置形式：各支点处双支承、中支点处单支承。本文对这2种支承形式对大曲率箱梁桥受力性能进行分析。

不同支承形式纵向弯矩对比分析见图16。

图16 不同支承形式纵向弯矩对比分析图

由图16可见，中支点单双支承仅对中支点纵向弯矩有影响，且3片梁中支点纵向弯矩总和基本相等，所以，中支点单双支承的形式对箱梁纵向弯矩值影响较小。

不同支承形式扭矩对比分析见图17。

图17 不同支承形式扭矩对比分析图

由图17可见，3片梁单支承时在中支点处均有扭矩突变，其中内边梁中支点扭矩值从1 027 kN·m突变至-528.8 kN·m，变化率151%。故认为支承形式对中梁的扭矩影响较大，中梁边跨各点采用单支承时的扭矩值大于采用双支承时的扭矩值。所以，采用双支承可以减小大曲率箱梁桥的“弯扭耦合”作用，使其受力均衡，变化平缓，有效避免出现过大的扭矩值。

不同支承形式剪力对比分析见图18。

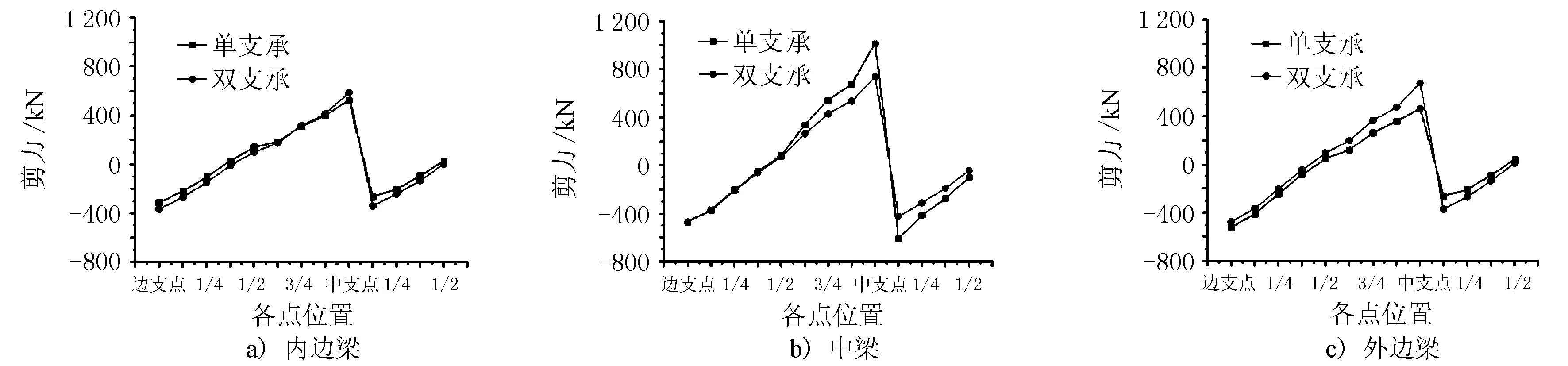
图18 不同支承形式剪力对比分析图

由图18可见，中支点单双支承对中梁和外边梁中支点附近剪力值影响较大。当由双支承变为单支承时，中梁中支点剪力值由735.8 kN增加到1 017.9 kN，增加38%，外边梁中支点剪力值由674.5 kN减小到464.8 kN，减小31%，内边梁中支点剪力值由589.3 kN减小到526.2 kN，减小10.7%。这是由于单支承出现了剪力集中现象。

不同支承情况下支反力值见表2。

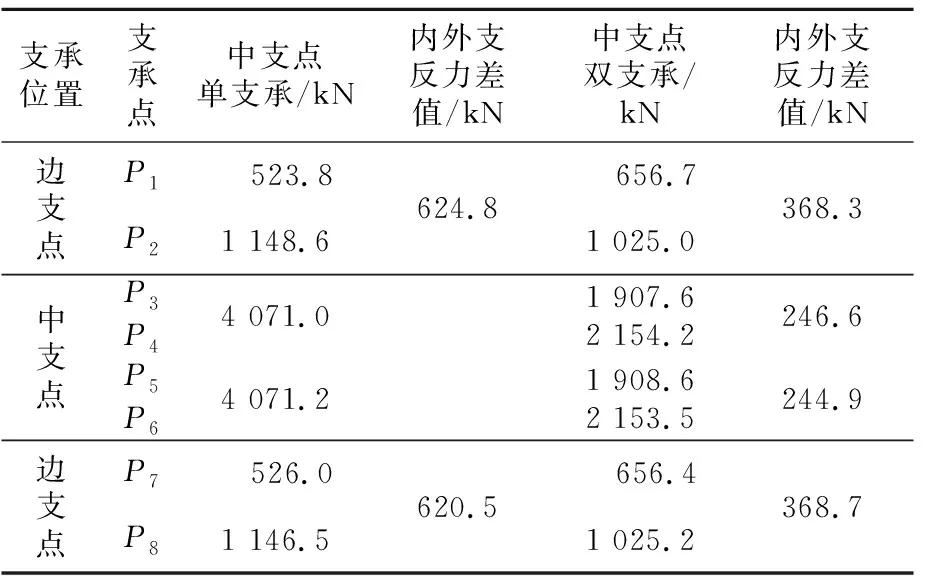
表2 不同支承时支反力情况表

由表2可见，各支承位置处的支反力和基本相等，但中支点单支承形式导致边支点位置处的内外侧支反力差值更大，内侧支反力减小，外侧支反力增加，易进一步造成边支点处内侧支点脱空，造成大曲率半径箱梁桥的抗扭支承消失，横向失稳垮塌。因此，后续大曲率半径箱梁桥的设计应尽量避免采用中支点单支承形式。

5 结论

1) 梁格模型能较好地反应“弯扭耦合”作用及梁体精细化分析，建立大曲率箱梁梁格模型计算分析有助于结构设计。

2) 当曲率半径小于40 m时(圆心角大于22.9°)，结构“弯扭耦合”效应十分明显。

3) 曲线内外侧支反力差值较大，应当注意对支点处抗扭支座的设计，尤其是边支点位置。

4) 中支点采用双支承形式有利于结构受力均衡，有效避免出现过大的扭矩及剪力集中现象。