两类图完美对集数的分类递推计算

唐保祥, 任 韩

(1.天水师范学院 数学与统计学院, 甘肃 天水 741001；2.华东师范大学 数学科学学院, 上海 200062)

1 预备知识

图完美对集的计数理论有广泛的应用,也有重要的理论意义[1-3].目前还没有统一的方法求一般图完美对集的数目.但是,分类嵌套递推理方法是计算许多图类完美对集数的有效方法[4-10].

定义1 若图G有一个1-正则生成子图P,则称这个生成子图P为图G的完美对集.

定义2 设图G是一个有完美对集的图,若图G的两个完美对集P1和P2中有一条边不同,则称P1和P2是G的两个不同的完美对集.

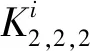
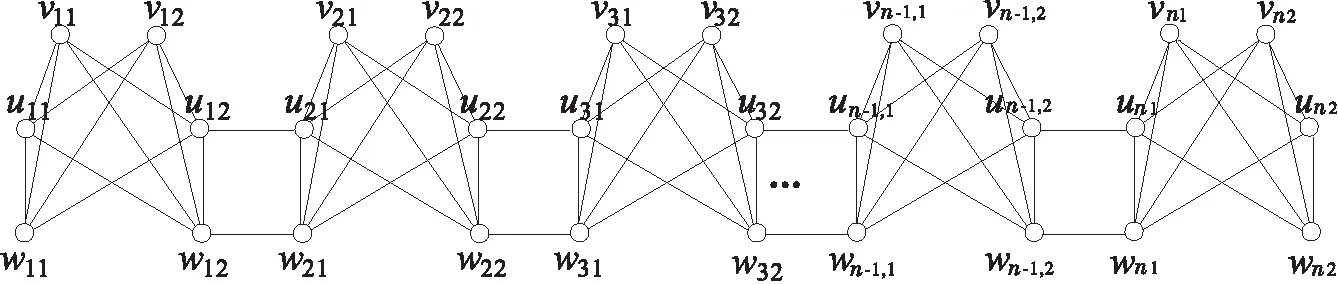
图1 图2-nK2,2,2 Fig.1 Figure of 2-nK2,2,2

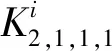
图2 图2-2nK2,1,1,1 Fig.2 Figure of 2-2nK2,1,1,1

2 结果及其证明

定理1 设图2-nK2,2,2的完美对集数为ρ(n),则

证明图2-nK2,2,2存在完美对集是明显的.欲求ρ(n)的解析式,先定义图G1并求出它的完美对集数的递推式.把路ab的端点a,b分别与图2-nK2,2,2顶点u11,w11连接一条边,得到的图记为G1,如图3所示.

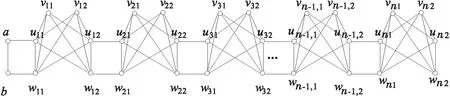
图3 图G1 Fig.3 Figure of G1

图G1显然有完美对集,π(n)表示图G1的完美对集的数.设图G1完美对集的集合为P,图G1包含边ab,au11的完美对集集合分别为P1,P2,则P1∩P2=Ø,P=P1∪P2,故π(n)=|P|=|P1|+|P2|.

因为ab∈P1所以au11,bw11∉P1,由ρ(n)的定义知,|P1|=ρ(n).

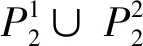
位一直走到窗户旁边，再走回来。我按他的话向前走，心里却十分尴尬。他斜靠在椅背上，手掌托着下巴，神情十分严肃。走完一个来回后，我又重新站到他的面前，然而他一句话也没说。为了掩饰我的窘态，我的眼睛一直没从放在那张空椅下的鞋子上移开。

π(n)=ρ(n)+2ρ(n-1)

(1)

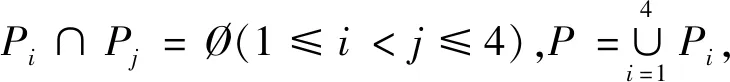
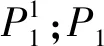
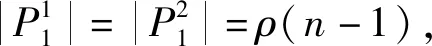
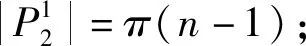
故|P2|=π(n-1)+ρ(n-1).

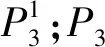
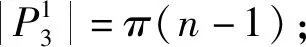
故|P3|=ρ(n-1)+π(n-1).

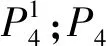
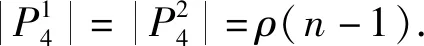
综上所述,

ρ(n)=6ρ(n-1)+2π(n-1)

(2)

把(1)式代入(2)式,得

ρ(n)=8ρ(n-1)+4ρ(n-2)

(3)

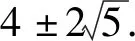
故递推式(6)的通解为

式中c1,c2为待定常数.

由图4知,ρ(1)=8.

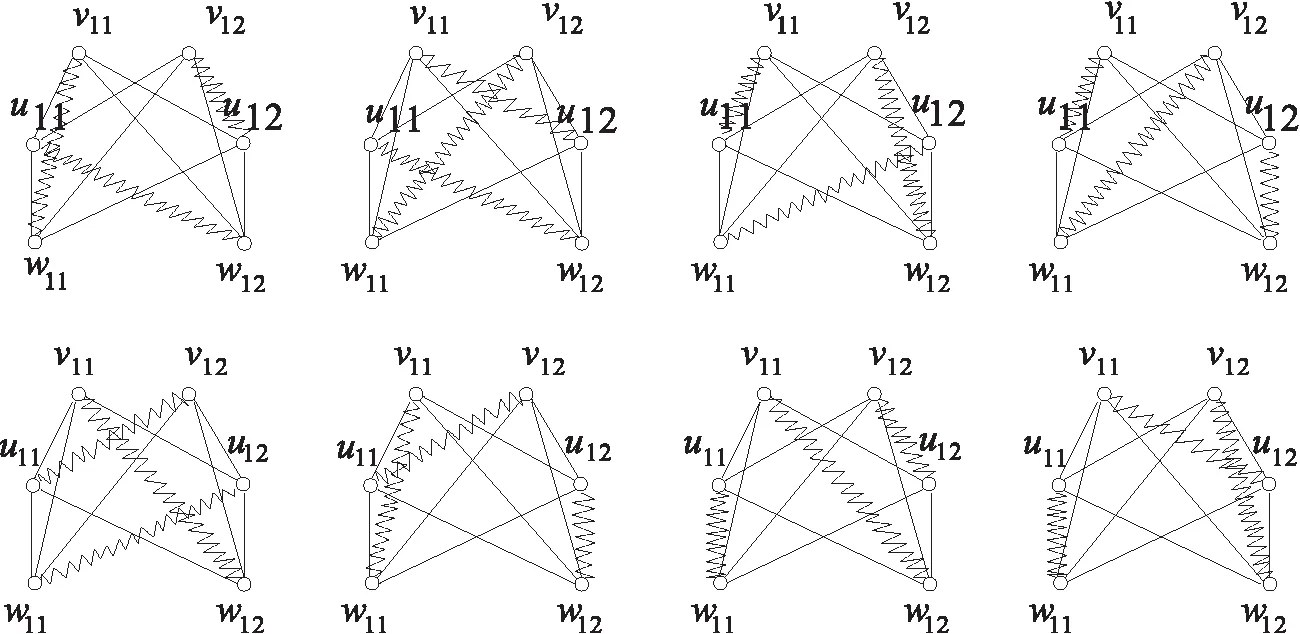
图4 图G2 Fig.4 Figure of G2

由图5知,π(1)=10.

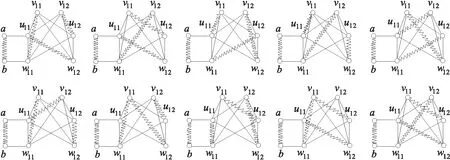
图5 图G3 Fig.5 Figure of G3

所以由(2)得,ρ(2)=68.故

定理2 设图2-2nK2,1,1,1的完美对集数为η(2n),则η(2n)=8n.

证明显然图2-2nK2,1,1,1有完美对集.设图2-2nK2,1,1,1完美对集的集合为P,图2-2nK2,1,1,1含边u13v11,u13v12的完美对集集合分别为P1,P2,则P1∩P2=Ø,P=P1∪P2,故η(2n)=|P|=|P1|+|P2|.

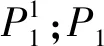
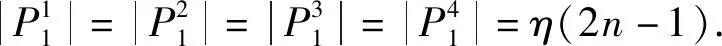
|P1|=4η(2n-1)

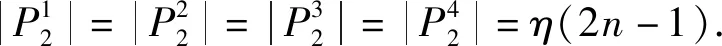
故|P2|=4η(2n-1).

所以η(2n)=8η(2(n-1))=L=8n-1η(2×1).

由图6知，η(2×1)=8.故η(2n)=8n.

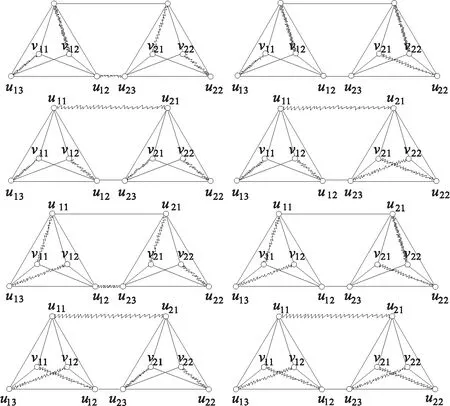
图6 图G4 Fig.6 Figure of G4