基于能量法研究刚性质量块轴向撞击圆柱壳的屈曲
2021-04-28辛朝炜韩志军
辛朝炜, 韩志军
(1. 太原理工大学 机械与运载工程学院,太原 030024; 2. 太原理工大学 生物医学工程学院,太原 030024)
随着现代科学技术迅猛发展,结构屈曲的研究受到广大学者的极大关注。目前静力屈曲问题的研究已较为充分,而动力屈曲问题的研究仍充满挑战。作为结构基本原件的圆柱壳广泛应用于实际生活和各种工程实际中,例如:各种飞行器以及运载火箭主体结构均采用壳体。所以圆柱壳动力屈曲的研究有着很强的工程应用价值、理论价值和重要意义。
Zimicik等[1]忽略应力波效应,用理论和实验研究了满载作用下,径厚比不同的薄壁圆柱壳的轴向动力屈曲,指出圆柱壳的屈曲形式与初缺陷的分布有着密切的关系。Lo Lepik[2]考虑应力波效应,用准分叉法分析了圆柱壳的动力屈曲,用Runge-Kutta法给出其数值解。Bisagni[3-4]忽略应力波效应,使用Abaqus软件对有初缺陷的圆柱壳在轴向冲击载荷下的动力屈曲进行了数值分析,并用实验验证了数值模型,数值计算结果表明初缺陷和载荷持续时间对动力屈曲有影响。Karagiozova等[5-6]考虑应力波效应的影响,给出了圆柱壳发生动力屈曲的条件,用FE码Abaqus/Standard对其进行了数值模拟,表明材料和几何特性对屈曲是有影响的;其实验研究,表明冲击速度对圆柱壳动力屈曲有大的影响,而且材料特性和惯性效应对于屈曲模态的形成有重大影响。Xu等[7-8]通过将哈密顿系统引入圆柱壳的动态屈曲中,考虑应力波效应,得到了哈密顿正则方程的数值解。Fan等[9-10]不考虑应力波效应,导出了圆柱壳在满载作用下屈曲临界荷载随时间变化的解析式,并讨论了圆柱壳径厚比和外压加载速度对屈曲临界载荷的影响。桂夷斐等[11]研究了在轴向阶跃载荷作用下,应力波对圆柱壳动力屈曲的影响,通过数值计算,给出了屈曲临界载荷与临界长度、圆柱壳径厚比的关系。上述研究表明,考虑应力波效应时一般采用阶跃载荷加载,忽略应力波效应时一般以满载方式加载,且研究问题的方法有理论分析、数值模拟或计算机仿真、实验研究,这样考虑问题的角度和所用方法不同,所得结论各异,且对具有工程应用背景的质量块撞击圆柱壳的动力屈曲研究较少也不够深入。Karagiozova等[12-13]考虑应力波效应,利用 Abaqus对在质量块冲击作用下的圆柱壳进行模拟并得到不同的屈曲模态,结果表明,受到高速冲击的壳体,其动力屈曲不仅取决于施加载荷的大小,还取决于初始动能的大小。顾红军等[14]采用落锤实验对圆柱壳的动力屈曲行为进行研究,结果表明圆柱壳的动力屈曲与径厚比有关。马健等[15]对质量块撞击圆柱壳进行实验研究,运用LS-DYNA对其进行了仿真模拟,两者得到的冲击加速度响应曲线基本一致。上述质量块撞击圆柱壳的屈曲表明,因应力波传播比较复杂,这给理论研究带来一定困难,目前主要集中于实验和计算机仿真分析。
基于此,本文考虑应力波效应,利用能量法,建立系统的拉格朗日函数,将经计算获得的符合边界条件的准试函数代入第二类拉格朗日方程,得到二阶线性偏微分方程,分析方程解的特性,得到质量块撞击圆柱壳屈曲临界速度的解析表达式。算例分析,讨论了临界长度、质量比、轴向模态数、环向模态数、径厚比等参数对屈曲临界速度的影响。
1 屈曲临界速度解析表达式的推导
如图1所示,均质钢圆柱壳左端夹支,右端固支,长度为L,半径为R,厚度为h,弹性模量为E,密度为ρ,泊松比μ,横截面积为A,选取柱坐标系x,y,z,其相应的位移为u,v,w。左端受质量为M的刚性质量块撞击。应力波沿x方向传播,如图2所示,当传播到距夹支端为lcr时,圆柱壳受力段发生突然屈曲,且lcr为临界长度,其中lcr=tcr·c。

图1 受刚性质量块撞击的圆柱壳

图2 应力波传播示意图
应力波在圆柱壳内传播[16]
(1)

于是圆柱壳内各段轴力
(2)
当应力波传到lcr时,系统的动能T、应变能U,以及外力功W,可表示为

(3)

Mθκθ+Mxθκxθ}Rdxdθ
(4)
(5)
在小挠度理论下圆柱壳的几何关系为
(6)
(7)
圆柱壳的内力
(8)
内力矩为
(9)

忽略轴向惯性,整理系统动能T、系统应变能U、系统做功W的表达式得到
(10)
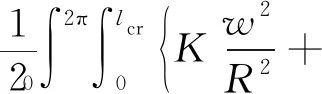
(11)
(12)
设系统的拉格朗日函数为L,有
L=T-U+W
(13)
把式(10)、式(11)、式(12)代入式(13),得到

(14)
可设试函数为
w=f(x,θ)T(t)
(15)
其中,
(16)
式中:n为轴向模态数;m为环向模态数;α和β为相关待定系数。式(15)应满足下述边界条件。

(17)
将式(15)、式(16)代入式(17)中可得
(18)
若式(18)有解,则sinn1π与sinn2π一定同奇偶,即n1=n,n2=n+2。又因为α+β=0,故α=-β,若α=1,则β=-1。得到圆柱壳的有效试函数是
(n=0,1,2,…)
(19)
将试函数式(19)代入式(14),整理得

(20)
根据第二类拉格朗日方程
(21)
把式(20)代入式(21),得
(22)
将方程整理得
(23)
其中,
(24)

(25)
(26)
将式(16)分别代入式(24)、式(25)、式(26)得
C1=-ρhRπlcr
(27)
(28)

(29)
其中,
(30)
分析式(23)解的性质,则有
当C2-C3<0时,得到的解以指数形式随时间扩散,表明圆柱壳已经发生屈曲;
当C2-C3>0时,得到的解是随时间稳态的三角函数,表明圆柱壳不发生屈曲;
当C2-C3=0时,处于屈曲临界状态,这时可得到屈曲的临界条件,其为

(31)
式(31)即为圆柱壳屈曲临界速度解析表达式。
2 算例分析
在算例分析中,取圆柱壳长L=1 m,半径R=0.1 m,厚度h=0.002 m,径厚比k=(2R)/h,E=2×1011Pa,μ=0.3,ρ=7 800 kg/m3。
在m=1,k=200 ,质量比为10,n分别为0,1,2的情况下,临界速度随临界长度的变化关系,如图3所示。

图3 当n不同时,临界速度随临界长度的变化关系图
图3表明:临界速度随临界长度的增大而减小,这也表明应力波效应对动力屈曲有明显影响;曲线可分为敏感区和非敏感区,其分界点约在0.4 m左右,曲线在敏感区变化比较陡,在非敏感区变化比较平缓;当临界长度相同时,临界速度随轴向模态数增大而增大,说明高速冲击越容易激发圆柱壳屈曲的高阶模态。
图4中的曲线可分为敏感区和非敏感区,曲线在敏感区变化比较陡,在非敏感区变化比较平缓;临界速度随临界时间的增加而减小,表明应力波效应对动力屈曲有明显影响。与Karagiozova等研究所得曲线变化规律、结论一致。

图4 临界速度与临界时间的变化关系曲线
在n=0,k=200 ,质量比为10,m分别为1,2,3的情况下,临界速度随临界长度的变化关系,如图5所示。

图5 当m不同时,临界速度随临界长度的变化关系图
图5表明:临界速度随临界长度的增大而减小,这也表明应力波效应对动力屈曲有明显影响;曲线敏感区和非敏感区的分界点约在0.3 m左右,结合图3,表明:轴向模态对屈曲的影响比环向模态还要明显;当临界长度相同时,临界速度随环向模态数增大而增大,说明高速冲击容易激发圆柱壳屈曲的环向高阶模态;临界长度约在0.1左右时,曲线几乎重合,说明高速下屈曲模态跃迁不明显,这与轴向模态对屈曲的影响有不同之处。
在m=1,k=200 ,lcr=0.4 m,n分别为0,1,2的情况下,临界速度随质量比的变化关系,如图6所示。

图6 当n不同时,临界速度随质量比的变化关系图
图6表明:临界速度随质量比的增加而减小,表明初始动能对屈曲有明显影响,这与Karagiozova等研究中数值模拟所得曲线变化规律、结论一致;曲线可分为敏感区和非敏感区,其分界点约在质量比为5左右;在质量比相同时,临界速度随轴向模态数增大而增大,初始冲击动能也随模态数增大而增大,进一步说明初始动能对屈曲有明显影响,同时也说明高速冲击或较大的初始动能容易激发圆柱壳屈曲的高阶轴向模态。
在n=0,k=200 ,lcr=0.4 m,m分别为1,2,3的情况下,临界速度随质量比的变化关系,如图7所示。

图7 当m不同时,临界速度随质量比的变化关系图
图7表明:临界速度随质量比的增大而减小;曲线可分为敏感区和非敏感区,其分界点约在质量比为5左右;在质量比相同时,临界速度随环向模态增大而增大,初始冲击动能也随模态数增大而增大,说明初始动能对屈曲有明显影响,同时也说明高速冲击或较大的初始动能容易激发圆柱壳屈曲的高阶环向模态。
在n=0,m=1,质量比为10,改变k,使其分别为100,150,200的情况下,临界速度随临界长度的变化关系,如图8所示。
图8表明:临界速度随临界长度的增大而减小,这也表明应力波效应对动力屈曲有明显影响;曲线敏感区和非敏感区的分界点约在lcr=0.4 m左右;在临界长度相同时,临界速度的变化随径厚比的减小而增大,这说明径厚比越大,高速冲击越容易激发圆柱壳的屈曲。
在n=0,m=1,lcr=0.4 m,改变k,使其分别为100,150,200的情况下,临界速度随质量比的变化关系,如图9所示。

图9 当k不同时,临界速度随质量比的变化关系图
图9表明:临界速度随质量比的增大而减小;曲线敏感区和非敏感区的分界点约在质量比为7左右;在质量比相同时,临界速度随径厚比的减小而增大,初始冲击动能也随径厚比的减小而增大,这说明径厚比越大,高速冲击越容易激发圆柱壳的屈曲。这与顾红军等所得的规律、结论一致。
3 结 论
本文通过理论研究和算例分析得出以下结论:
(1)基于能量法,考虑应力波效应,建立了拉格朗日函数,将获得的满足边界条件的准试函数代入第二类拉格朗日方程,得到圆柱壳屈曲临界速度的解析表达式。
(2)算例分析,讨论了轴向模态数、环向模态数、径厚比、临界长度、质量比对动力屈曲的影响,结果表明:
当模态数不同时,临界速度和临界长度的关系曲线可分为较陡的敏感区和变化平缓非敏感区,临界速度随临界长度的增加而减小,表明应力波效应对圆柱壳的动力屈曲有明显影响;临界速度与质量比的关系曲线也可分为敏感区和非敏感区,当质量比相同时,初始冲击动能随模态数增大而增大,表明初始动能对屈曲有明显影响;临界速度随模态数增大而增大,说明高速冲击容易激发圆柱壳屈曲的高阶模态。
当径厚比不同时,临界速度随径厚比的减小而增大,这说明径厚比越大,高速冲击越容易激发圆柱壳的屈曲。
