滚动碰撞式调制质量阻尼器力学模型及参数分析

2021-04-28黄绪宏闫维明许维炳王宝顺

振动与冲击 2021年8期

黄绪宏，闫维明，许维炳，王宝顺

(北京工业大学工程抗震与结构诊治北京市重点试验室，北京 100124)

颗粒阻尼器作为一种被动控制减振装置，通过振动过程中颗粒与主结构之间的动量交换及碰撞耗能实现对系统的控制。颗粒阻尼器的构造简单、成本低廉、易于实现，一直是机械领域及航空航天领域的研究热点，其中具有代表性的是单颗粒冲击阻尼器。Masri等[1-2]对单颗粒冲击阻尼器进行了详细的理论研究，获得了单自由度结构及多自由度结构稳态解析解。Li等[3-4]分别以单自由度结构及多自由度结构作为试验对象，研究不同缓冲材料对颗粒阻尼减振效果的影响，结果表明缓冲型阻尼器不仅减小了结构加速度及冲击力，而且相比传统冲击型阻尼器具有更好的减振效果。单颗粒阻尼器力学模型较为清晰，其在一定程度上也推动了多颗粒阻尼器的相关研究。Papalou等[5]及鲁正等[6]将多颗粒等效为单颗粒，在单颗粒研究的基础上对多颗粒进行相应理论分析，系统分析了多颗粒阻尼器减振机理及参数影响规律。

单颗粒冲击阻尼器虽然理论模型较简单，但在实际应用中，初始时刻冲击质量块处于随遇平衡状态，这对该型阻尼器的减振效果及理论分析结果的合理性有影响，且传统单颗粒冲击阻尼器冲击力较大。相比之下，具有一定弧度的滚动碰撞式调制质量阻尼器 (pounding tuned rotary mass damper, PTRMD) 的提出解决了初始平衡状态的缺陷，能够在一定程度上减小碰撞时刻的冲击力。陈俊岭等[7]基于调谐质量阻尼器及颗粒阻尼器的工作原理提出一种适用于风力发电塔架振动控制的盆式调谐/颗粒阻尼器，并将其应用于1.5 MW陆上风机振动控制中，实测分析结果表明该型阻尼器能有效地控制塔架在急停工况及运行工况下的振动。王见祥[8]在滚动型调谐质量阻尼器研究基础上提出了PTRMD，并采用数值仿真的方式验证了其对单自由度结构及多自由度结构[9]在简谐激励及地震作用下的减振效果。现阶段研究成果表明，PTRMD能有效地减小受控结构的动力响应，但仍然存在以下几方面不足：①PTRMD力学模型仍不完善，颗粒振动过程中可能存在黏滞振动现象；②PTRMD是在调谐质量阻尼器的基础上提出的，其曲率半径是按照最优调频进行计算取值，但这种取值方法的合理性还有待验证；③PTRMD主要物理参数对其减振控制效果的影响规律并不明确，仍处于探索阶段。

鉴于此，本文以PTRMD作为研究对象，基于经典力学法中的碰撞恢复系数并考虑颗粒黏滞振动，建立PTRMD力学模型及PTRMD-单自由度结构运动微分方程，最后通过数值模拟的方法研究容器曲率、碰撞恢复系数等参数对PTRMD减振效果的影响规律，为PTRMD的应用及多颗粒滚动碰撞式调制质量阻尼器的进一步研究做铺垫。

1 PTRMD运动分析模型建立及其求解

基于 PTRMD 的单自由度受控结构力学模型,如图1所示，假设颗粒初始位置位于容器底部，两侧碰撞间距均为θmax，则颗粒在容器中运动状态主要包括以下三个阶段：未碰撞阶段、碰撞阶段、黏滞振动阶段[10]，各阶段运动方程建立如下。

图1 PTRMD力学模型

1.1 未碰撞阶段颗粒运动方程建立

本文基于Lagrange方程推导受控结构体系运动微分方程，认为颗粒在运动过程中只产生滚动摩擦，则受控结构体系动能、势能及非保守力做功为

(1)

(2)

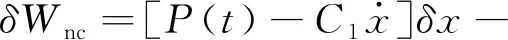
(3)

式中：T为系统动能；V为保守力对应势能；δWnc为非保守力做功；m1，m2分别为结构质量及颗粒质量；R，r分别为容器曲率半径和颗粒半径；K1，C1为结构刚度及阻尼；J=2/5m2r2为颗粒转动惯量；μf为滚动摩擦因数；g为重力加速度；x(t)为结构相对地面的位移；θ(t)为任意时刻颗粒相对结构转动角度；δx,δθ分别为结构位移及颗粒位移对应的虚位移；xa,ya为任意时刻颗粒相对容器底部水平位移及竖向位移；P(t)为外部荷载作用。假设颗粒在运动过程中滚动角度θ为小量(0～0.3 rad)[11]，可将体系动能、势能及非保守力做功分别近似为

(4)

(5)

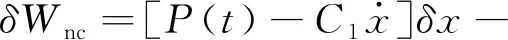
(6)

由Lagrange方程推导结构体系运动微分方程组为

(7)

1.2 基于经典力学法的碰撞恢复模型建立

(8)

式中:i=1,2分别为结构和颗粒；s=n,t分别为碰撞接触面的法向和切向。基于碰撞恢复系数e的定义有

(9)

由式(5)、式(6)得碰撞后速度为

(10)

(11)

1.3 黏滞振动简化方法

(12)

(13)

图2 颗粒黏滞振动

图3 颗粒黏滞运动极限状态

2 颗粒阻尼器自身参数对减振效果影响分析

以某单层钢框架模型[13]作为研究对象建立附加PTRMD体系运动微分方程，利用四阶Runge-Kutta法求解减振体系运动状态，并进行参数分析。模型m1=17.96 kg，K1=5.4 kN/m，结构阻尼比为2%，其振动基频ω0为17.34 rad/s。为研究PTRMD在简谐激励(P(t)=Am1sin(ωt))作用下各物理参数对减振效果的影响规律，选取基本参数如表1所示。文中除特殊说明外，参数按照表中数据取值。采用减振率β对碰撞阻尼器减振效果进行评价，减振率计算公式为

(14)

式中：X+为受控结构响应；X为原结构响应。

表1 基本参数选取

1.1 容器曲率半径R及碰撞距离θmax对减振效果的影响分析

容器曲率半径R及碰撞间距θmax为影响PTRMD减振效果的主要因素。学者们对于曲率半径的选取目前普遍通过调整曲率半径的大小将颗粒滚动频率调至主结构1阶频率附近[14]，其中颗粒滚动频率由式(7)得

(15)

式中，ρ=R-r。

即便如此，不同学者选取颗粒的碰撞间距也存在差异。为研究容器曲率半径及碰撞间距对减振效果的影响，除选取结构基频对应的曲率半径0.053 4 m外，另外选取曲率半径R为[0.04 m,10 m]，对应选取最大碰撞间距θmax在[0，0.3 rad]进行参数分析，并对参数进行无量纲化处理得到颗粒运动的频率比λ及碰撞间隙比γ为

(16)

(17)

式中：ωn为颗粒振动频率，如式(12)所示；ω0=17.34 rad/s为结构基频；Am1Rd为共振时结构稳态位移响应，其中激励幅值A默认为0.5g，Rd为共振放大系数。部分曲率半径及碰撞间距组合对应分析结果如图4～图6所示。为更加清晰的描述减振规律，图中虚线部分为对应组合下考虑颗粒大位移时对应的阻尼器减振率。参数分析结果显示：

(1)由图4可知，当频率比λ较小(λ≤0.17)时，结构稳态位移响应减振率随碰撞间隙比γ的增大总体呈现增长趋势，但在碰撞间隙比增大过程中存在几处明显的极大值点(A,B,C)，依次对应颗粒不同的稳定状态(见图5)；当λ较大时(λ>0.17)，稳态位移响应随γ先增大后减小，最优碰撞间隙比γ及减振率随λ的增大而减小。值得注意的是，当γ=0时对应原结构附加同等质量块下的减振率。

图4 结构稳态位移响应减振率

图5 颗粒碰撞状态

(2)由图6可知，结构最大响应减振率随γ先增大后减小。频率比λ较小(λ≤0.17)时，当γ<0.4，减振率受λ影响较小，当γ>0.4时，减振率随λ的增大而增大；λ较大(λ>0.17)时，最优碰撞间隙比γ及减振率随λ的增大而减小。

图6 结构最大位移响应减振率

(3)为研究颗粒碰撞状态对稳态结构响应的影响，本文采集了结构稳态周期运动状态下颗粒的周期碰撞次数，如图7所示。分析结果表明，当无量纲碰撞间距γ较小时(γ<0.01)，颗粒发生黏滞振动，随着γ的增加黏滞持续时间减小，实际统计到的颗粒碰撞次数增加；当γ>0.01时，颗粒周期碰撞次数随无量纲碰撞间距γ的增加呈指数衰减，且变化规律受λ影响较小。图7与图4对比结果显示，当频率比λ较小时(λ≤0.17)时，颗粒周期碰撞次数越小，对应结构稳态响应减振率越大，当颗粒发生周期2次碰撞时(状态C)，共振时减振效果最好，该结论与文献[15]分析结果一致。当频率比λ>0.37时，由于容器曲率对颗粒运动状态影响显著，单颗粒阻尼器减振机理发生改变。随着λ的增加，最优减振率对应碰撞次数增加。

图7 颗粒碰撞次数统计

2.2 滚动摩擦因数μf对减振效果的影响分析

对于低速运动的土木工程结构来说，颗粒与容器之间的滚动摩擦因数μf对于颗粒阻尼器减振效果的影响是一个不容忽略的影响因素[16]。参数选取如表2所示。

表2 滚动摩擦因数μf影响分析对应参数选取

滚动摩擦因数对颗粒阻尼器减振效果影响，如图8所示。当λ=0.05，γ=0.43时，此时颗粒运动并非稳态最优减振状态，减振率随着摩擦因数的增加先增加后减小，当滚动摩擦因数取0.03 m时达到最优减振效果，此时颗粒运动对应更为稳定的状态，如图9所示。当λ=0.17，γ=0.57时，此时颗粒运动为稳态最优减振状态，当滚动摩擦因数取值较小时，滚动摩擦因数对于稳态状态下颗粒阻尼器减振效果影响较小，但当滚动摩擦因数较大时(uf>0.02)，滚动摩擦因数消耗了较多的颗粒动能，促使颗粒无法与碰撞板发生碰撞，产生了减振效果的突变。当λ=1，γ=0.014时，在当前滚动摩擦因数数量级下，由于摩擦因数较大，已经严重限制了颗粒的运动，造成算法无法正常进行，但部分结果显示，较大的滚动摩擦力对于减振效果是不利的。

图8 滚动摩擦因数对稳态位移响应减振率影响

图9 颗粒运动状态(λ=0.05，γ=0.43)

2.3 碰撞恢复系数e对减振效果的影响分析

碰撞恢复系数e能够反映碰撞过程中颗粒的耗能作用，试验研究表明适当的降低碰撞恢复系数有利于降低结构的位移响应及冲击力[17]，本文在频率比λ=ωn/ω0及碰撞间隙比γ对减振效果影响分析基础上，选取不同的碰撞恢复系数进行共振条件下参数分析，参数选取如表3所示。

表3 碰撞恢复系数e影响分析对应参数选取

分析结果显示，当碰撞间隙比γ较小时，此时颗粒在容器中通过碰撞进行动量交换并不充分，颗粒碰撞主要起到耗能作用，因此当碰撞恢复系数e取值较小时，减振效果较优，如图10所示；随着碰撞间距的增加，颗粒与容器之间的动量交换变为主要影响因素，过低的碰撞恢复系数e反而不利于颗粒的连续稳定的冲击减振，因此碰撞间隙比γ越大对应的最优弹性恢复系数e越大，如图11所示。其次分析结果显示，频率比λ对于最优碰撞恢复系数e的取值也有影响。

图10 碰撞恢复系数e对结构位移响应的影响(λ=1)

图11 碰撞恢复系数e对结构位移响应的影响(λ=0.17)

2.4 颗粒附加质量比对减振效果的影响分析

需要说明的是实际条件下质量比的增加势必会引起频率比λ及碰撞间隙比γ的改变，进而影响颗粒在腔体中的运动状态，而多种因素的耦合会提高质量比影响规律的分析难度。因此，本文在考虑质量比影响时仅通过调整颗粒的密度来获得不同的质量比，对应选取表3中参数进行附加质量比影响分析，其中稳态较优状态对应减振变化规律，如图12所示。

图12 附加质量比μ对减振效果影响分析

由图12可知，当λ=0.05，γ=0.61时，最优附加质量比为7%，此时对应减振率为0.92；当λ=0.17，γ=0.57时，最优附加质量比为8%，此时对应减振率为0.93；当λ=1.00，γ=0.008时，在本文计算条件下，PTRMD的减振控制效果随质量比增加而增加，但其减振控制效果与附加质量基本一致，对应的减振率小于0.7。PTRMD的减振控制效果随质量比变化过程如下。①当λ=0.05，颗粒的附加质量比较小时(μ≤7%)，颗粒的无碰撞限制最大位移仍较大，颗粒与容器之间仍能发生有效的碰撞，颗粒与容器之间的能量交换及碰撞耗能随附加质量的增加而增加，PTRMD的减振效果增加；当7%<μ<10%时，颗粒的无碰撞限制最大位移进一步减小，颗粒与容器之间碰撞的稳定性降低，颗粒与容器之间的能量交换及碰撞耗能均降低，PTRMD减振效果降低，且此过程PTRMD减振效果的稳定性降低；当μ≥10%时，颗粒的无碰撞限制最大位移进一步减小，颗粒与容器不再发生碰撞，此时颗粒仅起到调谐作为，随着附加质量比的增加，PTRMD减振效果增加(与无阻尼调谐质量阻尼器类似);②当λ=0.17，μ≤8%时，与λ=0.05的减振分析过程类似，此时颗粒的无碰撞限制最大位移仍较大，颗粒与容器之间仍能发生有效的碰撞，颗粒与容器之间的能量交换及碰撞耗能随着附加质量的增加而增加，PTRMD的减振效果增加；而当μ>8%时，颗粒与容器之间碰撞的稳定性降低，颗粒与容器之间的能量交换及碰撞耗能均降低，PTRMD减振效果降低，且此过程PTRMD减振效果的稳定性降低，但相比较于λ=0.05，由于无碰撞限制时颗粒运动幅值增加，颗粒将会在较大附加质量比情况下仍然与结构发生碰撞，提高了单颗粒PTRMD受附加质量比影响的鲁棒性;③当频率比λ较大时(λ=1)，由于颗粒运动碰撞间隙比γ较小，颗粒与容器之间的相对位移及相对速度较小，颗粒与容器之间虽能够发生碰撞，但颗粒与容器之间的动量交换及耗能均十分有限，因此PTRMD的减振效果较差，几乎与附加质量相同。

3 外部激励对减振效果影响分析

3.1 激励幅值对减振效果的影响分析

选取激励幅值为0.5g作用下最大位移最优状态下参数(见表3)进行共振条件下激励幅值对减振效果的影响分析，数值分析结果如图13所示。结果显示:①频率比λ较小(λ≤0.17)时，当简谐激励幅值小于0.5g时，随着激励幅值的减小，颗粒在非碰撞状态下最大位移减小，相比之下碰撞间距越来越趋近于对应激励幅值最优碰撞间距，所以随着加速的减小，减振率增加，但是，当激励幅值过小时，由于对应激励幅值下颗粒运动幅值过小，无法与碰撞板发生碰撞，反而发生了减振效果的突变；当简谐激励幅值大于0.5g时，随着幅值的增大，碰撞间隙比减小，减振率降低;②频率比λ较大(λ>0.17)，当激励幅值大于0.1g时，此时由于碰撞间隙比γ较小，颗粒减振效果并不理想；随着激励幅值的减小(<0.1g)，由于结构位移减小，对应激励幅值下的碰撞间隙比γ增大，颗粒与容器之间的动量交换更加充分，因此提高了阻尼器的减振率。值得注意的是，当激励幅值极小时，颗粒不发生碰撞，此时共振状态下减振效果接近完全消振。

图13 激励幅值A对减振效果影响分析

考虑到实际工程结构中，结构可能经历的最大加速度峰值覆盖范围较广，激励幅值对于减振影响规律可能存在差异性，本文选取曲率半径R在[0.04 m,10 m]，对应选取最大碰撞间距θmax在[0,0.3 rad]，选取激励幅值在[0.1g,0.6g]进行参数分析，分析结果如图14、图15所示。分析结果显示，当频率比λ较小时(λ≤0.17)，如图14所示。减振率随γ的增加而线性增加，当碰撞间距临近颗粒极限碰撞间距时，减振率发生突变。激励幅值对减振率变化规律影响较小，但须注意碰撞间距比γ相同时，不同激励幅值对应的实际碰撞间距θmax不同；当λ较大时(λ>0.17)时(见图15)，减振率随γ变化规律并非一致，随着激励幅值的增加，减振率衰减更加迅速。碰撞间隙比对减振效果影响分析与现有研究成果对比显示，当频率比λ≤0.17时，减振率随碰撞间距比变化规律与文献[18]数值仿真结果较为一致，但须注意的是，在多颗粒情况下，本文所得变化规律与文献[18]实测减振率变化规律存在差异，因此多颗粒阻尼器等效单颗粒方法适应性还需进一步研究。

图14 碰撞间隙比γ及激励幅值A对减振效果的影响分析(λ=0.17)

图15 碰撞间隙比γ及激励幅值A对减振效果的影响分析(λ=1)

3.2 激励频率对减振效果的影响分析

为研究激励频率对减振效果的影响，选取表3中稳态较优状态进行参数分析，数值仿真结果如图16所示，由图像分析可知，当频率比λ较大时(λ>0.17)，在当前碰撞间隙下，颗粒以碰撞耗能为主，减振效果并不理想。当λ较小时(λ≤0.17)，由于碰撞间隙比接近颗粒的最大碰撞间隙比，因此只有在频率比ω/ω0接近1时颗粒才能与碰撞板发生碰撞，从而起到减振的效果。λ=0.17与λ=0.05对比显示，适当减小容器曲率半径有利于提高阻尼器的频带作用宽度。

图16 激励频率比ω/ω0对减振效果影响分析(A=0.5g)

在上述分析过程中，由于激励幅值选取较大，当λ较大时，对应碰撞间隙比γ较小，颗粒减振效果并不理想。为研究λ=1时对应阻尼器减振效果，进行了激励幅值A=0.1g,A=0.05g,A=0.01g时频率比ω/ω0对减振效果影响分析，分析结果如图17所示。从图17可知，随着激励幅值的减小，对应碰撞间隙比γ增大，颗粒阻尼器减振效果有所改善。