OFDM水声通信CS限幅失真补偿与LS信道估计优化算法∗

郭铁梁 李志军 张文祥

(梧州学院电子与信息工程学院 梧州 543002)

0 引言

正交频分复用(Orthogonal frequency division multiplexing, OFDM)技术能够有效抑制水声信道较为严重的多径效应，所以这种技术被广泛地应用于水声通信系统中。由于OFDM 信号会出现信号瞬时功率峰值远大于平均功率值的高峰均比(Peak to average power ratio, PAPR)现象，这种高PAPR不但会使系统的性能下降，而且会降低功率放大器(High-power amplifier, HPA)等硬件设备的工作效率，尤其对于多数采用电池供电的水下通信移动设备来说，过高的PAPR 会产生较大的能量供应问题[1]。另外，最小二乘(Least square, LS)信道估计方法因其较小的运算量得到关注，但由于这种算法受噪声影响较大，所以制约了这种方法的广泛应用，特别对于高噪声的水下通信环境，LS 算法的使用受到了更大的限制。目前，研究PAPR 的方法通常包括编码类、概率类和预畸变类等，其中人们研究及使用较多的是预畸变类方法中的限幅法。实践表明，限幅法对PAPR 具有高效的抑制作用，但由于这种方法是一种非线性操作，所以会引起信号的畸变。通常情况下，限幅法导致的非线性失真可通过相应的补偿算法得到解决，例如可以通过发送端编码，或通过迭代判决辅助重构法恢复原始数据，但这些方法大多需要传送辅助数据，以牺牲通信系统有效性为代价[2]。针对传统限幅方法中存在的上述问题，如将限幅畸变看作一个不同于加性高斯白噪声的新噪声，它实际是一种具有稀疏特性的负脉冲[3]，可称其为稀疏限幅噪声，结合限幅脉冲噪声数据的这种稀疏特性和LS 算法特性，本文提出了一种基于压缩感知(Compression sensing, CS)技术的补偿PAPR 非线性失真与LS 降噪算法相结合的优化算法，这种方法主要利用导频数据，通过CS 技术中相应算法在接收端进行限幅补偿，同时对LS信道估计进行降噪优化计算。

1 系统模型

1.1 CS算法模型

CS 理论的核心问题是求解加权系数N ×1 维列向量θ的过程，接收机可采用适当的搜索算法在θ的解空间获得最优解。主要的优化搜索算法有两类，第一类是基追踪(Basis pursuit, BP)算法，第二类是正交匹配追踪(Orthogonal matching pursuit,OMP)算法。考虑重构误差，BP算法可表示[4−6]为

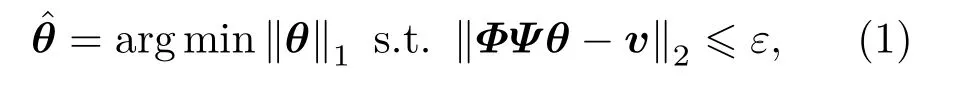
式(1)中，ε表示一个很小的误差容忍值。

由于BP 算法运算量很大，影响信道估计的实时性(特别对于时变水声信道)，所以在实际水下环境中很难得到应用。而OMP 算法利用递归方式减少迭代次数，再通过使用多于BP 算法需要的采样数目，大幅降低了运算量，所以更适用时变水声信道[7]。由于本文只是做仿真实验，所以后面的仿真过程还是利用BP算法得到的。

1.2 OFDM的稀疏限幅噪声

由于有些OFDM 时域离散信号x(n)的幅值可能超过HPA 的工作范围，因此在x(n)被送入HPA之前须进行限幅处理，经限幅之后的数据c(n)与原数据x(n)之间的差值可表示为

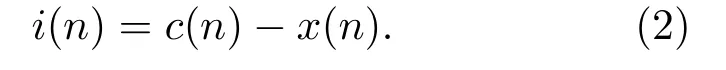
对于整个水声通信系统来说，式(2)中数据i(n)可以看作一种负的脉冲噪声，由于x(n)中较大幅值数据出现的概率较小，因此这种脉冲噪声数据在时域上具有稀疏特性。基于i(n)的这一特点，可以利用CS 技术在系统接收端通过相应的算法对i(n)加以恢复，从而对限幅引起的非线性失真加以补偿，限幅后的数据在接收端的基带离散信号可表示为

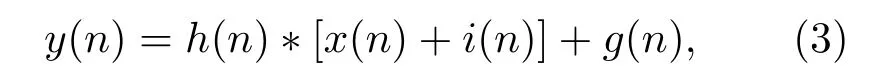
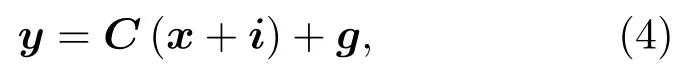
其中，C由h(n)决定，为N ×N维信道循环矩阵，其作用是将多径水声信道的脉冲响应与时域信号做卷积运算[8]，y、x、i、g分别表示N ×1 维列矩阵向量。将式(4)两边同时进行离散傅里叶变换(Discrete Fourier transform, DFT)，进而可得到式(4)的频域表达：

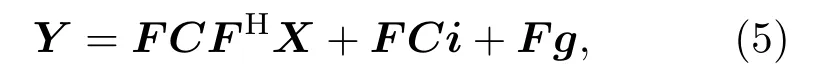
其中，F表示DFT矩阵，FH表示离散傅里叶逆变换(Inverse discrete Fourier transform,IDFT)矩阵，由式(5)在接收端利用式(6)可得到X的估计值[9]：

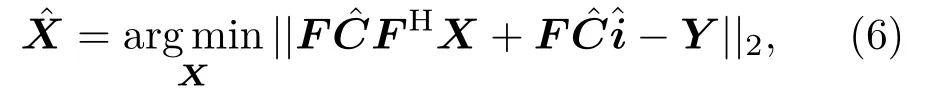
2 基于CS理论及导频数据的限幅噪声补偿算法

2.1 基于导频子载波的限幅噪声估计

由于在OFDM 系统中有Np个导频子载波，而导频子载波处的数据在接收端是已知的，所以接收端收到的实际导频数据与已知导频数据的差值就是导频处的噪声数据，而这个噪声中包含具有稀疏特性的限幅噪声和限幅信号经过多径水声信道之后高斯白噪声。

设OFDM 系统中Np个导频子载波的子载波序号集合用P ={p1,p2,···,pNp}表示，根据式(5)，接收端导频子载波上频域数据可表示为

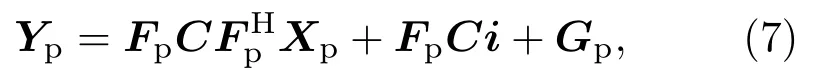
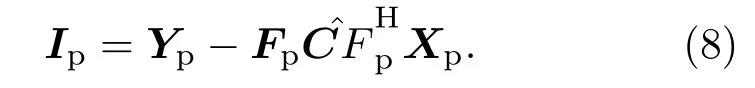
又由式(7)，所以式(8)变为

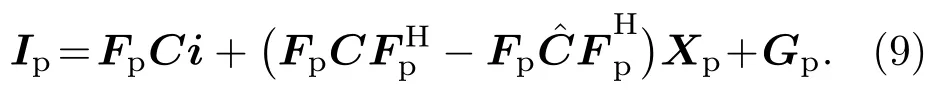
根据CS理论，定义测量矩阵：

再令ic=Ci，则式(9)变为

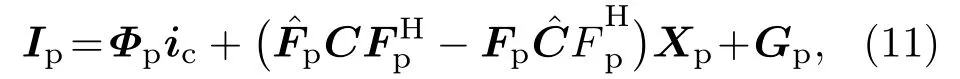
其中，向量ic表示限幅脉冲稀疏噪声通过水声信道之后的时域值，式(11)方程右边第2 项表示导频处信道估计产生的误差。

结合式(1)和式(11)，可得

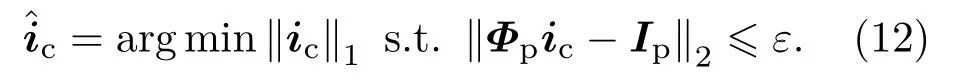
利用式(12)，在设定一个误差容忍值ε和已知信道响应估计初值的前提下就可得到，从而再利用式(6)对限幅所产生的非线性失真进行补偿得到，而误差容忍值ε的设定由2.2节完成。

2.2 基于LS算法的误差容忍值ε的设定

首先通过LS 信道估计得到的Np个导频信道估值,Np−1，再将这些数据进行Np点IDFT，得到Np点时域序列：

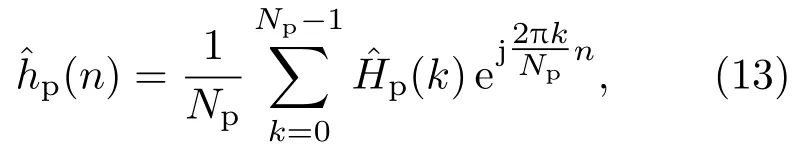
其中，n= 0,1,2,···,Np−1。然后对式(13)做降噪处理，将Np个响应值保留L个有效路径，其余置“0”，如果信道的时延信息未知，可保留循环前缀或者通过设置噪声门限的方法确定L的值。降噪处理后得到Np点时域序列：

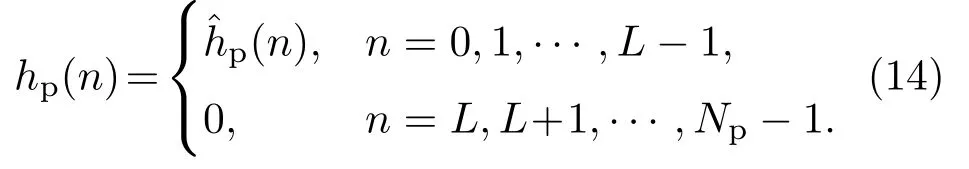
再对hp(n)做Np点的DFT，最后得到降噪后导频处信道响应估值为

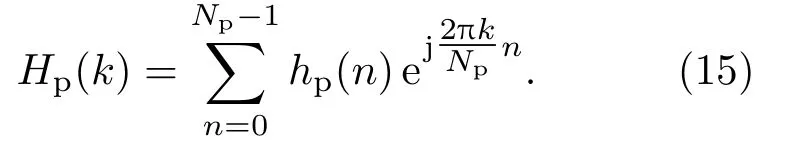
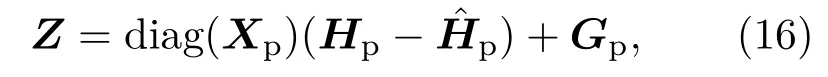
其中，Hp、分别表示导频处Np×1 维信道频响的真实值及LS 估计值。再令d=Hp−，则式(16)变为式Z= diag(Xp)d+Gp，可假设噪声Z为均值为0 的多变量正态分布，其协方差矩阵可表示为

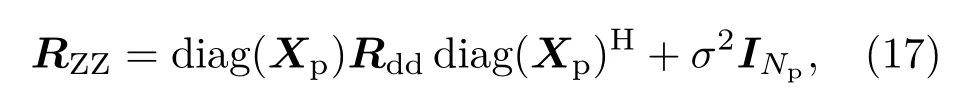
其中，σ2表示高斯噪声的方差，可根据LS 信道估计获得估值，Rdd表示d的协方差矩阵，由式(18)计算：

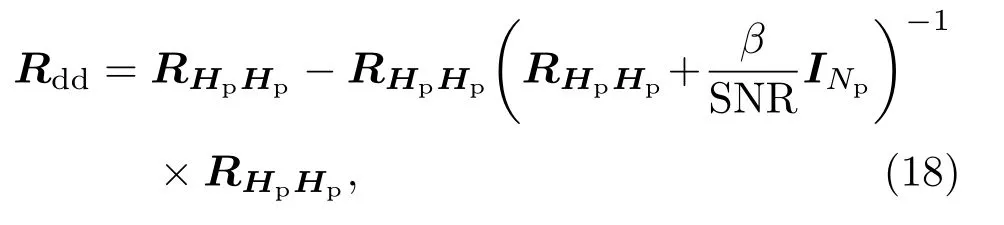
其中，β是常数，其取值与具体的调制方式有关，SNR 表示信噪比，INp表法Np×Np维单位矩阵。RHpHp表示导频处的Np×Np维信道自相关矩阵，由于信道自相关矩阵获取较为困难，本文在LS算法的基础上对采用DFT 变换域降噪处理后得到Hp，进而得到近似自相关矩阵RHpHp。由式(17)可计算以下各式：

其中，trace(·)表示对矩阵求迹，RZZ(i,j)表示矩阵RZZ的第i行第j列位置的元素。再由式(19)和式(20)计算∥Z∥22的标准差

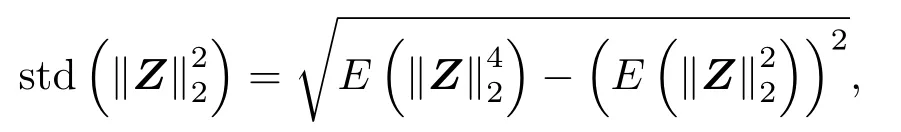
根据概率论知识，∥Z∥22一般情况下满足[9]

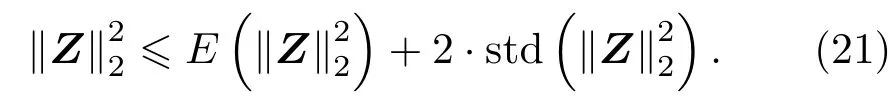
综上，由式(21)可近似得到误差容忍值ε：

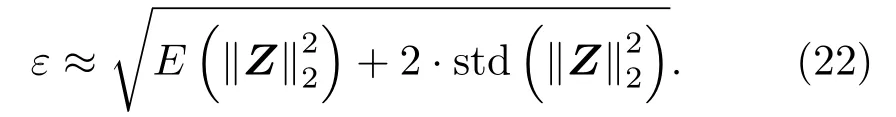
2.3 信道响应及限幅噪声估计的进一步优化

由于式(15)信道响应估计的初值并没有考虑限幅噪声的影响，因而这个信道响应还需进一步提高精确度，式(6)得到后，可利用接收到的Y和进行信道频响估值的优化计算：

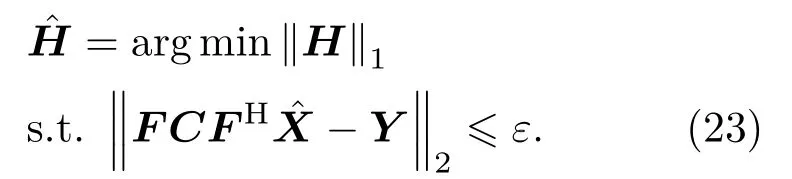
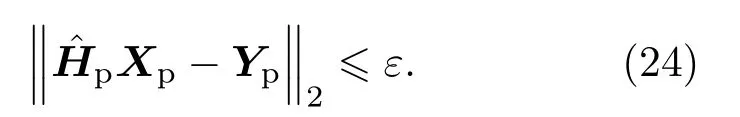
综上所述，可将以上对于稀疏限幅噪声的估计及消除限幅失真和信道估计优化的算法，用一个系统原理图表示，如图1所示，可以更加明了本文所提算法的具体流程。

图1 CS 补偿限幅噪声及信道估计优化原理图Fig.1 Principle diagram of optimizing clipping noise and channel estimation

3 仿真分析

下面通过计算机仿真验证上述峰均比非线性失真CS 补偿与LS 信道估计相结合的优化算法，由于水声信道较为复杂，为了独立分析新算法的性能，本文的仿真过程首先考虑多径水声信道加性高斯白噪声的作用，然后再考虑多普勒效应的影响。系统仿真参数详细说明参见表1[10]，直接限幅PAPR 门限设为10 dB，调制方式为8-QAM，星座图功率归一化因子β= 9/8。仿真使用单频正弦信号作为发射信号，经过5条路径传播，幅度衰减和相对时延差如表2所示[11]，仿真过程将利用互补累积分布函数(Complementary cumulative distribution function, CCDF)，误码率(Bit errors rate, BER)及星座图来分析本文优化算法的性能。

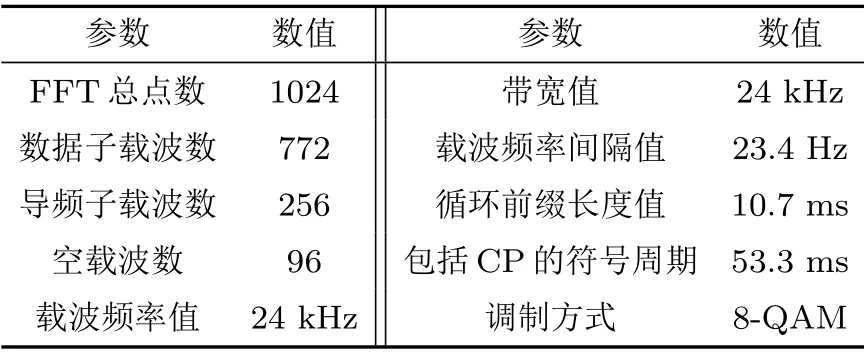
表1 OFDM 系统参数Table 1 OFDM system parameters

首先分析验证CS 算法对PAPR 非线性失真的补偿效果。利用表1、表2中的数据，图2绘出了直接限幅法、压缩扩展法的CCDF 曲线的对比仿真结果。由于CS 算法主要对直接限幅法的非线性失真进行补偿，所以在CCDF 曲线上只能用直接限幅的曲线来体现，而CS 算法的补偿效果主要体现在图3中，图3分别绘出了CS 限幅补偿算法、压缩扩展限幅和直接限幅算法的BER 曲线。由于压缩扩展限幅和直接限幅算法不能去除接收端的限幅噪声，因而使得这两种方法虽然能保证水下HPA 正常工作，对PAPR 的抑制作用非常有效，但却不能保证系统的误码率性能。从图3的误码率曲线可以看出，CS算法很好地补偿了直接限幅的非线性失真，获得了比压缩扩展法更好的系统性能。

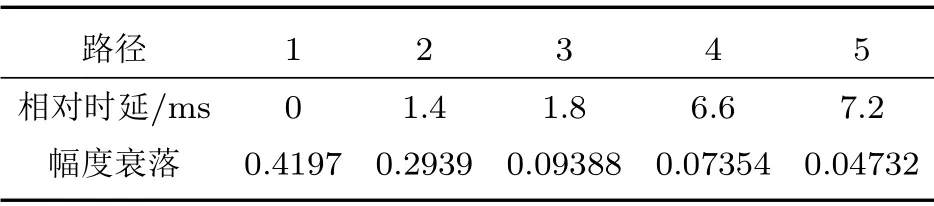
表2 水声信道多径幅度衰落和相对时延Table 2 Multipath amplitude fading and relative delay of underwater acoustic channel

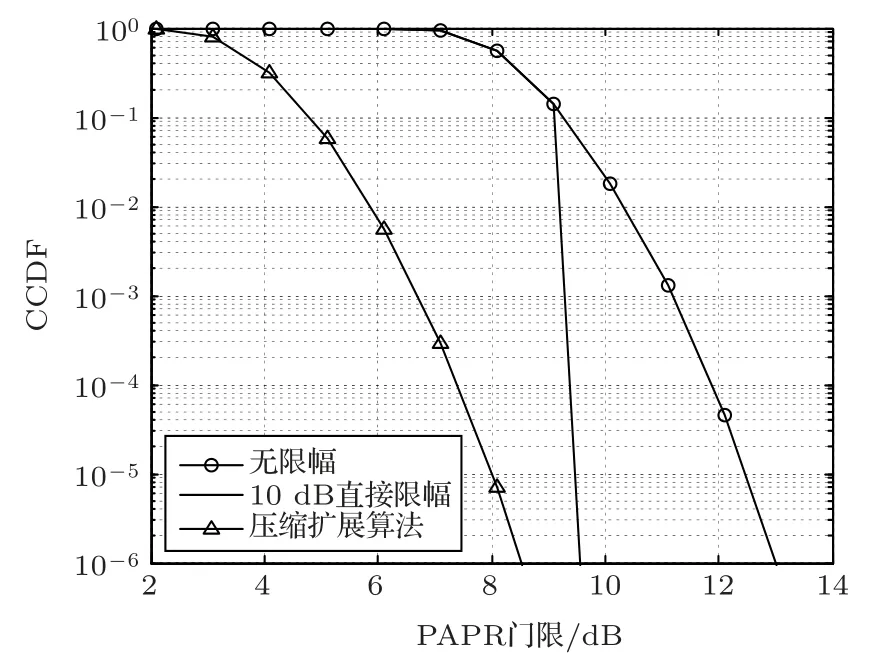
图2 PAPR 限幅算法的CCDF 比较Fig.2 CCDF comparison of PAPR clipping

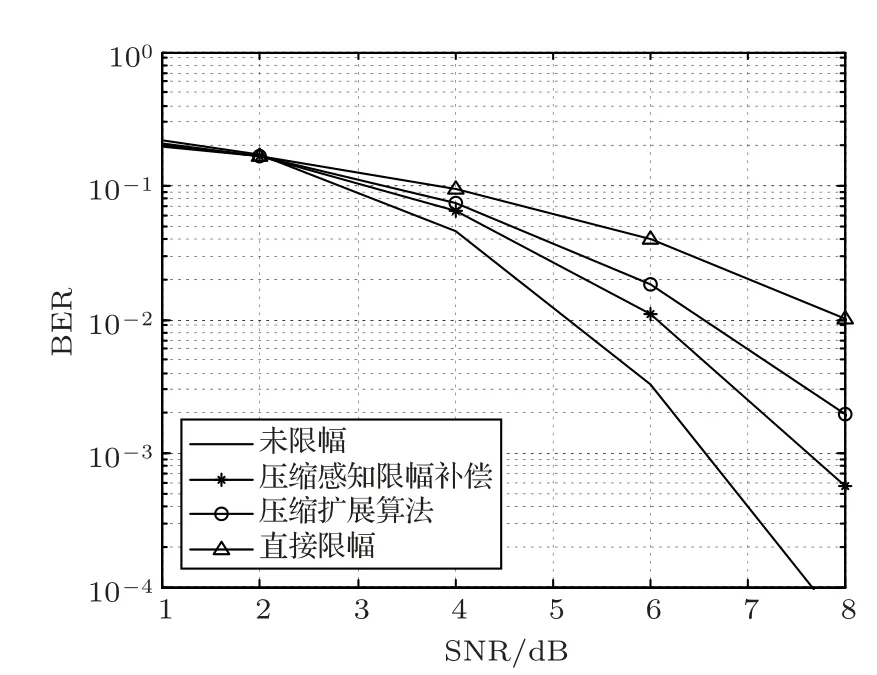
图3 PAPR 限幅算法的BER 比较Fig.3 BER comparison of PAPR clipping

另外，为了和其他类别的降低PAPR 的方法相比较，下面将传统的概率类算法中的选择性映射(Selected mapping, SLM)法、部分传输序列(Partial transmit sequence,PTS)法与直接限幅结合CS补偿算法进行CCDF 曲线及BER 曲线的性能对比仿真分析。将SLM 算法中的传输序列数目设为4，将PTS 算法中的相位加权系数(旋转因子)的数量也设为4。图4给出了直接限幅法、SLM算法及PTS算法的CCDF 曲线，如果只考虑对于PAPR 的抑制作用，从图4中可以看出，PTS 方法要稍好于SLM方法。图5给出了CS补偿法、SLM算法及PTS算法的BER曲线，从图5中可知，CS限幅补偿法的BER性能略好于SLM 算法及PTS 算法，但从上文所提的算法过程可知，CS算法在计算量及对信道估计的优化性能方面要好于概率类算法。

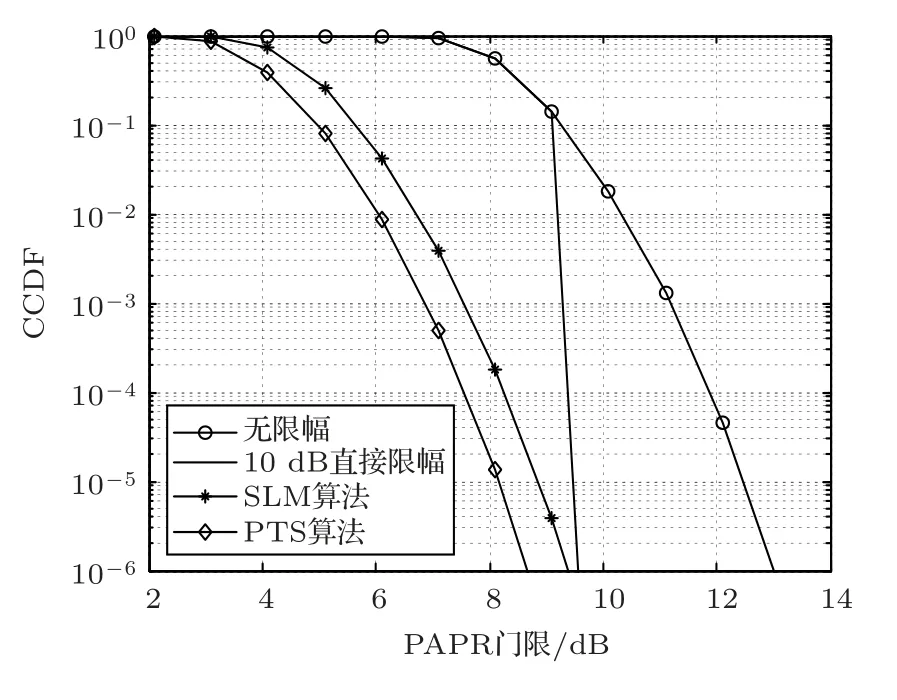
图4 PAPR 限幅与概率类算法的CCDF 比较Fig.4 CCDF of clipping and probabilistic algorithms

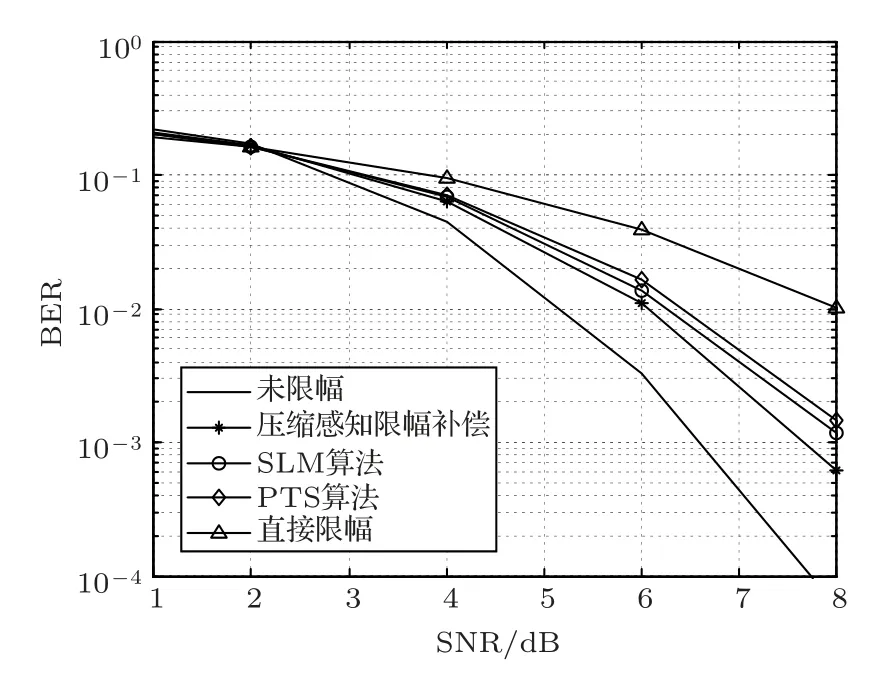
图5 PAPR 限幅与概率类算法的BER 比较Fig.5 BER of clipping and probabilistic algorithms

由于本文利用导频数据结合CS 的BP 算法进行限幅噪声的补偿运算，因此导频数据量的多少必然对本文的新算法有所影响。下面将针对不同导频子载波间隔对系统性能的影响，利用BER曲线进行仿真对比分析。从图6中可以看出，随着导频间隔的增大，系统性能会有所下降，这主要是因为导频间隔对信道估计LS算法有较大影响，从而会影响误差阈值ε的判断。

图6 不同导频子载波数系统BER 比较Fig.6 BER comparison of different pilot number

另外，为了验证多普勒效应对于新算法的影响，下面采用BER曲线的形式进行仿真分析。在表1及表2仿真参数的基础上，设多普勒因子为0.01，先是对于系统不加任何的多普勒频移的补偿算法进行仿真分析，然后再用传统的时域块估计方法对普勒频移进行估计和补偿后进行仿真对比。由图7仿真结果可知，多普勒频移对于新算法的影响较大，这主要是因为信道估计受多普勒影响较为严重。

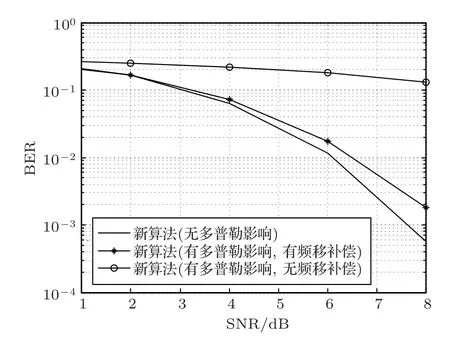
图7 多普勒效应对于新算法的影响Fig.7 Influence of Doppler effect on new algorithm

由于单一的基于CS 的限幅失真补偿算法受信道估计的影响较大，本文采用的CS 与LS 信道估计相结合的优化算法，可以在减小限幅失真的同时提高信道估计性能。图8(a)、图8(b)及图8(c)分别从无限幅补偿、CS限幅补偿及CS限幅补偿与LS信道估计优化组合算法3 个方面，利用星座图进行仿真对比分析。从仿真图中可知，不做任何补偿运算的限幅操作会产生很大的失真，而单一的CS 的限幅失真补偿算法能够在一定程度上减小限幅失真，较为理想的情况是采用CS 限幅失真补偿与LS 信道估计相结合的优化算法，如图8(c)所示。

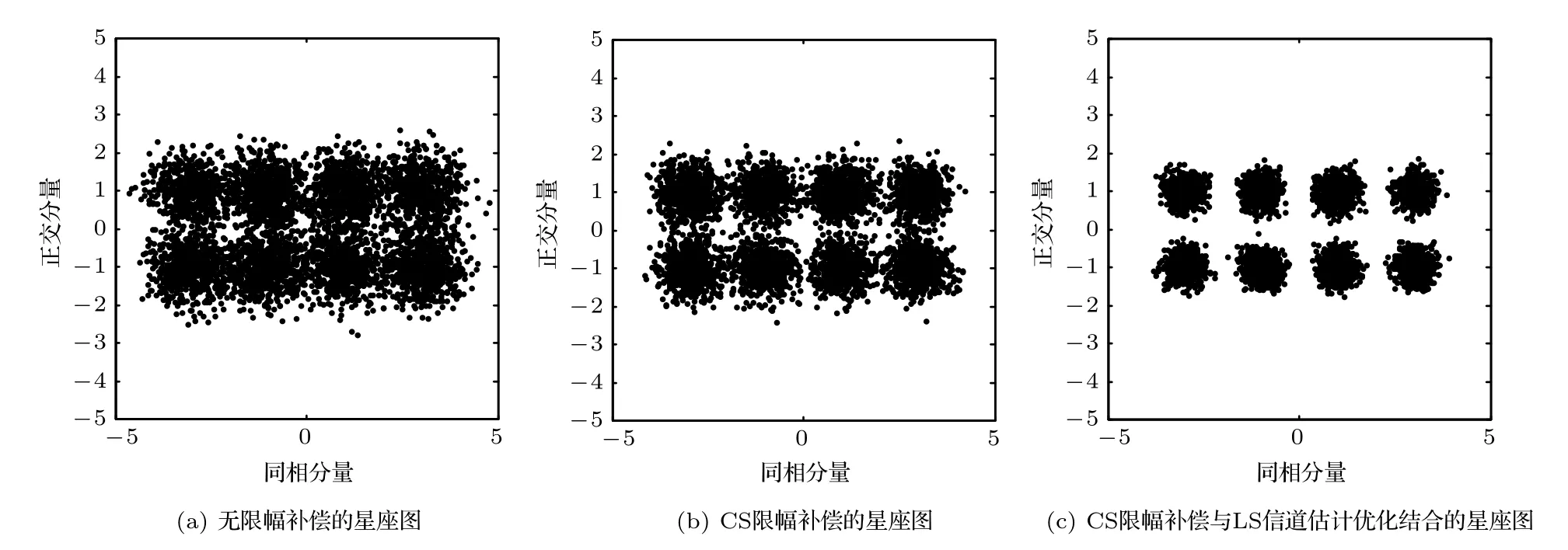
图8 CS 限幅补偿与LS 信道估计优化算法星座图Fig.8 Constellation of optimizing clipping noise and channel estimation

4 结论

本文采用CS 与导频数据相给合的限幅噪声的估计及补偿算法，使接收机能够有效恢复信号限幅前的幅值，同时减小噪声对于LS 算法的影响。主要根据水声信道中限幅脉冲噪声的稀疏特性，基于CS处理算法，再结合信道估计LS优化算法，在提高HPA工作效率的同时，能够有效降低限幅噪声和信道估计噪声，从而使整个系统性能得到提升。算法构建过程及计算机仿真分析结果均表明，CS算法对于降低限幅噪声具有较为明显的提升作用，而且运算复杂度较低。综合以上理论及仿真分析结果可知，本文提出的基于CS 的OFDM水声通信系统PAPR的抑制及补偿与LS信道估计优化相结合的算法，能够有效提高OFDM水声通信系统的性能。