动态条件下超声储层水敏性去除实验研究∗

华 强

(濮阳职业技术学院 濮阳 457000)

0 引言

储层渗透率是一定压差下，岩石允许流体通过能力的直接反映。储层渗透率的大小对油井的产量、水井的注入量有重要影响。当注入水等外来流体进入储层，由于不配伍性等问题引起黏土矿物膨胀、储层孔喉堵塞从而导致储层物性损害的过程即储层水敏性伤害。在石油开采过程中，储层水敏性问题会导致储层物性伤害，影响油田开发效果。储层水敏性是造成储层渗透率伤害的重要因素。

超声是一种绿色、环保技术，对水敏性去除有一定的效果。目前，国内外学者针对超声去除储层水敏性展开了研究。Wang 等[1]设计静态实验，展开了超声-化学剂联合去除储层水敏性研究，认为超声最佳处理频率为20∼25 kHz，且增大超声功率有利于岩心水敏性的去除，证明了超声波与化学剂的协同效应；Khan 等[2]给出了超声最佳处理时间为100 min，此时渗透率恢复率可达24.4%，超过这一处理时间，渗透率恢复率逐渐减小。

上述研究证明了超声技术对于储层水敏性伤害所致的渗透率损失有一定的去除效果。然而，前人对于该技术的研究多侧重于静态研究及小功率超声的应用，对于动态过程中超声水敏性的去除缺乏充足的认识，不同物性、高频超声对储层水敏性去除规律尚不清楚，而这些问题对于了解超声作用提高水敏性去除的作用机理具有重要的意义。

因此，基于现有研究的不足，本文设计动态超声波储层水敏性去除实验，采用不同渗透率的天然岩心和大功率超声对此进行探讨，研究了在流动状态下超声去除水敏性的影响因素，以期进一步夯实超声去除水敏性伤害的理论基础，并为推广该技术在油田现场的应用提供理论指导。

1 动态超声波储层水敏性去除实验

为进一步揭示动态过程中超声对储层水敏性去除的作用机理，利用自主研制的超声发生仪，选取不同渗透率的天然岩心，模拟实际地层的温度、压力，在不同的超声作用参数下进行室内驱替实验。

1.1 实验设备及材料

1.1.1 实验设备

(1)岩心驱替实验装置：设备型号为HKY-20C，最大驱替压力40 MPa，环压0∼50 MPa，流量范围0.01∼10 mL/min，工作温度0◦C∼150◦C，主要由注入系统、夹持器系统、计量系统、数据采集与处理系统等组成，该设备用于动态条件下的岩心渗透率测定。

(2)超声发生仪：使用濮阳市物理法采油重点实验室自主设计研制的超声发生仪，设备型号为US-GDS-1036A，由超声发生器、固定支架、超级恒温水浴以及显示器组成。工作频率为17∼125 kHz，最大输出电功率2000 W，超声设备的超声作用面积为20 cm×30 cm，运行温度为10◦C∼110◦C，加载方式为连续型，可满足长时间的使用要求。超声波声强测试仪器采用本多HONDA HUS-3。图1为功率为1200 W的超声波不同频率下的声压变化。

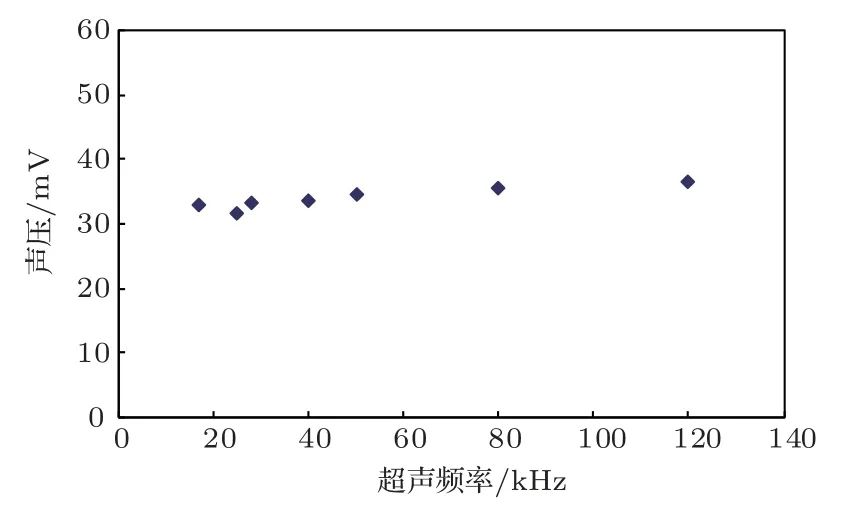
图1 声压与频率关系Fig.1 The relationship between sound pressureand frequency

(3)岩心气测渗透率仪：设备型号为STY-2，测试岩心直径为25 mm，测试岩心长度为20∼70 mm，工作介质为氮气，低渗测量差10%。

(4)电子分析天平：设备型号为力辰FA124，精度0.1 mg。

1.1.2 实验材料

实验岩心样品采用中原油田的天然岩心，岩心直径为(2.5±0.1)cm，长度为3.1∼7.5 cm，渗透率为11×10−3∼1423×10−3µm2；考虑到中原油田储层特点，本次研究采用的模拟地层水矿化度为20000 mg/L，组分配比NaCl :CaCl2:MgCl26H2O=7.0:0.6:0.4。

1.2 实验步骤

(1)将岩心样品进行编号、清洗并置于50◦C烘箱烘干24 h，测试岩心的基本参数(气测渗透率、孔隙度)。

(2)将岩心饱和模拟地层水后，将其放入岩心夹持器，加环压，开泵水驱。为消除温度变化和速敏对实验结果的不利影响，在实验温度为70◦C 的条件下，采用泵入速度小于临界流速，模拟地层水泵入速度设定为0.02 mL/min，流动稳定后，利用达西定律计算岩心的初始渗透率(Ki)，直至注入2 PV(PV为注入孔隙体积倍数，无因次)。

(3)将模拟地层水改变为蒸馏水，速度设定为0.02 mL/min，稳定后计算岩心渗透率(Kb)，直至注入4 PV，建立储层水敏性伤害后的岩心。

(4)打开超声发生仪，测定超声作用后的岩心渗透率(Ka)。

(5)重复步骤(1)∼(4)，分别采用不同的超声波作用参数，以岩心渗透率恢复程度KR=(Ka −Kb)/Ki ×100%作为评价指标，研究各作用参数对储层水敏性伤害的恢复情况。

图2为实验流程示意图。

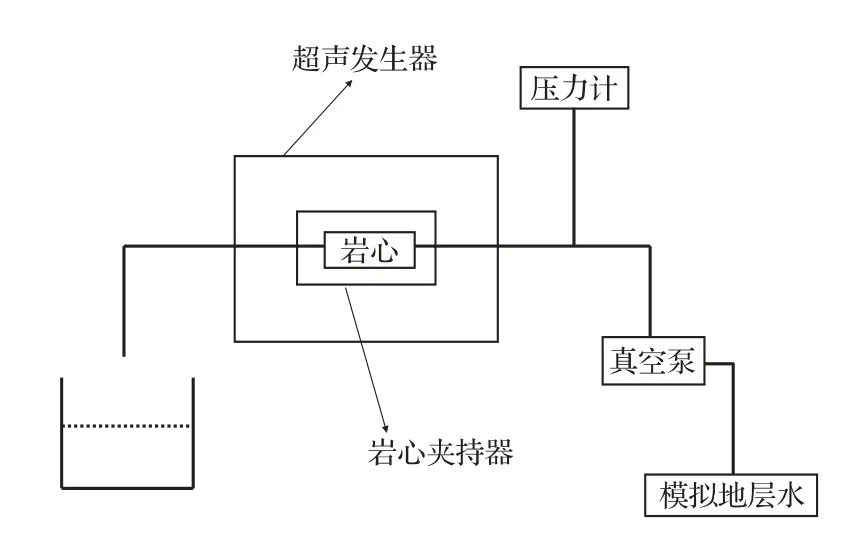
图2 实验流程示意图Fig.2 Experimental setup

2 实验结果与讨论

2.1 频率

研究中采用不同频率的超声波对天然岩心进行处理，分析超声频率对动态条件下储层水敏性去除的影响。实验中作用时间为20 min，功率为1200 W，岩心渗透率为56.36×10−3µm2。

通过研究发现，超声波的频率与储层渗透率恢复存在较为复杂的关系，见图3。当超声频率处在17∼22 kHz范围时，随着频率的增加，渗透率恢复率迅速增加；当超声频率处在22∼50 kHz 范围时，随着频率的增加，渗透率恢复率急剧减小；而当超声波频率超过50 kHz时，渗透率恢复率则呈缓慢上升趋势。

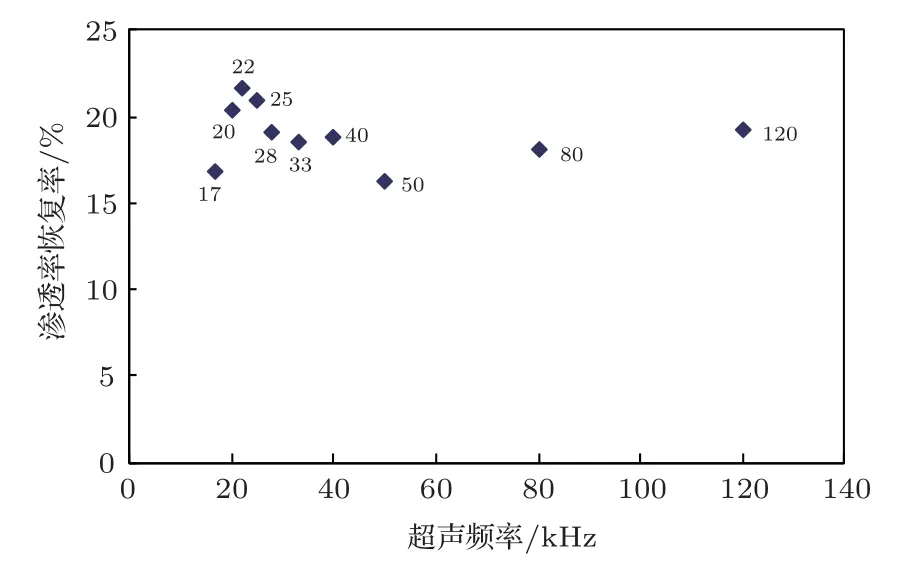
图3 频率与储层渗透率恢复率关系Fig.3 The relationship between frequency and reservoir permeability recovery

由于超声能量衰减随着频率的增加而变大[3]，较高的超声波频率不利于岩心水敏性伤害的去除，故应将频率控制在合理的范围内。当储层固有频率与超声波频率匹配时，能引起黏土矿物颗粒在储层孔隙内部的蠕动传输，对于降低储层水敏性伤害能取得良好的效果。在较低频率(17∼22 kHz)下，空化作用产生的空化泡具有数量较少、尺寸大、能量强的显著特点，所以在17∼22 kHz 频率范围内，渗透率恢复率处在较高的水平上。随着超声频率增加，超声能量迅速衰减，系统内空化作用产生的力学效应随超声波频率增大而降低，空化作用的减弱会促进黏土颗粒聚结的趋势[4]，这一点并不利于储层渗透率的恢复；但高频声波往往在介质中吸收更多，由此产生更强的边界摩擦作用，随之产生的热量往往会除去黏土的吸附水，导致黏土颗粒尺寸的减小，相邻黏土颗粒之间的空间逐渐变大。也就是说，超声作用通过减小黏土团簇的尺寸，从而促进储层内部黏土颗粒的悬浮程度，最终减少了储层的水敏性伤害，储层渗透率得以部分程度的恢复。水的存在填充了孔隙空间，影响了多孔介质里面的超声波传播特性[5−7]。高频声波对于渗透率恢复的影响取决于上述两种效应的作用强弱，在一定程度上，边界摩擦作用能间接地抑制黏土矿物在储存内部的水化膨胀和分散。

2.2 超声功率

前人研究多停留在较低功率超声对储层水敏性的去除，采用功率多低于1000 W，尚缺乏大功率超声对储层水敏性问题的相关研究，因此，特研制大功率超声发生器，开展相关研究。实验中超声作用频率分别25 kHz、50 kHz，超声作用时间为30 min，岩心渗透率为45.92×10−3µm2。

通过研究发现，超声波功率与储层渗透率恢复存在明显的正相关关系，见图4。当超声频率为25 kHz 时，渗透率恢复率随功率的变化一直保持增加的趋势，当超声功率高于1300 W 时，渗透率恢复率则保持相对稳定；而当超声波频率为50 kHz、超声功率低于1300 W 时，随着超声功率的增加，渗透率恢复率迅速增加；当超声功率高于1300 W 时，随着超声功率的增加，渗透率恢复率则保持相对稳定，不再继续增加。从实验结果来看，当采用较低的超声功率时，两种频率下的超声所对应的渗透率恢复率差值较大(500 W，差值为4.2%)；当采用较高的超声功率时，两种频率下的超声所对应的渗透率恢复率差值较小(1700 W，差值为1.7%)，说明大功率超声解除水敏性伤害具有更大的优势，在使用时不会受到频率的限制。

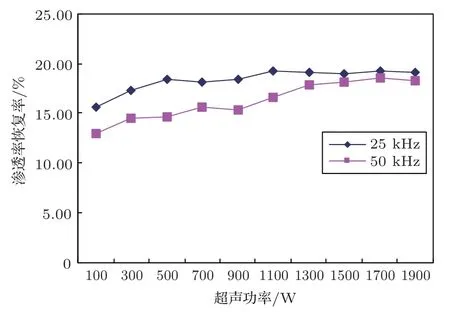
图4 超声功率与储层渗透率恢复率关系Fig.4 The relationship between ultrasonic power and reservoir permeability recovery

随着超声功率的增加，系统的能量供应越充足，超声空化作用就越强烈[8]，越有利于水敏性去除。提高超声波功率能够弥补频率增大所引起的超声波能量衰减。超声频率越高，能量衰减越大，这一点较好地解释了较高频率下渗透率恢复率小于较低频率下的渗透率恢复率这一现象。功率可补偿因频率引起的衰减。大功率的超声作用于油层时，储层内部的毛细管直径会随着超声作用时大时小，由于直径发生变化，表面张力、毛细管力均会随之发生变化，所以能获得更高的渗透率恢复率。

2.3 作用时间

超声最佳激励时间研究处于起步阶段，为研究超声波处理时间对去除岩心水敏性的影响规律，开展相关实验。实验中超声频率为25 kHz，功率为1000 W。为增强其代表性，采用3 种不同的岩心，岩心1渗透率K1=16.55×10−3µm2，代表低渗储层；岩心2 渗透率K2= 133.23×10−3µm2，代表中渗储层；岩心3 渗透率K3= 1265.79×10−3µm2，代表高渗储层。

研究发现，在超声波作用初期，3 种岩心的渗透率恢复率迅速增加，呈现相似的特征，高渗储层的曲线斜率明显高于中渗、低渗储层，说明原始渗透率越好的储层，其渗透率恢复速度也越快，见图5。不同的是，低渗岩心的渗透率恢复率在超声作用100 min 后达到最高值，之后增加超声处理时间，渗透率恢复率基本保持平稳，这一结果与文献[2]较为吻合；中渗岩心的渗透率恢复率在超声作用80 min后达到最高值，之后基本保持平稳；对于高渗岩心，该处理时间缩减为60 min，中渗、高渗岩心对应的超声处理时间均小于文献[2]研究结果。这说明，渗透率更低的岩心应采用更长的超声激励时间，超声处理存在一个最佳处理时间，且这一最佳处理时间与储层物性密切相关，储层物性越好，最佳处理时间越短，过长的超声激励时间有可能导致较大颗粒分离[2]，这些颗粒在后面以架桥的形式阻碍流体的渗流，导致渗透率恢复率降低。

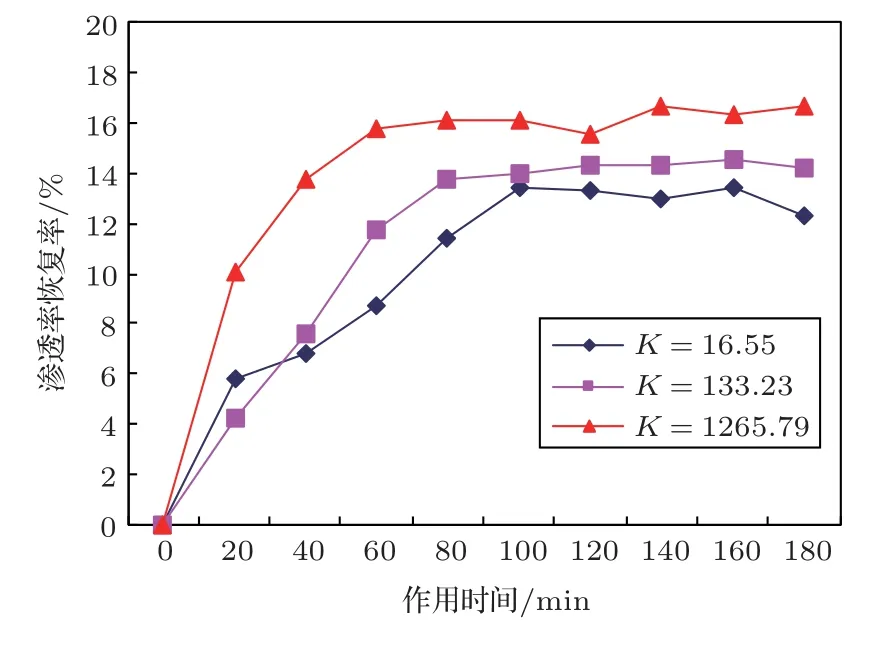
图5 作用时间与储层渗透率恢复率关系Fig.5 The relationship between action time and reservoir permeability recovery

超声处理存在最佳处理时间，这与文献[1]的研究较为吻合。与其不同的是，本文研究发现，最佳处理时间与储层物性密切相关，分析其原因，在于文献开展的实验为静态实验，流体对超声能量的吸收程度不同；另外，文献[1]开展的实验采用岩心的渗透率为30×10−3µm2、60×10−3µm2、120×10−3µm2，岩心属于中低渗范围，岩心物性相差不大，所以超声处理时间的差别并不明显。

低渗储层孔喉半径较小，黏土颗粒与孔喉内壁的距离较小，致使孔喉内壁对黏土颗粒产生较强的吸附作用；加之低渗储层易受污染，所以低渗储层需要较长的处理时间。但是，对渗透率为16.55×10−3µm2的岩心1 累积处理时间达到180 min时，渗透率恢复率降低了1.1%，这是由于长时间的超声作用造成岩心入口端强烈的空化作用，作用在岩心的超声能量减少，从而导致较多的声能量逸散；另外，空化泡湮灭时产生的压力给岩心驱替系统施加了回压效应，导致流体流动受阻，这种回压对于物性差的低渗岩心影响更显著。

2.4 储层渗透率

文献[1–2]分别使用渗透率30×10−3∼150×10−3µm2的3种岩心开展实验，使用的渗透率范围过于狭窄，不能充分揭示渗透率对水敏性解除的真实影响，这一影响并没有得到充分的探讨。因此，为更全面地揭示储层渗透率与渗透率恢复率之间的内在联系，尤其是探索中高渗储层的渗透率恢复问题，本次研究采用中原油田23 块天然岩心(渗透率范围11×10−3∼1423×10−3µm2，低渗、中渗、高渗储层都有涉及)，进行更加系统的研究。

通过研究发现， 当储层渗透率低于30×10−3µm2时，渗透率恢复率处在较低的水平；当储层渗透率处在30×10−3∼80×10−3µm2范围时，随着渗透率的增加，渗透率恢复率逐渐增大；而当储层渗透率高于80×10−3µm2时，则呈现出中渗储层渗透率恢复率逐渐增大而高渗储层渗透率恢复率相对稳定的特征，见图6。

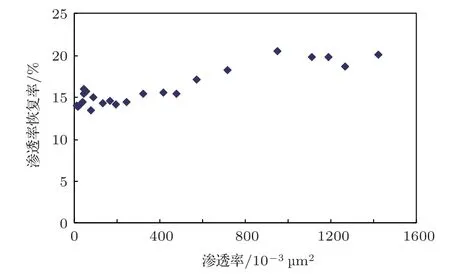
图6 储层渗透率与储层渗透率恢复率关系Fig.6 The relationship between permeability and reservoir permeability recovery

当储层渗透率较高时，储存的孔喉直径较大，黏土颗粒与孔隙内壁的作用力较小，在超声波作用下，黏土颗粒更容易摆脱储层内壁对其吸引力而脱落，渗透率恢复率随渗透率的增大而增大。在油气层渗流中，黏土颗粒的水敏性膨胀降低了孔喉的有效直径，从而增大了渗流阻力，造成了水敏性伤害这一严重后果，黏土颗粒的水化膨胀会造成储层的水敏性伤害。

3 结论

通过实验发现，超声频率对于去除储层水敏性存在最佳范围，为17∼22 kHz。当超声频率处在22∼50 kHz范围时，随着频率的增加，渗透率恢复率急剧减小；而当超声波频率超过50 kHz，渗透率恢复率则呈缓慢上升趋势。超声频率与功率存在一定的补偿关系，现场应用需重视频率、功率的匹配问题。超声最佳处理时间与储层物性有一定联系，不同渗透率的储层超声最佳处理时间有明显差异。渗透率恢复率与储层物性呈现较复杂的关系。研究结果有助于了解超声水敏性去除的作用机理，为该技术在油田现场的推广提供理论指导。