一种高灵敏度的桥型声表面波应变传感器∗

李鹏旭 李红浪 程利娜 卢孜筱 罗 为 刘久玲

(1 中国科学院声学研究所 北京 100190)

(2 国家纳米科学中心 北京 100190)

(3 中国科学院大学 北京 100049)

(4 华中科技大学 武汉 430074)

0 引言

城市燃气管道[1]、叶轮[2]等设备容易受到自身重力或外力作用影响而发生异常形变，实时进行高灵敏度的形变监测并准确定位发生形变异常的高风险点，能够及时排除潜在故障，保障设备的安全性。声表面波(Surface acoustic wave, SAW)应变传感器因无线无源、精度高、功耗低、灵敏度高等优势在上述结构监测中表现出了较高的应用价值[3]。

为了提高SAW 应变传感器的应变灵敏度，国内外研究者做了多方面研究。Oh 等[4]从压电基片切向方面对SAW应变传感器应变灵敏度做了研究，通过改变压电基片的切向，采用水平剪切(Shear horizontal, SH)波模式使SAW 应变传感器的应变灵敏度提高了15%；Maskay 等[5]研究报道了传感器的安装位置对应变灵敏度的影响，当SAW 的传播方向平行于梁的纵轴时，所对应的应变灵敏度最高；Kalinin 等[6]采用全石英的封装以减少传统金属封装粘接层对应变灵敏度的影响；Ren 等[7]通过刻蚀将LiNbO3基片中心谐振器区域减薄来提高应变灵敏度。上述研究者主要从器件切向设计、传感器安装方式、粘接层影响、器件结构设计工艺等方面提高传感器的应变灵敏度，而从应变分布规律出发设计合理的结构以提高SAW 应变传感器应变灵敏度未见相关报道。

本文根据待测构件受压弯曲情况下的应变分布特点提出一种桥型SAW 应变传感器以提高应变灵敏度。首先建立了桥型SAW 应变传感器的有限元模型，结合微扰法分析桥型结构几何参数对SAW传感器应变灵敏度的影响，根据分析结果确定了桥型结构几何参数并与传统SAW 应变传感器的应变灵敏度进行了对比，最后搭建受压弯曲微动实验平台，对桥型SAW 应变传感器和传统SAW 应变传感器的应变灵敏度进行了测试分析。

1 理论分析

1.1 结构介绍

桥型SAW 应变传感器的模型如图1(a)所示。整个传感器是由一个中心频率为433 MHz 的SAW应变传感器和两个石英立柱及黏合剂组成，石英立柱是和压电基片材质完全相同的石英晶体。与如图1(b)所示的传统SAW 应变传感器相比，桥型SAW应变传感器增加了两个石英立柱，石英立柱与基片用黏合剂连接。传统SAW 应变传感器与桥型结构传感器与待测构件均用黏合剂连接。

图1 两种结构SAW 应变传感器模型Fig.1 Two models of SAW strain sensor structures

当施加向下弯曲的载荷时，待测构件受压变形，如图2所示，在弯曲力矩的作用下中性层内侧材料受剪切应力压缩而变短，中性层外侧材料受剪切应力拉伸而变长。假设与中性层相距为y处的材料在弯曲形变后的长度由C1C2变为C11C12，根据弹塑性形变原理，其应变为[8]

图2 受压弯曲条件下桥型SAW 应变传感器形变示意图Fig.2 Deformation diagram of bridge SAW strain sensor under compression and bending

式(1)中，y为指定点到中性层的距离，K=1/R为中性层曲率。由公式(1)可知，在曲率固定情况下，指定点y距离中性层的距离越远，发生的形变越大，对应的应变值越大。根据此力学特征可知，待测构件发生弯曲形变，桥型传感器由于立柱的存在使得石英基片与中性层距离增大，产生的形变更大，与传统传感器与待测构件直接粘接相比，基片表面的形变引起电极间距、声波传播速度变化等也会变大，即SAW 的谐振频率会由于形变增大而产生更大的偏移量[9]。

1.2 应变灵敏度分析

为了实现对桥型SAW 应变传感器的应变灵敏度分析，采用微扰理论建立外界扰动和传感器应变灵敏度Ssen之间的关系[10]：

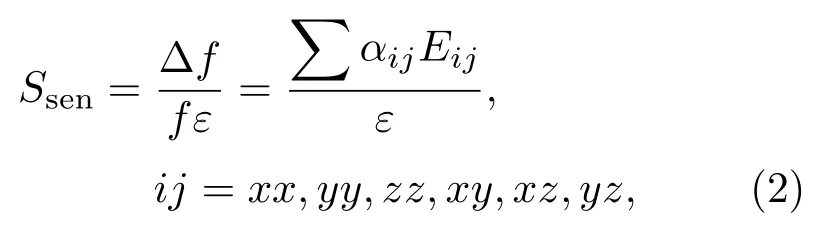
其中，f为无扰动时传感器的谐振频率，∆f为在应变ε作用下传感器的频率偏移量，Eij为6 个方向的应变张量，αij为各个应变张量对应的应变系数，这组系数仅取决于压电基片的材料参数，表征应变分量的敏感特性，应变系数αij利用微扰理论求解得到[11]，Y34◦切向的石英基片6 个方向的应变系数见表1。应变张量Eij通过有限元仿真方法得到[1]。

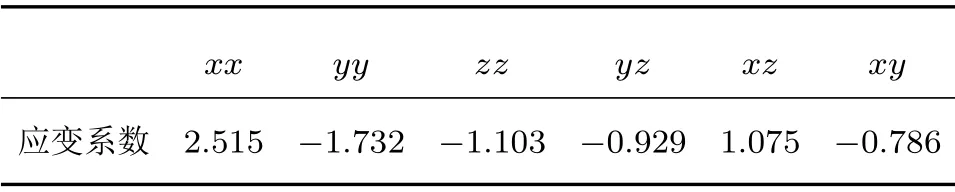
表1 Y34◦切向石英基片的应变系数Table 1 Strain coefficient of Y34◦ cut quartz substrate

首先构建如图3(a)所示的桥型SAW 应变传感器三维有限元仿真模型[12]，待测构件与传感器之间采用的黏合剂为结构硬胶，各部分材料参数见表2。

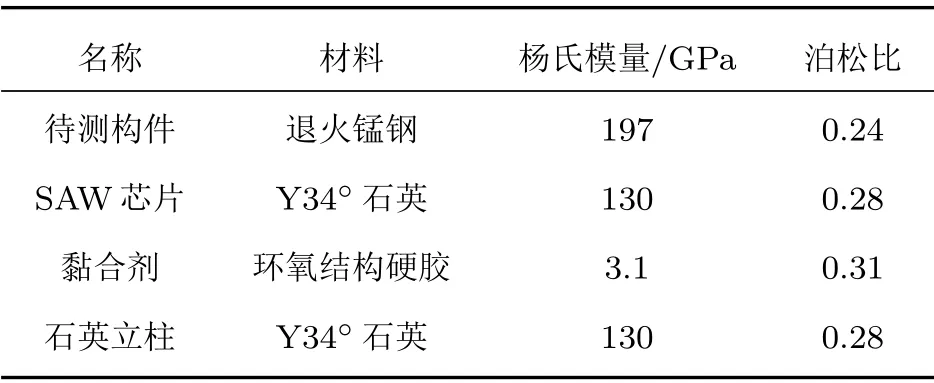
表2 有限元仿真中各部分材料参数Table 2 Explanation of material parameters of each part in finite element simulation

图3 两种SAW 应变传感器三维有限元仿真模型Fig.3 Two three-dimensional finite element simulation models of SAW strain sensors

待测构件的一端为固定边界条件，另一端施加z方向边界载荷，使得整个待测构件受压弯曲。首先对黏合剂的厚度Ta进行参数化扫描，有限元仿真得到不同黏合层厚度下谐振器表面的应变张量，结合微扰理论求解得到的应变系数，应变灵敏度分析结果如图4所示。结果表明，黏合剂厚度越薄，桥型SAW 传感器的应变灵敏度越高，故在保证黏合剂粘接强度的前提下，尽量降低黏合剂厚度以保证高的应变灵敏度。考虑到工艺实现难度，选取Ta=0.03 mm作为黏合层的厚度。

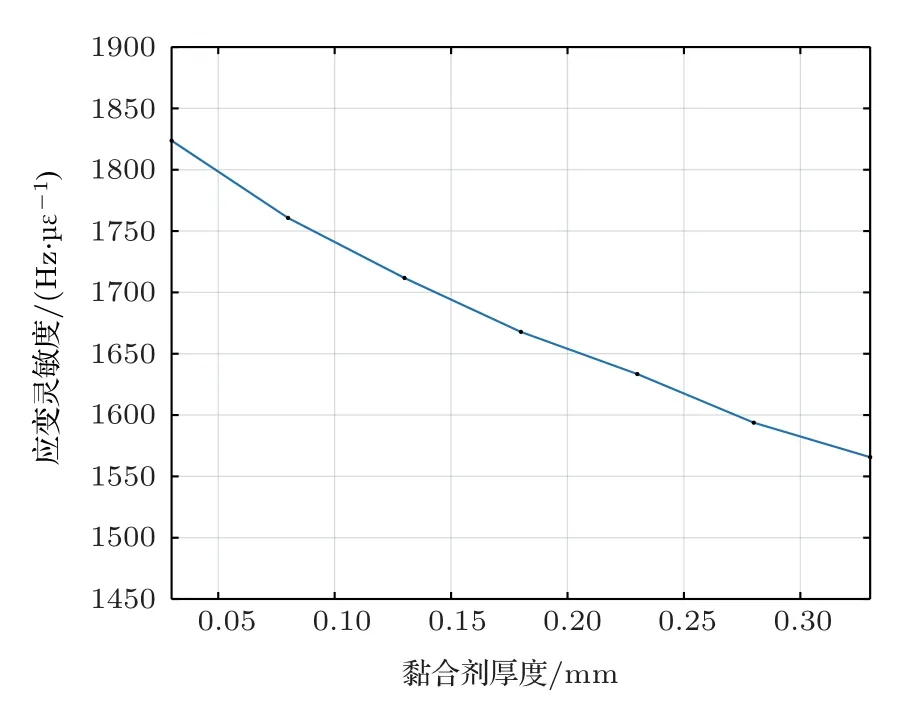
图4 桥型SAW 应变传感器黏合剂厚度对应变灵敏度的影响Fig.4 Influence of the adhesive thickness of bridge SAW strain sensor on strain sensitivity

固定黏合剂厚度Ta为0.03 mm，保证谐振器两侧边缘分别位于石英立柱内侧平面齐平，对图1(a)中石英立柱几何参数长度L、宽度W、高度T进行参数化扫描，桥型SAW 传感器的应变灵敏度随石英立柱几何参数的变化趋势如图5所示。

从图5可看出，石英立柱长度L和高度T变化对应变灵敏度的影响远大于立柱宽度W对灵敏度的影响。对立柱长度和高度两个参数对应变灵敏度的影响进行综合分析，结果如图6所示，应变灵敏度随着立柱长度的增加而增加后趋于平缓，在5∼10 mm 范围灵敏度增长率最高；应变灵敏度随立柱高度的增大呈先增大后减小趋势，且灵敏度最大值受立柱长度的影响，随立柱长度增大逐渐右移。

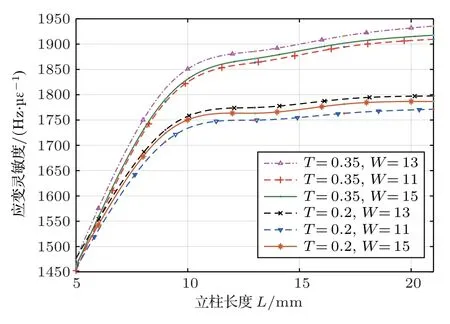
图5 桥型SAW 应变传感器几何参数对应变灵敏度的影响Fig.5 Influence of geometric parameters of bridge SAW strain sensor on strain sensitivity

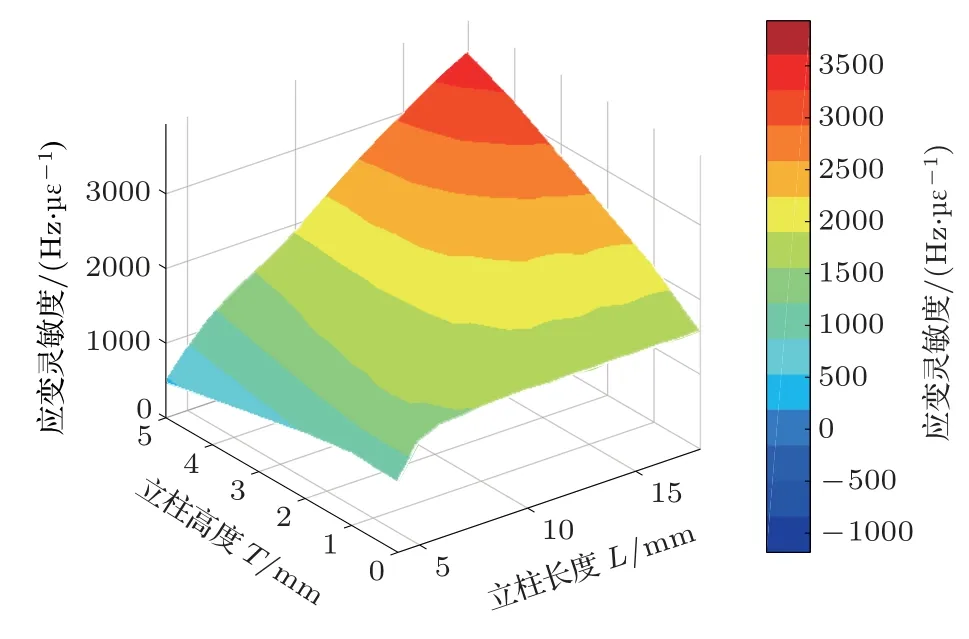
图6 桥型SAW 应变传感器立柱长度L 和立柱高度T 对应变灵敏度的影响Fig.6 Influence of the length L and thickness T of the bridge SAW strain sensor on the strain sensitivity

根据仿真结果并结合实验条件限制，选取L= 9 mm、W= 13 mm、T= 0.35 mm 作为桥型SAW 传感器结构的几何参数。构建如图3(a)、图3(b)所示的桥型SAW 应变传感器和传统SAW传感器的有限元仿真模型，对待测构件在z方向施加相同的应变，得到两种SAW 应变传感器基片表面的应变张量见表3。结合表2的应变系数，可得到中心频率为433 MHz的桥型SAW 应变传感器和传统SAW 应变传感器在主应变方向的应变灵敏度分别为1812.3 Hz/µε、1473 Hz/µε。

表3 两种SAW 应变传感器的应变张量Table 3 Strain tensor of two SAW strain sensors

2 实验验证

根据理论分析结果，本实验所采用的SAW 应变传感器中心频率为433 MHz，各部分的材料及几何参数如表4所示，采用水平式快速夹具严格控制黏合剂厚度，谐振器两侧边缘分别与桥型结构石英立柱内侧平面垂直齐平，制备桥型SAW 应变传感器。

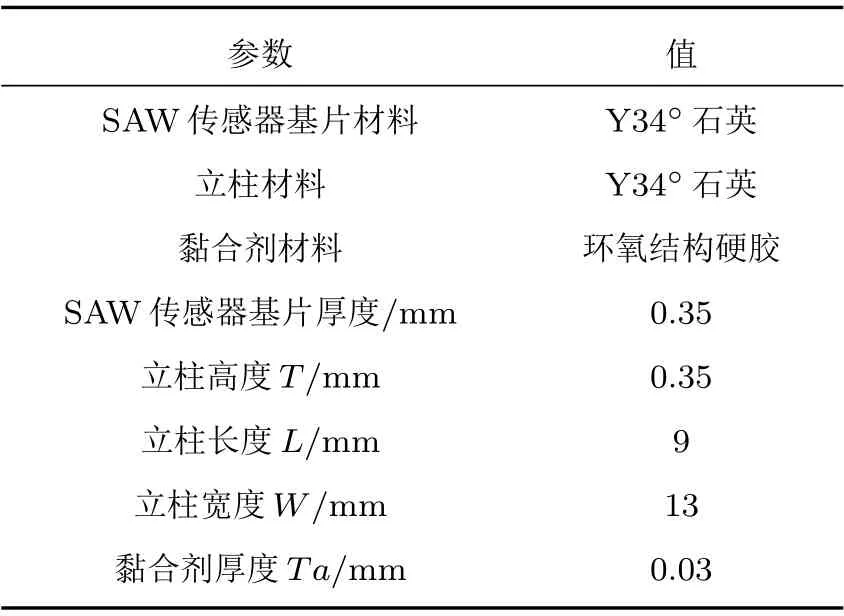
表4 桥型SAW 应变传感器的材料及几何参数Table 4 Material and geometric parameters of bridge SAW strain sensor

为了测试桥型SAW应变传感器的应变灵敏度，搭建了如图7所示的受压弯曲实验平台。整个平台包括微动台、不锈钢待测构件、传统SAW 应变传感器、桥型SAW 应变传感器、商用电阻应变片及相应的数据采集模块。在待测构件受压弯曲时曲率较大的同一高度[13]，按照如图7所示方式粘接3 组传感器进行应变感测。待测构件一端固定，另外一端施加z方向载荷使其产生弯曲变形，用网络分析仪采集传统SAW 应变传感器和桥型SAW 应变传感器的频率值，用应变仪模块采集应变值作为SAW 应变传感器的参考值。

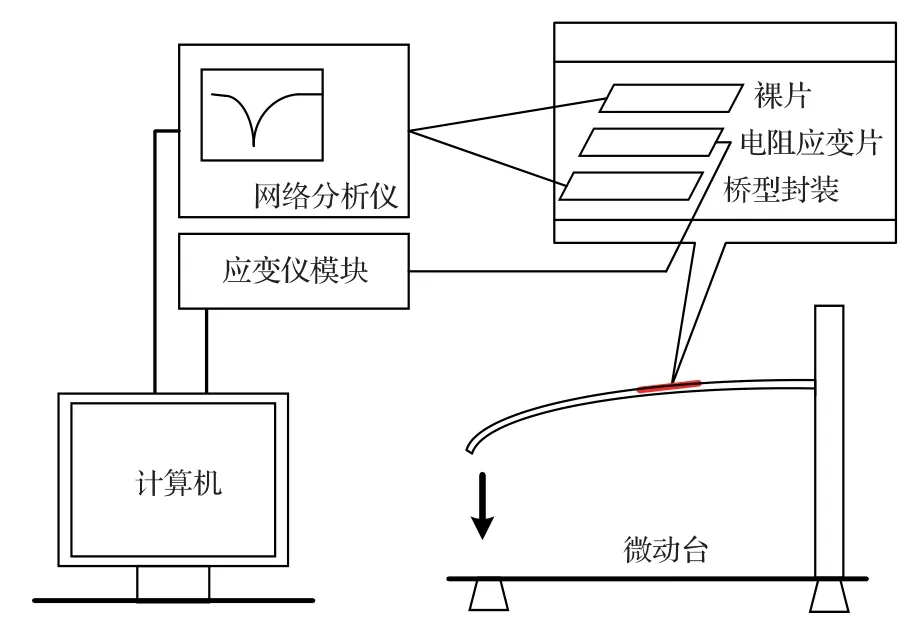
图7 SAW 应变传感器受压弯曲微动实验平台示意图Fig.7 Schematic diagram of SAW strain sensor compression bending micro-motion experimental platform

实验测得传统SAW 应变传感器和桥型SAW应变传感器的随应变变化的频率偏移数据如图8所示，拟合曲线如图9所示。

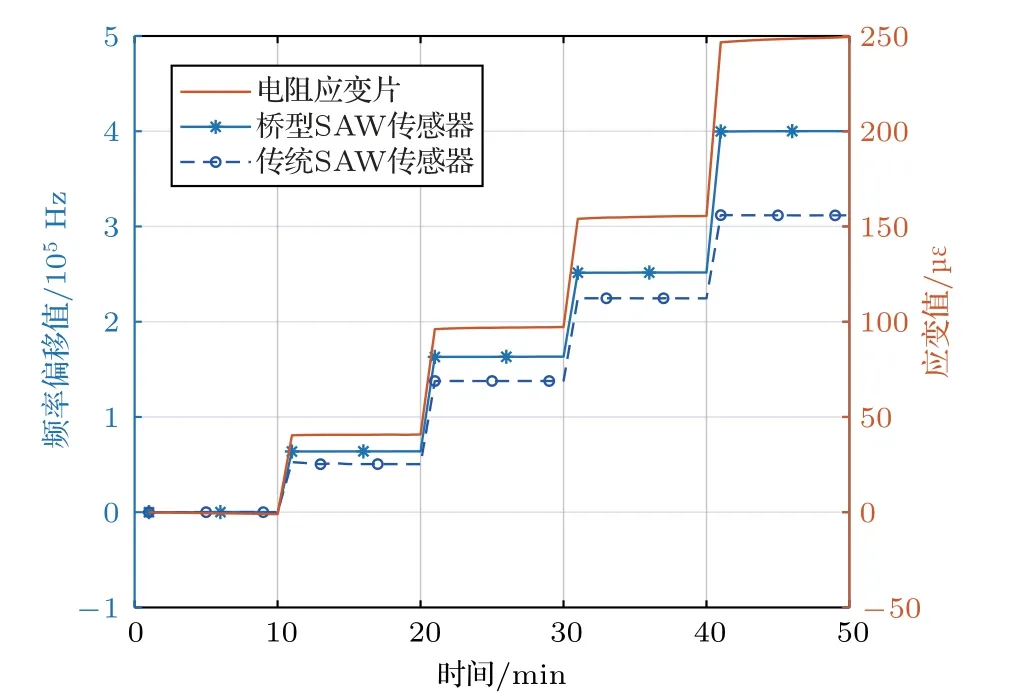
图8 商用电阻应变片及SAW 传感器应变测量值Fig.8 Strain measurement values of the commercial resistance strain gauge and SAW sensors

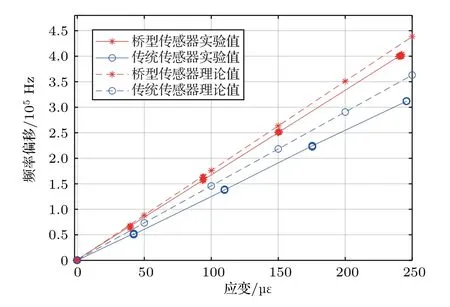
图9 传统和桥型SAW 应变传感器应变灵敏度拟合曲线Fig.9 Fitting curve of strain sensitivity of traditional and bridge SAW strain sensors

从拟合曲线可以得到桥型SAW 应变传感器的应变灵敏度为1692 Hz/µε，传统SAW 传感器的应变灵敏度为1328 Hz/µε，桥型结构比传统传感器应变灵敏度有明显提升。桥型和传统SAW 应变传感器所测得的应变灵敏度与理论分析相对吻合，灵敏度误差分别为7.1%、10.9%，存在误差的原因包括以下几点：黏合剂在粘接过程中厚度不能精确控制，实验与仿真的尺寸略有偏差；粘接后会存在不同程度的黏合剂溢出，对传感器的应变感知会有一定的影响；理论仿真中对黏合剂的材料参数考虑不全面，其硬度、固化程度、剪切强度等均会对应变灵敏度有影响，但在理论分析中难以仿真实现；实验平台中采集电路中引入的阻抗等均可能影响测试结果[14]。通过对误差因素来源的分析，下一步可以严格控制上述因素来提高测试的准确性，并实现对桥型SAW应变传感器其他各项性能指标的分析。

3 结论

本文提出一种桥型SAW 应变传感器以提高应变灵敏度。结合有限元法和微扰法对桥型SAW 传感器不同几何参数下的应变灵敏度进行了分析，结果表明立柱长度和高度对传感器的应变灵敏度有较大的影响，而立柱宽度对应变灵敏度的影响较小。对几何尺寸为L= 9 mm、W= 13 mm、T= 0.35 mm、Ta= 0.03 mm 的桥型SAW 传感器与传统SAW传感器的应变灵敏度进行理论分析，并设计实验对比研究了两种传感器的应变灵敏度。结果表明，直梁构件受压弯曲时桥型SAW 传感器的应变灵敏度为1692 Hz/µε，比传统SAW 传感器应变灵敏度提高了27.41%，为SAW 应变传感器的高灵敏度受压弯曲应变测量提供新思路。