基于地铁乘务资源共享的排班计划优化方法
2021-04-28金华陈绍宽王志美张翕然许凤志
金华,陈绍宽,王志美,张翕然,许凤志
(北京交通大学,交通运输部综合交通运输大数据应用技术交通运输行业重点实验室,北京100044)
0 引言
目前,地铁以分线独立运营为主,每条线路所属乘务员和乘务基地独立使用。本文提出的乘务资源共享是指列车不跨线运营情形下允许乘务员跨线值乘,即可在一个班次内值乘多条线路的值乘任务,同时允许乘务员选择乘务基地出退勤,以减少通勤时间。
基于资源共享的运营组织方法与技术已逐步受到关注,但仍亟待进一步深化[1]。既有资源共享研究多集中在车辆基地资源共享[2]、车辆资源共享[3]、国铁与城市轨道交通的资源共享[3],以及应急状态下的资源调配问题研究[4]。乘务资源共享方面,已有学者提出通过乘务员共享以均衡不同线路间的工作量,但主要集中在优缺点的分析及编制思路的探讨[5],缺少关于具体排班计划优化方法的深入研究。
本文综合考虑乘务员和乘务基地共享条件下的乘务排班计划问题。乘务员共享可以降低不同线路间值乘任务工作量的不均衡性,提高乘务员利用效率。乘务基地共享可以提供更多的出退勤地点选择,满足乘务员就近出退勤的个性化需求,显著节省乘务员出退勤的通勤时间。
传统乘务排班优化问题的研究方法分为基于班次的集合覆盖模型优化[6]和基于乘务区段的网络流问题优化[7]。后者可准确表示一些约束不太复杂的问题,但当问题规模较大时,其模型复杂程度通常远超集合覆盖模型[8]。针对较大规模的乘务排班优化问题,除启发式方法外,主要采用集合覆盖模型结合列生法求解以避免生成规模庞大的可行班次集合。其中,列生成法的关键点在于定价子问题的求解和整数解的获得[8]。文献[9]构建了基于连续值乘区段的多层时空网络图以表示班次可行性约束,之后通过生成网络图集合表示所有可行班次,从而将定价子问题转化为最短路问题。相较于传统乘务排班问题,乘务资源共享需要考虑跨线接续、鲁棒性优化及不同出退勤地点班次比例的控制,且问题规模较大,难以用网络流方法求解。对此,本文在文献[9]提出的网络图模型基础上针对乘务资源共享需求进行调整,改造定价子问题的求解,并采用Gurobi求解整数规划问题的整数解。
1 乘务资源共享分析
乘务资源共享对排班问题的影响可以分为执行和编制两个方面。在执行层面,为实现跨线值乘应将换乘站设置为轮乘站,并需要乘务员具备不同线路列车的驾驶资质。考虑乘务员就近出退勤的需要,应将其按照偏好的乘务基地进行划分,分组独立进行轮班。具体到编制层面,乘务资源共享下的乘务排班问题相较于传统排班问题主要有以下难点。
(1)乘务区段的跨线接续。乘务员仅本线值乘时,地铁排班问题中乘务区段接续关系有3 种:一是乘务员连续值乘同一列车的相邻乘务区段,称为连续值乘接续;其余两种为不同列车乘务区段的接续,根据乘务员在轮乘站进行休息或就餐分为间休接续和就餐接续。乘务区段跨线接续仅包含间休接续和就餐接续,且只发生在换乘站,需要在原接续时间的基础上增加走行时间,并考虑额外的冗余时间以增强鲁棒性。
(2)出退勤比例约束。班次的出退勤地点类型是指班次开始和结束时所在的乘务基地位置,需根据不同出退勤地点偏好的乘务员数量比例,控制不同出退勤地点类型班次的比例。
(3)鲁棒性。乘务员仅本线值乘时乘务计划受扰动影响较小,乘务资源共享后扰动可能使跨线接续无法进行,故乘务计划需要更强的鲁棒性。
(4)问题规模增大。多线间乘务资源共享会增加问题求解规模。
2 模型构建
2.1 优化目标
排班问题研究主要以排班计划效率优化为主[8]。对于鲁棒性的优化考虑增加冗余时间[10],例如提高最小接续时间、减小最大工作时间等,或通过减少便乘以降低延误传播[7]。其中,便乘是指乘务员搭乘其他乘务员值乘的列车转移到其他轮乘站接续所承担乘务区段的行为。由于最小接续时间和最大工作时间是模型参数,本文以班次数为主要优化目标,以总便乘时间为次要目标进行鲁棒性优化。目标函数为
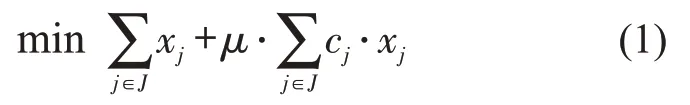
式中:J为可行班次集合;xj为决策变量,当班次j为最终排班计划中的班次时为1,否则为0;μ为鲁棒性优化目标系数;cj为班次j的便乘时间。为便于处理定价子问题,将目标中的cj改为班次j的在车时间c′j(包含便乘时间)。由于总车次任务时间为定值,对总在车时间的优化等价于对总便乘时间的优化。这种转化主要考虑定价子问题求解中是否属于便乘难以界定,而在车时间可以由班次包含的乘务区段时长进行表示。
为优先班次数,需使总班次数远大于总在车时间。可推得μ需满足
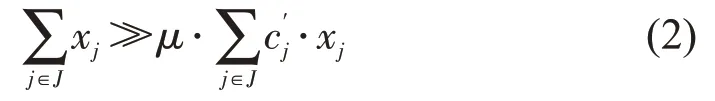
2.2 相关约束
排班约束分为横向约束(班次内可行性约束)和纵向约束(班次间约束)。其中,横向约束主要包含8条,较为复杂,本文设计网络图进行表示,在2.3节介绍。
纵向约束包含乘务区段的全覆盖约束和出退勤比例约束。其中,全覆盖约束保证每个乘务区段均有班次覆盖,即
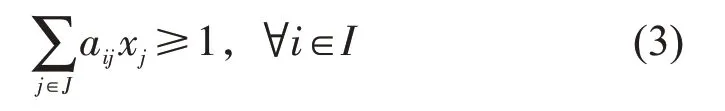
式中:I为乘务区段集合;aij为0-1 变量,当班次j包含乘务区段i时为1,否则为0。
出退勤比例约束保证每种出退勤地点类型班次在最终排班计划中的比例,即
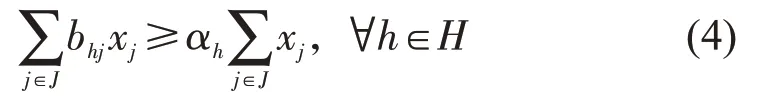
式中:H为出退勤地点类型集合;bhj为班次j是否属于出退勤地点类型h,属于为1,否则为0;αh为出退勤地点类型h所占的比例。
2.3 网络图模型
参考文献[9]提出的时空网络图模型的构建思路,用单层和双层网络图表示无就餐和包含就餐班次的所有可行性约束,通过网络图生成算法考虑不同班次类型和就餐情况分别生成网络图以尽可能表示所有可行班次。以图1所示双层网络图模型为例介绍网络图的构成。枚举所有仅通过连续值乘接续的连续值乘区段,用任务开始和结束点表示连续值乘区段的开始和结束事件,并用任务弧连接对应同一连续值乘区段的任务开始和结束点;用源点和汇点表示班次的开始和结束,并用源点弧连接源点与就餐前层的所有任务开始点,用汇点弧连接就餐后层的所有任务结束点与汇点。为解决出退勤比例约束,在源点弧和汇点弧中间额外插入对应每个轮乘站地点的二级源点和二级汇点,并在其提出的网络图生成算法基础上通过改变一级源点(汇点)与二级源点(汇点)之间的连接将网络图集合分割为对应不同出退勤地点类型的网络图集合,每个网络图集合都只包含对应出退勤地点类型的班次,网络图生成算法如图2所示。除采用间休弧和就餐弧表示间休和就餐接续活动,本文还增加了跨线间休弧和跨线就餐弧以表示跨线接续。
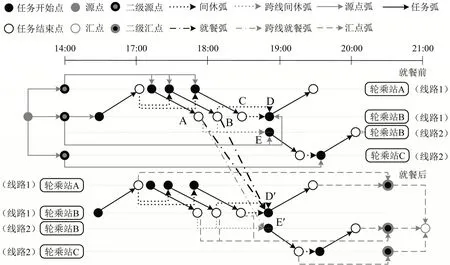
图1 双层网络图模型示意图Fig.1 Diagram of double-layer network
结合网络图对8条横向约束的表示,网络图构建规则如下。
(1)最大连续驾驶时间约束。连续值乘接续不能超过最大连续驾驶时间,枚举所有满足最大连续驾驶时间约束的连续值乘区段作为网络图最小任务单元。
(2)最小和最大接续时间约束。就餐和间休接续应满足各自的最大和最小接续时间,对应到网络图中,规定间休弧和就餐弧只连接满足接续时间约束的任务结束点和开始点,如图1中A、B、C 与D、D′之间的接续。
(3)跨线接续约束。跨线接续需在原最小和最大接续时间基础上增加走行和冗余时间,且只发生在换乘站。在网络图中跨线间休和就餐接续用跨线间休弧和跨线就餐弧表示,只连接换乘站中满足相关时间约束的任务结束点和开始点,例如图1中A、B、C与E、E′之间的接续。
(4)空间接续约束。接续乘务区段的开始地点与被接续乘务区段的结束地点相同,对应到网络图中表现为间休弧、就餐弧、跨线间休弧和跨线就餐弧都只连接同一轮乘站的结束点和开始点。
(5)就餐时段约束。就餐需在给定就餐时段内,故就餐弧和跨线就餐弧仅存在于就餐时段内,例如图1中17:00-19:00时段。
(6)强制就餐约束。包含就餐时段的班次需安排就餐,故采用分层结构的网络图,例如图1包含就餐前和就餐后两层相同的网络图。源点、二级源点和源点弧只连接就餐前层,汇点、二级汇点和汇点弧只连接就餐后层。两层之间仅通过就餐弧和跨线就餐弧连接,因此任何一条从源点到汇点的路径都会经过一条就餐弧或跨线就餐弧。对于不包含就餐的班次则通过单层网络图进行表示,其结构与双层网络图类似,仅包含一层,且不考虑就餐和跨线就餐弧。
(7)最大工作时间约束。每种班次类型有各自的最大工作时间,故将网络图的时间跨度设为对应班次类型的最大工作时间。
(8)工作时间范围约束。每种类型班次需在对应班次类型的时间范围内,因此在网络图生成过程中根据不同班次类型,在其时间范围内分别生成网络图来表示,网络图生成算法如图2所示。
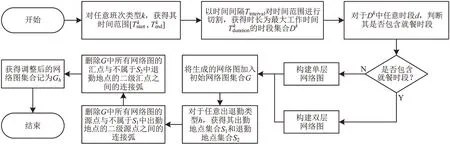
图2 网络图生成算法流程Fig.2 Flow chart of network generation algorithm
单层网络图结构类似,但只包含一层,且无就餐与跨线就餐弧。
3 求解算法
在网络图模型的基础上,将定价子问题转化为若干个网络图集合的最短路问题,采用列生成法求解。列生成法将问题划分为主问题(Master Problem,MP)和定价子问题(Pricing Problem,PP),循环迭代求解,总体算法流程如图3所示。阶段1为准备阶段,构建对应的网络图集合和初始可行班次,网络图生成算法如图2所示;阶段2为传统的列生成迭代优化阶段;阶段3为整数解获取阶段。
阶段2 中定价子问题的求解是列生成法的关键,根据主问题确定定价子问题的表达式。标准排班计划主问题可表示为
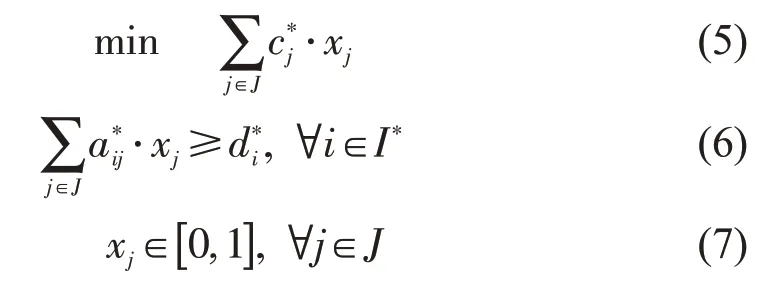
式中:I*=I⋃H,包含全覆盖约束和出退勤比例约束;c*j为标准化后目标的价值系数,根据式(1)可以推得c*j =1+μ·c′j;a*ij和d*i为标准化后约束的消耗系数和资源限制系数,根据式(3)和式(4),可得
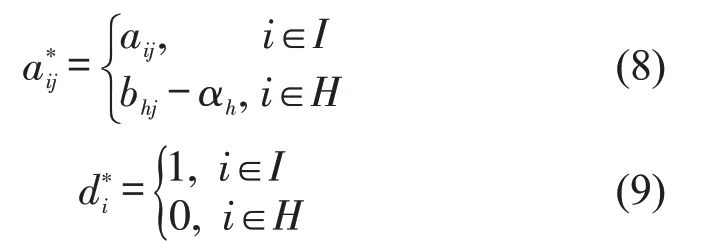
代入c*j和a*ij可以得到定价子问题为
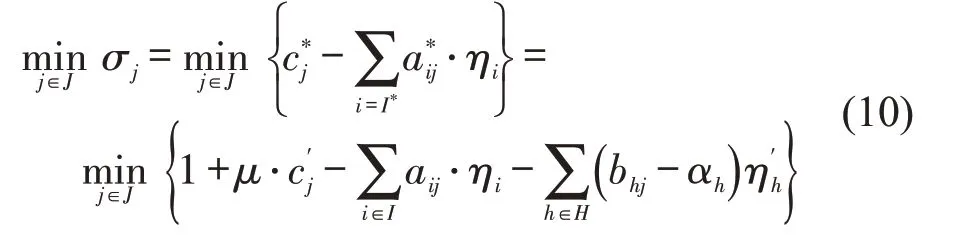
式中:σj为班次j的检验数;ηi为第i个乘务区段全覆盖约束的影子价格;η′h为出退勤地点类型h出退勤比例约束的影子价格;c′j为班次j的在车时间,可转化为每个乘务区段在车时间ti之和。据此,式(10)可转化为
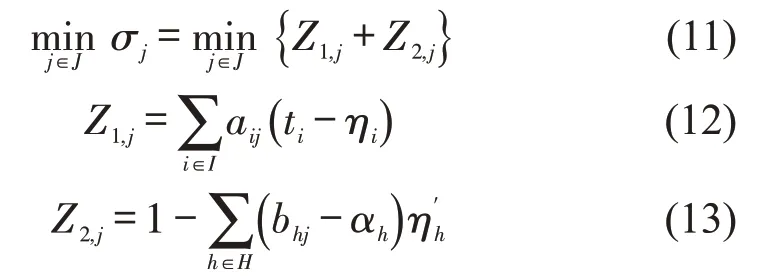
式中:Z1,j完全取决于班次j覆盖的乘务区段;Z2,j取决于班次j的出退勤地点类型。因此,只要将网络图中的任务弧弧长设置为

式中:λl为任务弧l的弧长;Il为任务弧l对应的连续值乘区段所包含的乘务区段集合。即可通过最短路算法获得每个网络图中Z1,j最小的班次。
Z2,j完全取决于班次j的出退勤地点类型,只需获得每种出退勤地点类型对应的网络图集合Gh的最短路,其中必然有一条为定价子问题搜索的最优解。具体到算法中表现为在阶段2 列生成迭代中,将所有出退勤地点类型对应的网络图集合Gh的最短路都加入主问题的班次集合P中。
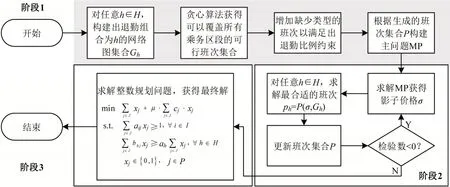
图3 求解算法流程Fig.3 Flow chart of solution method
4 案例分析
4.1 案例背景
以北京市2条地铁线路为背景进行案例分析,线路信息如表1所示。轮乘站A 为两条线路的换乘站,班次的出退勤地点包括A、B两个轮乘站及车辆段。假设乘务员对轮乘站A、B有各自偏好,但均可以接受在车辆段出退勤。根据出退勤地点可将班次划分为4 种类型,如表2所示。偏好轮乘站A的乘务员可接受类型1 和3 的班次,偏好轮乘站B的可接受类型2 和3 的班次,类型4 班次分别在轮乘站A、B出退勤,其数量比例得到控制。
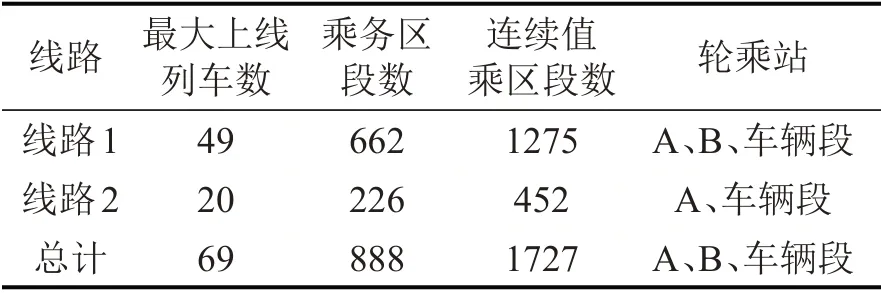
表1 线路信息Table 1 Line related parameters
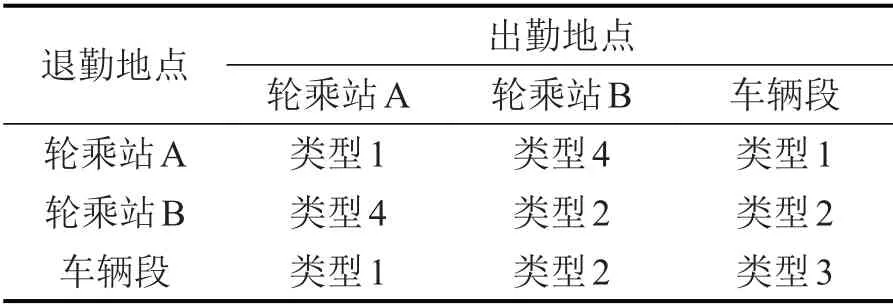
表2 班次出退勤地点分类Table 2 Shift classification based on starting and ending locations
4.2 优化结果分析
以分线单独优化排班计划作为对照组,实验组为基于乘务资源共享的5 组方案,如表3所示。表中最后3列为方案的出退勤比例约束参数。例如,方案3 要求类型1 加类型3,以及类型2 加类型3 的班次比例均不小于45%,类型4的班次比例不大于10%,分别对应对轮乘站A、B有偏好及对出退勤地点无偏好的乘务员比例。对照组在构建网络图时不考虑跨线就餐和间休弧,其余模型算法与方案1相同。

表3 案例方案设计Table 3 Set of cases
算法阶段3中采用Groubi求解整数规划问题,最大求解时间设为4 h。案例结果如表4所示,其中,工作效率为有效驾驶时间除以总工作时间。对比对照组与实验组的结果可知:乘务资源共享之后可节省3个班次,提高工作效率0.33%~1.77%,说明乘务资源共享可缓解值乘任务时空上的不均衡性进而提高乘务员利用率;方案5与方案1相比,可减少39.05%的便乘数量,证明鲁棒性优化可以有效减少便乘,降低延误传播风险,但多线路协同优化及对出退勤地点的限定产生一定的便乘需求,因此优化结果中存在一定比例的便乘,增加了不同轮乘站间司机转移的需要和乘务员便乘时跨线值乘的需要;方案3~方案5 的结果表明,乘务基地和乘务员共享可更好地满足乘务员对出勤地点的个性化需求,在班次数小幅减小的前提下仍能达到不同出退勤地点类型班次的比例。例如,对不同出退勤地点类型班次数进行推算,方案5 比方案1 每天可多满足27 位乘务员的出退勤地点偏好需求,显著提高了乘务员的通勤出行便捷性。
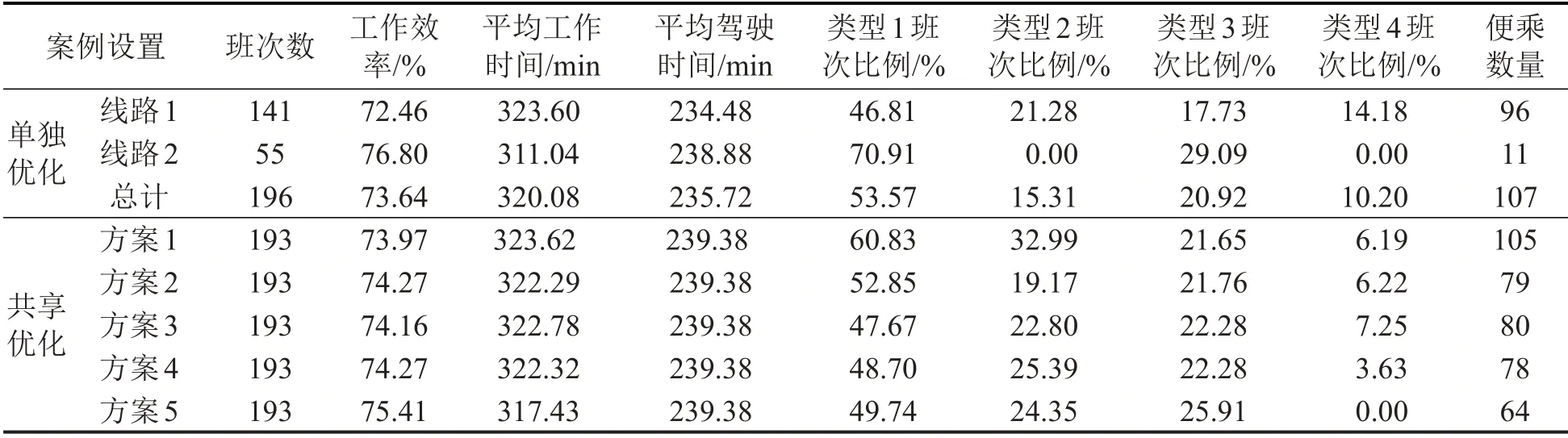
表4 案例结果分析Table 4 Analysis on results from case studies
5 结论
本文对基于地铁乘务资源共享的排班计划优化问题进行了研究,考虑乘务基地和乘务员共享对排班问题的影响,设计网络图模型和优化方法,并通过实际线路开展了案例研究。案例结果表明:考虑乘务资源共享可提高不同线路间乘务资源的利用效率,增加排班效率并小幅减少班次数;在给定不同出退勤地点类型班次比例的情况下,可更好地满足乘务员对出退勤地点的偏好,提高乘务员通勤出行的便捷性。
