带柔性休息时间的多技能呼叫中心班次设计

戴 韬，李军祥

DAI Tao1,LI Junxiang2

1.东华大学 旭日工商管理学院，上海200051

2.上海理工大学 管理学院，上海200093

1.Glorious Sun School of Management,Donghua University,Shanghai 200051,China

2.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China

1 引言

1.1 背景

呼叫中心（Call Center）作为一种成熟运营模式已广泛应用于各社会各行业中，成为各自保持客户联系的关键渠道与制胜法宝。多技能指呼叫中心能提供超过一种的服务，其坐席人员也被培训有一种或多种服务的技能。多技能呼叫中心是呼叫中心发展的必然形态。

呼叫中心是典型的技术、劳动力双重密集型产业，其运营过程不仅仅依靠计算机、通讯等软硬件的支持，更需要大量的坐席人员（Agent）参与服务。因此，呼叫中心运营的60%～70%是坐席代表的人工成本，合理的人员排班是实现高效率的呼叫中心运营管理，降低整体运营成本，保证客户服务质量和服务水平，提高呼叫中心生产力的最重要一环[1]。

1.2 班次设计的内涵

广义的人员排班一般分为3 个步骤[2]：

（1）根据历史数据预测未来一段时间内每个时间段（以15 分钟或半个小时为单位）的顾客来电量；

（2）按照预测的每个时间段的来电量，在满足服务水平的前提下，确定各技能的人员数量；

（3）将坐席人员安排到各备选班次中，不但要满足第（2）步的人力需求，而且还要考虑到坐席人员的个性化需求。

其中班次设计（Shift Design）是步骤（3）中最重要的基础性工作，是人力需求预测与计算与后续人员排班的桥梁。明显地，一套合理的班次应该很好的符合话务量变化规律，如果班次设计不合理，再好的人力需求计算也变得没有价值，后续的人员排班步骤也没有了意义。

在班次设计中，每个班次的持续时间都是相同且已知的，该持续时间受工人合同、法律法规等限制，如8 小时工作制。这样，班次设计的主要内容就是[3]：

（1）确定总的班次数，以及各班次的开始时间与结束时间；

（2）确定每个班次的休息时间，保证所有上班人员均能享受到必须的休息；

（3）确定每个班次需要的上班人数，将以时间段（period）为单位的人力需求转换为以班次（shift）为单位的工作量。

2 文献综述

在班次的设计中，主要的困难是班次的不连续性（因为有休息的时间窗）。若假设所有的班次都是连续的（从开始一直工作到结束），那么班次矩阵（矩阵的行是时间段，列是备选班次数）是完全幺模矩阵（totally unimodular）。在该假设下，文献[4]研究了设计最优化班次的方法，并得到了最优解；文献[5]提出了单技能环境下完整的班次设计模型；文献[3，6]提出了多技能环境下班次总体数目及起始时间的确定模型。

当允许班次中断后，班次矩阵就不再是幺模的，该问题就变得复杂得多，文献[7]已经证明该问题是一个完全NP 难题。对于该难题的代表性研究分别从建模与算法两方面展开。在建模方面，文献[8]提出不要用覆盖模型来研究这个问题。文献[9]和文献[10]将变量分为两组，一组表示班次的起始时间，另一组表示班次的中断时间，这样的变量设置方法就避免了使用覆盖模型来求解。在算法方面，文献[11]做了这方面的工作，他将班次设计分为两个步骤：第一步假设班次是不中断的，使用网络流模型得到最优解；第二步通过启发式的方法往第一步的结果中加入中断时间，最后得到可行解。文献[12]也做了这方面的工作，在确定班次矩阵的时候就采用了一些启发式的方法使得这个矩阵的规模不要过于庞大。另外由于覆盖问题的规模比较大，通常是几百行，上千列[7]，很难以全局搜索的方法来找最优解，而应该使用模拟退火、遗传算法等局部搜索的方法，文献[13]提出了基于邻域搜索的班次设计算法。

对于班次设计的研究不仅仅局限于呼叫中心领域，文献[14]综述了人员排班领域的文献；文献[15]研究了多工作点的班次设计问题；文献[16]研究了医疗服务行业的班次设计问题；文献[17]研究了运输行业的班次设计问题。

综上，在呼叫中心领域，虽然已分别有论文研究了多技能连续性班次的设计方法以及单技能中断性班次的模型与算法，但结合两者，即考虑休息时间的多技能班次设计却鲜见讨论。在多技能的环境中，班次的设计将会变得更加复杂，因为某技能组人员的增减不单单影响本技能组的人员供给，还会交叉影响与其相关的其他技能组的人员供给[1]。

3 模型与算法设计

3.1 基本思路

3.2 连续性班次设计模型

为了得到简化的多技能班次设计模型，借鉴文献[3]提出的“技能稳定”（skill frozen）思路，一个多技能的坐席人员虽然可以接听多种类型的电话，但是在一个时间段里，他仅仅可以根据当时各类电话的空闲情况以及自身的技能列表，选择一种进行服务，并且在这个时间段内，不允许再有变化。“技能稳定”假设可以便于将多技能坐席人员拆分变成单技能的坐席人员，得到简化的连续多技能的班次设计模型（模型1）如下（不考虑休息时间窗）：

模型1多技能连续班次设计模型

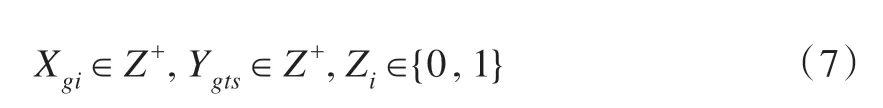
模型1 的目标函数（1）表示排班周期内总的人力成本最低，其中决策变量Xgi表示技能组为g的坐席人员安排到第i个班次上班的人数；Cgi为已知量，表示技能组g的坐席人员上i班次的报酬；约束（2）引入了一个中间变量Ygts，表示技能组g的坐席人员在第t时间段以技能s上班的人数，Ygts与Xgi的关系如约束（2）所示，其中ait=1 表示时间段t是第i班次的工作时间段，等于0 则反之；约束（3）确保了一个多技能坐席人员在一个时间段内只能“扮演”某中特定的单技能坐席人员的角色，并且他所“扮演”的角色是受其技能列表所限的，bgs=1 表示技能组g拥有技能s，等于0 则表示没有；约束（4）中的表示确定的第t时间段s类型电话的人力需求（通过人力需求计算获得，属于班次设计的已知条件），该约束确保了各类型的人力需求都能够被满足；约束（5）中的常量ζ是一个大正整数，该约束保证只要被指派了坐席人员的班次被标记为“使用过”班次；约束（6）表示总的“使用”班次不能超过限定值M；约束（7）则确保变量Xgi和Ygts是个非负整数，而Zi为0-1变量。

文献[3]已讨论过如何利用该模型，通过逐步放松参数M 的限制，得到连续性班次。本文借鉴其方法，不详细展开讨论。

3.3 空闲劳动力计算

模型1 得到了多技能环境下最合适的M个班次，但这些班次都是连续工作的，在实际应用中无法接受。考虑如何在连续工作的班次中，加入休息时间。

首先，利用已知的M个连续班次，将把排班周期内的以时间段为单位的人力需求转化为以班次为单位的人力需求：

模型2人力需求转换模型（时间段→班次）

模型2 是模型1 在日期维度上的改进和扩展，所有变量与约束的含义均与模型1 相同，除了用确定的班次集M取代了模型1 中的备选班次集I，另外也去掉了原模型中班次总量限制。模型2 虽然时间维度上的规模变大了，但班次维度问题规模的缩减和班次总数约束的去除，仍保证了该模型能够比较容易求解。

模型2 的主要功能是得到在连续工作的班次下，空闲的工作能力，有空闲的工作能力存在就说明存在潜在的休息可能性。模型2 中用Sjts表示第j天第t时刻以技能s工作的坐席人员人数，而变量ΔOjts表示在第j天第t时刻以技能s工作的空闲的坐席人员人数。

通过模型2 的转换后，休息时间窗的加入在本质上就变成了一个分配问题（Assignment Problem），其基本思路是以ΔOjts为供给，以坐席休息时间为需求，进行人力分配，直到给所有的坐席人员都安排了休息时间为止。

3.4 休息时间加入

为了表述方便，设定坐席的休息规则如下：每个班次需3 个休息时间，其中第一个休息时间在班次开始后的2～3.5 h，持续15 min，记为b1；第二个休息时间是长休息时间（用餐等），在班次开始后的4～5 h，持续30 min，标记为b2；第三个休息时间在班次开始后第6～7.5 h，持续15 min，标记为b3（注：该休息规则仅仅是较有代表性的一种，不同呼叫中心可根据情况进行调整）。

由模型2 已经得到了每时刻多余的人力ΔOjts，这里多余的人力是按照技能类型来分类的，根据3.3 节的思路，可以得到多技能的环境下多余人力与休息时间的分配模型：

模型3多技能环境下多余人力与休息时间的分配模型

模型3 中没有了日期维度的变量J，因为模型3 是在模型1 得到的连续性班次基础上，根据每天的话务量变化动态地加入休息时间。若排班周期共J天，需要将模型3 执行J次。

目标函数式（14）中的变量Zt是一指标性的0-1 变量，若t时刻需要休息的人数大于空闲的人数（即无法保证所有该休息的坐席得到休息）Zt=1，反之为0；约束（15）是确保所有上班的坐席人员能在班次开始2～3.5 h内安排到休息b1，决策变量表示技能组为g在m班次上班的坐席在bm+8 时刻开始b1休息的人数，其中bm是班次m的开始时间，已通过模型1 计算得到，变量Xgm是技能组g在m班次上班的总人数，已通过模型2 得到；同理，约束（16）确保在班次开始4～5 h 内安排到b2休息；约束（17）是确保所有上班的坐席人员能在班次开始6～7.5 h 内安排到b3休息；约束（18）引入了一个新的变量Y′gmts，表示g技能组在m班次以s技能工作的坐席在t时刻休息的人数，等于3 类休息的人数汇总；约束（19）限制了空闲的人数至少不能超过上班的人数，其中上班人数Ygmts已经由模型2 计算获得；约束（20）和（21）共同作用，确保在每个时刻t，若休息人数大于了空闲的人数，标记Zt为1。

3.5 算法设计

本文涉及到3 个基本模型，每个基本模型均属于典型的线性整数规划问题，可以直接应用已有成熟的算法或软件进行求解，这里讨论的算法是如何综合利用3 个模型得到最终带有休息时间的班次。

从分析模型3 入手，其目标函数的下限是0（表示所有的时刻t，空闲人数均大于计划休息的人数），即可以在不影响服务水平下，所有坐席均得到应有的休息，这也是最终班次设计的要求。目标函数值>0，说明至少存在一个时刻待休息的人数大于空闲人数，即在给定的连续性班次和上班人数下，无法保证每人都能满足休息需求。因此，只有通过增加上班人数来保证所有人均得到休息，增加的方法是：

（1）找出Zt值为1 的所有时刻t；

（2）检查变量Zts=1，找到具体是哪一技能坐席的人员不足；

（3）对Zts=1 的时刻t，构造“虚拟”人力需求即在原实际坐席人力需求rts+1，再重新进行模型2 的计算，迭代，直到模型3 的目标函数=0 为止。

需要注意，模型3 仅仅得到是1 天的班次安排，对于周期为J天的排班过程，需要将模型3 迭代J个过程。综上，得到最终的算法示意如图1 所示。

由图1 可知，本文的班次设计算法是两阶段的。第一阶段得到连续性的班次，第二阶段在此基础上加入休息时间，最终得到的班次使得每个班次中上班的人员均能保证得到该有的休息。不仅于此，由于模型3 是每天独立运行的，在保证总班次数不增加的前提下（管理的方便），每个班次的休息时间能根据当天话务量的变化动态调整。另外，除了班次表之外，可以得到以班次为单位的人力需求，相比以时刻为单位的人力需求，更有助于后续的人员排班。

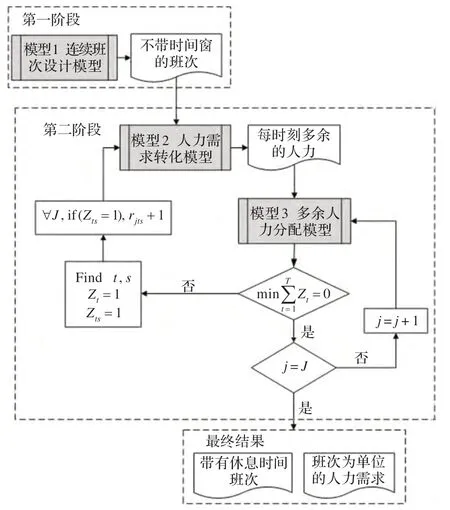
图1 两阶段班次设计算法示意图

4 算例实验

4.1 算例假设

本文的算例跟文献[3]中的一致，其结构如图2所示。

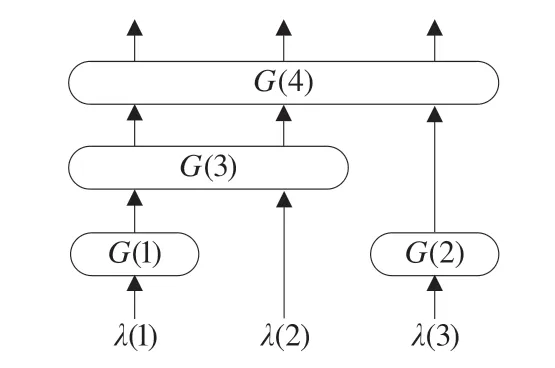
图2 某呼叫中心结构图

该呼叫中心一共处理3 种类型的电话(S=3)，共有4 个技能组的坐席人员(G=4)，每15 min 为一个时间段(T=96)，时间段内电话的到达率、服务率甚至是多技能坐席人员处理的电话类型都是不变的，设定班次只能在半点或者整点的时候开始，备选的班次总共有48 个(I=48)，班次的持续时间都是8 h。

由图2，可以得知各技能组拥有的技能，组成技能矩阵：矩阵中的元素bgs=1 表示技能组g拥有技能s。

假设处理同种电话，不同技能组的服务率是相同的，以时刻为单位的3 类电话的人力需求已知；不同技能组上不同的班次给予不同的酬劳，具体的酬劳已知。

4.2 算例求解

将4.1 节中的已知条件代入到模型1 中进行求解，通过逐步限定班次总数M，得到最优连续性班次如表1。文献[3]已详述过程，不再赘述。

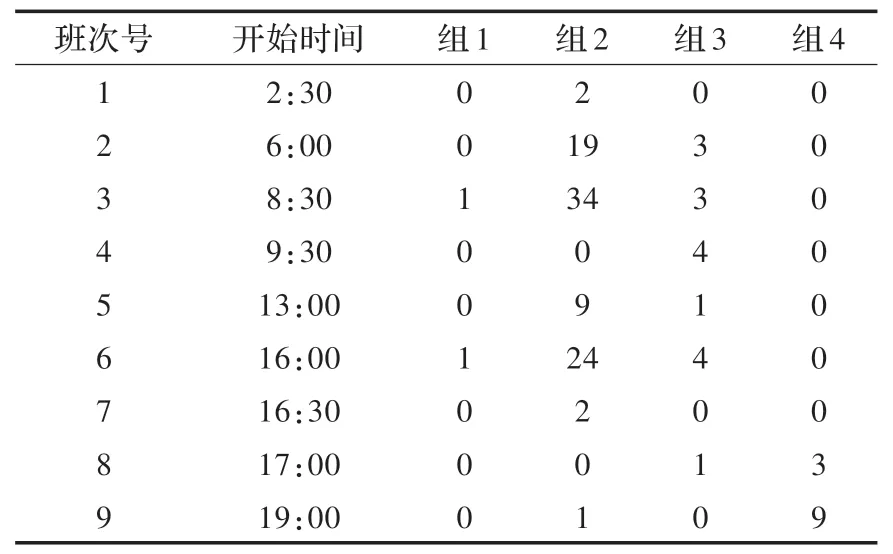
表1 连续性班次及需求人数

根据图1所示算法，得到连续性的班次后，将其作为已知代入到模型2 得到各时刻下的空闲人力。以类型3电话为例，得到某天电话3 的人力需求与供给如图3。

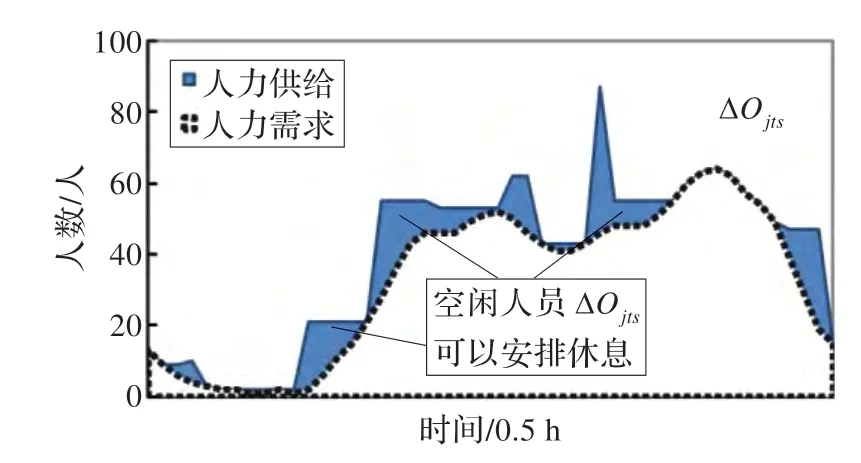
图3 某天电话3 人力需求与供给

模型3 的迭代过程即是以图3 中阴影表示的空闲人力为供给，保证表1 内9 个班次的坐席人员均能按要求享受到休息。根据本文设计的算法，可得到最终带有休息时间的班次，以表1 中的班次3 为例，最后的班次安排如表2。

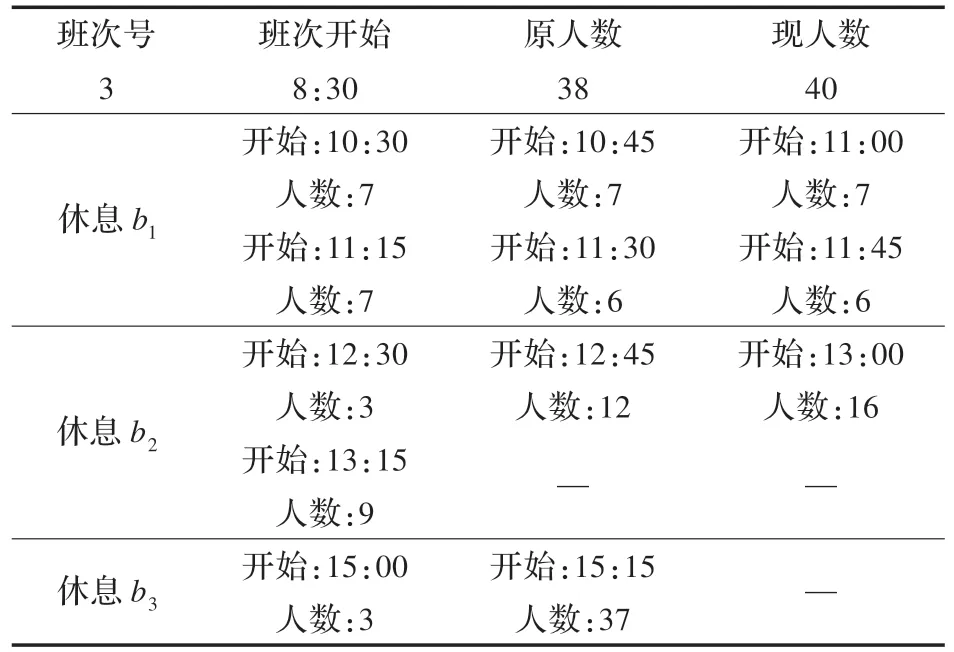
表2 带休息的班次表（班次3）

其余各班次也得到类似的结果。通过算例也发现了两个不甚满意的地方：

（1）由于空闲人力紧张，休息b1被拆分成了6 个时间段进行休息，不利于现场管理。

（2）为了有更多的空闲人力保证足够的休息，班次3由原来的上班38 人增长为40 人。分步优化可能偏离了全局最优解。

5 结论

班次设计是呼叫中心人员排班的基础性工作，尤其在多技能的环境下，是完全NP-hard 问题。本文根据分步优化的思想，设计了相应模型与两阶段算法，先计算连续性班次，再通过改进的指派模型将休息时间安排到班次中，得到可行解，并通过班次的设计，将原以时刻为单位的人力需求转化为以班次（跨越N个时刻，一般N≥30）为单位的人力需求，使得后续的人员指派步骤规模缩小N倍，便于后续指派模型的求解。

由于算法是分步进行的，每次仅得到局部的最优，特别是在连续性班次下人员供给曲线与需求曲线切合得较好的区域，为了能得到足够的空余人力保证休息时间，需要不断增加额外的上班人数，不单因为迭代次数过多影响了求解速度，与全局最优解的差距也在加大，因此算法的速度及其收敛性是本文后续研究方向。

[1] Gans N，Koole G，Mandelbaum A.Telephone call centers：tutorial，review，and research prospects[J].Manufacturing &Service Operations Management，2003，5（2）：79-141.

[2] Ernst A T，Jiang H，Krishnamoorthy M，et al.Staあscheduling and rostering：A review of applications，methods and models[J].European Journal of Operational Research，2004，153（1）：3-27.

[3] Dai T，Huo J.A research on shift scheduling in multi-skill call center[C]//Proceeding of 2008 IEEE International Conference on Service Operations and Logistics，and Informatics，2008：655-658.

[4] Nemhauser G L，Wolsey L A.Integer and combinatorial optimization[M].[S.l.]：Wiley InterScience，1988.

[5] Brusco M J，Jacobs L W.Starting-time decisions in labor tour scheduling：An experimental analysis and case study[J].European Journal of Operational Research，2001，131：459-475.

[6] Bhulai S，Koole G，Pot A.Simple methods for shift scheduling in Multiskill call centers[J].Manufacturing & Service Operations Management，2008，10（3）：411-420.

[7] Caprara A，Monaci M，Toth P.Models and algorithms for a staff scheduling problem[J].Mathematic Programming：Series B，2003，98：445-476.

[8] Thompson G M.Improved implicit optimal modeling of the labor shift scheduling problem[J].Management Science，1995，41：595-607.

[9] Aykin T.Optimal shift scheduling with multiple break windows[J].Management Science，1996，42：591-602.

[10] Brusco M J，Jacobs L W.Optimal models for meal-break and start-time flexibility in continuous tour scheduling[J].Management Science，2000，46：1630-1641.

[11] Segal M.The operator-scheduling problem：A network-flow approach[J].Operations Research，1974，24：808-823.

[12] Henderson W B，Berry W L.Heuristic methods for telephone operator shift scheduling：an experimental analysis[J].Management Science，1976，22：1372-1380.

[13] Quimper C G，Rousseau L M.A large neighborhood search approach to the multi-activity shift scheduling problem[J].Journal of Heuristics，2010，16（3）：373-392.

[14] den Bergh J V，Belien J，Bruecker P，et al.Personnel scheduling：A literature review[J].European Journal of Operation Research，2013，226：367-385.

[15] Al-Yakoob S M，Sherali H D.A column generation approach for an employee scheduling problem with multiple shifts and work locations[J].Journal of the Operational Research Society，2008，59：34-43.

[16] Brunner J O，Bard J F，Kolisch R.Flexible shift scheduling of physicians[J].Health Care Management Science，2009，37（12）：285-305.

[17] Knust S，Schumacher E.Shift scheduling for tank trucks[J].Omega-International Journal of Management Science，2011，39：513-521.