智能控制策略在燃气锅炉燃烧优化中的应用

杨 凯 薛美盛

（1.中国空空导弹研究院；2.中国科学技术大学信息科学技术学院）

在燃烧控制系统中，空气调节系统的任务是保证进入燃烧系统的燃料充分燃烧，使其达到最高的燃烧效率［1］。由于锅炉燃烧系统具有强耦合、非线性等特点，导致燃烧过程的燃烧效率受诸多因素的影响，其中空燃比就是一个重要指标。 空燃气比直接决定烟气中的氧含量值，而烟气的氧含量值能够反映系统的燃烧效率，因此人们不断寻找空燃比的优化方法，以提高燃烧效率，实现经济燃烧。

燃气锅炉燃烧系统中能反映燃烧状态的参数除了烟气氧含量之外，还有一个重要参数就是炉膛温度［2，3］。对炉膛温度起决定性的因素是煤气燃烧后它的产物所能达到的温度，确保炉膛温度始终处在最高值的附近，实质上就是在实现经济燃烧。 笔者针对某现场燃气锅炉控制系统，构建了BP神经网络用于描述影响炉膛温度各因素之间的关系，运用粒子群优化算法和模糊控制算法设计并实现了一套可用于锅炉燃烧系统的智能控制策略， 成功改造了原有的燃烧控制系统，在现场取得了良好的应用效果。

1 构建燃烧系统神经网络模型

由于燃烧系统具有非线性、 强耦合的特点，若采用建立精确数学模型的方式来模拟复杂多变的燃烧过程， 将导致构建出的模型异常复杂，难以应用［4，5］。然而人工神经网络在非线性拟合方面有着良好的性能，能够满足对该过程的建模需求，故采用BP神经网络对燃烧过程建模，然后利用构建出的模型设计相应的控制器［6］。

构建神经网络模型， 首先要选取合适的数据。 通过采集某燃烧系统的输入输出数据，经过对数据的反复筛选，选出能够反映燃烧系统运行过程中的一些关键参数，并进行预处理。 经过预处理后共选出5 000组样本数据，其中每组数据包含炉膛温度、上层空气阀开度、上层煤气阀开度、下层空气阀开度、下层煤气阀开度、煤气和空气总管流量，共7个变量。 图1是均值滤波处理后的炉膛温度数据。

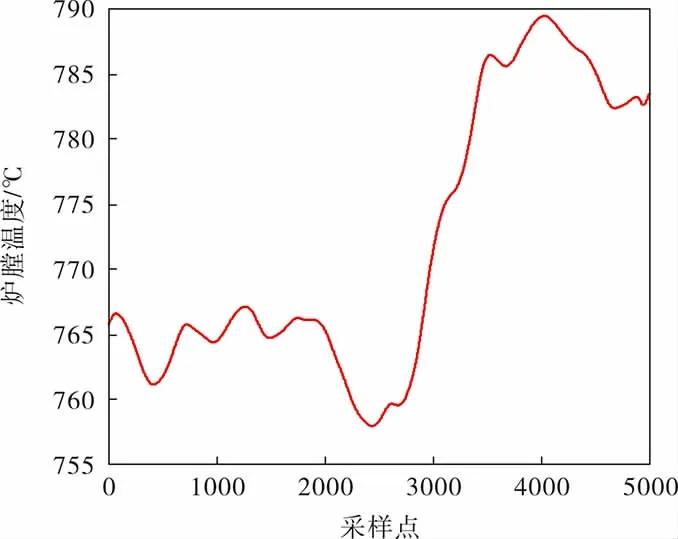
图1 均值滤波处理后的炉膛温度曲线

构建BP神经网络模型用于描述影响炉膛温度各变量之间的关系。 数据划分采用随机抽取的方式，抽取样本数据的90%用于模型训练，余下的10%用来验证模型的实际效果， 模型的评价方式以准确度为评估标准，用MSE（均方误差）进行度量。 考虑到采样数据中有些变量存在相关性，因此对部分变量进行处理，即把同层的空气阀和煤气阀开度的比值作为一个变量， 减少变量个数，给模型构建带来方便，并对各变量进行归一化处理。 最终选取上层空气和煤气阀比值、下层空气和煤气阀比值、煤气总管流量、空气总管流量这4个变量作为网络的输入变量，炉膛温度作为网络的输出变量，构建一个4输入1输出的空燃比神经网络模型。

由于网络的输入变量不多，考虑采用单隐含层结构，通过线下试验得知隐含层节点数为9时，均方误差最小。 在MATLAB环境下进行网络模型的训练，取迭代次数200、学习速率0.03、目标误差0.000 02，学习算法采用L-M算法，最终网络的预测结果和预测误差如图2、3所示。

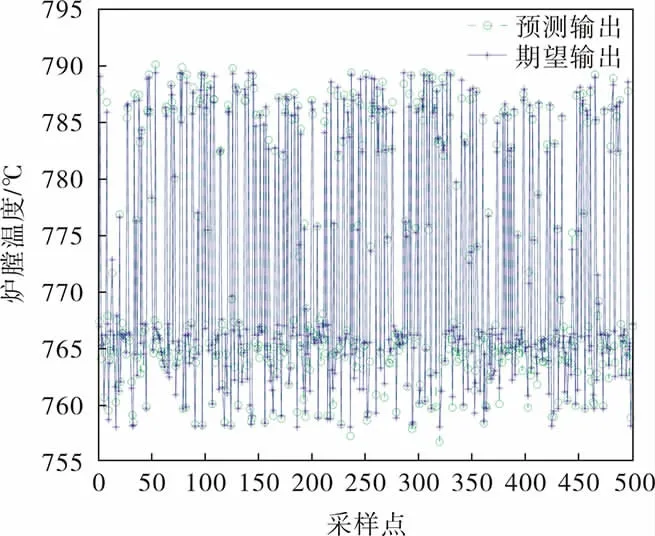
图2 BP神经网络预测结果

图3 BP神经网络预测误差

从图3可以看出，预测误差大都集中在［-3，3］之间，只有极少部分不在该范围内，评价标准MSE为0.68。因此利用神经网络构建出的空燃比模型，其预测结果是令人满意的。

2 粒子群算法优化空燃比

通过BP神经网络对炉膛温度等变量进行建模，利用具有全局搜索能力的粒子群优化算法求解模型的最优解，即找出燃烧系统中存在的最佳空燃比，整个求解空燃比的算法流程如图4所示［7，8］。

采用基本粒子群算法进行全局搜索时，只需对算法中的参数进行设置即可。 算法中的优化目标是找到最佳空燃比使得此时炉温最高，可将其变成求解极小值的过程。 因此目标函数选用BP网络中炉温模型输出值的倒数， 并将它作为适应度函数，其取值越小，表明结果越好。在粒子群优化算法的作用下， 得到适应度变化如图5所示。 可以看出，经过29次迭代进化后，目标函数最小值为0.001 251，将其转换为实际的炉膛温度即799.36℃， 得到上层空燃比和下层空燃比分别是为2.15和1.62。

以上完成了BP神经网络建模-粒子群算法优化空燃比的过程，将得到的结果作为上下层的空燃比基准值，应用到自适应模糊控制中，实现对烟气氧含量的控制。

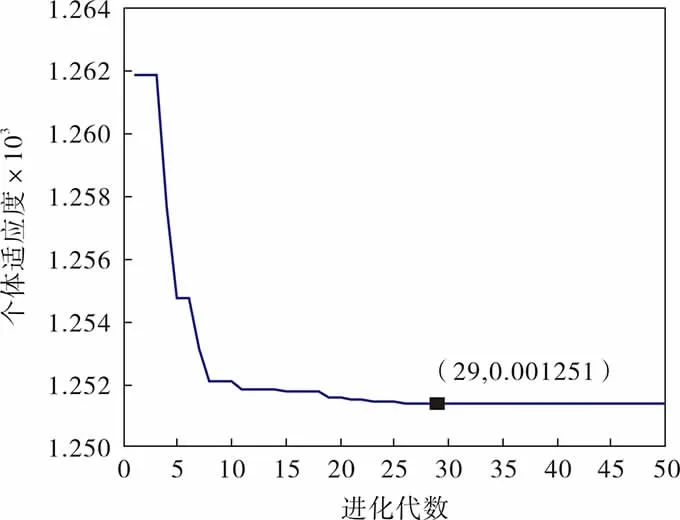
图5 适应度变化曲线

3 设计自适应模糊控制器

对于燃烧系统中烟气氧含量的控制，以氧含量误差e和误差变化率ec为输入变量，以空气调节阀增量u为输出变量， 采用双输入单输出的控制器结构。 为简化模糊推理的计算过程，采用单点模糊法进行模糊化，选择重心法进行精确化计算［9，10］。 输入和输出量均选用三角形隶属度函数，如图6所示。

(5)刊载情报信息机构知识服务研究成果的期刊主要有《图书情报工作》、《情报理论与实践》和《情报杂志》等，为我国知识服务理论的导入和实践经验的推广发挥了重要的作用。广大科技服务工作者应将其作为重点关注对象，了解本领域的发展动向和态势，提高自身的理论水平和实践能力，更好地服务于国家创新创业工作。

图6 e、ec和u的隶属度函数

根据实际工艺工程和操作经验，构建的模糊控制规则见表1。

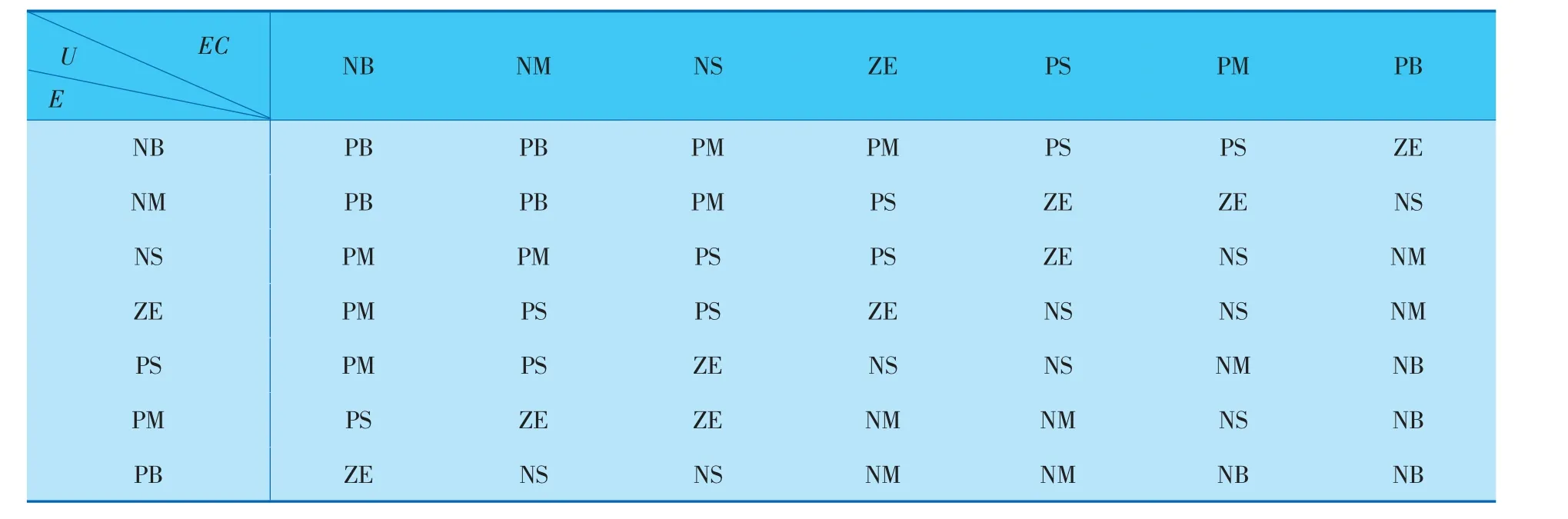
表1 模糊控制规则

a. 如果-2.5≤e＜-1或3＜e≤5，|ec|≥0.35，则Ke=0.4、Kec=2.5、Ku=2；

b. 如果-1≤e＜0或2＜e≤3，|ec|≥0.25， 则Ke=0.6、Kec=3.5、Ku=1.8；

c. 如果1＜e≤2，|ec|≤0.2， 则Ke=0.7、Kec=4.5、Ku=1.4；

d. 如果0＜e≤1，|ec|≤0.1， 则Ke=0.8、Kec=5.5、Ku=1.2；

e. 其他情况， 则量化因子Ke=0.8、Kec=6、Ku=1.7。

4 空燃比优化策略应用

通过前面构建的BP神经网络炉膛温度模型，利用粒子群优化算法求出上下层空气煤气调节阀开度的比值；以此作为空燃比基准值，当每次调整煤气阀开度时，将该开度值乘以对应的空燃比基准值作为此刻的空气调节阀开度；最后根据实际燃烧过程中氧含量设定值和实际值之间的偏差情况，结合自适应模糊控制计算出空气调节阀需要的微调量， 作为最终的空气调节阀开度值。 算法框图如图7所示。

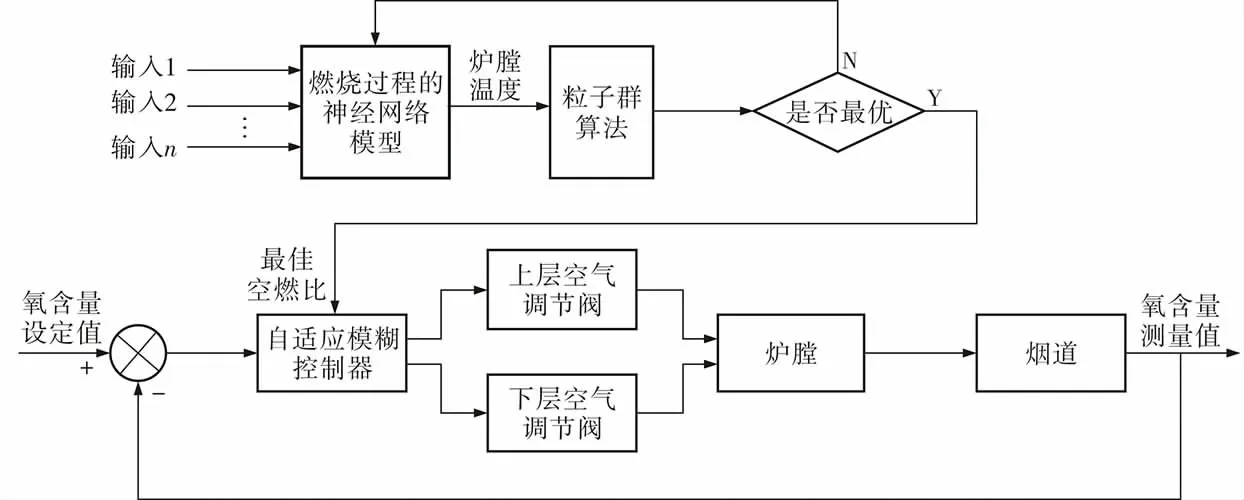
图7 空燃比优化-氧含量控制算法框图

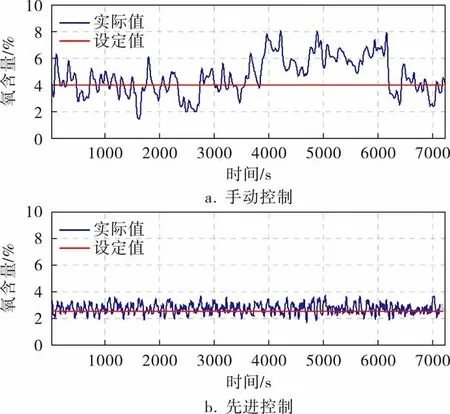
图8 先进控制系统投运前后烟气氧含量对比

5 结束语

为提高某钢铁厂燃气电站锅炉燃烧系统的燃烧效率， 笔者选取燃烧过程的输入输出数据，利用人工神经网络技术， 通过对样本数据的学习，建立了燃烧系统的数学模型，以粒子群算法求解的最佳空燃比为基准，采用自适应模糊控制与神经网络建模相结合的方式，设计了一套智能控制策略，实现了对燃烧系统的空燃比优化。 实际投运结果表明，烟气氧含量回路的控制效果明显改善，波动范围大幅降低，从而提高了燃烧效率。