单容水箱液位随动系统的模糊控制研究

王俊伟 于新海 刘丽秋

（河套学院机电工程系）

由于PID算法的应用比较简单而且性能分析比较容易［1，2］，因此在过程控制领域应用较为成熟。 当系统具有线性特征时PID控制效果较好，但是对于系统的非线性特征，由于没有精确的数学模型，传统PID控制效果较差［3］。

单容水箱液位恒值控制采用PID算法可以满足控制要求， 但是当液位随着时间快速变化时，PID算法的控制精度较差，很难应用于该场合。 单容水箱液位随动系统可以看作是简单的多变量非线性系统，多变量非线性系统的控制在过程控制领域占有很重要的地位［4］。 过程控制领域中大多数是非线性和难以建模的系统，因此研究非线性的自动控制具有重要意义［5，6］。

实现水箱液位控制的方法有人工经验法、闭环反馈PID算法、模糊控制及视觉检测法等。 工程中主要利用闭环反馈PID算法。 视觉检测法与传感器检测法误差较大，应用不太成熟［7］。采用模糊控制技术对随动系统进行控制， 相较于PID算法的优势是可实现非线性控制。 因此，笔者采用模糊控制实现单容水箱液位随动系统的控制。

1 模糊控制原理

模糊控制是以模糊集合、语言变量、语言规则和模糊推理为基础的一种智能控制方法，是模仿人的推理和决策的过程［8］。模糊控制原理如图1所示，将传感器反馈的信号进行模糊化，转换为模糊集合（采用语言变量描述），然后作为模糊规则的输入，经过推理运算之后得到一个模糊集合输出，而控制输出为真值变量，所以需要将模糊规则输出的模糊集合进行解模糊化，最终得到真值的输出。

图1 模糊控制原理框图

2 水箱液位模糊控制系统

建立水箱液位模糊控制系统，首先需要深入了解水箱液位的工艺流程，然后按照模糊控制步骤设计整个控制系统。 笔者研究的单容水箱液位工艺流程如图2所示。

图2 单容水箱液位工艺流程

利用液位计检测实际液位h，当实际液位h达到液位设定值h0时注水调节阀关闭，停止注水；当实际液位h低于液位设定值h0时， 注水调节阀工作；当实际液位h高于液位设定值h0时，注水调节阀关闭，出水调节阀打开。 当实际液位h高于液位设定值h0的差值e较大时， 出水调节阀的开度较大，出水较快；当实际液位h低于液位设定值h0的差值e较大时，注水调节阀开度较大，进水较快。最终使得实际液位h稳定在液位设定值h0［9］。

2.1 输入输出变量选取

输入变量即观测量，输出变量即控制量。 假设液位设定值为h0，液位的实际值为h，则液位的偏差e=h0-h。 如果h0不是恒定值而是随时间变化的函数，则e也是随时间变化的函数，此时的偏差变化率ec=de/dt，由于e和ec为输入变量，故也称为观测量， 观测量有几个就称为几维模糊控制器。所以模糊系统是一个实值向量向一个实值标量所做的二输入一输出映射［10］。 本项目中的液位设定值h0=0.5sin（5t）是随时间变化的函数。 在e的论域上定义语言变量“误差E”，在ec的论域上定义语言变量“误差变化率EC”，控制量u所对应的语言变量为“控制量U”。

2.2 输入变量和控制量的模糊化

偏差e、 偏差变化率ec和控制量u的模糊集合分别定义为E=EC=U={NB，NM，NS，ZO，PS，PM，PB}={负大，负中，负小，零，正小，正中，正大}。 为简单起见，选择量化因子ke和kec为1，比例因子ku为1，这样值域和模糊论域就完全一样。e和ec的值域 为［-0.3，0.3］，输 入 论 域 为{-0.3，-0.2，-0.1，0.0，0.1，0.2，0.3}。 控制量u的值域为［-30，30］，输出论域为{-30，-20，-10，0，10，20，30}。

2.3 确定输入变量和输出变量的隶属度函数

模糊集合中各元素的隶属度函数用Matlab得到。

2.4 建立模糊控制规则

语言变量E和EC的模糊集合中各有7个元素，所以模糊控制规则共有49条。 根据单容水箱液位随动的特性建立的模糊控制规则见表1［11，12］。 确定模糊集合的隶属度函数和模糊控制规则之后，就可以计算49 条模糊控制规则所对应的模糊关系。

2.5 模糊推理

二维模糊控制器所采用的模糊规则形式为：

表1 模糊控制规则

上述模糊规则可以总结为：IF A and B THEN C的形式，其中A和B为输入论域上的模糊子集。

确定上述规则的模糊关系Rl（l=1，2，…，49），共49条规则对应49种模糊关系，总模糊关系矩阵R=R1∪R2∪…∪R49。 总的控制量U=（A×B） R，由此可以确定输出的模糊集合U，将U解模糊化得到最终控制量u的输出。

2.6 解模糊

上述模糊推理得到的控制量是一个模糊集合， 而不是真正的物理量的实际精确值输出，将输出的模糊集合控制量转换为物理上的精确值的输出即解模糊，因为只有物理上的精确值才能驱动执行器，所以需要解模糊。 解模糊的典型方法有3种：最大隶属度法［13］、重心法和加权平均法，本项目采用最大隶属度法。

3 基于Matlab的模糊控制系统仿真

3.1 被控对象数学模型

3.2 隶属度函数仿真

由Matlab得到的模糊推理系统和模糊集合隶属度函数如图3～6所示。

3.3 建立模糊控制系统

当模糊集合的隶属度函数和模糊规则确定之后，整个模糊推理系统建立完毕。但要实现模糊控制系统的仿真， 需要将建立的模糊推理系统嵌套到模糊控制器中。嵌套到模糊控制器的步骤如下：

图3 模糊推理系统

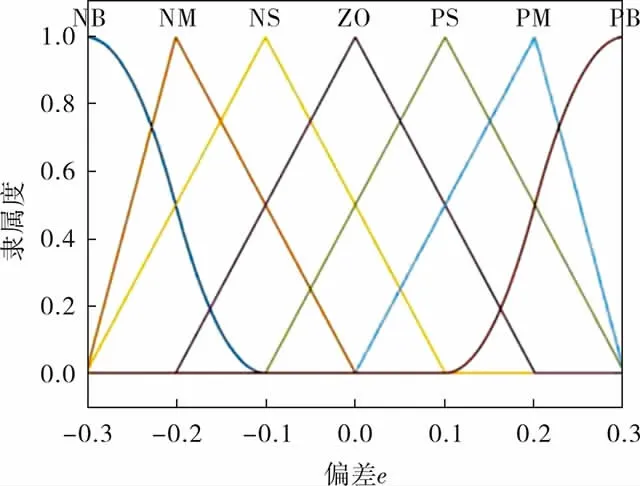
图4 e的隶属度函数

图5 ec的隶属度函数

图6 u的隶属度函数

a. 生成模糊推理系统的FIS文件；

b. 将FIS文件送入Matlab的工作空间；

c. 将工作空间中的FIS文件导入模糊控制器［14］。

笔者建立的整个模糊控制系统如图7所示。

3.4 随动系统液位跟踪仿真效果

将生成的FIS文件导入图7所示的模糊控制器，得到图8所示的跟踪效果图。 可以看出，笔者设计的模糊控制系统实现了单容水箱液位随动的跟踪，跟踪效果较好，说明模糊控制可以应用于非线性控制和系统模型不确定的场合。 但也有缺点，即随着输入变量的增加，控制规则将增加，实现较困难。

图7 模糊控制器

图8 单容水箱液位随动跟踪效果

4 结束语

从仿真结果可知，模糊控制系统对单容水箱液位随动的跟踪效果较为理想， 相比于传统PID控制方法的恒值控制，模糊控制系统不仅能实现恒值控制，还可以实现非线性控制。 但是在曲线的波峰和波谷位置实际液位的跟踪效果不是很理想，还需要进一步改进。