基于小波阈值去噪的管道泄漏检测研究

张 勇 段运达 王 臣 姚岱男 姜鑫蕾

（东北石油大学物理与电子工程学院）

国内外超过50%的已铺设管道运行时间超过了30年，不可避免的腐蚀问题导致了管道存在泄漏风险，造成资源的浪费和环境污染。 近几年，虽然国家出台了相关法律法规严打偷油盗油行为，但是仍有人顶风而上违法盗取国家资源。 管道安全问题越来越受到相关企业的重视，对管道运行时的泄漏信号进行处理和分析，从而准确快速地定位泄漏点成为研究热点。 管道运行时会受到自身或者外界噪声干扰，使得管道运行压力信号波动，而管道泄漏信号常伴随着噪声信息，因而增加了信号处理的难度，采用有效的方法对含噪泄漏信号去噪进而实现管道泄漏点的准确检测意义重大。

傅里叶变换是最早的信号处理方法，相较于传统的傅里叶变换方法，小波变换可以很好地处理信号的高频信息，在去噪过程中优势更明显［1］。

1 小波变换

1.1 基本原理

小波基函数φ（t）经过傅里叶变换后可以得到ψ（ω）。 设小波基函数φ（t）∈L2（R）满足下式［2，3］：

小波基函数φ（t）经过平移和伸缩后可得：

式（3）中，随着a的值越来越小，信号x（t）在b邻域范围也会逐渐变小形成尖脉冲。 选取恰当的尺度因子a，Wx（a，b）能够计算出信号x（t）在b附近的局部信息，进而实现对异常点的检测。

1.2 小波变换的特点

小波变换是傅里叶变换思想的升级，窗口大小变化得到改善。

选取合适的小波基，时域和频域的局部信息都可以被分析，可以更好地检测信号的异常点。

小波具有多分辨率分析的能力［4］，可以同时对信号时域和频域进行分析，去噪效率更高。

2 小波阈值去噪

小波阈值去噪原理简单、去噪效果良好［5］，因此被广泛应用于众多领域。 阈值函数、阈值选取和小波分解层数共同影响该方法的去噪效果。

笔者利用小波变换对采集到的含噪声管道泄漏信号进行去噪，针对常用的小波阈值去噪特点提出新的阈值函数，并给信噪比选取了合适的阈值和小波分解层确定方法，确定最优的去噪方式。 最后，在实验室进行试验分析。

2.1 改进的阈值函数

管道泄漏信号处理时往往受到大量噪声的干扰。 经小波分解后有用信息与干扰信息分布在不同区域，利用数学方法选取合理的阈值，可以把高频和低频区域的小波系数分离，通过满足阈值条件保留有用的泄漏信息，对保留下的有用小波系数进行小波逆变换重构。 小波阈值去噪方法对管道泄漏信号进行处理的流程如图1所示。

图1 小波阈值去噪方法处理管道泄漏信号的流程

传统的阈值函数有硬阈值函数和软阈值函数［6］，分别为：

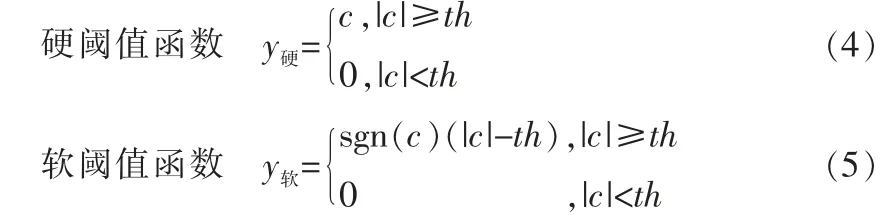
其中，th为阈值，c为高频小波系数。这两种阈值去噪方法已经得到应用，但是硬阈值方法处理信号过程中存在间断点可能产生新的噪声，软阈值方法弥补了这个缺点，有效地处理了边界不连续部分， 但由于和最初小波系数之间存在偏差，在处理过程中一些有用信息会丢失。

在处理过程中两种方法都存在不足，为此提出一种新的管道信号去噪阈值函数：

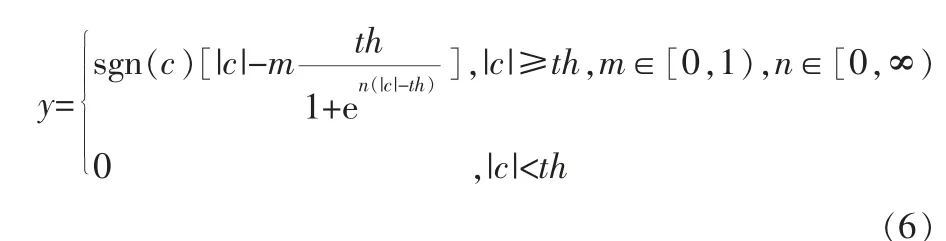
对式（7）进行分析可知，在c→∞的过程中y不断趋近于sgn（c），y是以y=sgn（c）为渐近线的，可以减小软阈值函数中出现恒定偏差而造成的影响。

对比软阈值和新阈值函数的去噪效果，选取db5小波基函数利用软阈值方法和新阈值方法对图2所示的管道泄漏压力信号进行K1～K8尺度分解，信号处理后的信噪比见表1。 信噪比［7］是小波去噪质量的直观体现，信噪比的值越大说明去噪效果越好。

图2 管道泄漏压力信号

表1 K1～K8尺度分解去噪结果

由表1可以直观地看出， 新的去噪方法去噪效果更好，且不论在哪一尺度下新的去噪方法都比软阈值去噪方法的信噪比高。

2.2 阈值的选取

在对管道泄漏信号的处理中，阈值的选取是区分泄漏信息和干扰信息的重要一步，阈值选取不当会影响处理结果， 反而增加信号处理难度。常用的阈值选取方式为Donoho D L等于1994年提出的通用阈值th［8］：

其中，σ为方差，N为信号长度。

表2 4种阈值选取处理对比

2.3 最优分解层分析

在小波去噪过程中，小波的分解层数也影响着去噪效果［9］。 以信噪比为例，分解层数较小，去噪后的信噪比较低，去噪效果不理想。 而分解层数过大，不仅早生信息被剔除，有用信息也会被滤掉，导致信噪比降低。 小波变换进行信号处理时，固定的分解层应用广泛，但是管道泄漏复杂多变，不同的泄漏信号小波分解层数相同但去噪效果却有所不同，所以小波阈值去噪时小波分解层数的自适应选取也很重要。 自适应最优分解层选取方法主要是基于噪声检验和最优信噪比的方法。

基于噪声检验［10］确定最优分解层的方法步骤如下：

a. 令小波分解层数k=1，进行小波分解，提取近似系数和高频系数；

b. 对高频系数进行白噪声特性检验，若高频系数检测为噪声特性，则转至步骤a进行k+1层小波分解，否则进行步骤c；

c. 若检测无噪声特性，输出最优分解层数k-1。

a. 令小波分解层数k=1，进行小波分解，提取近似系数和高频系数；

b. 用阈值函数对高频系数处理重构；

c. 计算ΔEk和ΔEk-1，k＞1；

d. 若ΔEk＜ΔEk-1则返回步骤a， 若ΔEk≥ΔEk-1则输出最优分解层数k-1。

利用上述两种方法对两次管道泄漏信号（图3、4）去噪得出的最优分解层数分别为5、5和6、5，通过计算得出不同尺度下的去噪效果见表3。

图3 泄漏信号1

图4 泄漏信号2

表3 不同尺度下的去噪效果

3 试验分析

试验数据来源于实验室真实搭建的小型油气管道平台，如图5所示。

图5 油气管道平台

管道总长182.68m，共有18个泄漏点，其中4个为电动阀其余为手动阀。 试验时，通过增压阀对管道进行打压直到满足试验条件，通过手动开阀试验进行泄漏信号的采集， 并控制泄漏口径，得到不同泄漏情况的数据。 选取5号和10号阀门进行试验并控制两个阀门的泄漏情况，5号阀门与10号阀门的实际位置为51.85、101.58m， 对5号阀门进行大口径快速泄漏操作，10号阀门缓慢泄漏操作。 图6、7分别为5号点和10号点原始泄漏波形和阈值去噪后的波形。

图6 5号阀泄漏波形和去噪后的波形

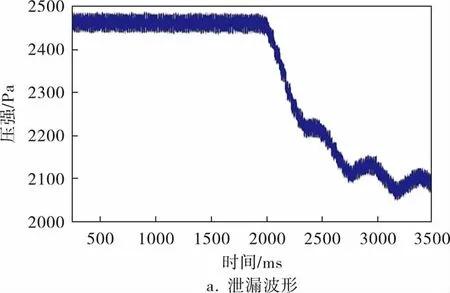
图7 10号阀泄漏波形和去噪后的波形

由图6、7可以清楚地看出， 新方法下两种开泄情况去噪效果良好，输出波形平滑。

笔者利用负压波法［11］实现泄漏点的定位，该方法在管道两端分别安装压力传感器，通过确定传感器接收信号的时间差和波速来计算泄漏位置。 5号与10号泄漏点随机5次的泄漏定位数据见表4。

可以看出，定位的相对误差有起伏，并不是每一次都非常精准，通过对每个泄漏阀进行大量的开泄试验分析计算，该方法下泄漏位置的平均相对误差在3.0%以内。

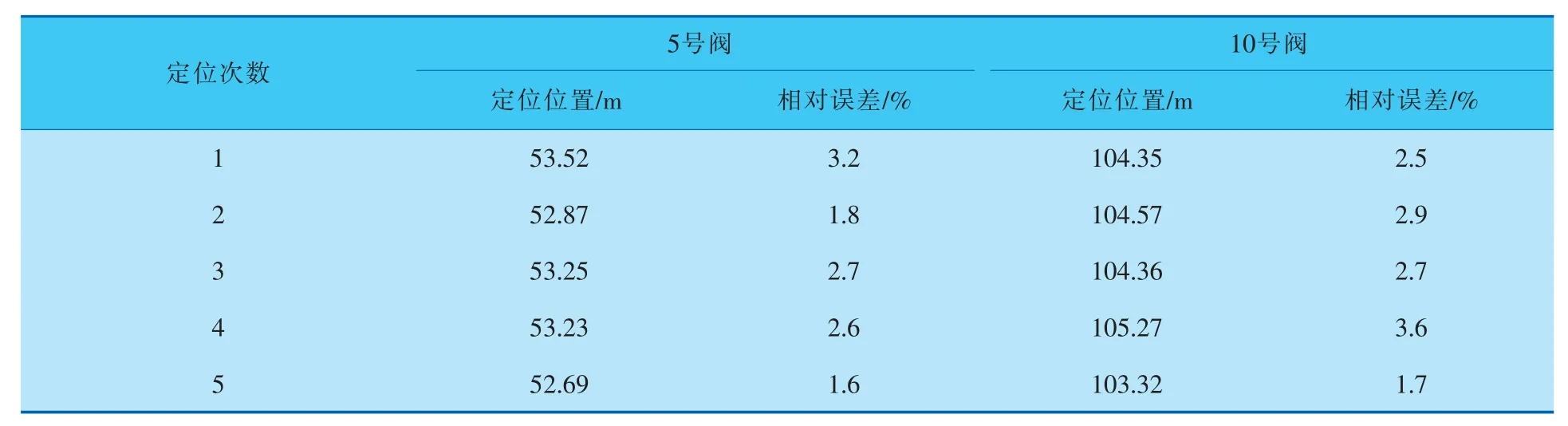
表4 泄漏定位数据

为了更直观地体现新阈值函数作用下的定位效果， 同时利用软阈值去噪法去噪进行定位，两种处理方法20次定位结果对比如图8所示。 可以明显看出笔者方法定位更加准确，试验的定位结果并不是每次都很精准，也会有波动，但属于个别现象。 比较而言，笔者方法相对软阈值方法波动较小、准确度高且更加稳定。

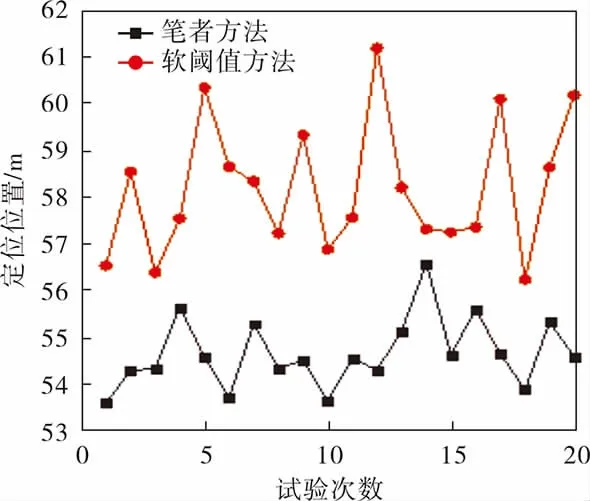
图8 两种方法的定位结果对比

4 结束语

对于管道泄漏信号处理，小波阈值去噪方法可以有效去除管道泄漏信号中的噪声干扰。 笔者在分析软、硬阈值去噪方法的基础上，提出新的管道泄漏检测去噪阈值函数，基于信噪比的情况与软阈值函数去噪效果进行比较，笔者算法去噪效果更好。 通过对比，选取更适合管道泄漏检测的自适应小波最优分解层方法，确定了小波最优分解层。 最后比较该方法下去噪后和软阈值去噪方法去噪后管道泄漏位置的定位，通过去噪后的定位结果精度比较，新的阈值函数去噪相比传统的小波去噪方法去噪效果更好。 利用该方法去噪定位，平均相对误差在3.0%以内。 由于实际工况下管道所处环境恶劣，有时还有突发情况，还需进一步深入研究小波理论在管道泄漏检测中的应用。