动车组设备多目标预防性维护间隔期研究
2021-04-28刘志龙
熊 律,王 红,刘志龙
(1. 兰州交通大学 机电工程学院,兰州 730070;2. 广东交通职业技术学院 轨道交通学院, 广州 510650;3. 中国铁路成都铁路局集团有限公司,重庆 400000)
随着我国高速铁路的高速发展,每年都会有大量的动车组投入运营使用,随之而来的是大量且复杂的维护工作,这为动车组设备维护领域的工程师和研究者提供了广阔的研究天地.贺德强等[1]综合分析机会役龄因子和安全失效概率因子对PM策略的影响,在传统PM策略基础上,提出了一种基于可靠性的列车关键部件机会PM优化模型.YU等[2]基于改进的二代非支配排序遗传算法,对高速铁路接触网失效模式进行分析,建立了系统可靠性与PM成本之间的优化模型.此外,以可靠度为中心的动车组设备PM策略研究也受到了学者们的青睐[3-6].熊律等[3]为了降低动车组部件在一个寿命周期内的维修总成本,以动车组五级修程时需要更换的部件为研究对象,基于现行的分级检修制度,提出一种动车组部件多级非完美维修预防性维修策略.王红等[4]通过引入动车组部件故障风险量化机制,以PM可靠度阈值为优化目标,以PM总成本为优化目标,建立了一种考虑故障风险的动车组多部件系统机会维护优化策略.杨国军等[5]为了探究不同运量需求影响下动车组复杂系统成组维修策略,引入运量需求因子描述动态运量需求,建立考虑运量需求的设备维修调整成本模型,基于动态成组方法对设备维修活动进行合并,构建考虑运量需求的动车组复杂系统动态成组模型.XIONG等[6]以高速铁路动车组运营方和维护方为博弈的参与者,以动车组部件PM可靠度阈值作为讨价还价的对象,分别建立了运营方优先出价和维护方优先出价的三阶段讨价还价动态博弈模型.上述文献在为动车组设备制定PM计划时,其优化目标虽不尽相同,但都是单目标优化,即优化目标都是唯一的.然而,对于动车组这类成本昂贵且体积庞大的设备,在期望降低其维护成本的同时,也期望其可用度能尽可能提升,故考虑引入多目标优化决策模型.
实际上,多目标维护决策,在生产设备的PM研究中有着广泛应用[7-11].刘洋等[7]以复杂机电产品为研究对象,基于非等检测周期、多阶段预防性维修、多目标维修等维修策略,分别以产品可用度、可靠度和运维成本为优化目标,开展多目标维修决策优化研究.刘勤明[8]等针对考虑库存缓冲区的多目标设备维修问题,以设备维修能力为约束条件,获得随机故障设备的不完美预防维修策略.LIU等[9]认为商品库存数量和生产设备的维修间隔期具有关联关系,为了取得二者之间的平衡,提出了一种综合考虑商品库存量和设备PM间隔的多目标PM策略.吕言[10]从可靠性与维护优化基本理论出发,结合多目标优化等相关领域在维护优化方面的研究成果与实践,对核电站预防维护过程进行相关假设,构建了以设备可用度、设备可靠度、设备成本为目标函数的设备级多目标预防维护优化模型.
本文以动车组设备维护成本率和可用度作为优化目标,对动车组设备的PM采用两级非完美维修策略,以效费比作为经济性评价方式决策每一次维护的具体方式,以PM成本、小修成本和停机损失为维护总成本,建立动车组设备多目标PM间隔期决策模型.并通过算例分析,对单一维护成本率决策模型、单一可用度决策模型和多目标优化决策模型计算结果进行对比分析,进而验证所提出模型的有效性并得出结论.
1 模型的建立
根据既定的维护策略,PM发生在设备的可靠度达到阈值R时,即进行PM时设备的可靠度为R,其可靠度方程[6]为

(1)
式中,Ti为PM之间的时间间隔;λi为设备的故障率函数,t为时间变量.
1.1 两级非完美维护故障率演化模型
由混合式故障率演化模型[4]可知,维护前后设备故障率函数之间的关系可定义为
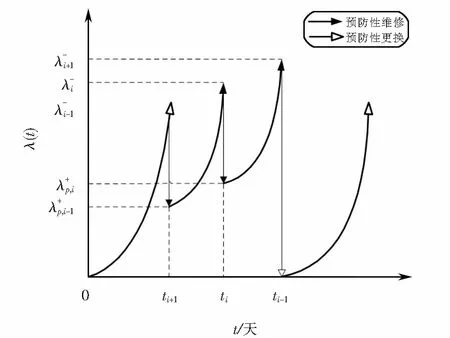
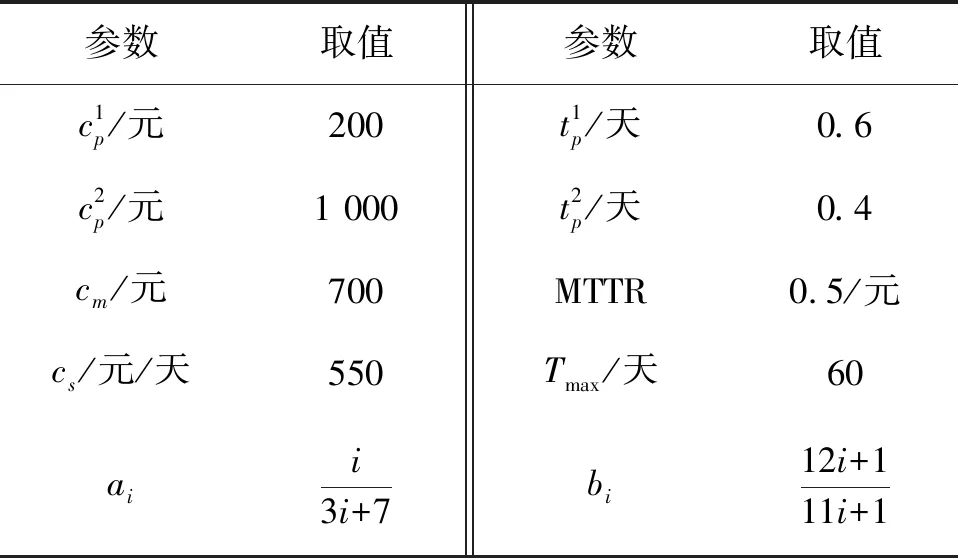
λi+1(t)=biλi(t+aiTi),0 (2) 设备的维护成本主要包括PM成本Cp、非预期故障导致的小修成本Cr和设备的停机损失Cd,设备一个更换周期内维护总成本C的表达式[6]为 C=Cp+Cr+Cd. (3) 1.2.1 预防性维护成本 假如设备在第N次PM时执行更换操作,则其一个更换周期内的预防性维护成本可表示为 (4) 图1 故障率演化Fig.1 Failure rate evolution 1.2.2 小修成本 假设设备单次小修的平均成本为cm,则设备在一个更换周期内的小修成本[4]为 (5) 1.2.3 停机损失 当对设备执行PM和小修操作时,设备需要停止运行,此时,会产生停机损失Cd如下 (6) dt)MTTR]. (7) 1.3.1 维护方式 在此引入维护方式选择因子ω[4],其表达式为 (8) 对设备采取预防性维护或预防性更换之后,设备的故障率演化也有所不同[4] a=(1-ω)ηp+ωηg, (9) b=(1-ω)θp+ωθg. (10) 式中,ηp和ηg分别表示执行预防性维护和预防性更换后的役龄递减因子,0<ηp<1,ηg=0;θp和θg分别为执行预防性维护和预防性更换后的故障率递增因子,θp>1,θg=1. 1.3.2 维护方式的选择 本文以效费比作为设备维护经济性的评价指标[4],则有 (11) (12) (13) 式(8)可进一步表示为 (14) 论文中目标函数主要包括设备在一个更换周期内的维护成本率CR和可用度A. 设备在一个更换周期内的维护成本率为维护总成本与运行时间和停机时间之和的比值,维护成本率CR可表示为 (15) 设备在一个更换周期内的可用度为运行时间与运行时间和停机时间之和的比值,设备可用度A可表示为 (16) (17) 式中,A*为可用度的最优值,CR*为维护成本率的最优值. 威布尔分布广泛应用于机械电子产品的故障率描述[6],其表达式为 (18) 式中,β为形状参数;η为生命特征参数,β和η可通过对历史故障数据的分析得出,取β=2.5,η=100. 其它参数的取值依据文献[12-15],如表1所示. 表1 参数设置 表2是单一维护成本率模型、多目标决策模型和单一可用度模型的优化结果;图2、图3和图4分别为三种模型的维护成本率和设备可用度与维护时间间隔之间的关系. 表2 优化结果 由表2可知: 1) 对于单一维护成本率模型,当维护时间间隔T=26天且在第12次维护时执行更换操作可使得设备的维护成本率CR最低(如图2(a)所示),此时其可用度A也最低(如图2(b)所示).且由于其维护时间间隔T最小,即其维护频率最高,故其故障小修次数也是三种维护模型中最少的. 2) 对于单一可用度模型,当维护时间间隔T=35天且在第12次维护时执行更换操作可使得设备可用度A最高(如图3(a)所示),此时其维护成本率CR也最高(如图3(b)所示).由于其维护时间间隔T最大,即其维护频率最低,故其故障小修次数也是三种维护模型中最高的. 3) 对于多目标优化决策模型,当维护时间间隔T=27天且在第12次维护时执行更换操作可使得目标函数V最小,此时其维护成本率CR并非最小(如图4(a)所示),可用度A也不是最大的(如图4(b)所示),其维护时间间隔T和故障小修次数介于其他两种模型之间. 由图5三种维护模型结果对比可知,多目标优化决策模型和单一维护成本率模型的维护成本率优化结果十分接近,但多目标优化决策模型的设备可用度优化结果优于单一维护成本率模型.多目标优化决策模型的可用度优化结果低于单一可用度决策模型,但是其维护成本率也明显低于后者.单一维护成本率模型的维护成本率明显低于单一可用度决策模型,略低于多目标优化决策模型,但是其可用度优化结果明显低于其余两种模型,即单一维护成本率模型为了达到目的,需要牺牲一部分可用度需求.单一可用度模型的可用度优化结果优于其余两种模型,但是其维护成本率也明显的高于其余两种模型,即单一可用度模型为了保证设备的可用度,需要降低对设备维护经济性的要求. 图2 单一维护成本率模型(w1=0,w2=1)优化结果Fig.2 Optimization results of single maintenance cost rate model (w1=0,w2=1) 图3 单一可用度模型(w1=1,w2=0)优化结果Fig.3 Optimization results of single availability model (w1=1,w2=0) 图4 多目标优化决策模型(w1=0.5,w2=0.5)优化结果Fig.4 Results of multi-objective optimization decision model (w1=0.5,w2=0.5) 图5 三种维护模型优化结果对比Fig.5 Comparison of optimization results of the three maintenance models 论文以维护成本率和设备可用度作为优化目标,建立了单一维护成本率模型、单一可用度模型和多目标优化决策模型,并通过对比分析得出以下结论: 1) 单一维护成本率模型的维护成本率优化结果是三种模型中最低的,但其可用度优化结果也是三者中最低的.故单一维护成本率模型可用于对维护经济性要求较高,对可用度要求较低的动车组设备制定PM计划. 2) 单一可用度模型的可用度优化结果是三种模型中最高的,其维护成本率优化结果也是三者中最高的.故对于可用度要求较高,对维护经济性要求较低的动车组设备,单一可用度模型能更好的满足需求. 3) 多目标优化决策模型的维修成本率和可用度优化结果均介于其余两种模型之间,故对于维护成本率和可用度均有要求的动车组设备,多目标优化决策模型是更优的选择.并且相对于单一维护成本率模型,多目标优化决策模型可在维护成本率相当的情况下,使动车组设备的可用度保持在更高的水平.
1.2 维护成本建模

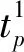
1.3 维护方式的选择

1.4 目标函数
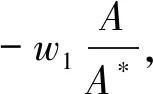
2 算例分析





3 结论
