基于改进多尺度排列熵的S700K转辙机故障诊断
2021-04-28魏文军
李 政,魏文军,2
(1. 兰州交通大学 自动化与电气工程学院,兰州 730070; 2. 兰州交通大学 光电技术与智能控制教育部重点实验室,兰州 730070)
S700K转辙机是实现铁道线路转换的关键机电设备,占40%的铁路信号设备故障由S700K转辙机引起,严重危及行车安全.随着铁路运行密度和行车速度的提升,对S700K转辙机故障诊断精度和效率提出了更高要求.当前S700K转辙机故障检修主要依赖于计划型检修,凭人工经验判断故障类型,存在过剩维修、劳动效率低以及安全风险大等问题.近年来,基于信号集中监测系统实时监测转辙机动作功率曲线,利用信号时序特征的S700K转辙机故障检测已成为热点研究方向.S700K转辙机故障诊断可分为故障信息提取和故障诊断两大步骤,在故障信息提取方面,文献[1]采用经验模态分解(empirical mode decomposition,EMD)和小波包分解(wavelet packet transform,WPT)相结合方法,将分解分量的包络特征作为故障信息,但原始信号序列经分解后的包络特征单一,影响后续故障分类精度.文献[2]利用费雷歇距离公式计算各个样本曲线和故障曲线之间相似度,将相似度最大的样本曲线作为故障诊断的输出,但干扰对此种方法的影响大,而转辙机运行受到室外环境的影响,干扰无法避免.在故障诊断方面,文献[3]根据门限要求,通过计算样本集和故障集的灰关联度来识别故障类型,但门限值的选择需要人工经验,影响故障诊断率.文献[4-5]基于卷积神经网络对不同故障类型进行精确识别,缺点是训练网络参数需要大量的数据,而道岔的故障发生率低,收集大量数据的代价较高.文献[6]提出利用专家系统建立故障诊断模型,但存在现场更新知识库比较困难,实用性差.
综上所述,当前S700K转辙机故障诊断具有故障特征提取不足和小样本分析的特点.在诊断算法中,支持向量机具有处理小样本、非线性故障分类的独特优势,并已成功应用于航空发动机、变压器、滚动轴承的故障诊断[7-10].在特征信息提取中,集合经验模态分解(ensemble empirical mode decomposition,EEMD)分解和小波分解适用于处理非平稳、非线性信号,具有自适应性、对局部特征敏感[11-15]的优势.多尺度排列熵用于表征信号序列的复杂度,并已成功应用于电机轴承、列车轴箱等振动信号特征信息的提取[16-18].
基于信号集中监测系统中的S700K转辙机功率曲线,提出一种融合EEMD分解和小波分解的改进多尺度排列熵故障诊断算法.首先,利用EEMD分解和小波分解对S700K转辙机动作功率曲线进行分解,并以多尺度排列熵建立故障特征集;然后,为减少信号冗余,将故障特征集进行核主元分析(kernel principle component analysis,KPCA)处理;最后,基于多变量支持向量机算法实现对S700K转辙机的故障诊断.
1 S700K转辙机功率曲线分析
1.1 动作功率曲线与运行状态的关系
S700K转辙机由室内控制电路和室外动作电路共同作用完成道岔转换,其电机的输出功率P和拉力F为:
(1)
(2)
由式(1)~(2)可得,S700K转辙机动作功率和拉力特性关系为
(3)
式中:Re、n、η为S700K转辙机内置参数,分别表征等效力臂、转速和转换效率.由此可得,S700K转辙机动作功率曲线反映其拉力的大小,通过分析道岔在转换过程中S700K转辙机动作功率曲线,可获取道岔运行状态及机械性能.
TJWX-2006型信号集中监测对道岔转换过程中电流和电压进行实时同步监测,通过式(4)实现转辙机动作功率曲线的采集.图1为S700K转辙机正常动作功率曲线.
(4)
式中:u、i分别为S700K转辙机动作瞬时电压、电流;T为S700K转辙机动作运行时间;N表示采样点个数.
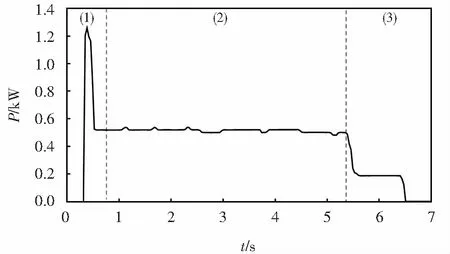
图1 S700K转辙机正常动作功率曲线Fig.1 Normal operating power curve of S700K turnout
S700K转辙机正常动作时间为6.6 s,尖轨运动距离150~220 mm[16],40 ms为动作功率曲线的采样周期.以定位到反位为例,按照S700K转辙机动作过程,其功率曲线可以大致分为以下三部分:
1) 启动和解锁:道岔启动继电器接通,同时断开道岔定位表示电路,转辙机电机得电.电机反转带动齿轮组和摩擦联结器使得滚动丝杠逆时针转动,动作杆完成解锁状态.因电机属于硬启动,此时动作瞬时功率比较大.
2) 转换过程:启动继电器继续接通,使得电机继续带动滚动丝杠逆时针旋转,道岔从定位向反位移动,当尖轨移动220 mm时完成道岔转换过程,此时S700K转辙机功率曲线比较平稳.
3) 锁闭:因为启动继电器具有缓放特性,B、C两相电流和整流堆构成回路,同时接通道岔反位表示电路,此时S700K转辙机动作功率曲线出现“小台阶”后降为零.
1.2 典型故障曲线及分析
本文通过对兰州铁路总公司信号集中监测中心的调研,调研了龙泉寺、骆驼巷和哈达铺等9站的S700K转辙机故障动作功率曲线记录.针对现场真实故障数据进行分析,总结在典型故障动作功率曲线下的S700K故障类型,如图2所示,对应的转辙机故障分析如表1所示.以图2中5种典型功率曲线为例进行算法可行性分析,并在此基础上对其他S700K转辙机故障类型具有推广性.
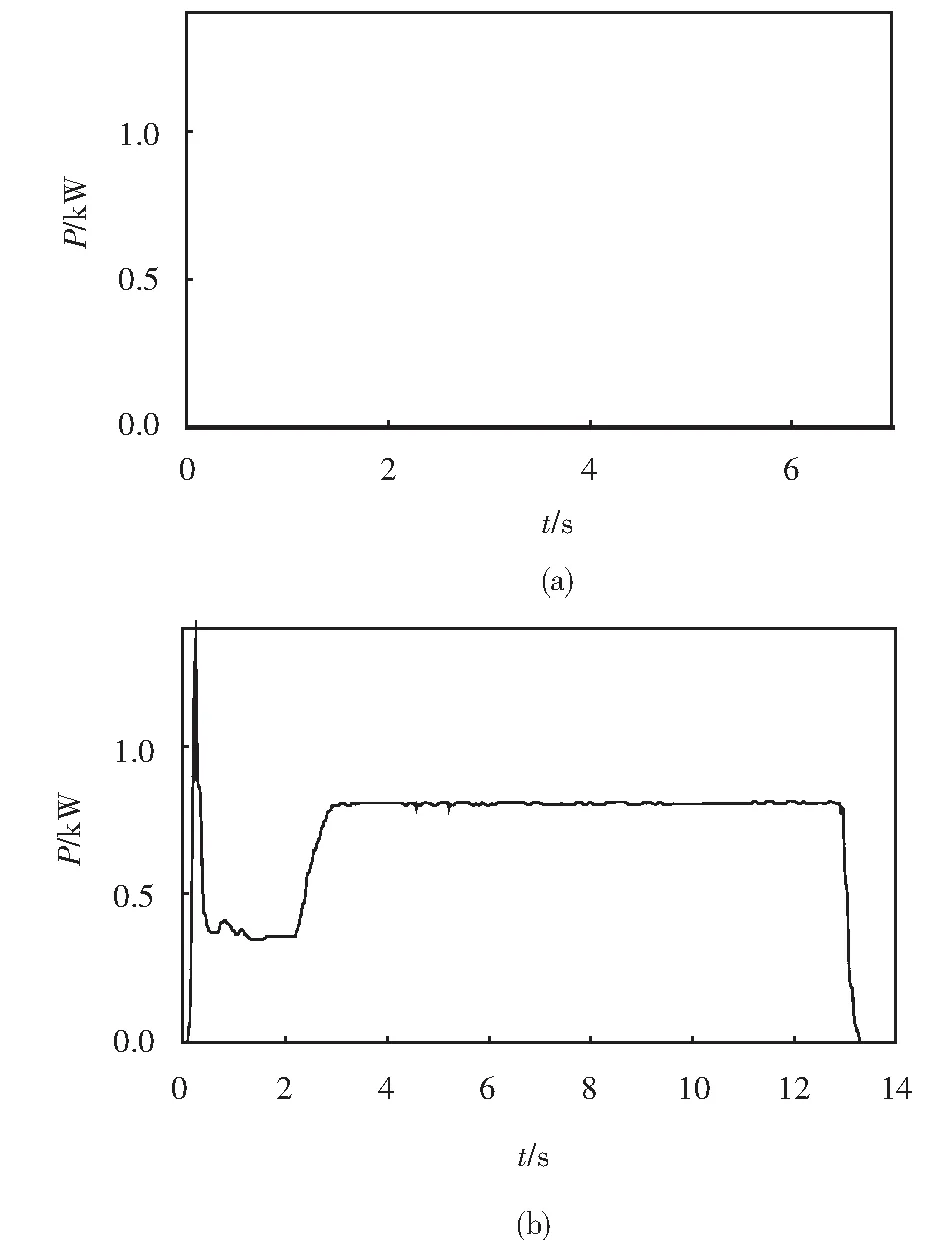
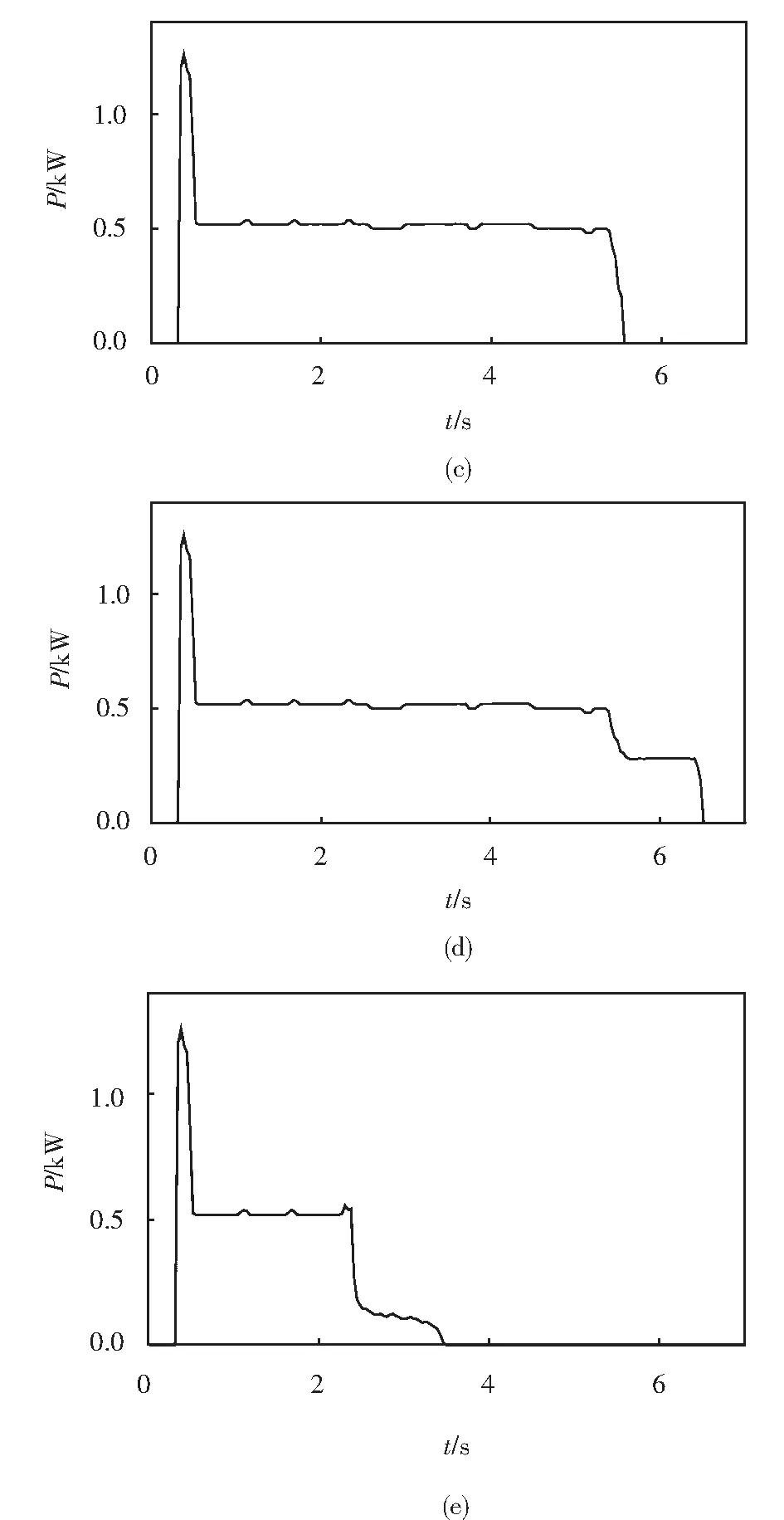
图2 典型故障功率曲线Fig.2 Typical fault power curve
2 基于EEMD和小波分解的改进多尺度排列熵的故障特征提取
2.1 EEMD分解
EMD分解方法是一种自适应频域分解[5],与傅里叶分解相比不需要基函数.实现形式是每一模态分量必须满足以下两个条件:
1) 极值点个数和过零点个数误差不超过1个.
2) 上下包络线的均值等于0.
通过多次迭代得到不同分辨率的信号分量,最后剩余分量为单调信号或者没有足够极值点时结束分解,如式(5)所示.
(5)
式中:imfi(t)为原信号的第i个本征模态分量;rn(t)为剩余分量.

表1 S700K转辙机典型故障分析
当信号序列极值点不足时,经EMD分解后存在模态混合的问题,一种模态分量往往存在不同时间尺度.为解决此问题,EEMD分解在进行EMD分解之前,加入n组不同时间尺度下的正态高斯白噪声,具体算法流程如图3所示.
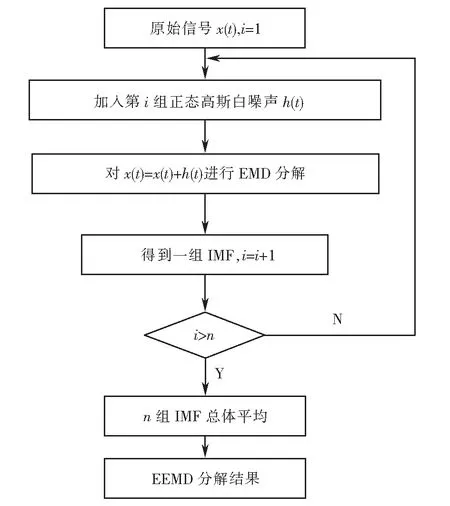
图3 EEMD分解流程图Fig.3 EEMD decomposition flowchart
首先将原始信号x(t)加入均值为零的n组正态高斯白噪声:
xi(t)=x(t)+hi(t),
(6)
其中:i=1,2,…,n.
然后将n组加入高斯白噪声后的信号序列分别进行EMD分解,可得各组模态分量Cij(t)和剩余分量ri(t):
(7)
其中:j为分解层数;i=1,2,…,n.
最后,根据高斯白噪声在时频域上均值为0的特性,对各组模态分量进行均值化处理,得到最终本征模态函数分量(instrinsic mode function,IMF):
(8)
其中:j为分解层数,j=1,2,…,n.
2.2 小波分解
小波分解对原始信号进行频域分析,既有傅里叶分解局部化的特点,又消除了傅里叶分解对频率变化不敏感.定义小波基函数ψ(t)满足的条件是

(9)
小波分解与傅里叶分解相对比,将基函数变成可以伸缩和平移的连续小波函数:
(10)
其中:a,b∈R,a≠0,a为缩放尺度,b为平移尺度.基函数缩放尺度对应窗口频率,平移尺度对应窗口时间,将其与原始信号不断相乘,得到相应尺度下原始信号的分解分量.小波分解公式如下:
(11)
S700K转辙机功率曲线具有突变特性,本文选择满足紧支性和正则性的Mallat快速算法作为小波基,其分解算法如公式(12)所示.
(12)
式中:m为离散采样点,m=1,2,…,N;Cj(k)为分解后的近似分量;Dj(k)为细节分量;hn、h1n为滤波器函数;k∈Z.
2.3 改进多尺度排列熵算法
多尺度排列熵用于分析信号序列的复杂程度,当信号序列越不规则,其排列熵值越大.设时间尺度为τ,多尺度排列熵算法流程如下:
1) 一维信号序列为x(t)(t=1,2,…,N),对其进行粗粒化处理:
(13)
式中:1≤j≤[N/τ],N为采样点个数,τ为计算时间尺度,[N/τ]为取整函数.
2) 将粗粒化后的信号序列进行排序,映射到τ!种排列序号中,进而计算多尺度排列熵:
MPE(x,τ,m,δ)=PE(y,m,δ).
(14)
其中:PE(permutation entropy)为排列熵值;MPE(multi-
scale permutation entropy)为多尺度排列熵值;m、δ分别为嵌入维度和时延参数.
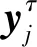
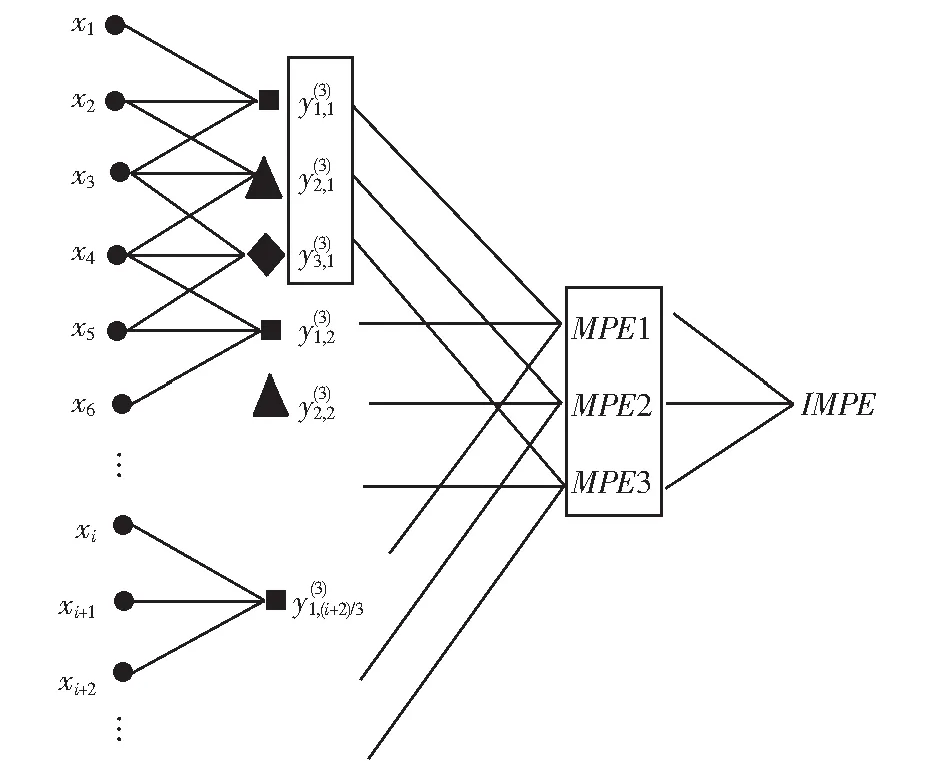
图4 改进多尺度排列熵示意图Fig.4 Schematic diagram of improved multi-scale permutation entropy
1) 以(x1,x2,…,x1+τ),(x2,x3,…,x2+τ),(x3,x4,…,x3+τ),…,递增的方式组成不同粗粒化序列,如式(15)所示.
(15)
2) 针对粗粒化结果,求取各自MPE.
(16)
3) 求取MPE平均值.
(17)
实际应用中嵌入维度m的选择决定了计算量和精准度的大小.文献[13]中取N≥5m!,根据采样序列N=300,可知m取4.
2.4 故障特征集的建立
以图2中故障(b)为例,根据EEMD分解、小波分解和改进多尺度排列熵算法,建立故障特征集:
Step1:EEMD分解后的结果如图5所示.其中C1~C4为EEMD分解分量,C5为剩余分量,并满足剩余分量为单调信号或者没有足够极值点的终止条件.
Step2:根据小波分解算法,对故障动作功率曲线进行5层小波分解,分解结果如图5中D1~D5所示.
Step3:设置时间延时参数δ=11,计算原始信号f及各分解信号的排列熵,从而建立如表2所列的特征集R11×11.
从上述故障特征集可以看出:单个故障特征集维数过多,存在信号冗余,不能作为故障诊断输入信号.为精简信号特征,需要对特征集进行进一步分析.
2.5 数据降维KPCA算法
KPCA最早是由Pearson[10]提出的,通过线性变换,以信号特征之间的相关性,对特征集进行筛选和排序,进而达到信号特征集降维的目的,其算法流程如下:
1) 令R11×11每一列分量为xi,i=1,2,…,11,映射函数ψ:R→F,则映射矩阵为ψ(xi).根据式(18)算出协方差矩阵:
(18)
其中,u为列向量平均值.
2) 协方差矩阵特征方程为
λV=SV,
(19)
其中:λ为特征值;V为特征向量.上式两端同乘映射矩阵得
λ[ψ(x)V]=ψ(x)SV,i=1,2,…,11.
(20)
3) 特征向量V和核矩阵K的元素可表示为:
V=βψ(x),
(21)
K=[ψ(x)ψ(x)].
(22)
式中,β为相关系数.将式(21)~(22)代入式(20)得
NλKβ=KKβ⟹Nλβ=Kβ,
(23)
式中,N为特征矩阵维度.
4) 由上式可得,核矩阵K的特征向量即为故障特征集的特征向量,本文选择输入参数较少的径向基核函数为
ξ(x,y)=exp[-‖x-y‖/(2σ)].
(24)
将K矩阵特征值λi(i=1,2,…,11)降序排列,并计算其累计贡献率np:
(25)
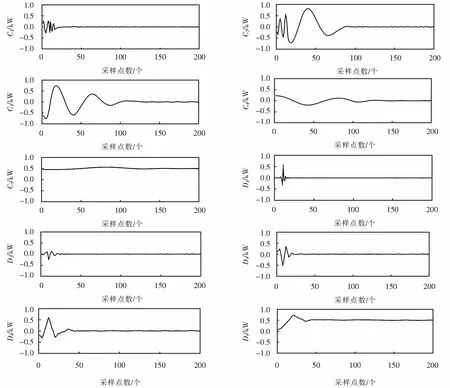
图5 故障(b)EEMD分解和小波分解结果Fig.5 Fault (b) EEMD decomposition and wavelet decomposition results

表2 故障(b)特征集
2.6 故障特征集KPCA分析
提取S700K转辙机动作功率曲线故障特征参数后,为了减少实时计算量,提高计算速度,选用KPCA对故障特征集进行降维,在不损失信号特征情况下表征故障特征.
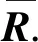
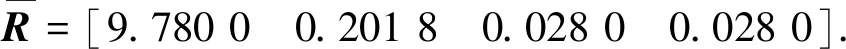
(26)
3 基于多变量支持向量机的故障诊断
3.1 多变量支持向量机故障诊断
支持向量机建立在结构风险和VC(vapnik chervonenkis)理论基础上,VC维度越高,置信度就越低,而KPCA解决了特征集维数过大的问题.引用最优间隔分类器实现SVM二分类,在此基础上运用有向无环图(directed acyclic graph,DAG)方法实现SVM多分类问题[19-21].
1) 以故障(a)和故障(b)为例,构建一个超平面:
wTx+b=0.
(27)
定义故障识别标签为yi,并且故障(a)为+1类,故障(b)为-1类,由此可得:
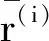
(28)
几何间隔为
(29)
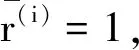
(30)
2) 建立目标函数后,将每个约束条件乘拉格朗日乘子,得拉格朗日函数
(31)
利用拉格朗日的对偶性,对式(31)进行对偶问题求解:
(32)
加入核函数和惩罚变量后,对偶问题等价于:
(33)
最后求得最优间隔超平面为
(34)
3) 多变量支持向量机加入了核函数和惩罚变量,使得其适用于小样本、非线性信号序列的模式识别[22].本文采用有向无环图(DAG)法构造多变量支持向量机,在5种S700K转辙机故障模式下分类结构原理如图6所示,最顶层中1和5相比较,第二层中2和5、1和4相比较,依次类推.
DAG法采用“竞争”法则,对于C种类型时,决策树高度为C减去1,把易于区分的故障放在上层,难以区分的故障放在下层.除叶子结点外,当Dij(x)>0时,x属于i类,否则属于j类.相比较“一对一”、“一对多”分类器数目减少,提高了运算速度.
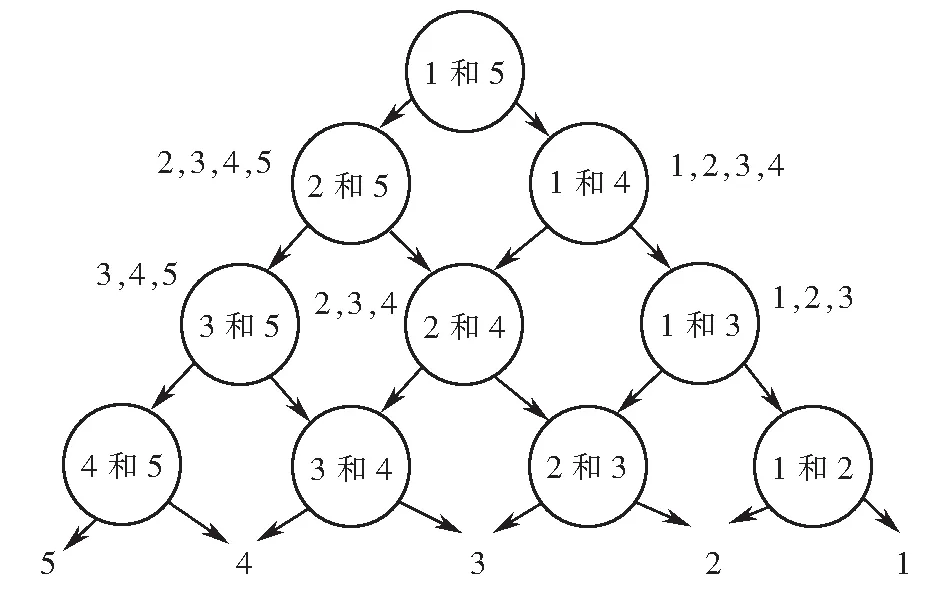
图6 DAG法原理图Fig.6 Schematic diagram of DAG method
3.2 故障诊断流程
基于改进多尺度排列熵和多变量支持向量机(SSVM)的S700K转辙机故障诊断流程为:在采集到S700K转辙机功率信号序列后,根据EEMD理论和小波理论分解各故障模式下的动作功率曲线,分解后的各模态分量体现了故障信号特征.计算各模态分量的排列熵,从而构成故障特征集.利用核主元分析实现故障特征集的降维,并作为SSVM的输入向量,最后实现S700K转辙机故障诊断.
4 实例论证及分析
为了验证该算法的有效性,以兰州铁路总公司信号集中监测存储的龙泉寺、骆驼巷和哈达铺等9站的S700K转辙机动作功率曲线为基础,对故障类别和数据进行整理后,将5种故障模式下各随机抽取20组动作功率曲线的历史记录作为实验数据,100组数据中前60组作为训练样本,后40组作为测试样本.故障标签依次设置为1、2、3、4、5,采用多变量支持向量机算法进行故障诊断,经样本集训练后,40组测试集故障诊断结果如图7所示.
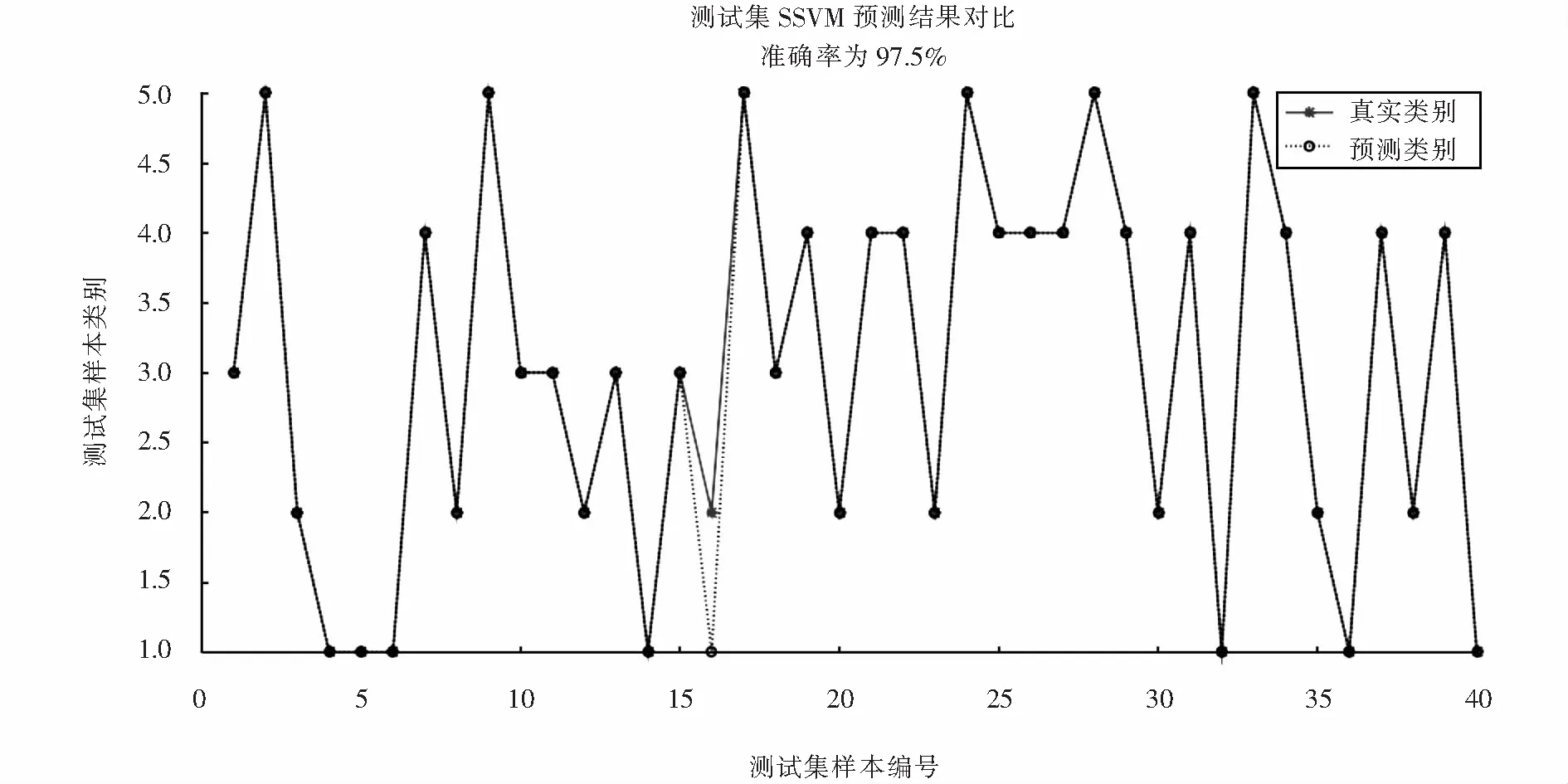
图7 多变量支持向量机故障诊断结果Fig.7 Multi-variable supporting vector machine fault diagnosis results
从图7可以看出,测试集故障诊断率为97.5%,证明了该方法的有效性.利用改进多尺度排列熵算法提取S700K转辙机的故障特征值,并基于SSVM的诊断算法,不仅提高了S700K转辙机的故障诊断率,而且不需要大样本,具有一定的实用性.
5 结论
1) S700K转辙机发生故障时,将其动作功率曲线进行频域分析,EEMD分解和小波分解相结合解决了故障特征不足的问题.
2) 利用改进多尺度排列熵建立故障特征集,更加精准的反映故障信息.采用KPCA分析对故障特征集进行优化,以贡献率为标准,在不损失故障信息情况下,实现故障特征集的降维,提高了故障诊断效率.
3) 基于SSVM故障诊断是根据最优分隔面处理小样本、非线性故障特征向量,最终实现S700K转辙机故障分类.经测试集数据验证,相比较其他分类方式,SSVM分类方法精度更高.
