影响石英单模光纤数值孔径测量的因素及分析

廖红波，李 多

(北京师范大学 物理学系，北京 100875)

随着现代通信技术的发展，光纤在现代生活和科学技术中的应用越来越广泛，光纤原理与应用也成为大学教学的重要内容. 目前，大学物理实验课程中开设的光纤实验主要分为两类：一类是光纤基本参数的测量，比如光纤的数值孔径、损耗系数等[1,2]；另一类是光纤传感技术[3]和光纤通信技术[4]的学习. 物理实验教学中以参数测量和传感技术的应用为主的占多数，因为这两部分更能体现物理知识在光纤技术中的应用，而光纤通信通常在与之相关的工科类专业中开设.

在笔者所在学校开设的光纤实验中，主要以光纤参数(如数值孔径、损耗系数和耦合系数)和光纤温度传感器的温度系数测量为主，光纤通信技术仅作为选做内容. 在教学中，笔者发现不同学生测量得到的商用石英光纤的数值孔径存在着较大的差异，数值在0.08～0.18不等，在排除学生在实验中的错误操作、读数错误、计算错误等因素后，仍然无法消除. 因此本文拟对光纤数值孔径测量中存在的问题进行详细的实验测量和分析，解释导致光纤数值孔径测量差异的原因.

1 光纤数值孔径的定义与测量方法

目前常用商用光纤跳线主要是直径9/125 μm的石英光纤，即光纤的纤芯为直径9 μm的高折射率区，而低折射率的包层直径为125 μm. 光纤在应用时最关键的步骤就是要让光信号尽可能的耦合到纤芯中，以保证信号的强度，而光纤的数值孔径正是决定光纤集光能力的重要参数之一.

1.1 光纤的数值孔径的定义

并不是所有进入光纤中的光线都能在光纤中传播，只有满足全反射条件的光线才能被约束在光纤中进行远程传输. 设在光纤中刚好满足全反射条件的光线的入射角度为θ，则光纤的数值孔径(Numerical aperture，简称NA)定义为[5,6]

NA=n0sinθ

(1)

若设空气的折射率为n0,纤芯的折射率为n1，包层的折射率为n2，根据几何光学的原理可以推出数值孔径的折射率表达式为

(2)

通常认为空气的折射率约等于1，所以式(1)和式(2)中的n0可以省略，也就是说光纤的数值孔径与光纤的直径无关，只与纤芯和包层的折射率有关.

1.2 光纤数值孔径的测量方法

理论上只要测得光纤的纤芯和包层的折射率，根据式(2)就可以准确得到光纤的数值孔径，但实际上折射率的测量比较麻烦，因此在实验教学中很少采用此方法.其实，光纤数值孔径的实验测量方法还是不少的[6-9]，但在实验教学中常采用的是远场光强法和远场光斑法，其实验光路示意图如图1所示. 这两种方法都是利用光路可逆的原则，利用光纤出射端的性质替代入射端的性质.

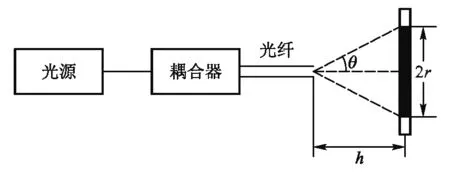
图1 远场光班法则试装置简图

远场光强法通过测量输出端光斑的光强分布，取光强下降到中心最大强度的5%处所对应的远场角度，计算光纤的数值孔径.

远场光斑法是通过测量远场光斑的直径，利用式(3)计算光纤的数值孔径. 如果想准确测量，通常还需要用已知数值孔径的光纤对测量系数进行修正[6].

(3)

本文重点不在如何准确测量数值孔径，而是主要研究影响光纤数值孔径测量的因素，因此没有采取修正的方法，而是直接采用远场光强法和光斑法的定义公式计算光纤的数值孔径，进行相对的比较.

2 数值孔径的实验测量

本文采用的测量光纤数值孔径的光路简图如图1所示. 首先用光纤专用切割器对光纤端面进行处理，在显微镜下观察端面，尽量选取端面平直与光滑的光纤，并将之固定在多维调节架上. He-Ne激光器经过显微物镜聚焦后入射到光纤端面，仔细调节光路的共轴以及光纤与光束的相对位置，直到获得足够强的输出功率，通常输出功率应大于100 μW，才能在接收屏上看到边界明显的光斑，本实验通常的耦合输出功率可以达到400～600 μW，光强较强，光斑明显.

在用远场光斑法测量NA时，先把坐标纸固定在光具座上作为观察屏，光斑打在其左侧(如图1)，坐标纸的刻度线向右，在观察屏右侧的一定距离之外放置手机并固定，用手机拍摄光斑，图像经放大后，测量光斑的直径，坐标纸的最小刻度是1 mm，所以光斑直径2r的大小可以精确到毫米量级. 光纤出射端到接收屏的距离用米尺(最小刻度为0.5 mm)或游标卡尺(最小刻度为0.02 mm)测量.

用远场光强法测量NA时，在光功率计前加一可调光阑，控制测量光强的范围，光阑的大小应小于测量光强时位置改变的步长，本实验中光阑的大小大约为1～2 mm. 将光功率计固定在可平移光具座上，移动方向垂直于光线传播方向，改变光功率计的位置，测量输出光斑横向的光强分布，然后作图测量光功率衰减到5%时对应的r，按式(3)计算数值孔径的大小.

3 实验结果分析

3.1 出射光斑形状对NA测量的影响

在实验中发现，由于耦合条件、光纤端面质量等因素的影响，光纤出射光斑的形状有很大的差异，如表1所示. 表1中的所有光斑是由同样的端面、同一根光纤通过改变光纤与光束间的夹角获得的，如果对端面进行不同的处理，还可以获得更加丰富的斑图形状，这主要是由于入射角度影响了光波在光纤中的传输模式.

表1 不同出射光斑对应的NA

表1中，编号由(a)到(c)，光纤与光束的夹角是逐步变小的，当光路共轴条件好的时候获得的是圆形光斑，如图(c)—(e). 此时若光纤拉紧绷直，稍微按压光纤，改变光纤的弯曲度，可以发现，光斑的中心可以由亮(图(d))变暗(图(c)),再变亮，呈现周期性变化，这表明出射光斑存在明显的衍射现象，其衍射特点与菲涅尔衍射类似. 当光纤弯曲度较大时，这种变化不再明显，但测得的输出光强明显减弱. 实验中，同样的耦合条件下，光纤绷直时输出光强为635 μW，而弯曲时只有330 μW. 这是因为本实验采用的光纤纤芯直径为9 μm，对于632.8 nm的氦氖激光波长来说，正处于强衍射尺寸区间. 而光纤弯曲导致损耗明显增大.

表1的NA是通过式(3)计算的，h的取值为120 mm左右. 很显然，如果光强足够强，入射角对NA的测量有影响，但差别不是很大，表1中NA的最大与最小值之间的差别小于10%. 当光斑不是圆形时，较难确定光斑半径，此时通常会多取几个方向求直径的平均.

本文采用的是G652型单模石英光纤跳线，康宁公司给出的该型号数值孔径是0.14，采用的测量方法是用波长为1310 nm的光波进行一维远场扫描并以光功率下降到1%处对应远场角计算NA[10]. 虽然本实验所用光纤不是该公司的产品，但对于同一型号的光纤来说，应该差别不大. 根据文献中[6]给出的数值孔径波长换算公式：NA(1310 nm) = (0.960～0.979)NA(633 nm),可知此型号光纤在632.8 nm波长处的数值孔径约为0.143～0.146，与表1中的测量结果非常接近，说明用远场光斑法测量数值孔径是可靠和可行的.

光斑强度弱的时候，相应的可视边界会收缩，光斑的直径测量结果会变小(如图(e))，导致NA偏小. 光纤的弯曲导致光束相位的变化，使得出射光斑图样的结构发生变化，当中心出现暗斑时，测量到的NA只有0.115(表1中(c)图)，明显偏小.

3.2 衍射级次对NA测量的影响

仔细调节光纤的耦合，使输出光强最大，为了能够看到高级次的衍射环，要适当缩短h的取值，本次实验采用的h大约为40 mm,适当增加手机的曝光时间，此时获得的光斑图像如图2所示. 此时可以明显看到第3级次极大衍射环，分别计算各衍射环对应的数值孔径，得到表2所示的数据.

图2 增加曝光时间后的衍射斑

表2 不同衍射级次对应的NA

由图2可知增加曝光时间后，光环的边界明显外移，测量得到的NA偏大，比如第1次极大对应的NA为0.163，比表1中的值大了13%，当然由于此时距离较小，也可能导致测量误差，后面将谈到测量距离对NA测量的影响.

在学生实验中，由于学生对实验技术的掌握不如老师熟悉，对光纤端面的处理和耦合光路的调节效果不佳，导致光纤耦合效率偏低，出射光斑强度不够，若再叠加环境亮度比较大，测量距离较远，此时学生在用肉眼判断光斑时，有时只能看到中心主极大，此时他测得的数值孔径就可能严重偏小(比如实验测量值为0.08)，这种情况在教学中时有发生.

3.3 h的取值对NA测量的影响

根据式(3)，观察屏与光纤的距离，对NA的测量时会产生影响的，本文在保持光纤耦合和输出条件不变的情况下，改变h的取值，测量了NA的变化，实验结果如图3所示.

图3 实验测得的NA值随h变化

由图3可知，当h取值较小和较大时，实验测得的NA值都偏小，究其原因，观察屏靠太近时，光斑太小，由于坐标纸的最小刻度为1 mm, 直径测量的相对误差变大，此时测量到的NA是可能偏大，也可能偏小.本次实验的结果是偏小为主.

而当屏太远时，光斑发散严重，边缘模糊不清，测得的半径偏小，这都会导致NA的测量值出现较大的误差. 由图3中可以看出，当h的取值在100～250 mm区间时，测量结果相差不大，这和大多数学生得到的结果相似. 教学中可以要求学生取3～5个距离进行测量，并分析距离对实验测量结果的影响，找到实验测量的优化条件，让学生学会分析问题、解决问题，而不是按部就班测量实验数据.

3.4 远场光强法测量NA

调节光功率计的横向位置，逐点测量光斑的光功率(记为P)分布，此时光纤出射端与光电探头的距离h设为10 cm左右，h的取值要根据光斑光强和光电探头的灵敏度进行选择，既要保证有足够的测量点， 又要保证实验点的光强测量值足够大.

图4中曲线b是表1中的c图的光功率分布曲线，而曲线a是表1中d图的光功率分布曲线，根据1.2节中远场光强法的定义，找到光功率由最大下降到5%时对应的位移，利用式(3)测量NA. 本文测得曲线b对应的数值孔径为0.0935，而曲线a对应的数值孔径仅为0.0621。由于衍射的存在，光斑功率分布下降很快，第1次极大的光强仅有中心主极大的2%左右. 这种方法测得的NA实际上与表2中的中心亮斑对应的NA类似.

图4 远场光强法测量结果. 曲线a和曲线b分别为表1中(d)图和(c)图的光功率分布

如果把光功率下降到1%处作为计算标准，并且把测量范围扩展到第1次极大，则光强法测得的表1中(d)图的NA为0.145，这与远场光斑法的测量NA=0.143很接近. 这也许就是厂家把测量范围放宽到1%的原因.(c)图用此方法修订后的NA变化不大，只略有增加.

4 结论

本文分别用远场光斑法和光强法测量了石英单模光纤的数值孔径. 实验结果表明，由光纤耦合条件不同导致的光斑形状变化，对数值孔径的测量影响不大，对非圆形光斑，测量其直径时应多方向测量求平均.由于单模光纤的纤芯只有9 μm，出射光存在较强的衍射现象，对数值孔径的测量造成较大的影响，无论采用光斑法还是光强法，需以衍射第1次极大为计算标准，这样测得的数值孔径更接近其实际值. 尽量选择光斑中心为亮斑时测量数值孔径. 此外，测量时观察屏到光纤的距离要合适，太短或太长都会导致实验误差的增加.

以前在教学中采用光斑法测量数值孔径时，通常让学生用肉眼判断光斑的边界，此方法受环境亮度、光斑亮度和观察距离的影响较大，导致测量结果差异较大，让学生觉得光斑法测量NA不靠谱，因此在今后的教学中，应多采用拍照法，利用照片分析并测量光斑直径，这会使得实验结果更加的稳定.

光纤数值孔径的测量可以促进学生应用光学知识解决实验问题，更好地理解光纤的工作原理，提高光学实验技巧，是值得在教学中关注的实验内容. 由于本实验的理论知识比较简单，在实验中应尽量让学生自主学习和研究，培养实验能力.