再谈“PT 对称的非厄米体系的能谱性质”
2021-04-27闫茂玉
闫茂玉,陈 兵
(山东科技大学 电子信息工程学院应用物理系,山东 青岛 266590)
众所周知, 量子力学的出发点是5个基本假设,即波函数公设、微观粒子动力学公设、算符公设、测量公设、全同粒子公设. 其中, 算符公设提出量子力学中的力学量必须用厄米算符表示, 这是因为厄米算符的本征值为实数, 是可观测量. 而且量子态在厄米哈密顿量中随时间的演化是幺正变换, 保证几率守恒律[1], 然而对于PT对称(宇称-时间反演对称)的非厄米系统也可以具有实数本征谱[2]. 文献[3]基于PT对称的一维紧束缚模型讨论了体系虚数势能对其能谱的影响, 但文章只讨论了偶数格点系统能谱变化的特点. 本文在文献[3]的基础上, 对PT 对称的非厄米体系的能谱性质重新进行了讨论.
1 PT对称的非厄米模型
为了文章的完整性, 我们从文献[3]建立的一维紧束缚模型出发重新进行问题的讨论. 系统的哈密顿量为
(1)
其中γ为虚数势的强度,t为相邻格点间的耦合强度的大小,N为系统格点的总数.
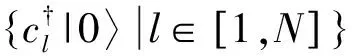
(3)
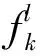
(4)
对应的本征值为
λk=-2tcosk
(5)
式中k=mπ/(N+1),m∈[1,N]表示系统的波矢.
下面讨论γ≠0时对系统能谱的影响. 设本征态的形式解为
(6)
将其代入哈密顿(1)的本征方程不难发现, 系统的本征值λk在形式上仍然保持式(5)的形式, 但波矢k则由下式确定
γ2sin [k(N-1)]+t2sin [k(N+1)]=0
(7)
2 PT对称系统能谱的讨论
如文献[2]所指出的,PT对称系统的能谱受虚数势γ的取值的影响. 主要表现为|γ|的取值存在临界值|γc|, 当|γ|<|γc|时系统的本征值存在N个纯实数解; 当γ=γc时系统的本征值出现合并; 当|γ|>|γc|时, 系统PT对称性出现破缺, 反映出来的结果是系统的本征值存在N-2个纯实数解,另外2个以共轭复数对的形式存在. 因此, 临界值|γc|是非厄米相变发生的临界点, 也称例外点. |γc|的取值与N的奇偶性有关:
(8)
接下来我们详细讨论当|γ|=|γc|=t时, 系统能谱的性质. 由于|γc|的取值与N奇偶性有关, 所以我们将分成两个方面分别进行讨论.
2.1 N为偶数
取|γ|=|γc|=t, 式(7)可简化为
sin (kN)cosk=0
(9)
不难得出方程的解为k=π/2或k=mπ/N,m∈[1,N-1]. 因为N为偶数, 所以当m=N/2时,系统存在两个完全相同的波矢:k=π/2. 该波矢值对应的本征态和本征值完全相同, 这一点与厄米系统所反映出来的性质有很大的不同(在厄米系统中,简并能级的本征态是正交的).
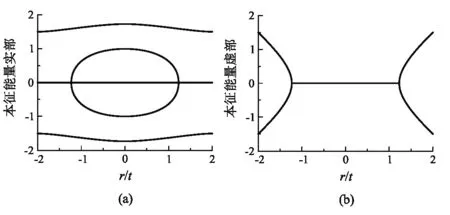
为了清楚的展示γ取值对能谱的影响, 图1展示了N= 4系统的本征能量与γ的函数关系, 其中图1(a)展示了本征值的实数部分, 图1(b) 展示了本征值的虚数部分. 可以发现, 当|γ| 本征能量的实数部分 本征能量的虚数部分图1 N=4系统的本征能量与虚数在位势γ的函数关系 Nsin (kN)cosk-cos (kN)sink=0 (10) 上式为超越方程, 波矢k没有明确的表达形式. 因为N为奇数, 不难发现k=π/2仍是方程(7)式的解, 此波矢对应能量为零的本征值. 图2展示了N=5系统的本征能量与γ的函数关系. 可以发现, 当系统处在精确PT对称相时, 5个本征值均为纯实数. 当系统处在PT对称破缺相时, 系统3个本征值为纯实数, 2个为纯虚数解; 在例外点, 系统有3个本征态出现合并. 这一点与N为偶数的情况有所不同, 其原因在于当N为奇数时始终存在一个与γ取值无关的能量为零的本征值. 通过对比图1和图2的结果我们发现,在该模型中无论格点数的奇偶,只有两个能级经历实数到虚数的转换. 图2 N=5系统的本征能量与虚数在位势γ的函数关系 本文在文献[3]的基础上详细讨论了PT对称的一维紧束缚系统中虚势对其能谱的影响, 补充了当系统维度为奇数时, 虚数在位势对能谱影响的讨论. 结果表明系统的能谱性质受虚数在位势的取值的影响: 当|γ|取值小于临界值|γc|时, 系统的本征值全部为实数解; 在例外点, 系统的本征值出现合并; 当|γ|取值大于|γc|时, 系统有两个能量本征值由实数转变为虚数, PT对称发生自发破缺. 此外, 临界值|γc|的取值还与系统维度的奇偶性有关, 在热力学极限下,N→∞,γc的取值将趋于一致. 上述现象出现的原因是γ的取值虽然不影响哈密顿量的PT对称性, 但会对哈密顿量本征态的PT对称性产生影响. 当|γ|取值小于临界值|γc|时, 系统的所有本征态都具有PT对称性, 此时所有的本征值为实数. 当|γ|取值大于临界值|γc|时, 部分本征态的PT对称性发生破缺(即该本征态不再具有PT对称性), 这些对称性破缺的本征态对应的本征值转变为纯虚数, 其余保持PT对称性的本征态对应的本征值仍为实数.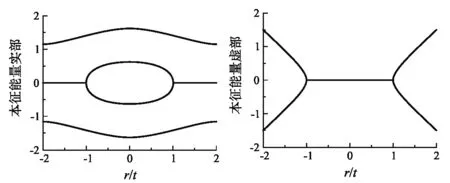
2.2 N为奇数

3 结论
