利用费曼路径积分理论分析多光子干涉

王瑞敏,刘丹东,徐忠锋

(西安交通大学 物理学院，陕西 西安 710049)

量子力学中，光子干涉是学习和理解光的波粒二象性的重要实验依据.同时，由于它在量子信息处理方面的应用潜力，也是目前量子光学研究的热点之一[1]. 狄拉克曾指出：每个光子只能和自己干涉，不同光子之间的干涉是不可能发生的.狄拉克的表述是对一阶干涉来说的，而双光子干涉是二阶干涉现象.对二阶干涉，乃至高阶干涉的解释，目前存在不同的理论[2].

量子力学有3种表述形式，波动力学、矩阵力学和费曼路径积分[3].目前国内的量子力学教材都在沿用波动力学和矩阵力学两种最早出现的表述形式，几乎没有介绍费曼路径积分理论的.因为, 多数人认为对所有路径求积分是将该理论引入教学的一个难点[4].然而，用费曼路径积分处理微观粒子的干涉，不用考虑狄拉克的表述，一阶和高阶干涉具有统一的理论解释[5].它使得经典力学和量子力学之间的过渡不再有任何困难.我们在教学中指导学生利用费曼路径积分理论，推导了双光子二阶干涉和三光子三阶干涉，让学生鉴赏到这种新方法的方便、直观.同时，帮助学生进一步理解量子干涉现象,也了解了目前量子力学的前沿发展.

1 两热光源的二阶时间干涉

双光子二阶干涉的理论和实验研究有很多研究报道[2,6]，包括非经典光源和热光源.我们首先介绍用费曼路径积分理论得到的二阶时间干涉的结果.图1是双光子干涉实验装置图.两个非简并的准热光源S1和S2，发出两个光子A和B.光子通过分束器BS后被两个单光子探测器D1和D2接收，并触发双光子符合计数系统. 实验中测量分束器输出端符合计数率，根据符合计数率的极值变化判断是否发生干涉. 对于时间干涉，我们规定两个光源到两探测器的距离r相同，并设两光源的强度相同，中心频率分别为ω1和ω2，频率带宽都为Δω. 对于多光子干涉，光源和路径的不可区分是产生干涉的关键.虽然中心频率不完全相同，但当时间测量的不确定度小于1/|ω1-ω2|时，可以认为是不可区分的[7]. 此时，就会出现干涉现象，干涉规律可以用二阶关联函数，即双光子波函数的模方表示. 对于所有可能的积分路径，我们可以通过列表法来直观展现.如表1，两个光子A和B可以由同一个光源S1或S2产生，也可以分别由不同光源产生，存在4种情况. 在每种情况下，两个光子到达两个探测器又存在两个不可区分的路径. 第1种是光子A到达探测器D1，B到达D2.第2种是光子A到达D2，B到达D1. 根据费曼路径积分叠加原理，总的概率波幅是所有可能路径的概率波幅之和.二阶关联函数Φ(2)(t1,t2)包含上述4种产生光子情况下对概率分布的贡献.

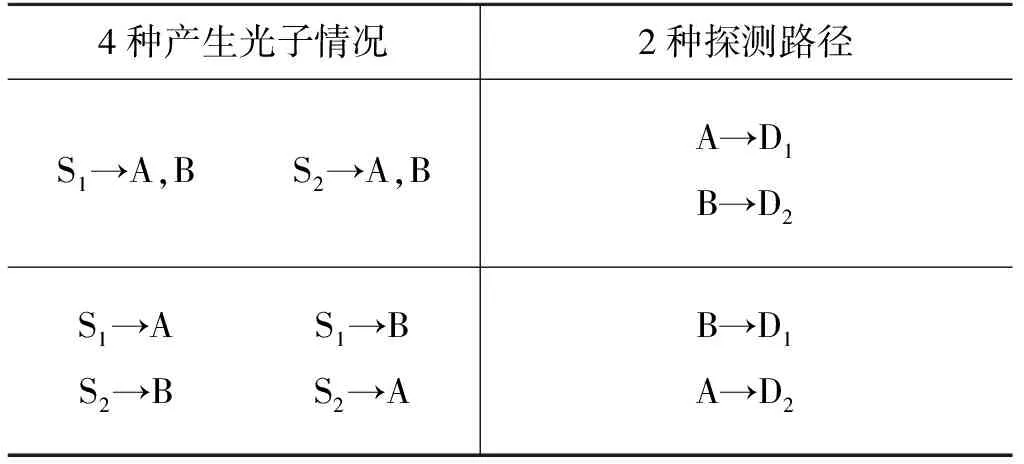
表1 二阶干涉光源和路径不可区分的各种情况

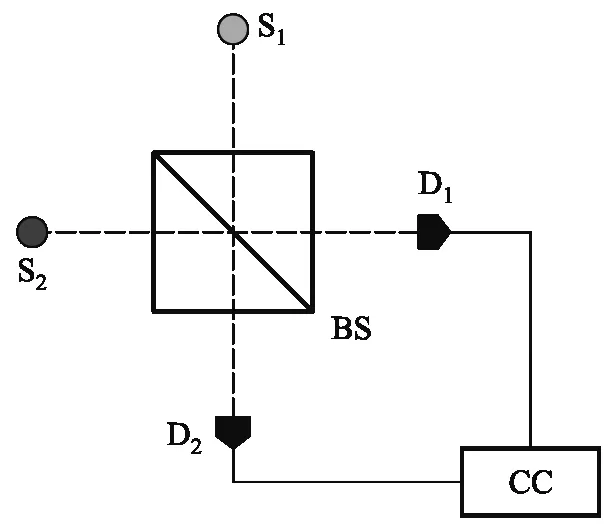
图1 双光子二阶干涉光路图

Φ(2)(t1,t2)=〈|Φ1j(t1,t2)+Φ2j(t1,t2)+

Φ3j(t1,t2)+Φ4j(t1,t2)|2〉

(1)

其中每一项又包含两个不同路径的贡献，等于两个路径的概率分布之和. 如第1项两光子都由光源S1发出，光子A到达探测器D1，B到达D2. 或者是光子A到达D2，B到达D1，则

(2)

第2项两光子都由光源S2发出时，

(3)

在这里，触发一次三光子符合计数的情况虽然多，但表现在公式里只是角标的轮换，其它项具有完全相同的形式，学生不难理解. 将费曼光传播算子(4)式代入后可得三阶关联函数

(4)

将其代入式(1)后可得

(5)

在现场作业工作完成后，要对现场进行仔细清理，并且注意要恢复现场的有关安全防护措施，还原原有的设备定置，防止由于作业而给现场留下日后的安全隐患。

2 两热光源的三阶时间干涉

{1+cos[(t1-t2)(ω1-ω2)]+

图2 三阶干涉光路图

表2 两光源三阶干涉的所有可能路径

(6)

每种产生光子的情况下，A、B、C三个光子到达3个探测器D1、D2、D3，又存在6种不可区分的路径(如表2所示). 因此，式中每一项又等于6种路径的概率幅之和，如

故宫解说词，作为一种旅游文本，集文学性、艺术性、宣传性为一体。其英译的目的是满足外籍游客的基本信息需求，并实现跨文化交际。在连贯性原则的指导下，故宫的英译文本应使用类似目的语的写作手法，提高语言的可读性，提供充分的背景信息帮助外籍游客更好地了解文物的文化内涵。而忠实法则要求译者要注重文本的内在逻辑，忠实于原文。

式中前3项代表两光子之间的二阶干涉，最后1项代表三光子之间的三阶干涉. 由此可见，三阶干涉包含二阶干涉的所有信息.

(7)

其它项有相同的形式，只是角标变化. 式中φi jA,B表示光子的初相位，当光子经BS反射时需要附加π/2的相位. 由于2个热源是相互独立的，式(1)中相位求统计平均后为零.Kαβ是光源Sα到探测器Dβ的费曼光传播算子，它反映光子从Sα到Dβ的概率波幅. 对于热光源

式中sinc(x)=sinx/x,sinc2[Δω(t1-t2)/2]表示光子聚束项，cos(t1-t2)(ω1-ω2)表示拍频项.当两个频率相近的光子发生量子干涉时，会出现拍的现象，称为量子拍.

如图2，在双光子二阶干涉的实验基础上，增加一个分束器将光分为3束. 其中BS1为1:2，BS2为1:1，以保证3个探测器接收的光强度相同. 光源到3个探测器的距离都为r. 3个探测器的光触发3光子符合计数系统. 此时光源发出3个光子存在8种不可区分的情况，如表2所示. A、B、C三个光子可能由同一个光源S1或S2产生，也可能光源S1产生两个，S2产生一个，或者S1产生一个，S2产生两个. 总的概率波幅是这8种情况的概率波幅之和.三阶关联函数等于8项相加

cos[(t2-t3)(ω1-ω2)]+cos[(t3-t1)(ω1-ω2)]}}

对所有患者开展肿瘤组织间碘-125放射性粒子植入术治疗。首先,为患者开展经皮穿刺植入法治疗。针对肝癌,颈部癌症,口腔癌,肾癌等患者,于局麻下采用放射性离子穿刺植入针开展手术。患者于CT定位下按照所需间距及粒子数经皮穿刺植入病灶内部,保证粒子纵横间距在1-2cm之间。针对食道癌患者,可根据患者食道病变长度和狭窄程度,选择合适的放射性离子食管覆膜支架,开展植入。方法与普通食管支架方法相同,植入放射性离子为碘-125离子。

(8)

目前,澳大利亚职前体育教师采取阶段性的教育实习方式,即各个阶段的教育实习并非连续整体的一个周期, 而是贯穿于本科的四年时间之中，使职前体育教师每年都有机会到合作的中小学进行专业体验。以悉尼大学体育教育专业为例，从大学第一年起，学院每学期都会安排学生到中小学进行实习(总共80天)，实习的时长将随着学生教学水平的提高而逐渐增加(表5)。

3 三热光源的三阶时间干涉

我们还可以进一步在图2中增加光源S3，中心频率为ω3， A、B、C三个光子由3个光源发出，就可以得到3热光源的三阶时间干涉.用同样的方法列表统计3个光源发出3个光子的所有可能情况，如表3所示，此时共存在27种光源不可区分的情况. 3热光源的三阶关联函数包含这27种情况下被探测到的3光子概率分布的贡献，即

表3 三光源三阶干涉中光源不可区分的各种情况

Φ(3)(t1,t2,t3)=〈|Φ1j(t1,t2,t3)+Φ2j(t1,t2,t3)+

…+Φ27j(t1,t2,t3)|2〉

(9)

每种情况下，A、B、C三个光子到达3个探测器D1、D2、D3仍然存在6种不可区分的路径，与表2中完全相同. 因此，上式中每一项概率分布表达式的形式与式(7)相同，是6项相加，只是做角标的变化. 将费曼光传播算子代入后就可得三光子三阶关联函数. 由此可见，从双光子的二阶干涉到三光子的三阶干涉，乃至更高阶的干涉，分析思路相同，具有完全统一的理论解释. 通过这种方法可以让学生接触到高阶光子干涉. 对于多个积分路径的难点，利用列表法更容易使学生理解. 随着干涉阶次增加，关联函数包含的项数增多，会变得比较复杂. 对于多光子干涉比较复杂的关联函数，我们可以利用计算机模拟来给学生直观地展现干涉结果.

根据不同的分类标准，研究方法有不同的分类方式。以研究的目标或目的为标准，可分为“基础研究”和“应用研究”；以研究方法为标准，可分为“定性研究”和“定量研究”；以研究方式为标准，可分为“理论研究”“实验研究”“调查研究”等。借鉴这些分类，本文将英语词汇学习研究方法分类两大类，一类是以实验为基础的实证研究，另一类是以理论分析为基础的理论研究。

4 干涉结果的模拟

图3是利用Mathematica软件对二阶和三阶时间干涉结果进行的理论模拟.在图3(a)双光子二阶干涉的结果中，可以看到在sinc2函数曲线的包络中存在很多干涉峰，它是光子聚束和拍频项共同作用的结果.图3(b)是三光子的三阶时间干涉的结果.可以看到，在中间主峰两侧出现了次峰，它是两光子和三光子聚束之间量子路径干涉的结果.我们可以说，多光子干涉是光子聚束和量子拍效应共同叠加的结果. 利用模拟结果可以让学生清楚地观察到多光子干涉和拍的现象. 图中改变频率和相对时间延迟，还可以得到更多干涉规律[8].

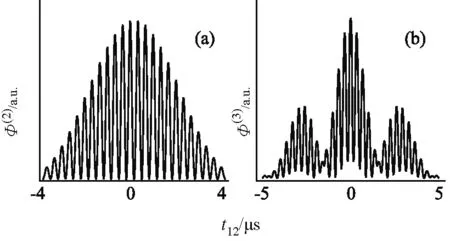
图3 (a)非简并双光子二阶干涉模拟， (b)非简并三光子三阶干涉模拟 (设定t3=0，t12=t1-t2为相对时间延迟)

5 总结

我们利用费曼路径积分理论推导了双光子和三光子干涉的关联函数，并且探讨了将费曼路径积分理论引入本科量子力学教学的可能性.费曼路径积分对一阶和高阶干涉具有统一的理论解释，利用这种方法可以让学生比较容易接触和理解高阶干涉.对于多个积分路径的难点，可以通过列表法来分析统计. 对于干涉结果，可以利用计算机模拟来直观展现.通过上述分析，使学生在其知识水平可以理解的范围内，对光子干涉和量子拍的现象有了深入的认识. 同时，也接触到了当前量子光学的前沿研究问题. 这是我们教学内容前沿性改革的一次尝试.