基于机器视觉的干涉条纹检测

王 叶，谢 雷

(1. 上海大学 理学院 物理系，上海 200444；2. 上海大学 通信与信息工程学院 通信工程系，上海 200444)

1 基本原理

1.1 机器视觉

机器视觉(Robot Vision)顾名思义就是视觉感知机器的意思，现在属于人工智能的一大技术发展方向，而某些计算机图像分析系统定义为计算机视觉(Computer Vision).霍恩[1]描述的机器视觉系统架构如图1所示.

图1 机器视觉系统架构

图1中的场景位于圆形光照区域内，成像仪器完成对场景的成像，机器视觉(软件部分)对图像进行理解和解释，这种理解和解释都是基于符号和算法程序的.

机器视觉的核心问题是：从一张或多张图像中生成一个符号描述，该描述显然和场景有关，并且包含完成指定任务所需的全部信息.

机器视觉的基本任务是：1)建立起对成像过程的基本理解；2)探讨对成像过程求逆的方法.具体实现时，机器视觉系统有专用和通用的(指提供一般化的二次开发环境)之分，当然还没有一个能够处理所有机器视觉问题的通用系统.

1.2 OpenMV

OpenMV是一种机器视觉系统，开发者的目标是要构建机器视觉的类似“Arduino”的开发环境，这种系统为用户和开发者提供友好简便的界面和封装对一般用户而言难度较大的算法.该系统自定义MicroPython语言并成为标准CPython实现的子集；硬件方面，系统基于STM32的嵌入式系统设计以及可扩充的外围和相应底层封装，最大限度内嵌软硬件一体化解决方案，这样就为用户提供了一个十分紧凑且通用的机器视觉开发平台或环境.

本文采用的实际系统为OpenMV4(STM32H7)，主频达480 MHz，板载的光学传感器(CMOS Camera VGA)型号是OV7725，最高帧速60 fps.

1.3 干涉条纹成像过程和特点

干涉条纹的成像不同于一般光照条件下的成像，尤其对于单纯的迈克耳孙干涉仪的干涉条纹成像，本文把这种成像称为“光源性”成像，原因在于成像过程及图像特征主要由光源特性(光波)，且为相干性决定，而将主要由非相干性的光强(照度)和场景变换决定的成像称为“光场性”成像.这里的干涉条纹“场景”可以理解为在光源性的“相干场”的作用下形成的“景”.机器视觉的任务就如下面的过程描述：基于光源的成像过程的基本理解→光学图像特性→图像形态特征→符号描述，图2给出了本文设计的干涉条纹机器视觉实现路线图.

图2 机器视觉实现路线图

干涉是光波动性的结果，时间相干性告诉我们，某一时刻两束光的叠加是两个有限长波列(或一个有限长波列的分振幅波列)的叠加，不同时刻的光波波列是随机的，即空间某个位置的叠加光波的相位差可以认为是恒定的，但是叠加幅度会有起伏，迈克耳孙干涉仪干涉条纹图像具有如下特点：

1) 在激光(如He-Ne激光)迈克耳孙干涉仪中，假设双点源球面波干涉的理想情况下(虚光源都位于中心轴上)，图像的形状特征为同心圆[2]，在一些情况下偏离为椭圆或其它形状[2,3]，以灰度图描述，指图像中的等灰度轨迹为圆或椭圆；

2) 由于干涉仪的“点源”成像特性，光源中心(源点)容易在干涉图像中心形成灰度饱和，干涉图像视场的中心坐标难以测定；

3) 由于共轴性偏离，在光程差变化时，干涉图像中心会发生漂移，即干涉条纹会发生整体漂移[4](或偏心)；

4) 条纹可见度存在起伏，主要原因为:扩展光束形成的光斑强度不均匀和不对称；光源的量子和相干特性增加了全局和局域性灰度噪声.

如果认为随机变量是遍历的，则对某处干涉强度采取统计平均是可行的(它们的强度是相关的，会影响相位精度)，相当于作低通滤波，然而可能最好的办法是使用中值滤波，它既能衰减随机噪声又不会使边界模糊，故这里采用3×3格子的中值滤波作为图像预处理，下面给出进一步的算法.

2 算法

2.1 灰度采样

如图3,设视场坐标系xOy，c代表以中心O为圆心的圆环(并不代表实际的干涉环)，在c上取P1、P2、P3和P44个坐标点，分别位于坐标轴上对称位置，设它们的图像灰度值为g1、g2、g3和g4，从P1、P2、P3和P4出发沿各自径向存在长度为ld的线段，命名为灰度采样线L.

图3 视场坐标系

定义与圆环c相关的灰度统计量为

[g1(x0+d,0)-g3(-x0-d,0)]2+

[g1(x0+d,0)-g4(0,-y0-d)]2+

[g2(0,y0+d)-g3(-x0-d,0)]2+

[g2(0,y0+d)-g4(0,-y0-d)]2+

[g3(-x0-d,0)-g4(0,-y0-d)]2}

(1)

(ld>0的偶数),为4个方向的灰度采样线中任意两条之间所有对应点之间的灰度差的平方和，在理想条件下，干涉条纹中心必和圆环c的中心重合，即位于视场原点上.若圆环c存在整体漂移，则c(i=0,j=0的情况)变为某个漂移位置cij(i、j不同时为零的情况)时的灰度统计量为

(2)

(Δg)ij=[g1(x0+i+d,j)-g2(i,y0+j+d)]2+

[g1(x0+i+d,j)-g3(-x0+i-d,j)]2+

[g1(x0+i+d,j)-g4(i,-y0+j-d)]2+

[g2(i,y0+j+d)-g3(-x0+i-d,j)]2+

[g2(i,y0+j+d)-g4(i,-y0+j-d)]2+

[g3(-x0+i-d,j)-g4(i,-y0+j-d)]2

(3)

在规定的漂移范围内的相似性判据为：(∑Δg)ij取最小值时所对应的圆环cij，此圆环可能已偏离视场中心.

又当存在纵向缩放时的表达式(干涉环发生椭圆化形变)为

(4)

(Δg)ijv=[g1(x0+i+d,j)-

g2(i,y0+j+d+v)]2+[g1(x0+i+d,j)-

g3(-x0+i-d,j)]2+[g1(x0+i+d,j)-

g4(i,-y0+j-d-v)]2+[g2(i,y0+j+d+v)-

g3(-x0+i-d,j)]2+[g2(i,y0+j+d+v)-

g4(i,-y0+j-d-v)]2+[g3(-x0+i-d,j)-

g4(i,-y0+j-d-v)]2

(5)

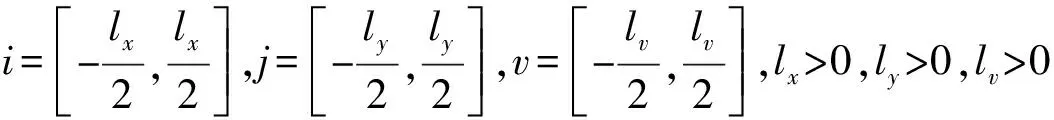
上述算法可以称为干涉条纹同心形态搜索算法，依据是基于灰度采样线的灰度统计量所给出的干涉条纹的形态相似性，此算法又是建立在“光源性”成像的干涉条纹特征及其动态变化基础之上的.为了计算方便，实际输出结果的描述为cij或cijv的外接矩形及其参数.

2.2 特征模板

定义4个灰度采样线形态特征模板T1—T4(用含有ld个元素的行向量表示)，分别表示灰度最大，灰度最小，灰度从大到小和灰度从小到大，后两者也称为等差向量，模板的大小可变，但是元素总数为大于1的奇数，模板定义如表1所示.灰度形态特征模板表示为

表1 灰度形态特征模板

Ti=[tij],i=1,2,3,4;j=1,2,…,ld

(6)

T1、T2灰度模板由每帧图像或有效区域的灰度最大值和灰度最小值构成其元素，T3、T4灰度模板由对灰度采样线进行灰度值重整得到，在灰度最大值和最小值之间进行均匀分割，模板T3线性减小，模板T4线性增加.

2.3 判据和规则

定义距离

(7)

lj是灰度采样线L的第j个元素，tij是Ti模板的第j个元素.匹配判据为(Dist.)i中最小的那个，即取最相似的模板Ti作为输出

To=Ti→minmun of(Dist.)i

(8)

由于存在4个方向的灰度采样线，实际计算时应对4条采样线上对应元素求平均值后再计算模板和距离.经连续采集两帧图像，根据两个输出模板的前后相互关系可以得到精度取决于帧速和条纹移动速度的冒出陷入的条纹合计总数(为正时表示冒出，为负时表示陷入，可以有小数，即条纹细分数).

当帧速vf和条纹移动速率vfr大约满足

(9)

可以用图4的模板变换关系确定干涉条纹的冒出和陷入的计数规则，精度为0.5个条纹，冒出加0.5，陷入减0.5.

图4 过极值点的条纹计数规则

3 实验

基于OpenMV4(STM32H7)，实验采用两种方案进行，首先是对仿真干涉条纹进行检测，图5为用Matlab 编制的一段仿真干涉条纹陷入的视频中的11帧画面(每隔20帧取一幅)，放映速度为每秒25帧，将摄像头对准电脑显示屏上播放的仿真干涉条纹并使部分中心级条纹位于视场区域，仿真干涉条纹存在可辨中心并易于和视场中心重合，而且仿真干涉条纹的视场亮度比较稳定且条纹不会发生漂移或抖动，本系统通过手机发送字符命令启动测量，测量所得环数和仿真条纹的陷入环数严格相符.接着进行真实的迈克尔逊干涉实验，OpenMV机器视觉集成开发环境和干涉条纹检测系统软件界面如图6所示(与仿真干涉条纹检测实验所用系统相同)，在抓图之前，程序关闭了自动增益和白平衡，并将对比度、亮度和饱和度设为合适值.从界面视频窗口观察到的干涉条纹中心确实处于饱和状态，但并不影响本算法的执行，实验方法和步骤如下：

图5 仿真干涉条纹

1) 按一般的激光迈克尔逊干涉仪调整步骤调整干涉条纹至圆环状态并大致位于毛玻璃屏中央；

2) 打开OpenMV机器视觉系统应用程序(图6)，连接设备(OpenMV4)后启动执行主程序，程序进入主循环后循环执行干涉条纹同心形态搜索算法.将摄像头对准干涉条纹所处毛玻璃显示屏，调整摄像头位置(也可以细微调整干涉条纹整体平移)使视场中的方框所代表的区域取在中心区域外可辨的第一个干涉环和第二个干涉环之间，方框的大小可以预先设置，摄像头和毛玻璃屏之间的距离和干涉条纹聚焦成像及大小也可以调整；

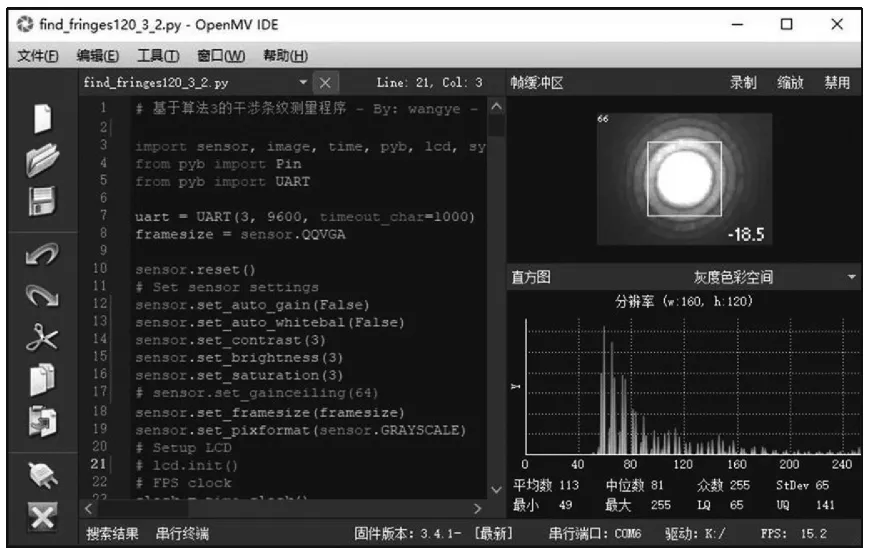
图6 OpenMV机器视觉集成开发环境及干涉条纹检测系统

3) 观察干涉条纹同心形态搜索算法的计算结果，即步骤2的调整过程可以将式(1)给出的(∑Δg)c值变为最小时作为调整到位的判据(灰度采样的相似性判据)；

4) 发送干涉条纹测量命令，程序进入环数测量子循环，此后有三种干涉条纹同心形态搜索算法可供选择运用，即式(1)的搜索算法对应于干涉条纹始终为圆且不发生漂移的情况，式(2)、(3)的搜索算法对应于干涉条纹始终为圆且发生微小漂移的情况，式(4)、(5)的搜索算法对应于干涉条纹发生微小漂移且存在纵向椭圆化的情况，如果干涉仪及机器视觉系统处于比较理想的状态，则干涉条纹整体在测量过程中始终保持圆环形状并且没有漂移，灰度采样线所在的圆环c(方框)固定不变，如果灰度采样线所在的圆环(方框)既发生漂移或又存在椭圆化(变成矩形框)，则图像的cij或cijv参数发生变化.每帧图像的基于灰度采样线的干涉条纹形态用形态特征模板Ti描述，比较相邻两帧图像的干涉条纹形态特征模板的变化即可得到干涉条纹动态变化情况.由于测量是自动进行的，只要干涉条纹发生冒出或陷入(相位差发生变化)，被检区域(方框附近)的干涉条纹形态就将发生变化，体现在极值处，冒出陷入的半环数以及总的环数将被检出.

软件界面视频窗口左上角的数据表示程序处理当前帧的用时为66 ms，右下角显示的FPS为帧速，当前为每秒15帧，它是处理时间的倒数.在式(9)的条件下实验测得陷入的干涉条纹总数为18.5个，和仿真干涉条纹检测相比，实际干涉条纹检测实验的整体光场强度和干涉条纹对比度随时间可能发生变化，由于程序采用连续帧的两个模板比较算法以及全域对称多采样线灰度统计算法，缓慢的光场强度变化以及对比度涨落就被上述算法抑制或平均掉了，另外手动测量会因为存在来回抖动等原因而产生计数误差，如果这种抖动发生在峰顶或谷底附近且速率低于帧速，则可能的过峰或过谷过程将被正常检测而不会遗漏，其它地方发生的抖动对当前精度下(0.5个条纹)的测量结果没有影响.

下面通过实验数据进一步说明测量的有效性以及进行误差分析.表2为实际手动测得的冒出和陷入50个条纹的数据，每隔5个条纹记录一次数据，为保证标称环数差Δk的准确性，采用录制视频后复播查数据的方式记录数据.

表2 干涉条纹测量数据

实验过程符合或作如下假设：各次测量Oi或Ii互不相关；Oi或Ii符合正态分布，方差相同；过极值点的条纹计数规则(图4)有效可靠或失效概率较低(如由极值点附近发生快速抖动导致漏检的概率较低，而过极值点来回抖动一次如果双向都漏检则不会产生影响).

从表2数据看出，条纹冒出过程的检测非常准确，条纹陷入过程的第2个记录和第1个记录之间出现漏检，接着记录数据保持准确，直到第9个记录和第8个记录之间又出现漏检，说明偶然出现的漏检将可能使数据发生整体偏移(数据2-8)，如果运用逐差法处理数据，将可能使这种整体偏移得到某种程度的校准，如设:

x1i=Oi+5-Oi,

x2i=Ii+5-Ii,i=1,…,5

(10)

采用所谓的简易算法计算A类不确定度，即将逐差后的结果x1i和x2i视为等精度测量值，则A类不确定度计算公式为

t0.95≈2.78

和

(11)

表3 数据处理

冒出25个条纹的检测结果：

x1=25.0±0.5(个)

(12)

陷入25个条纹的检测结果：

x2=-24.7±0.6(个)

(13)

显然，适当增加测量次数(环数)及选择合适的逐差间隔将提高测量可靠性和减小相对误差，对于干涉条纹相移型检测方法来说其实际的条纹检测精度(条纹细分度)一般不高(裸眼检测原则上有1个环的视觉误差)，因此产生的B类不确定度相对于A类数值上可能较大.

4 结束语

本文就干涉条纹检测技术提出了一种基于机器视觉的解决方案，发现研究过程对于光干涉及其干涉条纹有了更深的理解，技术上需要指出的是，本文只是基于OpenMV的软硬件一体化架构，运用其内嵌的一些基本的图像采集和处理函数结合MicroPython或Python语言来对自己提出的核心算法进行编程，主要考虑的是效率、鲁棒和实时性，从实现路线图来看，也可以采用其他方法，比如基于开源的OpenCV图像处理以及计算机视觉算法，组件自己的摄像头和嵌入式系统等，最后形成的都是某种意义上专用的干涉条纹检测系统.另一方面，从干涉条

纹检测技术的历史来看，此类干涉条纹的检测经历了从模拟方式(包括裸眼)到数字化[5-8]，从一维光电信号到二维图像处理的过程[9]，并且和现代光电子及通信技术进行了融合[10,11]，随着人工智能时代的到来，干涉条纹的检测技术会得到很大发展.