某水电站镶嵌式混凝土面板堆石坝渗流分析

杨专家，王开拓，施傅慧

(青海民族大学 土木与交通工程学院，西宁 810007)

我国很早就开始对水进行运用，古有李冰父子修建都江堰，今有三峡大坝等宏伟工程的建造。随着经济的不断发展，水源工程的数量日益增多[1]。据数据统计，我国目前大小水库约有80 000×104座[2]，其中大约有6.02×104座水库属于病险水库，数量如此之多[3]。这些病险水库对下游人民的生命安全形成隐藏的威胁，因此对水坝进行渗流分析和评价显得尤其重要[4]。本文选取青海省某水电站中一个镶嵌式混凝土面板堆石坝为例，研究坝体在稳定渗流场和非稳定渗流场情况下的变化规律[5-8]。

1 工程概述

该水电站于21世纪初正式建造，是一座以发电为主要目的的水利水电枢纽工程，工程规模为一等大(Ⅰ)型。该水电站坝型为镶嵌式混凝土面板堆石坝。其坝址正常蓄水位为2 715.0 m，死水位为2 710.0 m。水库调节库容为2.39×108m3，正常蓄水位时对应库容为14.724×108m3，死水位时对应库容为14.724×108m3[9]。水电站中有3台水轮发电机组，单机容量均为400 MW，多年平均发电量为47.406×104kW·h，其发电量可满足周边广大地区的用电需求。坝体由两部分组成，分别是混凝土面板堆石坝和嵌入底部的混凝土重力坝，坝体填筑总方量约为403.68×104m3。混凝土面板堆石坝坝顶长度为317 m，坝顶宽度为10 m，坝顶高程2 721.0 m，最大坝高150 m，上游坡比1∶1.4，下游第一级坡比为1∶1.4，其余坡比为1∶1.3，下游坝坡共设有8层10 m宽的上坝道路，综合坡比为1∶1.98。嵌入底部的混凝土重力坝坝高60 m，顶宽10 m，上游坡比为1∶0.2，下游坡比为1∶0.7，混凝土总方量为12.85×104m3。混凝土面板堆石坝坝体标准断面图见图1。

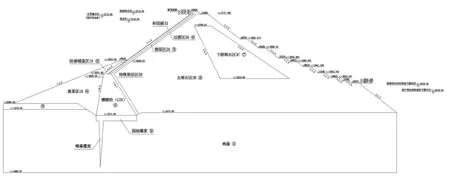
图1 混凝土面板堆石坝坝体标准断面(单位：m)

2 地质条件

水电站坝址区坐落于某峡谷段，该峡谷长约420 m，黄河以NE60°方向流入坝址区，流至峡谷出口成接近SN流向。黄河水面较宽，约为30～35 m，水深约为10～15 m，其枯水期水位为2 597.0 m。当达到正常正常蓄水位2 715.0时，谷宽为476 m。两岸在2 690.0～2 700.0 m高程处两岸发育基座阶地，阶面向上游抬高，略倾向岸外。在该高程以下，河谷呈现V字型，两边坡度较陡，平均坡度为53°～58°。在两岸坝基的基岩中，绝大部分是中厚层变质砂岩，只有少量区域为中薄层砂质板岩，其中砂岩所占比例较大，约为80%以上，与砂质板岩形成过渡相，但界限并不明显。河床坝基覆盖层较厚，厚度约为11 m，该覆盖层主要是由漂(块)石砂卵砾石构成，其结构松散，内部粗颗粒含量较多，级配不良，为强透水层。趾板基础中岩体完整性较好，主要以弱风化、微风化中厚层砂岩为主。

3 渗流稳定分析

3.1 有限元法

3.1.1 渗流有限元分析基本方程

公式如下：

(1)

式中：[K]为透水系数矩阵；{H}为总水头向量；[M]为单位储水量矩阵；{Q}为流量向量；t为时间。

3.1.2 非稳定流有限元基本方程

非稳定渗流计算的有限元方程与时间密切相关，通过对时间的控制与差分，可得如下方程：

(ωΔt[K]+[M]){H1}=Δt((1-ω){Q0}+ω{Q1})+([M]-(1-ω)Δt[K]){H0}

(2)

式中：Δt为时间增量；ω为0～1之间的一个系数；H1为时间增量结束时的水头值；H0为时间增量开始时的水头值；Q1为时间增量结束时的流量值；Q0为时间增量开始时的流量值。

取ω=0时，上述方程变为：

(Δt[K]+[M]){H1}=Δt{Q1}+[M]{H0}

(3)

在已知前一个时间步水头的前提下，按照式(2)递推，即可求得结果[10]。

3.2 稳定渗流分析

3.2.1 计算工况

本文采取3种不同的工况进行坝体稳定渗流计算，具体内容见表1。

表1 稳定渗流计算工况表

3.2.2 计算模型

为了更好地探究坝体在不同工况下的渗流规律、浸润线的位置及渗流量的大小，严格按照坝体分区设计，建立计算模型，见图2。

图2 稳定渗流计算模型

若计算无混凝土面板情况，应去掉土层定义中混凝土面板这一区域，再进行渗流计算。

3.2.3 计算结果

1) 无混凝土面板情况。见图3-图4。

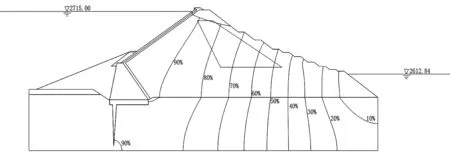
图3 正常蓄水位(设计洪水位)下准流网图(无混凝土面板)

图4 校核洪水位下准流网图(无混凝土面板)

2) 有混凝土面板情况。见图5-图6。

图5 正常蓄水位(设计洪水位)下准流网图(有混凝土面板)

图6 校核洪水位下准流网图(有混凝土面板)

通过图3-图6可以看出，图5、图6中浸润线的分布较复杂，且图3、图4中浸润线的位置高于图5、图6中浸润线的位置，现象较明显。故可得出，在正常蓄水位(设计洪水位)和校核洪水位两种不同的情况下，有混凝土面板的坝体浸润线位置明显低于无混凝土面板的坝体，可见混凝土面板对降低渗透有显著的效果。随着坝体浸润线的降低，坝体内含水土层减少，对上下游坝坡的稳定起到重要的作用。

3.2.4 稳定渗流综合分析

渗流计算结果见表2。

表2 渗流计算分析表 /m3·d-1

3.3 非稳定渗流分析

3.3.1 计算工况

本文只研究无面板情况，在此基础上，探究该水电站上游库水位从正常蓄水位2 715.00 m下降至死水位2 710.00 m时，库水位下降速度与坝体内浸润线的关系曲线。为了增强准确性，本文采取4种不同方案进行对比研究，具体方案见表3。

表3 非稳定渗流计算方案 /m·d-1

基于水位下降量相同的原则下，4种方案采用不同的时间间隔。方案一中以0.25 d为一个间隔，方案二中以0.5 d为一个间隔，方案三中以1 d为一个间隔，方案四中以10 d为一个间隔，选取不同的数据进行分析，不同方案下水电站下降水位与时间的变化关系图见图7、图8。

图7 前3种方案下降水位与时间变化曲线图

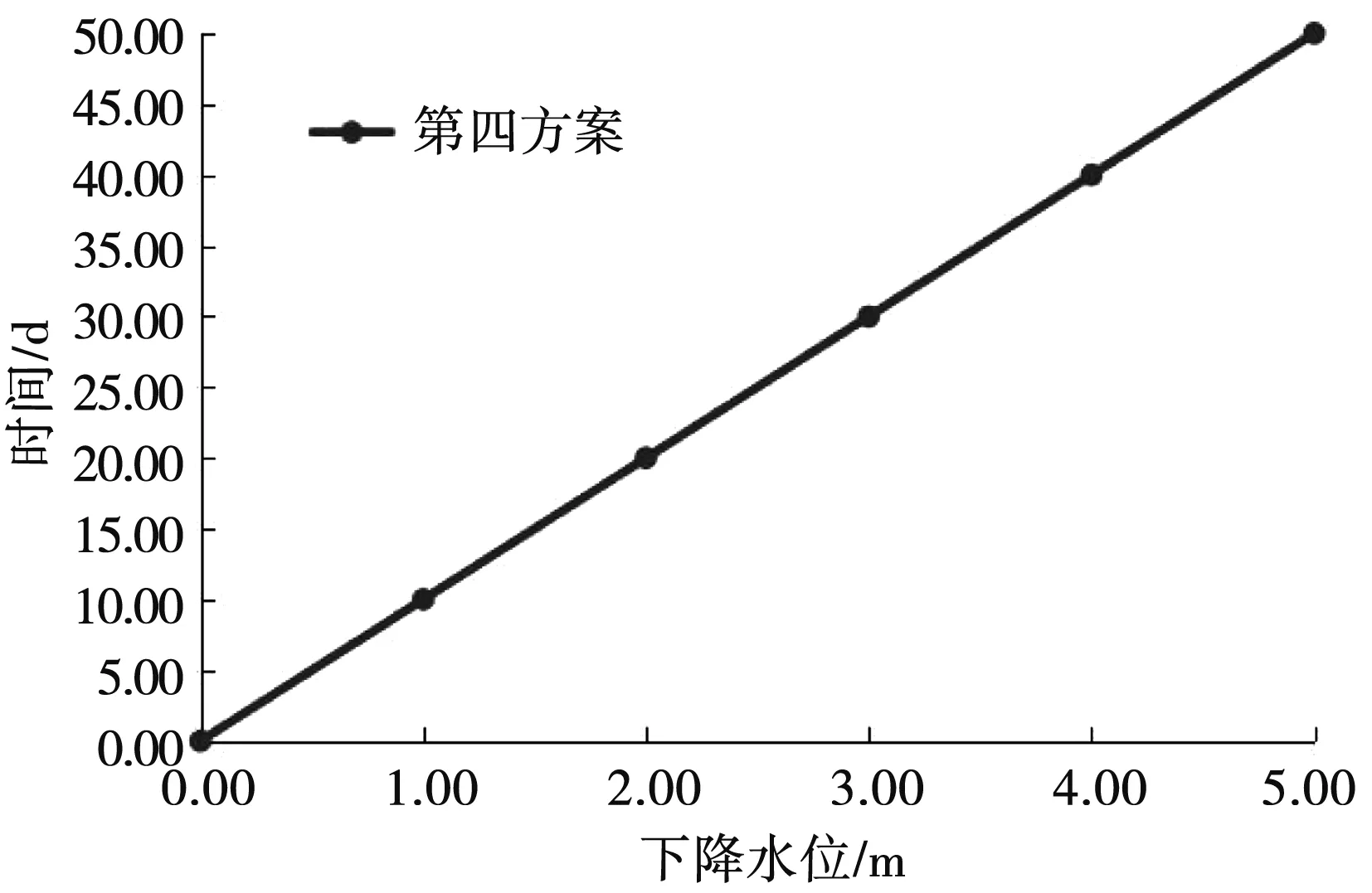
图8 第四种方案下降水位与时间变化曲线图

3.3.2 计算模型

非稳定渗流的条件下，其计算模型见图9。

图9 非稳定渗流计算模型

3.3.3 准流网图

3.3.3.1 稳态期

归化与异化，是根据译者不同的文化立场而呈现出的两种翻译策略。归化采取目的语所习惯的表达方式来传达原文的内容，当源语中出现目的语中的文化盲点或是有文化差异时，要用跨文化的词语来转换成读者熟悉的文化形象，便于目的语读者理解，避免引起误解。而异化，则尽可能地在翻译时迁就外来文化的语言特点，保留译出语的语言和文化差异，其目的是开拓译出语的文化形象色彩，在风格和其他方面突出原文本之“异”[3]，多采用源语的表达方式。

在稳态期间，4种方案下的准流网图均相同，具体图形见图10。

图10 稳态准流网图

3.3.3.2 水位下降期

1) 第一方案：见图11-图12。

图11 水位下降0.5 d的准流网图

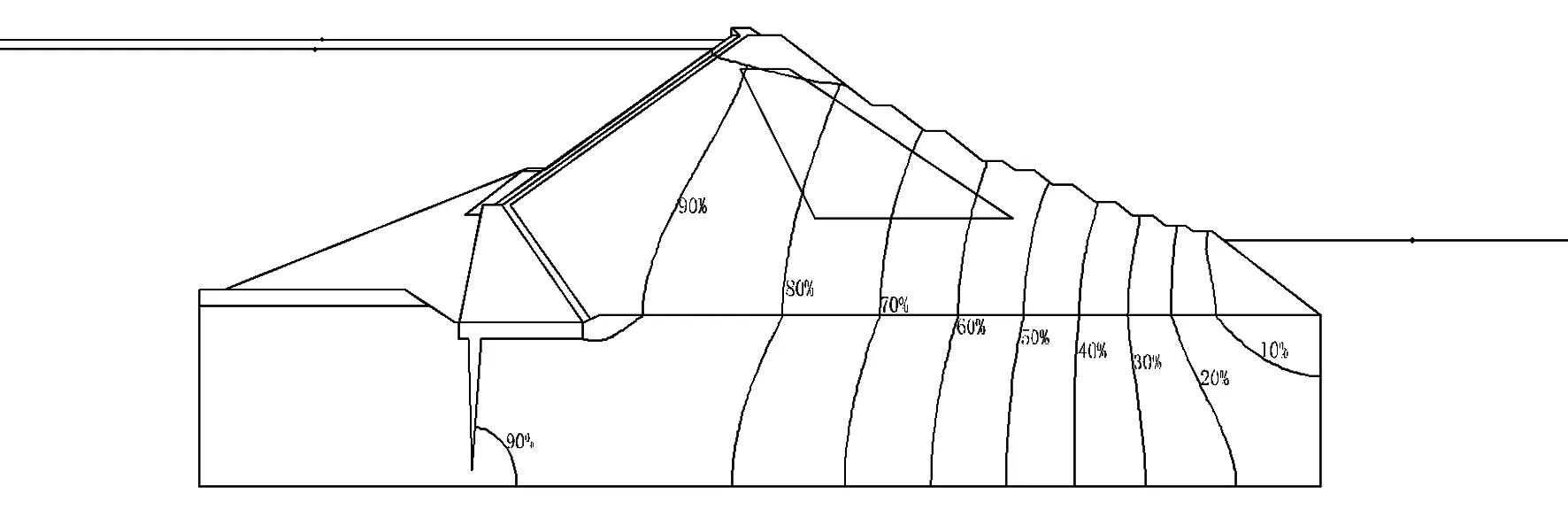
图12 水位下降1.0 d后准流网图

2) 第二方案：见图13-图14。

图13 水位下降1.0 d后准流网图

图14 水位下降2 d后准流网图

3) 第三方案：见图15-图16。

图15 水位下降2 d后准流网图

图16 水位下降4 d后准流网图

4)第四方案：见图17-图18。

图17 水位下降20d后准流网图

图18 水位下降40d后准流网

图11-图12、图13-图14、图15-图16、图17-图18分别反映4种方案下流网图的变化。图中仅画出一条流线即浸润线，用等势线的变化反映流线的变化。故可得，浸润线随时间逐渐下降，且土壤饱和度从上游至下游分别为90%、80%、70%、…、30%、20%和10%，呈现减小趋势。

3.3.3.3. 水位下降稳定期

见图19-图22。

图19-图22反映了不同方案下，水位降至死水位且稳定部分天数后准流网图的变化情况。从图19-图22中可以看出在方案一、方案二、方案三条件下，水位稳定部分天数后的准流网图差异不大。在方案四的条件下，从图22中可以得知，90%的占取比例增大。故可得出，当水位下降速度相差较大时，对准流网图也会产生一定的影响。

图19 水位稳定0.625 d后准流网图(方案一)

图20 水位稳定1.25 d后准流网图(方案二)

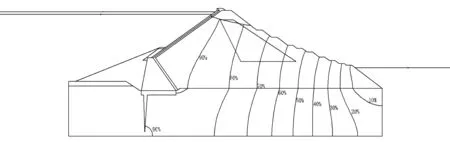
图21 水位稳定2.5 d后准流网图(方案三)

图22 水位稳定25 d后准流网图(方案四)

3.3.4 各时间步的浸润线变化情况

见图23-图26。

图23 各时间步浸润线变化图(方案一)

图24 各时间步浸润线变化图(方案二)

图25 各时间步浸润线变化图(方案三)

图26 各时间步浸润线变化图(方案四)

图23-图26集中反映了4种方案下，水位降落过程中浸润线的变化趋势。图23-图26中均反映出浸润线的位置一直在下降直至趋于稳定，即浸润线起点从正常蓄水位(2 715.00 m)下降至死水位(2 710.00 m)。

3.3.5 非稳定渗流综合分析

不同方案下浸润线最高点坐标变化值见表4，各时间步渗流量见表5。

表4 不同方案浸润线最高点坐标变化值

表5 不同方案各时间步渗流量表

从图11-图18即4种方案下的准流网图可以看出，随着水位的不断降低，坝体内降浸润线的起点也随之有所变化。结合不同方案下各时间步的浸润线变化情况，从图23-图26中可以反映出，当该坝体库水位从正常蓄水位不断下降直至到达死水位时，其浸润线起点的变化趋势均为一直下降直至趋于稳定。同时还可以观察出，图23中浸润线的下降速度明显高于图24、图25、图26中浸润线的下降速度，图24中浸润线的下降速度又高于图25、图26中浸润线的下降速度。故可得出，坝体浸润线的位置受库水位的影响，随着库水位的降低而下降，且降落位置的快慢又与库水位骤降速度密切相关。当库水位骤降速度较快时，坝体浸润线位置降落的速度也增加；当库水位骤降速度较慢时，坝体浸润线位置降落的速度也随之减小，但最终都将趋于稳定状态。表5反映了两种方案下各时间步渗流量的变化，由表5并结合表4可得，在总水头从正常蓄水位水头127 m开始降落至死水位122 m的过程中，该坝体总渗流量一直减小直至趋于稳定。

4 结 论

本文从渗流分析原理出发，以青海省某水电站镶嵌式混凝土面板堆石坝为研究对象，运用有限元方法进行稳定渗流分析，得出混凝土面板对坝体防渗的重要性，以及水位越高、浸润线位置越高、渗流量越大的结论。在稳定渗流计算基础上，进一步研究非稳定渗流，通过4种方案下的准流网图和各时间步浸润线变化图，得出坝体浸润线的位置与库水位有关。随着库水位的下降而降低，且降落快慢与库水位骤降速度成正比，但最终浸润线变化会趋于稳定状态。