基于ANSYS-LSDYNA联合计算的冲击体作用闸门时动力响应特征分析研究

程天竞，魏金亮

(1.淮安市水利工程建设管理服务中心，江苏 淮安 223300， 2.上海同瑞环保工程有限公司，上海 200040)

1 概 述

供水工程等水利工程中常用到闸门这类水工结构，针对该类水工结构，已有一些学者进行过静力稳定性分析或强度等校验设计工作[1-3]。但不可忽视，当流水中出现流冰体固体结构，其冲击碰撞作用会对闸门的安全稳定性带来较大影响，这类动力响应问题已不能照搬静力分析方法[4-6]。许多学者与水利工程师通过在室内进行修建水利工程等模型，基于试验研究水工闸门在冲击等动力荷载下结构响应特征，为闸门进行水工设计提供试验依据[7-9]。另外还可以利用现场安装传感器监测手段，研究闸门运营过程中数据变化规律，为评判闸门的安全稳定性提供参考[10-11]。作为工程领域重要研究手段，数值计算较为高效，能模拟计算出复杂工况中工程结构应力或位移等结果[12-14]，为水利工程设计提供重要的计算参考。

2 研究对象

某供水工程位于华北地区，承担着区域内水资源蓄水调度的重要作用，布设有6台泵机引水，蓄水池联通引水与输水管道，其中在蓄水池中前后端均设置有弧型钢闸门，准确调度水资源流量。供水工程设计资料表明，该闸门半径10 m，厚度2 m，以横纵梁支座作为骨架支撑结构，每个横梁高度1.2 m，宽约0.8 m，所用材料为22 mm的工字钢，共有13根横梁；每根纵梁高度为0.2 m，厚度约为12 mm，设置有加筋肋板，提升支撑结构抗弯性能，共有7根纵梁；支杆结构亦为工字钢，截面宽度为0.08 m，高为0.14 m，支杆连接臂为矩形梁体结构，整个支杆系统与横纵梁骨架结构之间以厚25 mm的隔板连接。弧形闸门设置有自动启闭机，启闭系统为液压控制，与引水泵机位于同一控制系统中，方便调度水资源。由于工程场地冬季气温较为寒冷，常常在引水过程中，在池内会形成浮冰，冰体一定程度上随流体作用，在闸门处产生一定的冲击作用，影响闸门安全运营。

根据现场调查发现，该供水工程所在场地无活跃地质构造，地势平坦，地层岩性主要分为3层：第一层为第四系人工活动堆积土层，主要包括有一些杂土及建筑材料碎屑等，密实性较差，分布在工程场地周围；第二层包括有粉质砂土，夹有淤泥，含水量约为29%，析水性较强，砂砾粒径基本均在6 mm以下，属细砂；另一层为粉质壤土，属基岩层上覆盖土层，密实性较好，取样表明土体局部处于软塑状态，厚度为3.6～6.8 m。基岩层为白云质灰岩，表面孔隙较少，完整性较好，承载力较强。本文将基于上述工程资料，开展分析流冰运动作用下弧形闸门的动力响应特征。

3 模态分析方程及建模

3.1 模态方程

在动力分析理论中，常常借助有限元离散概念，将复杂的弧型钢闸门进行离散化，转换成具有多个变形自由度体系的几何多边形结构。该结构的运动方程可用下式矩阵形式表述：

[M0]{x″}+[C0]{x′}+[K0]{x}={P(t)}

(1)

式中：[M0]、[C0]、[K0]分别为以矩阵形式表示研究体的动力特征参数；{P(t)}为外荷载；{x}为位移矩阵。

在水流中的闸门面对流冰的冲击荷载作用下，闸门与水流实质上是处于流固耦合状态。本文将利用附加质量法来进行模拟分析，其中水流作用遵循以下Laplace微分方程式：

(2)

将边界条件转化为泛函数或形函数的表达形式，代入运动微分方程中，获得有限元离散后的几何结构求解方程为：

[K]{δ}+[C]{δ′}+([M]+[Mp]){δ″}=[R0]

(3)

由式(3)可知，在无限制条件下的自由运动方程可表述为：

(4)

在上式基础上，离散化的几何结构冲击荷载下的振动方程为：

{δ}={φ}cosωt

(5)

式中：{δ}为振幅位移矩阵；ω为系统振幅位移变化频率。

联立式(3)、式(4)、式(5)，可得到振动的齐次方程为：

(6)

式中：ωi为研究体第i个自由度下的自振频率解；{φi}为第i个自由度的振幅位移。

通过有限元多次迭代求解计算，可获得弧型钢闸门离散化后的几何结构的应力、位移以及振动能量等。其中，能量与几何结构的自振频率有关，其频率微分方程表达式为：

(7)

3.2 建 模

利用HYPERMESH建模软件，基于工程实际资料建立弧形闸门几何模型，利用SHELL163作为微单元体，表现闸门在冲击荷载作用下具有弯曲变形能力，且该类单元体材料具有多达12个变形自由度，可充分模拟反映闸门在流冰体冲击荷载作用下振动位移及应力场特征，所建立闸门平面几何结构及赋予多面体单元结构后的数值模型见图1，所采用的SHELL62壳体单元几何模型见图2。另外，弧形闸门的支撑结构采用BEAM161单元体模型，其支臂结构建模后见图3。流冰体冲击荷载作用下对固体材料具有较强的拉伸应力塑性破坏，而流冰体自身亦会收到塑性变形失效破坏，故而本文流冰体模拟采用各向同性弹性变形下的断裂单元体模型。

图1 闸门数值模型图

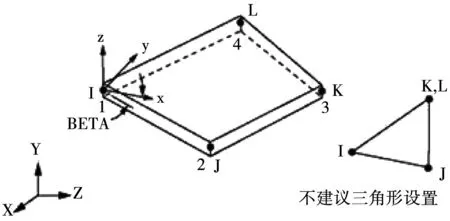
图2 SHELL62壳体单元几何模型

图3 支臂结构建模

当各部分结构均采用合适模型进行模拟后，以界面接触组合各个结构单元体，边界约束荷载施加在支臂的铰接点，只余下Z向变形自由度，外荷载条件包括有流冰体的质量与冲击速度。本文为体现动荷载特征，以冲击速度作为外荷载施加条件，其中速度参数为2 m/s，流冰体尺寸设计为长×宽×高=100 cm×100 cm×50 cm。基于上述动力特征理论与建模分析，在LSDYNA后处理软件中获得最终闸门动力特征。

4 冲击过程动力特征分析

4.1 能量特征

图4为流冰体模拟冲击弧形闸门时各能量特征参数演化曲线。从图4中可看出，由于本文所计算模型理论均是以能量守恒定律为基础推导出来的，故总能量特征曲线在冲击荷载持续时间线上，持续为水平线，即维持不变状态，为900 J。在其他能量特征参数中，以动能参数水平为最高，其变化曲线分为3部分。0～13.5 ms，该时间段内动能为0，闸门处于静止状态；从13.5～16 ms时间段内，动能从水平状态下降至最低点，下降幅度为61.1%，动能最低时仅为350 J；16 ms直至模拟试验结束时，该区段内动能上升至稳定水平，且动能长期维持水平在550 J上下，其中从最低点动能值上升至稳定状态时仅用4 ms，增大幅度达57.1%。另一方面，内能变化与动能波动趋势呈相反，动能下降时段，内能上升，甚至在初始冲击瞬间，短短2.5 ms内上升至550 J，后随动能上升，内能下降至稳定状态，持续维持在350 J上下。分析表明，动能与内能的3个变化段对应着流冰体冲击荷载对闸门作用，首先是流冰体与闸门之间处于远距离状态，还未碰撞接触，此区段内动能内能均为0；当流冰体冲击到弧形闸门后，动能逐渐从最高下降至最低，内能逐渐上升至最高；碰撞接触后，动能与内能逐渐保持在稳定状态。最后一个能量参数为滑移界面能量，体现了闸门各部分结构之间接触面上能量变化曲线，从图中可知滑移界面能基本为0，即闸门各部分结构接触面上不存在能量停滞，而是完整传递。

为比较冲击荷载过程中闸门各部分结构能量特征，给出图5所示结果。从图5中可知，最高能量值为挡水面板系统，其能量值长期稳定在475 J上下；能量最低为支杆系统，其能量在波动变化过程中最大值为前者的2.6%，仅为12.5 J；其中流冰体能量变化幅度最大，其从最高能量900 J在碰撞后，持续保持在350 J；还有横纵梁结构能量维持在45 J左右。从各部分结构能量变化曲线可知，闸门所受冲击荷载作用下，能量传递在挡水面板系统与横纵梁结构中发生，后传递至支杆等系统，故而冲击荷载下挡水面板系统产生较严重破坏，其次即为横纵梁骨架结构，因而在进行水利工程闸门设计时应考虑此方面。

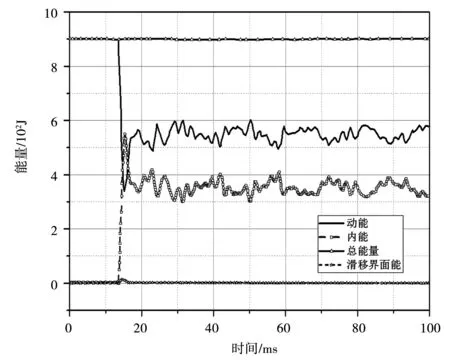
图4 冲击荷载作用过程闸门各能量特征参数演变

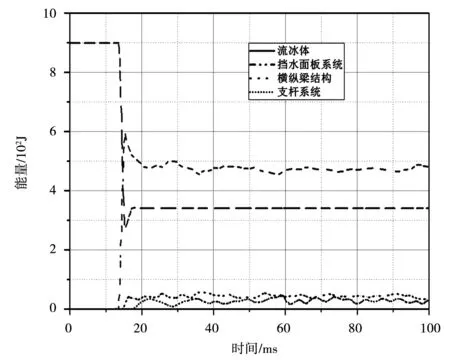
图5 闸门内部各组成结构系统能量演化

4.2 流冰体动力特征

为分析冲击过程中流冰体动力特征，得到图6所示的流冰体应力分布云图。从图6中可看出，在碰撞瞬间，第14 ms时最大等效应力为5.31 MPa，位于流冰体边缘区域；从流冰整体等效应力分布亦可看出，从边缘至流冰体内部，等效应力值逐渐减小，且最大等效应力发生在迎面闸门的边缘处，最小等效应力相比最大应力值少了近2个量级。在第14.5 ms时，最大等效应力相比第14 ms增长34.7%，达到7.15 MPa，其等效应力分布基本与前一时刻一致。在碰撞时间第15 ms时，流冰体最大等效应力相比第14 ms增长67.6%，达到碰撞瞬间中最高等效应力，为8.29 MPa。但在第15.5 ms时，最大等效应力相比碰撞瞬间的峰值等效应力下降12.9%；在第16 ms与16.5 ms时，最大等效应力分别下降33.4%和54.9%，即流冰体与闸门碰撞时最大等效应力呈先增后减变化，峰值出现在第15 ms，达到8.29 MPa，应力分布形态由闸门的迎面流冰边缘处逐渐递减至冰体内部后边缘。

图6 冲击荷载过程流冰体等效应力分布云图

4.3 闸门动力响应特征

针对闸门动力响应特征，本文以闸门上特征点位移为例开展分析。其中，所选取闸门特征点见图7，图7上编号为该特征点所在网格单元号。

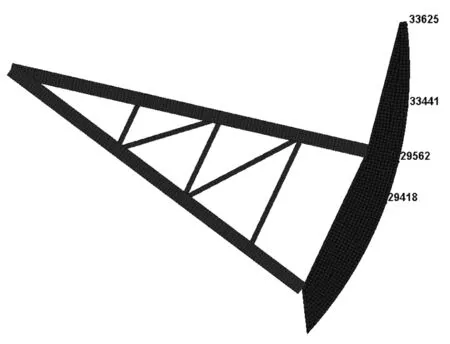
图7 闸门特征点

根据动力求解后处理，获得闸门上各特征点冲击荷载作用下位移变化(图8)。从图8中可看出，X向位移中各个特征点变化趋势基本一致，即呈先减小后上升再缓降，最后再抬升，最终各特征点均达到静止状态(位移为0)。从变化时间段来看，X向位移在前25 ms内变化有所紊乱，但从25 ms以后，各特征点位移基本变化趋势为一致性，即使波动变化，亦维持在位移为0上下。另各点X向振动位移幅度基本在-0.05～0.05 m范围内，其中以特征点D变化幅度最为显著，其最大位移达到0.075 m；最小位移为特征点A，达负向位移0.205 m。从Y向位移变化特征来看，在第16 ms后，整体上各特征点以正弦函数曲线形式变化，振幅为0.02 m，周期约为30 ms；第16 ms前，各特征点Y向位移中以A点变化紊乱，其最大位移达到0.07 m，后在第20 ms下降至0.02 m，从图7可知，A点为面板中间点，即冲击荷载作用下，闸门面板上以中间点Y向位移变化幅度最大，愈靠近面板边缘，其Y向位移振动变化愈趋近于正弦函数曲线变化。

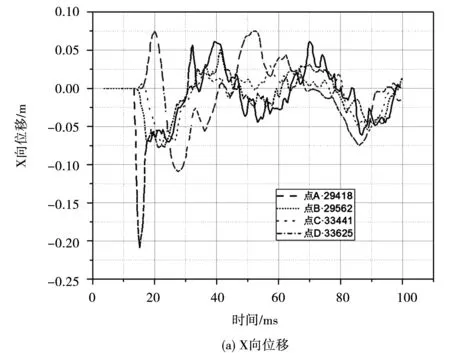
图8 闸门上各特征点位移变化曲线

5 结 论

1) 研究了冲击荷载作用下闸门能量特征参数演化规律，总能量持续维持在900 J，动能先不变，在第13.5 ms开始下降至最小值，达350 J，后逐渐上升；内能变化与动能呈相反态势，冲击碰撞后持续维持在350 J上下；滑移界面能基本为0；闸门系统中能量传递首先在挡水面板系统与横纵梁结构中发生，后发展至支臂等结构。

2) 获得了流冰体冲击碰撞瞬间最大等效应力呈先增后减变化，峰值出现在第15 ms，达到8.29 MPa；在第16和16.5 ms时，最大等效应力分别下降33.4%和54.9%，应力分布形态由闸门的迎面流冰边缘处逐渐递减至内部后边缘。

3) 分析了闸门冲击荷载下位移响应特征，X向位移在第25 ms后各特征点变化趋势基本一致，呈先减小后上升再缓降，最终抬升至位移为0，且波动变化幅度为-0.05～0.05 m范围；Y向位移在第16 ms后呈正弦曲线变化形式，振幅0.02 m，周期30 ms，闸门面板中部位移变化幅度最大，愈在面板边缘，愈为正弦波动变化。