基于响应面模型的注塑件精密成型工艺优化
2021-04-27傅建钢
傅建钢
(绍兴职业技术学院 机电工程与交通学院,浙江 绍兴 312000)
塑件质量决定了其制品的使用性能。塑件质量的优化通常从优化产品结构、优化模具结构和优化产品成型工艺等方面展开[1-3]。当产品结构和模具结构确定后,提高产品品质的途径就是优化成型工艺。目前,众多学者对产品成型工艺优化进行了研究。陈巍等[4]采用Kriging模型与自适应粒子群算法对注塑产品进行翘曲优化,以小样本获得较高求解精度。程锦等[5]采用变粒度策略处理注塑模流道的多目标优化设计问题,得到了不同粒度下的流道Pareto最优解。王梦寒等[6]将Kriging模型和GA方法相结合,研究了双层变模温注塑成型收缩控制策略问题,得到了最佳指标及其变量组合。姚文龙等[7]采用Taguchi试验设计,建立响应面模型,获得最佳工艺组合。
响应面法可有效解决正交试验法只能在实验范围内间断取点的问题,该法以样本数据为基础建立拟合函数,得到的结果更精确。响应面法需要大量样本点,但样本点过多则会导致计算时间过长。在保证较高的拟合精度的情况下,选择较少的样本点进行分析成为响应面法顺利实施的关键。在常见的响应面法研究中,Box-Behnken设计(BBD)和中心复合试验设计(CCD)是最常用的样本点选择方法。其中,CCD方法是较理想的样本点选择方法,较BBD方法能更好地拟合曲面。本工作运用CCD方法确定实验样本点,依次计算得到各实验组合下的体积收缩率,构建响应面模型,运用Design Expert数据分析工具寻找产品品质最佳的最优工艺参数组合。
1 注塑工艺优化试验设计
1.1 实验模型建立
注塑件为带螺纹瓶盖,厚度为2 mm,采用一模四腔形式布局,具有一定的生产效率。浇注系统采用平衡式进浇,保证熔体能够均匀填充。在产品上下两侧分别设置冷却水路,构成冷却系统。产品、浇注系统和冷却系统的有限元分析模型如图1a所示,最终完成的带螺纹瓶盖的注塑模具外形结构如图1b所示。根据实际使用需要,注塑件材料选用BP Chmicals公司的聚丙烯BP Amoco 4018,该材料的有关性能参数见表1。

图1 有限元模型及产品模具结构Fig.1 Finite element model and product mold structure
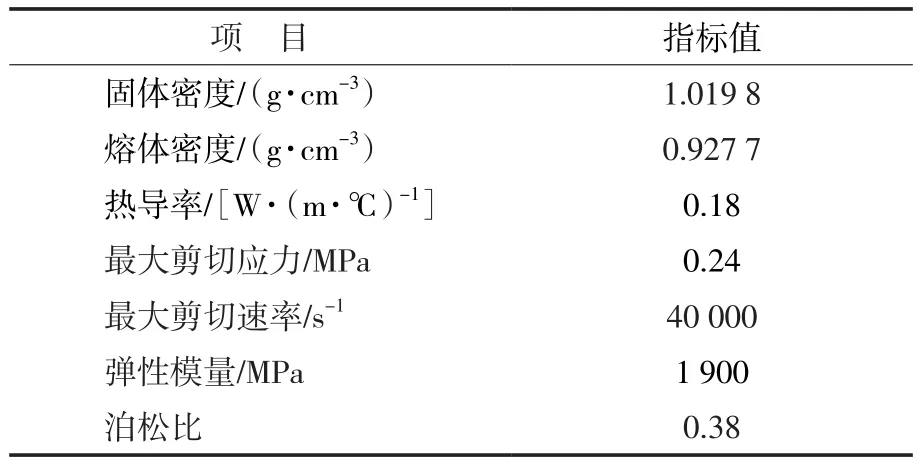
表1 BP Amoco 4018的性能Tab.1 Properties of BP Amoco 4018
1.2 实验指标与设计变量的确定
在实际生产中,旋钮产品不仅要求表面无缺陷,而且由于与其他产品有装配关系,因此对形状和尺寸精度要求较高。本工作选择该产品顶出时的体积收缩率作为实验指标,模具温度、熔体温度、保压压力和保压时间作为分析体积收缩率的设计变量。根据所选材料推荐的工艺参数范围,选择5个水平,实验因素与水平见表2。
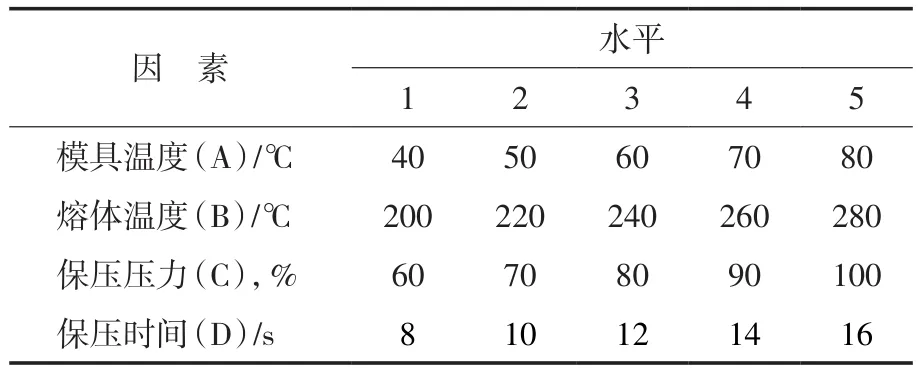
表2 正交试验的因素与水平Tab.2 Factors and levels of orthogonal test
1.3 CCD方法
使用Design Expert数据分析工具进行CCD,将因素、水平和实验目标输入Design Expert数据分析工具中,选择样本点,生成25个实验组合。运用模流分析工具Moldflow软件,根据各设计变量对应的工艺参数,依次对各实验组合进行注塑制品填充、保压、冷却和翘曲分析,得到的体积收缩率分别为12.51%,10.43%,10.10%,8.83%,8.28%,12.54%,9.85%,10.14%,12.15%,9.90%,10.22%,9.03%,8.33%,12.80%,9.91%,12.85%,10.46%,9.10%,12.15%,10.30%,8.37%,10.16%,10.00%,10.34%,10.30%。当模具温度为70 ℃,熔体温度为220 ℃,保压压力为注射压力的90%,保压时间为14 s时,得到的体积收缩率最小,为8.28%。该分析结果仅是CCD下各样本中的最小值,在工艺参数范围内搜索更小的体积收缩率是一项极具现实意义的工作。
2 响应面模型的建立与验证
2.1 响应面模型的建立
响应面模型以其模型简单、构造方便和计算量小等优点成为当前应用极其广泛的拟合模型,该模型构建的关键在于拟合方程阶数的确定。由最小二乘原理可知,拟合精度与拟合方程阶数成反比,因此低阶模型能更好逼近实际响应曲面。由于一阶响应面模型只能表达线性关系,所以在充满非线性问题的实际生产中,二阶响应面模型能以较高拟合精度表达实际曲面。采用二次完全多项式构造近似函数的数学表达式见式(1)。
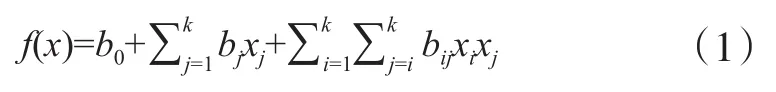
式中:f(x)为注塑件体积收缩率函数;xi,xj为不同水平下的因素值;b0为常数;bj,bij为待定系数;k为工艺参数个数,本文k为4。
式(1)中共有15项待定数,根据CCD的25次实验得到的数据,输入Design Expert数据分析工具,对实验结果进行多次回归拟合分析,得到注塑件体积收缩率的二阶响应模型,见式(2)。

式中:Y为注塑件体积收缩率,%。
2.2 响应面模型验证
由CCD各次实验得到的数据拟合形成的一张响应面模型能否用于表达实际模型,需要对拟合精度等进行检验予以确定。响应面模型通常使用复相关系数(R2)和校正的复相关系数()评价其预测能力。为了考察本工作得到的响应面模型是否可以准确表达设计变量与实验目标值的关系,以检验得到的F统计量(F)和概率(P)为对象分析模型的显著性,以R2和为对象分析模型的拟合精度。体积收缩率的响应面模型方差分析结果见表3。从表3看出:模型的F为46.79,P小于0.000 1,说明使用的二阶响应模型是非常显著的,在统计学上具有一定意义。熔体温度和保压时间的P小于0.000 1,说明熔体温度和保压时间对体积收缩率的影响极为显著。交互项熔体温度和保压时间的P小于0.050 0,说明熔体温度和保压时间的交互作用对体积收缩率的影响显著。由F值和P值可知,各因素对体积收缩率的影响由大到小依次为:保压时间、熔体温度、保压压力、模具温度。
通过对响应面模型的精度进行验证,评价该模型能否作为近似模型。通常用R2和作为评价指标。R2是一个在[0,1]区间内变化的值,R2越接近于1,说明拟合方程精确度越高。R2能够描述响应面的拟合精度,但易受变量数的影响,进而导致预测失真。为了减小该缺陷,需要以对其予以校正。R2和的数学表达式分别见式(3)和式(4)。
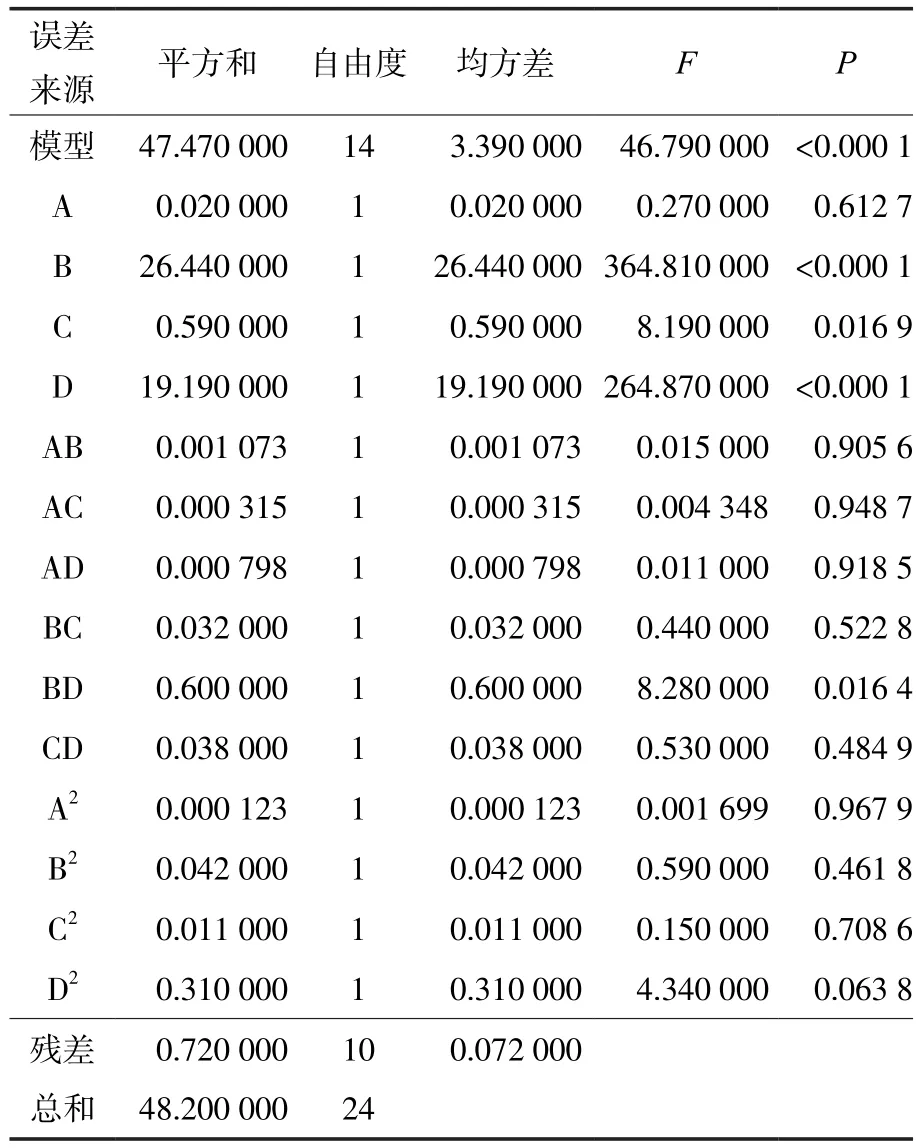
表3 方差分析表Tab.3 Analysis of variance
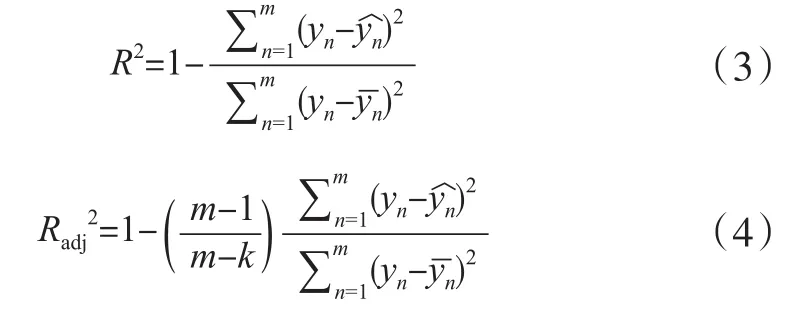
式中:yn为样本采集点;为采样点预测值;yn为预测样本的平均值;m为样本数。
将分析得到的各体积收缩率输入式(3)和式(4),得到体积收缩率的R2为0.985 0,为0.963 9,两个系数均接近于1。这说明拟合得到的响应面模型拥有非常高的拟合精度,由此可以判定实际模型可以由该响应面模型所替代,并且能够较好地预测不同工艺参数组合下的体积收缩率。
3 结果优化与分析
运用Design Expert数据分析工具,模具温度控制在40~80 ℃,熔体温度控制在200~280 ℃,保压压力设定为注射压力的60%~100%,保压时间设置为8~16 s。经过迭代,获取最优注塑成型工艺参数:模具温度为51.271 ℃,熔体温度为206.247 ℃,保压压力为注射压力的95.541%,保压时间为13.214 s,该工艺参数组合下得到的注塑件的体积收缩率为7.901%。与CCD得到的25个样本工艺参数分析结果相比,经过响应面模型优化得到的注塑件的体积收缩率更小,即该产品的品质更佳。
将最优工艺参数组合输入到Moldflow软件中进行分析,得到的体积收缩率为8.086%,模流分析结果见图2。基于响应面模型预测得到的结果与由Moldflow软件分析得到的结果差值为0.185%,具有较高的接近度,故建立的响应面模型具有较高的预测精度。将所需预测的工艺参数输入该响应面模型,便能迅速预测到相应注塑件的体积收缩率,具有极高的运算速度。因此,该方法能准确而高效地预测不同工艺条件下的产品质量,能缩短分析周期,降低反复实验或分析带来的成本。
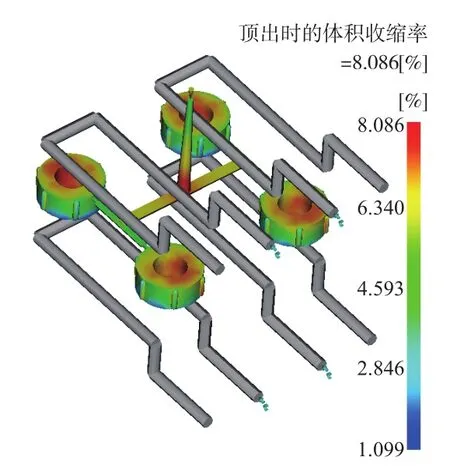
图2 体积收缩率Fig.2 Volume shrinkage
4 结论
a)运用Design Expert数据分析工具进行CCD,使用Mlodflow软件开展注塑件模流分析。对实验结果进行多次回归拟合分析,得到注塑件二阶响应面模型。通过响应面模型拟合误差分析,表明拟合模型具有较高的拟合精度。
b)通过响应面模型能快速得到不同工艺条件下的注塑件质量,且运算速度极高。模流分析技术与响应面模型技术相结合是解决工艺优化问题的一种有效途径。
c)注塑件最佳成型工艺参数组合:模具温度为51.271 ℃,熔体温度为206.247 ℃,保压压力为注射压力的95.541%,保压时间为13.214 s。优化后塑件的体积收缩率为7.901%,产品质量得到了明显改善。
