界面效应对纳米多孔材料宏观弹塑性力学性能的影响

马连华，周靖博，曹亚阔

(1.河北大学 质量技术监督学院，河北 保定 071002；2.河北大学 建筑工程学院，河北 保定 071002)

纳米多孔材料通常是由固体基体和嵌入其中的多个纳米尺度孔构成(孔径一般在100 nm以下).纳米多孔材料由于孔洞界面处的原子晶格结构不同，导致其拥有与基体不同的弹性和张力(称为界面弹性和界面张力).众多学者对此进行了研究，Duan等[1-4]基于Eshelby理论，建立了一个纳米尺度下的细观力学模型,用以研究非均匀材料的界面效应.Feng等[5]利用单胞细观力学模型理论，研究了表面应力与张力对纳米多孔材料有效弹性力学性能的影响.Soyarslan等[6]对多孔金进行数值模拟以研究力学参数对界面效应的影响.

纳米多孔材料在荷载作用下会使孔洞界面上的原子密度和数量发生改变，界面具有明显不同于基体的弹性性质.Zhang等[7]通过考虑界面效应，发展了基于二阶应力矩的细观力学模型，得到了纳米多孔材料的宏观屈服面函数以及单轴载荷下屈服强度表达式，研究了界面残余应力和界面弹性对纳米多孔材料的宏观弹塑性性能的影响.Dormieux等[8]建立了含球形孔洞的纳孔材料非线性均匀化模型，并得到了屈服强度显式表达式.Monchiet等[9]采用极限分析法分析了含界面应力的椭球孔洞对纳米多孔材料宏观屈服强度的影响.Brach等[10]采用分子动力学方法，分别对含长椭球和扁椭球以及球形孔洞的多孔材料宏观力学性能进行了研究，并重点研究了孔洞形状的影响.Moshtaghi等[11]采用细观力学方法，研究了纳米多孔材料的弹塑性力学性能.本文通过建立等效的界面相模型，采用有限元方法研究了界面效应对纳米多孔金属宏观单轴弹塑性力学性能的影响机制.

材料的界面效应常用经典的界面模型来描述.由于该模型中的界面是一种理想的无厚度界面，不便于直接用于有限元模拟，因此，本文首先将传统的界面模型等效为有一定厚度的界面相模型[12]，并建立相应的界面本构模型以采用有限元数值模拟方法研究孔隙率、孔径尺寸及界面残余应力对纳米多孔材料宏观弹塑性力学行为的影响.

1 界面本构模型及其有限元实现

在经典的无厚度数学界面模型中，界面的弹性本构关系可表示为[13]

(1)

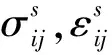
根据界面弹性理论，载荷作用下的界面主要受面内应力作用，界面面积增大或减小，而面外应力可忽略不计.因此，这种面内应力占主导的界面可等效为只考虑面内应力的有一定厚度的界面相模型，进而采用薄膜单元来进行数值研究.为了考虑界面残余应力，引入参数α，可得到等效的具有一定薄膜厚度h的界面相应力-应变关系[14]：

(2)

其中，E为等效界面相的弹性模量，v为等效界面相的泊松比.图1给出了无厚度的数学界面等效为一定薄膜厚度(h)的界面相模型的示意图.

图1 无厚度数学界面与有厚度界面相的等效关系Fig.1 Equivalent relationship between the mathematical interface without thickness and the interface phase with the thickness h

根据式(1)和(2)，可得到下列材料参数对应关系

(3)

2 有限元模型

本文以纳米多孔铝为研究对象，参考Tian等[15]确定界面的相关参数如下:

λs=3.493 9N/m,μs=-5.425 1N/m,τ0=0.568 9N/m,

(4)

其中，σy、h、n(0≤n≤1)分别表示屈服强度、强度系数和加工硬化指数.

采用的铝基体材料参数如表1所示[16].

为方便起见，假设纳米孔在铝基体中呈周期性分布，可选取具有一定孔隙率的体积单元(representative volume element，RVE)为分析对象，以此计算含界面效应的纳米多孔铝的宏观弹塑性力学性能.假设纳米孔洞位于RVE的中心，根据对称性，可取RVE单胞的1/8的模型(图2)进行有限元数值计算.

针对所建立的含界面相的RVE有限元模型，首先施加对称性条件和约束方程，使其满足周期性边界条件，然后施加单轴拉伸和压缩载荷，进而模拟纳米多孔铝RVE的宏细观弹塑性力学性能.

3 宏观弹塑性力学行为

首先，保持孔径尺寸(12 nm)和界面残余应力(0.5689 N/m)一定，对RVE开展单轴加载有限元模拟，计算了孔隙率(f)分别为10%、20%、30%条件下，纳米多孔铝的弹塑性力学变形情况.图3给出了单轴加载作用下纳米多孔铝在不同孔隙率下的应力-应变曲线.容易看出，孔隙率对纳米多孔材料的弹塑性力学性能有明显影响.纳米多孔铝的有效弹性模量和屈服强度随着孔隙率的增加呈现下降趋势.由于界面相的负刚度效应，材料在变形到一定程度呈现出应力软化现象，即随着单轴应变增加，宏观应力降低.例如，对孔隙率为30%的情形，单轴应变达到2%左右会观察到应力软化现象.在孔径一致的情况下，孔隙率越大，表明界面弹性贡献越大，应力软化现象也就越明显.

然后，保持孔隙率(15%)和界面残余应力(0.568 9 N/m)一定，对RVE开展有限元模拟，计算了纳米孔洞孔径R分别为6、8、10 nm情形下，纳米多孔铝的弹塑性力学变形情况.图4给出了不同孔径尺寸下多孔铝单轴应力-应变曲线.孔径尺寸越大，材料有效屈服强度和流动应力越大.孔径越小，界面效应越明显，应力软化现象也越显著.当孔径增大到8 nm和10 nm，由于界面效应减弱，二者对应的应力-应变曲线相差不大.

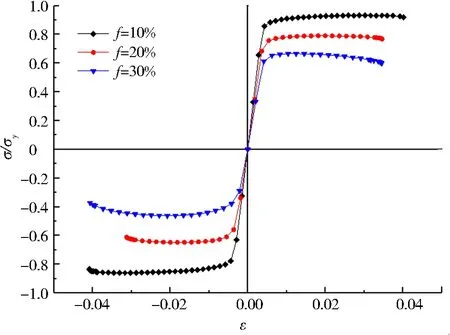
图3 改变孔隙率的多孔铝单轴应力-应变曲线Fig.3 Uniaxial stress-strain curve of porous aluminum with different porosity

图4 改变孔径的多孔铝单轴应力-应变曲线Fig.4 Uniaxial stress-strain curve of porous aluminum with different pore size

最后，保持孔隙率(15%)和孔径尺寸(12 nm)不变，改变界面残余应力τ0对RVE开展有限元数值模拟. 图5给出了多孔铝在不同界面残余应力情形下的单轴应力-应变曲线.容易看出，由于界面残余应力τ0的存在，材料宏观拉伸-压缩曲线呈现出明显的不对称性，τ0越大，拉-压不对称性越明显.该模拟结果与Jin等[17]测定结果具有一致性.在压缩时多孔铝的有效屈服强度和流动应力随界面残余应力的增大而减小，而拉伸情况下纳米多孔铝有效屈服强度和流动应力变化不明显.

图5 改变残余应力的多孔铝单轴应力-应变曲线Fig.5 Uniaxial stress-strain curve of porous aluminum with different interfacial residual stress

4 结 论

本文针对含球形纳米孔洞的多孔金属，引入考虑界面效应的界面相模型，采用有限元模拟方法研究了孔隙率、孔径尺寸、界面残余应力对材料弹塑性力学性能的影响.研究结论如下：

1)纳米多孔金属加载到一定程度，流动应力首先达到一个峰值，然后逐渐减小，这种应力软化效应是由界面的负刚度特性所产生的.

2)其他条件不变时，孔隙率越大，有效弹性模量和屈服强度越小，应力软化越明显.纳米孔径越小，界面效应越显著，应力软化越明显.

3)界面残余应力会引起材料明显的拉压不对称现象.界面残余应力越大，多孔材料压缩时有效屈服强度和流动应力越小，拉伸时则变化不明显.