针对CT系统参数标定和成像建模及算法研究

王有德

针对CT系统参数标定和成像建模及算法研究

王有德

（辽宁工业大学 理学院，辽宁 锦州 121001）

针对最基本的CT系统的成像原理和数据处理分析，用投影边界分析法和插值法对模型展开建立与优化，并得到探测器单元点之间距离、X射线180个方向、未知介质的几何形状和吸收率信息。最后运用MATLAB对提出算法进行仿真验证。通过以上方法，成像时需对参数进行标定，并对未知结构样品进行成像。

投影边界分析法；插值法；MATLAB；CT系统

随着科学技术的不断发展，CT技术在医学影像、农林业、化工和工业无损检测等诸多领域都有着广泛的应用[1-3]。随着对CT系统的研究，出现了许多相关的研究成果。在传统的K-SVD算法基础上，利用双层字典学习方法对图像进行重建，与传统方法相比较，这种方法能恢复更多原始CT图像的细节信息，使图像的质量得到了提升，达到了更好的重建效果[4]。不同的正则化算法被逐渐应用到CT图像重建，不同算法下的图像重建效果不同，相比于其他算法双边总变分正则化算法[5]的图像重建效果最好。基于指数形式的滤波函数(EBFF)重建图像，相比于上述文献中提出的方法，指数形式的方法得到的图像更逼真[6]。更先进的科研级CCD相机和非晶硅平板探测器的2种典型三维CT系统和以上2套三维CT在生物医学和工业无损检测中的部分应用结果也得到了研究[7]。上述文献仅对CT图像重建算法进行了优化或是对CT图像技术在相关领域的应用进行了研究。然而，CT图像的成像原理和CT系统参数的标定在研究相关问题本质，尤其是计算详细数据时是非常重要的，这也正激发了本文运用边界分析法和插值法对其进行研究。由于CT系统在安装过程中存在误差，对所建物体影像质量有所影响，因此成像时需对参数进行标定。

本文以2017年全国大学生数学建模竞赛题目为例，对CT系统参数标定及成像原理进行主要研究。

1 模型假设

假设X射线在传播过程中能量不受除模型之外的其他影响。

假设不考虑单束射线的宽度。

假设经过椭圆长轴的射线与光的吸收图波峰接近重合。

假设经过椭圆和小圆横轴的射线与光的吸收图波峰接近重合。

假设忽略光的衍射现象。

假设X射线转动180次视为等角度旋转。

假设标定模板中心为质点。

2 问题一—建模与求解

本节的主要任务是对CT系统的参数进行标定，本文对2种情况进行考虑。第一种情况，假设托盘中心位置即为系统旋转中心的位置，由于共给定512个探测器单元，所以此时旋转中心坐标对应的探测器应为第256个探测单元位置，可此处与波峰并不是对应关系，因此得到系统旋转中心与托盘中心不重合的结论，情况一的假设不成立。在第二种情况下，假设系统的旋转中心与托盘中心存在偏离，设定旋转中心横坐标、纵坐标、旋转中心与托盘中心的水平距离和垂直方向距离。根据水平距离、垂直距离和每个探测器单元点距离代数关系，计算出相应数据，即为旋转中心坐标。接着，从发生干涉的数据考虑，2条射线射向圆形介质时会出现有限列数据，小圆直径已知，后者与前者的比值即为检测器单元之间的距离。由前面的分析得出结论：每一列对应一个方向，投影最宽的位置应该对应射线垂直长轴的方向，最窄的地方应该对应射线平行长轴的方向。将平行长轴方向定义为0°方向，将0°与90°的线在图中表示出来。通过MATLAB可计算出0°与90°所在列号，得到平均转动次数，从而可计算出180次转动的方向。

针对问题一，本文依据投影原理，对所给数据进行多层次分析，运用MATLAB软件将这些数据绘制为标定接收强度光波图，同时建立了几何模型，对几何模型进行分析，得到模板示意图位置和数据中不为0位置大致为一一对应的关系。建立笛卡尔坐标系，利用投影边界法、中心射线法原理以及几何关系，通过设计标定模板来接收与数据信息对应的物理图形，进而得到旋转中心坐标、各个探测器单元之间的距离。

步骤1 对数据进行位置投影分析并建立几何模型。

附件2有512行170列数据，部分数据为零，剩余数据都非零。定义零数据吸收率为0，非零数据吸收率为1。针对附件1，首先利用EXCEL表格筛选功能，对所给附件中的数据进行筛选处理，筛选后得到如图1所示的图像。其中，白色表示吸收率为0的部分，粉色则表示吸收率为1的部分。

由于图1只能反映吸收强度的大致图像，而不能反居民点映吸收强度的大小。因此，为了更精确反映出各部分对光的吸收强度，利用MATLAB软件做插值，绘制出了如图2所示的模板在旋转过程中的边缘图像。图像中颜色的深浅反映了吸收强度的大小，即图像颜色越深，标定模板对光的吸收强度越大，反之，对光的吸收强度越小[8]。

图1 附件2数据的边缘

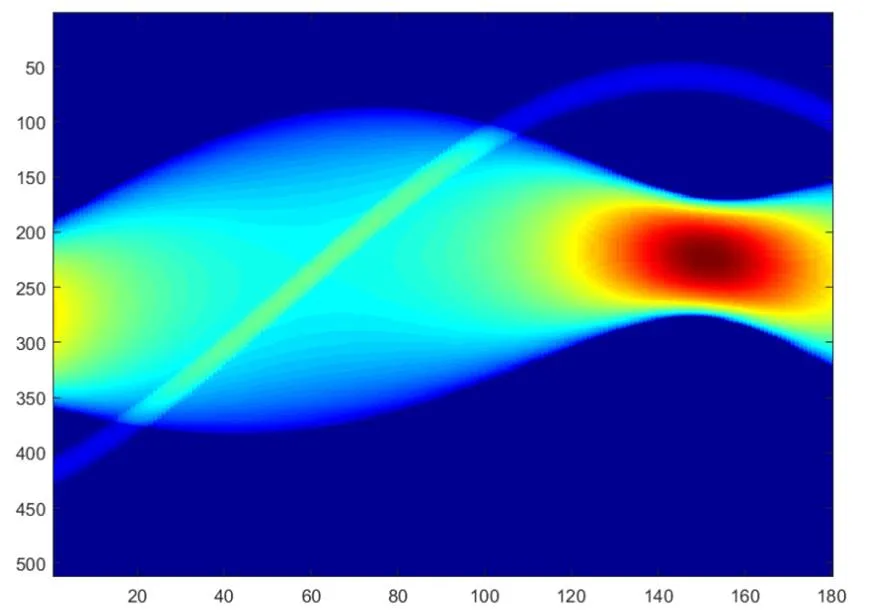
图2 旋转过程边缘图像

根据X射线强度衰减与图像重建的数学原理公式[8]，建立以下公式：

式中：表示X射线强度衰减率，表示穿过介质的射线长度。

当X射线具有的能量一定时，衰减系数随着射线穿过介质材料不同而变化。比如软组织的衰减率比骨骼小，因此X射线能量在骨骼中衰减得更快些。

其中，Δ表示每个探测器单元点之间的距离。此公式中每个单元点之间距离等于小圆介质的直径与附件二有限列数据的列数的比值。

由上述2个公式联立可得出每个探测器单元点之间的距离Δ=0.2857。

步骤2 绘制特殊位置的标定模板对光波的吸收图。

根据步骤1中对数据的分析，将探测器得到的512行数据进行编号，得到探测器在219号和235号吸收率最大。对应的吸收强度是在139次和61次，然后用MATLAB对这2个特殊位置做光波吸收图(椭圆长轴光波图见图3，通过圆形和椭圆形最大长度光波图见图4)。

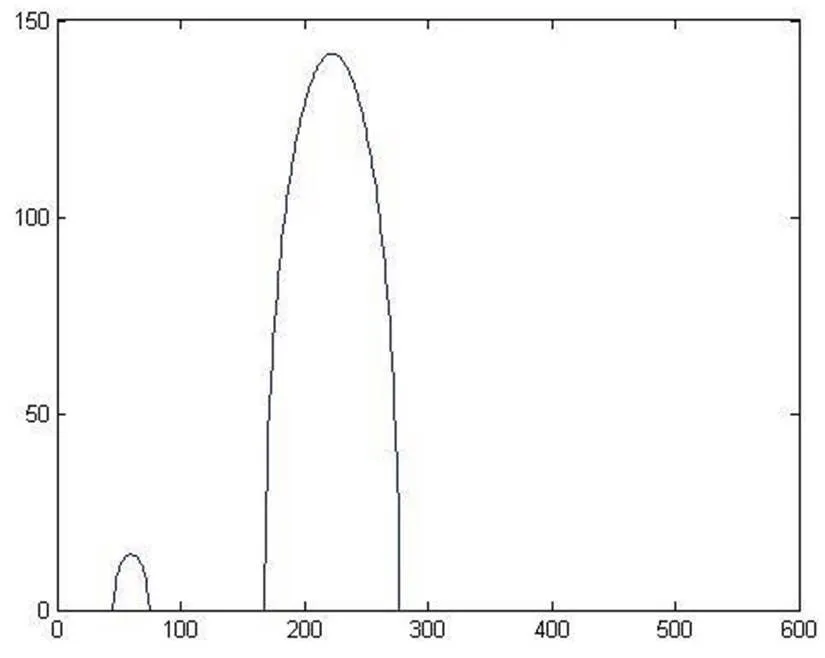
图3 椭圆长轴光波

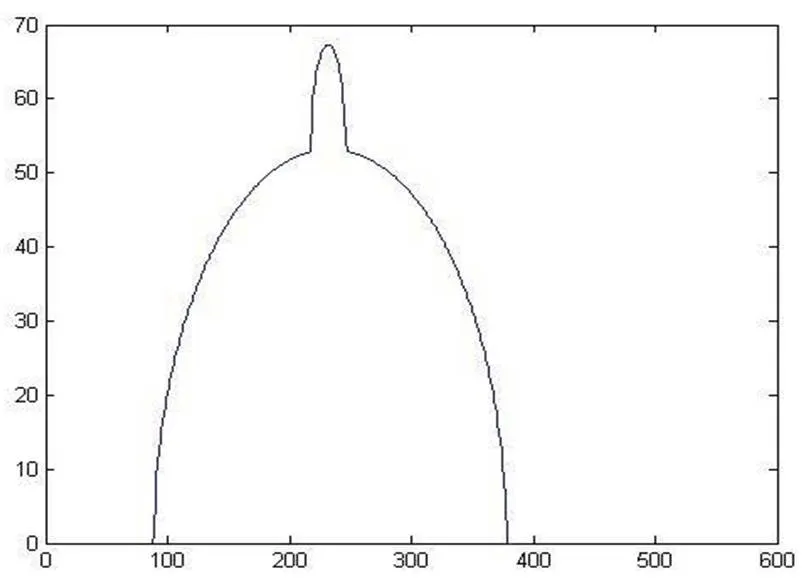
图4 通过2种介质最大长度光波图

根据波峰考虑，CT系统旋转中心与托盘中心存在偏离，在水平方向上距离为Δ，在垂直方向上距离为Δ。根据几何关系公式：

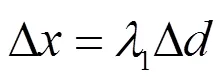
水平方向偏离值等于探测器单元点个数与每个探测器单元点之间距离的乘积。从而便可得到如下在水平方向上偏离值：

垂直方向偏离值等于探测器单元点个数与每个探测器单元点之间距离的乘积。那么就可得到在垂直方向上的偏离值：

CT系统旋转中心横坐标为一半模板长与水平方向偏离值的差。由于是差值，因此该点在水平方向是在托盘中心的左面：

CT系统旋转中心纵坐标为一半模板宽与垂直方向偏离值。因为差值是通过加法得到，所以该系统旋转中心在垂直方向托盘中心的上方。

根据公式(3)~(6)，求得系统旋转中心的坐标(39.7148，55.714)。

步骤3 结合前面分析，用MATLAB和CAD软件对附件2和附件1做出几何模型。将2个模型在平面做出关联(详见图5)。

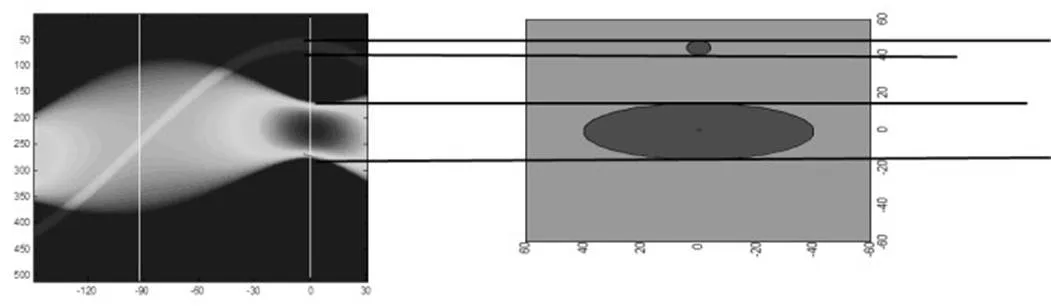
图5 几何模型投影图

由分析可得出结论：每一列对应一个方向，投影最宽的位置应该对应射线垂直长轴的方向，最窄的地方应该对应射线平行长轴的方向。将平行长轴方向定义为0°方向，将0°与90°的线在图中表示出来。通过MATLAB可计算出0°与90°所在列号，得到平均转动次数，从而可计算出180次转动的方向。

由于MATLAB只能单一做出几何模型，所以结合CAD作图更能生动形象具体表示这180个方向的存在范围。通过MATLAB可以计算出0°所在列号为151，-90°所在的列号为58，即90°旋转了93次，可计算出平均每次转动0.9677°。由此可计算出180次转动的方向。方向结果详见表1和表2。

表1 前90组X射线方向

探测单元编号角度探测单元编号角度探测单元编号角度探测单元编号角度探测单元编号角度探测单元编号角度1-146.122716-131.607231-117.091746-102.576261-88.060776-73.54522-145.15517-130.639532-116.12447-101.608562-87.09377-72.57753-144.187318-129.671833-115.156348-100.640863-86.125378-71.60984-143.219619-128.704134-114.188649-99.673164-85.157679-70.64215-142.251920-127.736435-113.220950-98.705465-84.189980-69.67446-141.284221-126.768736-112.253251-97.737766-83.222281-68.70677-140.316522-125.80137-111.285552-96.7767-82.254582-67.7398-139.348823-124.833338-110.317853-95.802368-81.286883-66.77139-138.381124-123.865639-109.350154-94.834669-80.319184-65.803610-137.413425-122.897940-108.382455-93.866970-79.351485-64.835911-136.445726-121.930241-107.414756-92.899271-78.383786-63.868212-135.47827-120.962542-106.44757-91.931572-77.41687-62.900513-134.510328-119.994843-105.479358-9073-76.448388-61.932814-133.542629-119.027144-104.511659-89.996174-75.480689-60.965115-132.574930-118.059445-103.543960-89.028475-74.512990-59.9974

表2 后90组X射线方向

探测单元编号角度探测单元编号角度探测单元编号角度探测单元编号角度探测单元编号角度探测单元编号角度 91-57.0943106-42.5788121-28.0633136-14.5155151016614.5155 92-56.6654107-41.6111122-27.0956137-13.54781520.967716715.4832 93-55.1589108-40.6434123-26.1279138-12.58011531.935416816.4509 94-54.1912109-39.6757124-25.1602139-11.61241542.903116917.4186 95-53.2235110-38.708125-24.1925140-10.64471553.870817018.3863 96-52.2558111-37.7403126-23.2248141-9.6771564.838517119.354 97-51.2881112-36.7726127-22.2571142-8.70931575.806217220.3217 98-50.3204113-35.8049128-21.2894143-7.74161586.773917321.2894 99-49.3527114-34.8372129-20.3217144-6.77391597.741617422.2571 100-48.385115-33.8695130-19.354145-5.80621608.709317523.2248 101-47.4173116-32.9018131-18.3863146-4.83851619.67717624.1925 102-46.4496117-31.9341132-17.4186147-3.870816210.644717725.1602 103-45.4819118-30.9664133-16.4509148-2.903116311.612417826.1279 104-44.5142119-29.9987134-15.4832149-1.935416412.580117927.0956 105-43.5465120-29.031135-14.5155150-0.967716513.547818028.0633

3 问题二—建模与求解

针对问题二，运用MATLAB对附件2数据处理并计算得到入射角度。根据X射线强度衰减与图像重建原理，并进行radon变换[9]。根据radon函数得到的吸收强度图像颜色深浅判断介质为不规则的，并能找出椭圆4个边界点坐标，进而求得未知介质在托盘中的位置。结合MATLAB生成介质吸收强度图，运用插值法计算得到10个点的吸收率。

步骤1 利用问题1的方法，对未知介质进行位置预判断。

图6 Radon变换平面示意图

将附件3中的数据导入到MATLAB中，利用radon函数生成未知物质在该平面上的吸收强度图像，如图6所示。

图中白色圆圈为托盘中心位置，以白色圆点为起始点，向左平移50，向右平移50，向上平移50，向下平移50所形成的白色方框即为正方形托盘所在位置。蓝色部分为吸收强度为0。

将附件3的数据导入MATLAB中，利用imagesc函数生成未知介质吸收强度图，见图7。

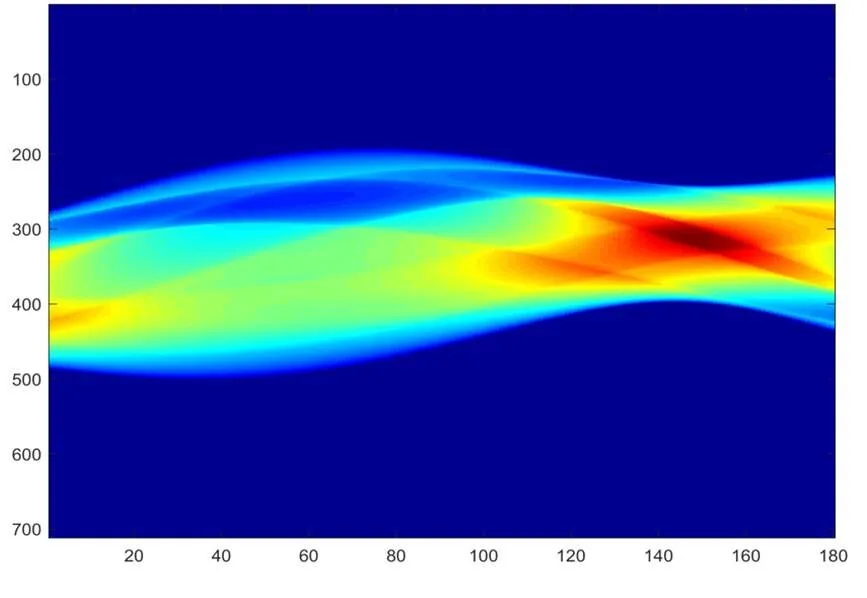
图7 未知介质吸收强度图

此图反映X射线穿过未知介质不同位置对其吸收强度的不同，颜色深表示该点吸收强度大，反之强度小。

根据图6可以判断，蓝色部分为吸收强度为0的点，可视为空气所在位置，无吸收(吸收率为0)，为了确定位置物体中心，将图6图像二值化，得到图8。利用MATLAB找出椭圆中的4个边界点坐标。

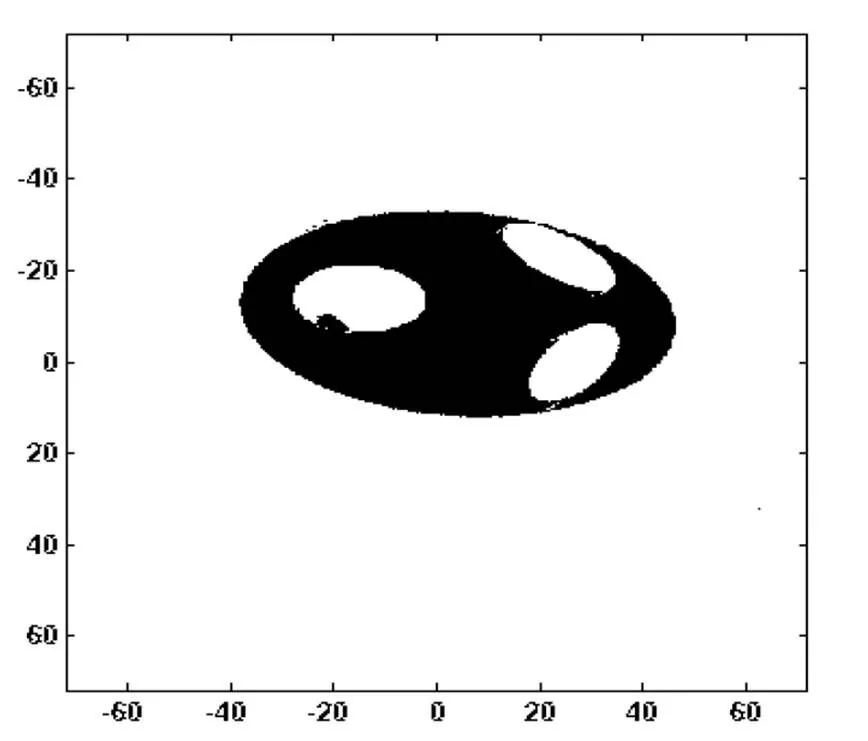
图8 二值化后图像

根据X射线能量衰减规律与图像重建原理，X射线强度和入射强度公式可表达为：

此公式表示X射线穿过均匀的材料介质时，能量衰减率与能量本身呈正比。

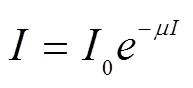
其中，0表示X射线入射强度。此公式表示当X射线的能量一定时，衰减系数会随着射线穿过介质材料的不同而发生指数趋势的变化。

计算图8中红色区域距离椭圆中心的距离，根据几何关系，计算出未知介质中心相对于模板托盘中心的位置，从而可得未知介质的坐标(1,1)。将附件中的数据导入，经MATLAB计算，得出中心坐标为(204.5, 211.5)。

步骤2 利用坐标变换及插值法，求出吸收率。

由图6可知该不规则物体为一个非均匀介质的物体[10]，用MATLAB做出附件1收率的几何模型，吸收率由图中不同颜色表示，见图9。

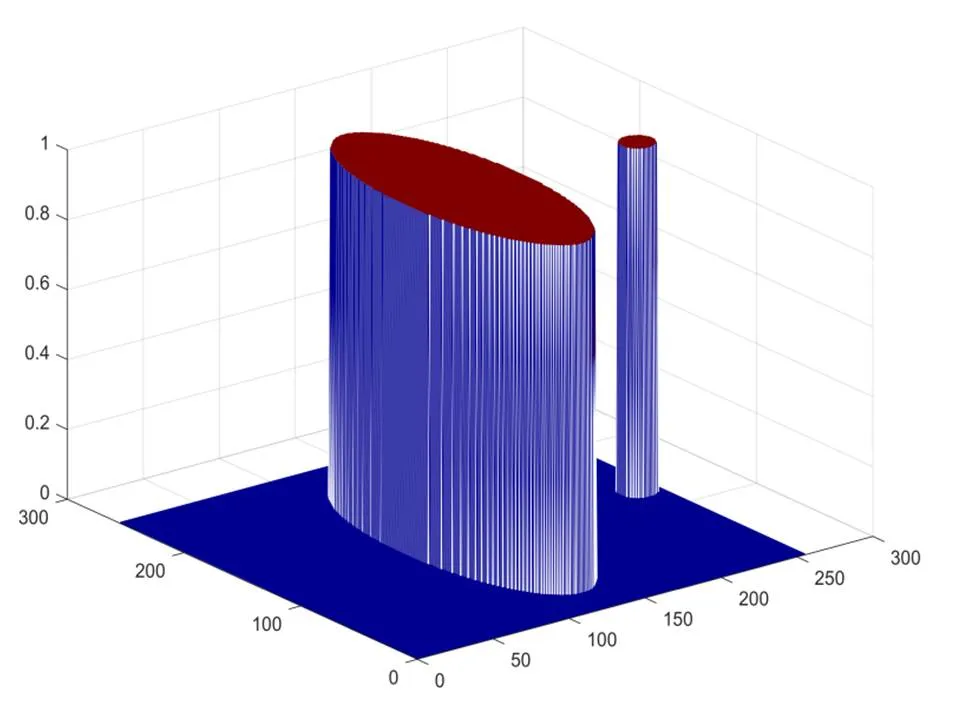
图9 附件1的吸收率

此图反映不同颜色具有不同吸收率，但并不能反映具体数值。于是用MATLAB对变化后的数据做出几何模型，见图10。

图10 附件1数据中坐标变化后的吸收率

由图10可知颜色深吸收率大，反之颜色浅吸收率小，最大吸收率为=1(表示变换前吸收率)，'=0.5('表示变换后吸收率)。根据吸收率公式：

(9)

其中，表示吸收率比值。由此公式可以得到，图8中蓝色区域的吸收率为0，橙色区域的吸收利率为1，红色椭圆区域较大的部分吸收率为1.3，较小部分的吸收率为1.2，重叠部分的吸收率为1.5。

利用下面公式对附件3中10个点的坐标进行变换：

已知角'=29.663，=198.7114，=216.6240。其中，表示横坐标变换常数，表示纵坐标变换常数。

得到变换后点的坐标如表3所示，由表可以看出10点的位置，通过对吸收强度矩阵中位置的查找，并使用插值法求出10点在吸收强度中的值如表3。

表3 坐标变换

原坐标 变换后的坐标 吸收强度 xyx'y'Q'Q 101816.3792188.39960.00860.0172 34.525105.4620166.32920.00280.0058 43.533147.9214175.17860.48250.9652 4575.5228.8226305.24370.00110.0024 48.555.5203.8892236.49400.49360.9872 5075.5244.4408296.27720.00210.0044 5676.5264.9760288.64070.00390.0078 65.537223.8150148.22040.56101.1222 79.518233.473267.76450.01550.0312 98.543.5338.5521109.34460.02350.0470

结论：运用MATLAB和图形几何关系得出物质中心位置为(204.5, 211.5)，几何形状为一个大椭圆物体在一侧有2个小椭圆孔，10个点的吸收率为0.0172、-0.0058、0.9652、0.0024、0.9872、-0.0044、0.0078、1.1222、0.0312、0.0470。

4 结论与展望

基于以往文献，研究了如何在给定数据下求得CT系统旋转中心位置、各个探测器单元之间的距离、该CT系统使用的X射线的180个方向角度、未知介质的几何形状以及10个位置处的吸收率的问题。特别地，对于确定旋转中心坐标使用曲线积分处理。进而，运用投影边界法，将圆形介质直径与不发生干涉介质的有限数据列数做比值，求得探测器单元之间的距离。其次，运用radon变换和radon逆变换的数学知识求出未知介质几何形状。最后利用MATLAB软件确定未知介质10个位置的吸收率。但本模型中考虑的X射线的旋转角度不能达到真正意义上的90°，因此克服这一误差问题仍亟待解决。本文提出的边界分析法已成功应用于商业领域，因此对于想步入这一行列的单位及个人，系统地研究此算法是必要的，对其发展具有深远意义。

[1] Carrino J A, Al Muhit A, Zbijewski W, et al. Dedicated cone-beam CT system for extremity imaging[J]. Radiology, 2014, 270(3): 816-824.

[2] Udawatta R P, Anderson S H. CT-measured pore characteristics of surface and subsurface soils influenced by agroforestry and grass buffers[J]. Geoderma, 2008, 145(3/4): 381-389.

[3] Wirtz S, Popp V, Kindermann M, et al. Chemically induced mouse models of acute and chronic intestinal inflammation[J]. Nature Protocols, 2017, 12(7): 1295.

[4] 朱雪茹, 李勇明, 李传明, 等. 基于双层字典学习的低剂量CT图像重建算法[J]. 北京生物医学工程, 2017, 36(6): 584-590.

[5]李帆, 李勇明, 李传明, 等. 正则化算法在CT图像重建上的应用[J]. 计算机系统应用, 2017, 26(2): 143-147.

[6]马思汉, 张催, 陈章谷, 等. CT图像重建中基于指数形式的滤波函数优化[J]. 无损检测, 2017, 39(12): 1-6.

[7]王贤刚, 叶青, 郭志平, 等.两种典型三维CT系统及应用[J]. CT理论与应用研究, 2009, 18(4): 26-33.

[8]张雄, 黄廷皓, 张永娟, 等. Image-Pro Plus混凝土孔结构图像分析方法[J]. 建筑材料学报, 2015, 18(1): 177-182.

[9]曾有良. Radon变换波场分离技术研究[D]. 青岛: 中国石油大学, 2007.

[10] 樊计昌, 王夫运, 刘明军, 等. 横向非均匀介质Q值层析成像方法、软件及应用[J]. CT理论与应用研究, 2013, 22(2): 255-264.

Research on Parameter Calibration and Imaging Modeling and Algorithm of CT System

WANG You-de

（College of Science, Liaoning University of Technology, Jinzhou 121001, China）

In this paper, according to the imaging principle and data processing analysis of the most basic CT system, the projection boundary analysis method and interpolation method are used to develop and optimize the model, and the distance between the detector unit points, 180 directions of X-ray, geometric shape and absorption rate of unknown media are obtained. Finally, the proposed algorithm is simulated and verified by MATLAB. Through the above methods, parameters need to be calibrated during imaging, the unknown structure of the sample imaged.

projection boundary analysis; interpolation method; MATLAB; CT system

O29

A

1674-3261(2021)02-0084-06

10.15916/j.issn1674-3261.2021.02.004

2020-10-07

王有德(1965-)，男，吉林吉林人，副教授，硕士。

责任编校：孙 林