基于遗传算法轮毂盖卡扣优化设计

张晓光，鲁 琪，张振闯

基于遗传算法轮毂盖卡扣优化设计

张晓光，鲁 琪，张振闯

（辽宁工业大学 机械工程与自动化学院，辽宁 锦州 121001）

以某型号轮毂盖为例，分析了带有卡扣特征的轮毂盖结构中的关键技术，利用ANSYS软件完成了卡扣部分的有限元分析，得到卡扣结构参数、作用力、位移和应力等相关的数据，利用Design-Expert软件进行了二元多项式的回归分析，然后利用遗传算法进行优化分析，从而完成了卡扣部分的多目标优化设计。结果表明：遗传算法能快速有效地获得卡扣结构优化设计问题的最优解，优化后的轮毂盖结构结构紧凑、工作稳定，同时也为产品结构的多目标优化提供了参考。

轮毂盖；卡扣；遗传算法；多目标优化

随着现代计算机技术的不断提高，汽车行业飞速发展，以有限元技术为基础的结构受力分析作为产品设计的有力手段不断成熟，以某厂家的轮毂盖设计中发现了卡扣部分有断裂的现象，利用计算机技术进行轮毂盖的优化设计，以达到结构紧凑、工作稳定的目的[1-3]。

本文主要以轮毂盖的结构为研究对象，针对容易断裂的位置进行应力分析，利用数据回归Design Expert软件进行二元多项式的回归分析，利用Isight软件进行卡扣部分的优化分析，结合遗传算法对轮毂盖卡扣的结构参数进行了多目标优化，最终达到优化的目的。

1 汽车轮毂盖结构分析

汽车轮毂盖塑件的整个制品平均壁厚3.0 mm，且形状比较复杂，不易于成型。塑件高度48.00 mm，可使用较小的脱模斜度。轮毂盖塑件为与外界直接接触类零件，对于零件的耐腐蚀性耐磨性能有要求，材料为ABS，相对密度为1.06 g/cm3，应具有较强的抵抗破坏的能力，轮毂盖结构如图1所示。

图1 汽车轮毂盖三维图

2 轮毂盖卡扣响应面模型

2.1 选择优化参数

根据轮毂盖卡扣截面特点，确定优化目标为轮毂盖质量、应力，确定输入变量，如图2所示，选择参数如下：应力、质量相关参数为变形，卡扣厚度，卡扣连接长度，卡扣伸出长度。

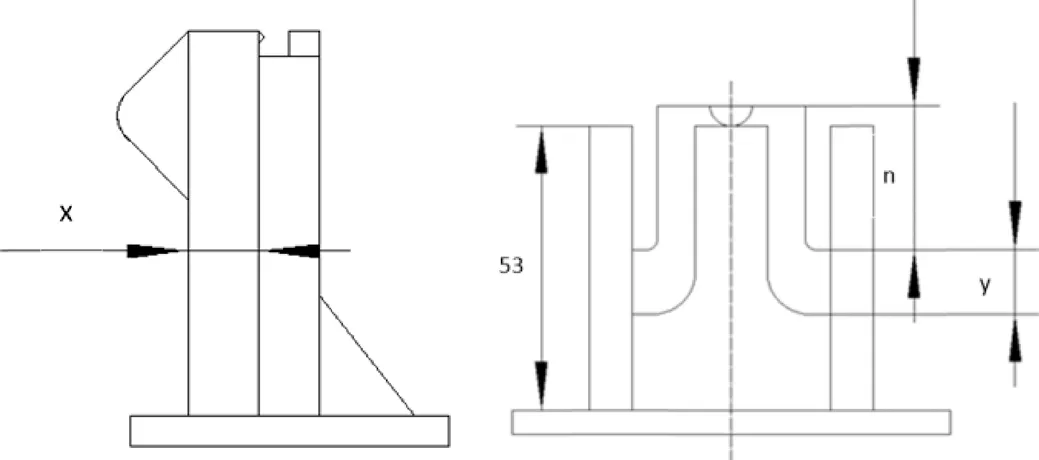
图2 卡扣部分截面图

利用Pro/E软件进行卡扣部分的参数化设计，ANSYS软件进行受力分析，如表1所示。

2.2 数据模型创建

利用多项式函数拟合设计空间的一种优化方法，选择二元多项式作为优化分析的数学模型[4-6]，多项式如下:

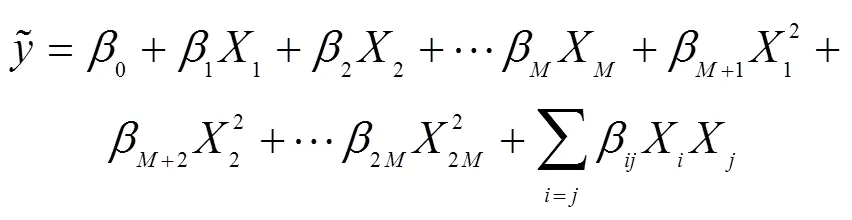
表1 卡扣分析数据样本表

12345678910111213 x/mm2.72.52.52.52223333.53.53.5 y/mm17171014171014101417181510 n/mm26262624224036303610102025 M/g344.94344.27342.66343.23342.03343.31343.48344.87347.22342.59344.04345.99345.13 def/mm3.53.563.783.693.923.654.334.24.43.943.693.883.67 S/MPa9.46511.13813.78113.79713.46923.6521.8279.89414.74314.6168.0555.8567.792

2.3 确定初始值及边界条件

根据现有轮毂和轮毂盖的安装位置，结合厂家的设计要求，卡扣厚度的尺寸在平均壁厚尺寸3 mm左右，卡扣连接长度的尺寸要根据现有五菱宏光轮毂盖卡扣部分尺寸的极限位置，卡扣伸出长度的尺寸不能超过上下极限位置确定初始值，具体数值如表2所示。

表2 设计参数表

变量初始值下极限上极限 x/mm2.723.5 y/mm171018 n/mm261040 Def/mm3.52.55 S/Mpa9.465021.5 M/g344.94338.99349.85

2.4 数据回归方程

2.4.1 质量回归方程

利用回归Design Expert软件拟合后2为0.9882，调整后2为0.9822，如表3所示。

线性曲线拟合最终的模型表达式为：

表3 回归数据表

coefficientdfFp C+329.71934166.91<0.0001Sig x+2.1327141.530.0002 y+0.26091118.27<0.0001 n+0.086116.260.0368 x*n+0.0399111.570.0093

通过各影响因素的分析，得到质量的响应面模型如下图3所示。

由图3可知，在(a)图中，当尺寸处于水平中心位置时，当参数较大时，的尺寸对质量有变化，此时正向趋势变化，比较平缓；当参数较大时，的大小对于质量的影响很明显，此时正向趋势变化，趋势比较陡峭；在(b)图中，当尺寸处于水平中心位置时，当参数较大时，的厚度尺寸对质量有影响，成正向增加趋势，变化范围为340~350 g；当参数较大时，的大小对于质量的影响很明显，变化范围为344~350 g，对比以上图可以发现，3个参数影响关系如下：>>，与的质量响应曲面更为陡峭，说明对参数的变化较参数反应更为显著。

2.4.2 应力回归方程

利用数据回归Design Expert软件拟合后的2为0.9288，调整后2为0.9051，线性拟合结果表4。

表4 线性拟合数据表

coefficientdfFp C+39.76509339.14<0.0001Sig x-5.87182135.790.0002 n-1.22194124.670.0008 C2+0.0282132.930.0003

通过各影响因素的分析，得到应力的响应面模型，如下图4所示。

由图4可知，在(a)图中，当尺寸处于水平中心位置时，当参数较大时，的厚度尺寸对应力有变化，变化趋势比较平缓，先负向趋势变化，然后正向趋势变化，趋势变化范围10~15 MPa之间；当参数较大时，的大小对于应力的影响很明显，并且成负向趋势变化，趋势变化范围15~24 MPa之间；在b图中，当尺寸处于水平中心位置时，当参数较大时，尺寸对应力影响基本没有影响；当参数较大时，的大小对于应力有影响，先负向趋势变化，然后正向趋势变化，趋势变化范围13~20 MPa之间。对比以上3幅图可以发现，3个参数影响关系如下：>>，与的应力响应曲面更为陡峭，说明对参数的变化较加反应更为显著。

通过线性回归分析可以得到的回归方程：

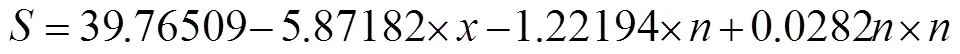
3 轮毂盖多目标优化设计

3.1 多目标优化数学模型

利用软件进行目标优化问题求解，可以得到一组设计变量、最优设计变量的取值及预测结果的信息[7-9]，轮毂盖卡扣部分优化的多目标优化数学模型可以表示为：

3.2 多岛遗传优化

利用多学科设计优化软件ISight对卡扣结构进行优化设计，得出当满足最优目标时，优化结果：输入参数为：=2.0004 mm,=10.351 mm,=17.929 mm，输出数据为：=15.176，=339.66 g, 分析结果如图5。

3.3 优化结果分析

利用优化ISight集成软件优化结果，利用多岛遗传算法优化后的质量为339.66 g，原设计质量为360.85 g，如下表5所示。

表5 设计参数表

项目名称质量/g降低百分比/% 1原设计360.85— 2多岛遗传算法339.665.872

由表5可知，多岛遗传算法法降低了质量百分比为5.872%，由于前期设计参数不合理导致的，没有把原始设计参数的选择范围考虑在内，通过优化分析轮毂盖得到较大提升，满足了产品的多目标优化设计要求，同时也达到了结构优化及性能的要求。进一步通过实验室的验证，卡扣部分的受力明显降低，提高了轮毂盖的使用寿命。

4 结论

（1）以轮毂盖的质量和应力为设计目标，通过卡扣结构的参数化设计，利用ANSYS软件分析相应的数据样本，通过非线性回归软件Design Exper来完成应力和质量回归，分析相应的响应曲面，得到各设计变量的影响关系。

（2）利用优化分析软件ISight结合多岛遗传算法，对卡扣结构进行多目标优化，设定应力为限制条件，保证多目标优化算法能够快速地收敛，经优化后的轮毂盖重量比优化前降低了5.872% ，实现了轮毂盖结构优化的目的。

（3）通过以上方法优化后得到的轮毂盖经过实验室的测试，在安装过程中卡扣部分在达到要求的变形条件下，危险位置所受到的应力明显变形，从而有效的避免了卡扣部分断裂的发生，提高了卡扣的使用寿命。

[1] 王晓龙, 丁文捷, 周军. 塑料卡扣可靠性分析[J]. 现代塑料加工应用, 2016, 28(5): 41-44.

[2] 柏秋阳, 王辉, 郝旭飞, 等. 汽车内饰塑料卡扣配合结构设计研究[J]. 塑料工业, 2015, 43(9): 50-53, 56.

[3] 欧相麟, 王大中, 宁凯军. 汽车注塑件典型缺陷分析及其解决措施[J]. 工程塑料应用, 2014, 42(1): 51-55.

[4] 高志华. 悬臂型塑料卡扣的设计[J]. 塑料科技, 2013, 41(8): 74-77.

[5] 林权, 何靓, 吴雄飞, 等. 卡扣塑件分析及其创新成型模具设计[J]. 塑料科技, 2013, 41(7): 85-89.

[6] 赵明, 王英资, 侯珏, 等. 改进的遗传算法在汽车故障诊断中的应用[J]. 计算机测量与控制, 2020, 28(1): 35-40.

[7] 张浴华. 基于CAE技术的汽车塑件注塑成型过程中遗传算法的应用探讨[J]. 塑料工业, 2019, 47(12): 62-65.

[8] 刘月云. 基于响应面法与Pareto遗传算法的注塑模冷却水道参数优化[J]. 中国塑料, 2019, 33(9): 67-71, 115.

[9] 黄海跃, 范希营, 李赛, 等. 基于神经网络和遗传算法的薄壳塑件注塑工艺优化[J]. 塑料, 2019, 48(3): 66-69.

Optimization Design of Clasp for Hub Cover Based on Genetic Algorithm

ZHANG Xiao-guang, LU Qi, ZHANG Zhen-chuang

（College of Mechanical Engineering and Automation, Liaoning University of Technology, Jinzhou 121001, China）

Taking a certain type of hub cover as an example, this paper analyzes the key technology in the hub cover structure with buckle features, completes the finite element analysis of the buckle part with ANSYS software, obtains the relevant data of buckle structure parameters, forces, displacements and stresses, carries out the regression analysis of binary polynomials with design expert software, and then optimizes the analysis with genetic algorithm and completed the multi-objective optimization design of the buckle part. The results show that the genetic algorithm can quickly and effectively get the optimal solution to the optimal design problem of the buckle structure. The optimized structure of the hub cover is compact and stable, which provides a reference for the multi-objective optimization of the product structure.

hub cover; buckle; genetic algorithm; multi-objective optimization

TQ330.4

A

1674-3261(2021)02-0071-04

10.15916/j.issn1674-3261.2021.02.001

2020-06-03

辽宁省重点研发计划指导计划项目（2018106005）；辽宁省教育厅一般项目（L2015231）

张晓光(1977-)，男，辽宁铁岭人，副教授，硕士。

责任编校：刘亚兵