室内无线定位场景下改进多项式拟合的非视距误差识别算法

朱雯婷，邹德财1,,4，尹婷

室内无线定位场景下改进多项式拟合的非视距误差识别算法

朱雯婷1,2,3，邹德财1,3,4，尹婷1,2,3

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院大学 电子电气与通信工程学院，北京 101048；3. 中国科学院 精密导航定位与定时技术重点实验室，西安 710600；4. 中国科学院大学 天文与空间科学学院，北京 101048）

由于全球导航卫星系统（GNSS）无法解决在室内场景下定位问题，室内定位技术应运而生，UWB、WiFi等室内定位技术在许多领域得到广泛应用。虽然这些技术在视距传播时能满足室内定位需求，但是由于墙体等障碍物而产生的非视距误差，使得定位性能急剧下降，从而无法达到室内定位需求的精度。为克服非视距传播带来的定位误差和现有识别算法实时性低的问题，本文提出了基于改进的多项式拟合的非视距误差识别算法。首先利用多项式拟合鉴别测量值中的非视距误差并且预测距离，通过拟合曲线和测量值之间的偏差来识别非视距误差，检测阈值可以根据测量值自适应的调整。然后利用卡尔曼滤波器处理测量值，在非视距传播下，对测量值进行加权重构。实验结果表明，在非视距环境下，该算法的复杂度低，并且该算法的均方误差较传统多项式拟合的非视距识别算法降低了13.65%，有效抑制了非视距误差的影响。

室内定位；非视距误差识别；多项式拟合；卡尔曼滤波

0 引言

随着移动通信技术的发展，利用移动通信网对移动用户进行定位引起了广泛关注，各种无线定位服务业务应运而生[1]。虽然无线定位服务得到了很大的发展，但无线定位领域仍存在许多亟待解决的问题，消除测距中非视距因素导致的定位误差是目前存在的问题之一。在很多场景下，电波信号的传播为非视距传播，会使基于到达时间（timeof arrival，TOA）测量值产生一个正的附加超量时延[2]，从而导致对未知节点的位置估计存在较大偏差。非视距（non-line-of-sight，NLOS）误差是无线传感器网络定位时最主要的误差来源[3-4]。因此，在无线传感器网络定位中，如何消除TOA测量值中NLOS误差，提高定位精度成为关键问题。

NLOS识别的基本思想是选取适当的判决变量并进行假设检验，判决变量必须在LOS和NLOS环境下有明显区分。常用的识别方法有Wylie识别算法[5]、残差分析判决法[6]、假设检验判决法[7]以及基于三阶累积量的NLOS误差识别算法[8]等。除上所述方法，基于不同的思想，国内外学者提出了很多富有意义的NLOS定位算法。文献[9]提出了一种具有鲁棒性质的移动目标定位算法，该算法利用测量样本的概率密度函数估计与有偏卡尔曼滤波算法实现NLOS环境下的移动目标定位计算。文献[10]提出利用NLOS误差分布及其参数己知这一先验知识，通过计算得出测量值中所包含的NLOS误差大小从而实现对NLOS距离测量值的校正。文献[11]提出利用残差检验鉴别出NLOS测量值，然后利用LOS距离测量值完成定位计算。文献[12]提出了一种线性规划算法削弱NLOS误差对定位的影响。文献[13]利用定位基站的几何关系，提出了一种具有约束条件的非线性最优化算法解决NLOS定位问题。文献[14]将LOS环境下的定位问题视为无约束的最优化问题，并将NLOS环境下的定位问题转化为具有约束条件的最优化问题并进行求解，在NLOS环境下具有较好的定位精度。文献[15]提出了一种基于半定规划的非视距定位算法，该算法利用半定规划转换方法，将NLOS环境下的定位问题转化为凸优化问题从而进行求解。H. Chen提出应用交互式多模型对LOS或者NLOS距离测量值进行交互滤波，之后便可应用经典定位算法对目标进行定位。上述方法虽然能有效识别NLOS节点，但是缺乏实时性。相较于上述方法，本文提出的基于改进多项式拟合的NLOS识别算法可以实时检测出NLOS节点，自适应的调整NLOS节点的判决门槛，提高NLOS节点的识别率。

1 基于多项式拟合的NLOS识别算法

无线传感器网络基本定位方法主要包括：基于到达时间（TOA）的定位方法、基于到达时间差（TDOA）的定位方法、基于方位角（AOA）定位方法和混合定位方法。基于TOA的定位方法原理简单，故该定位方法是目前基于网络定位应用最广泛的定位方法。

1.1 TOA测距模型

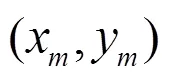
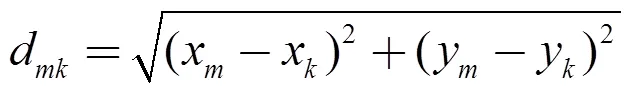
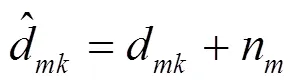
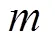
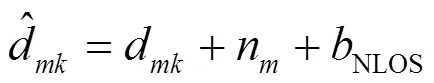
1.2 基于多项式拟合的NLOS识别算法

文献[17]中NLOS检测通过二次多项式拟合实现，该二次多项式拟合基于当前测量时间对最后个历史测量数据执行。然后，通过从先前的多项式拟合得到的曲线获得移动节点的距离预测，如图1所示。从预测值和下一个测量时间的距离测量获得残差。最后，将残差用作标识信标节点与移动节点之间的信号传播条件是LOS还是NLOS的阈值。但是多项式拟合基于最小二乘算法原理，容易受异常值影响，所以本文提出了基于改进的多项式拟合的NLOS识别算法。

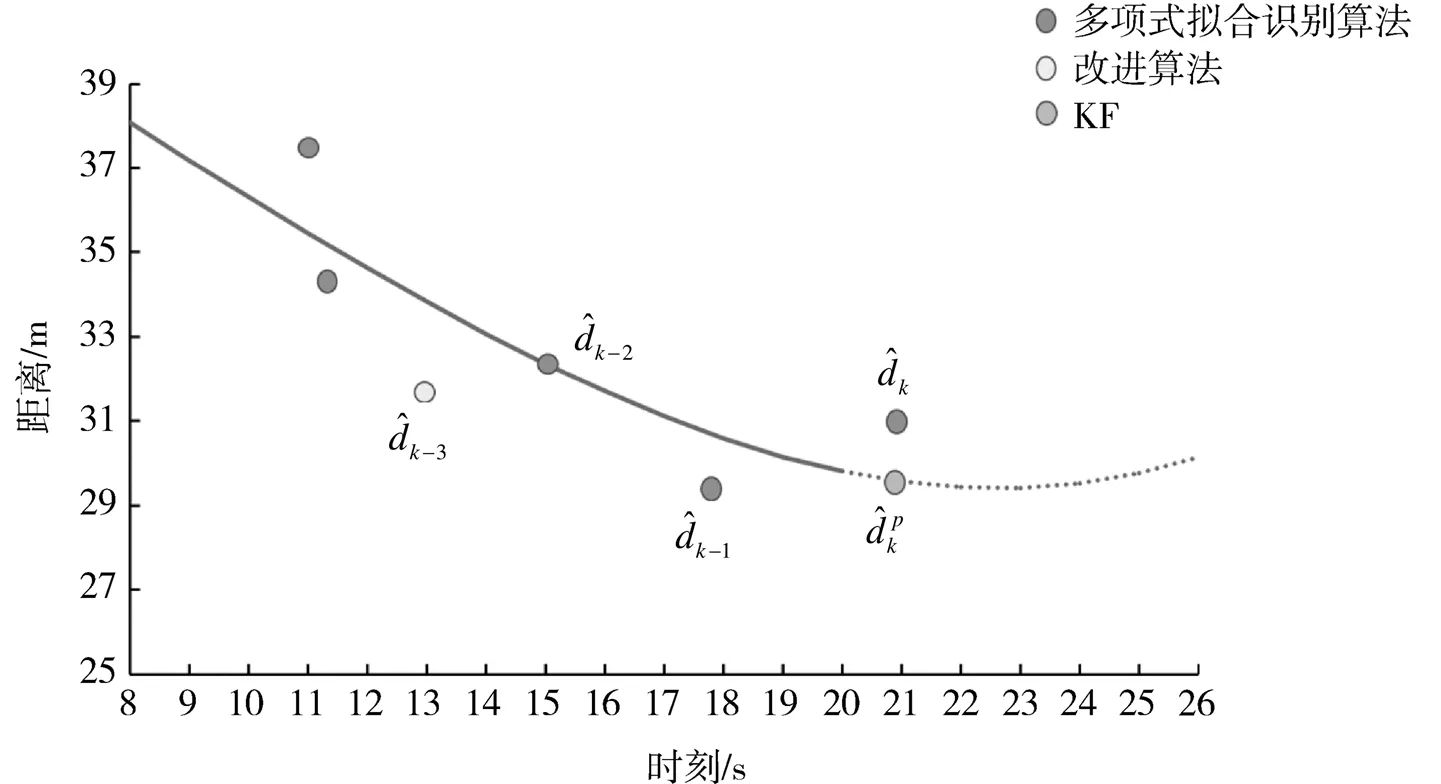
图1 多项式拟合示意图

2 基于改进的多项式拟合的NLOS识别算法

基于改进的多项式拟合的NLOS识别算法原理主要包括3个部分：①NLOS节点的识别；②NLOS节点的抑制；③最小二乘定位算法。

2.1 NLOS识别算法原理

NLOS识别的目的是判断测量数据是否受到NLOS传播的影响，即信号传播是否为NLOS传播，以便进行下一步处理。

基于改进的多项式拟合的NLOS识别算法的一次循环流程图如图2所示。

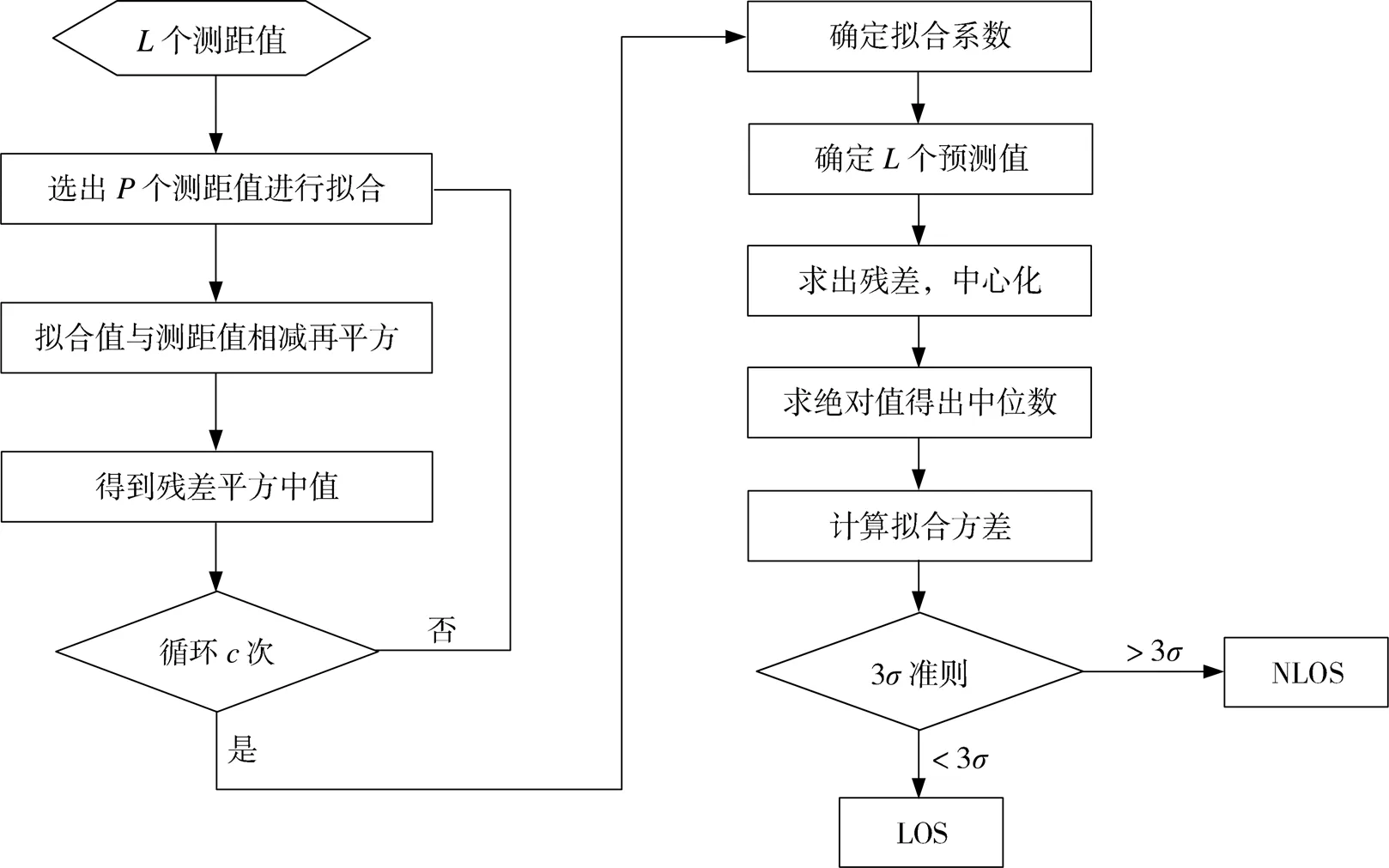
图2 算法流程图

在本文将NLOS误差视为异常值。

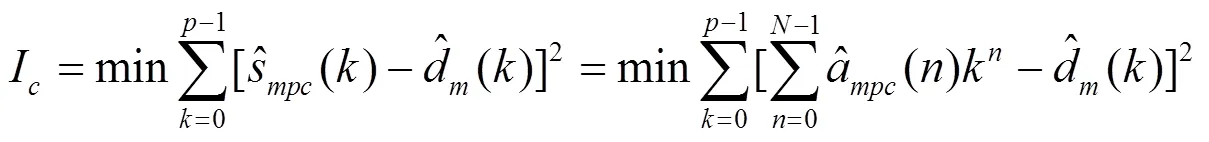
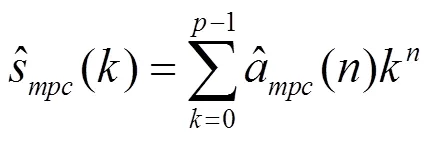
其具体步骤如下：

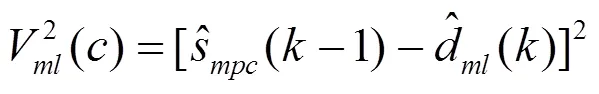
基于以上方法求出多项式系数之后，可以使用中位数法找到异常值，从而识别NLOS路径。步骤如下：

2.2 NLOS抑制算法原理

通过NLOS识别算法判别是否是NLOS节点，如果该节点是LOS节点，则将该测距值进行卡尔曼滤波处理，得到滤波后的值为NLOS抑制算法的输出值；如果该节点是NLOS节点，则将该测距值进行卡尔曼滤波处理，然后将通过多项式预测的测距值与卡尔曼滤波后的测距值加权，加权后的预测值即为NLOS抑制算法的输出。

2.2.1 基于卡尔曼滤波的数据处理

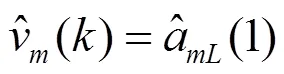
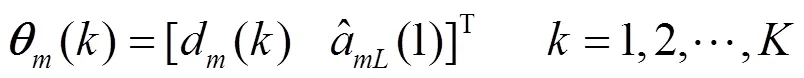
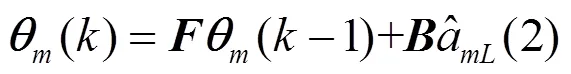
卡尔曼滤波可以总结为：

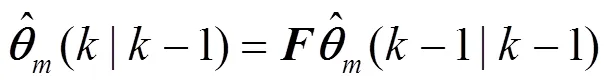
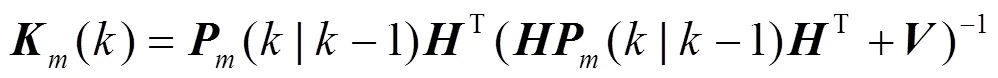
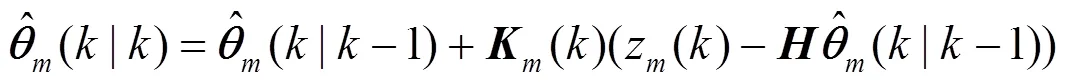
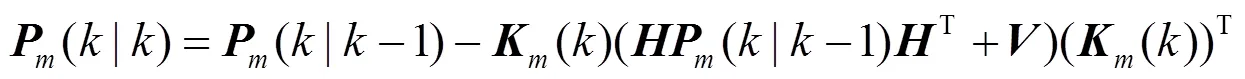
2.2.2 加权重构测距值

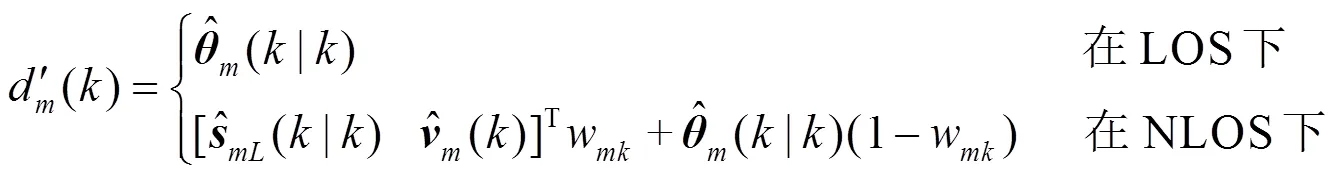
2.3 最小二乘定位算法

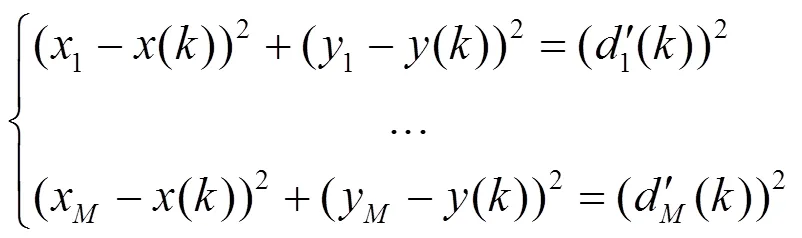
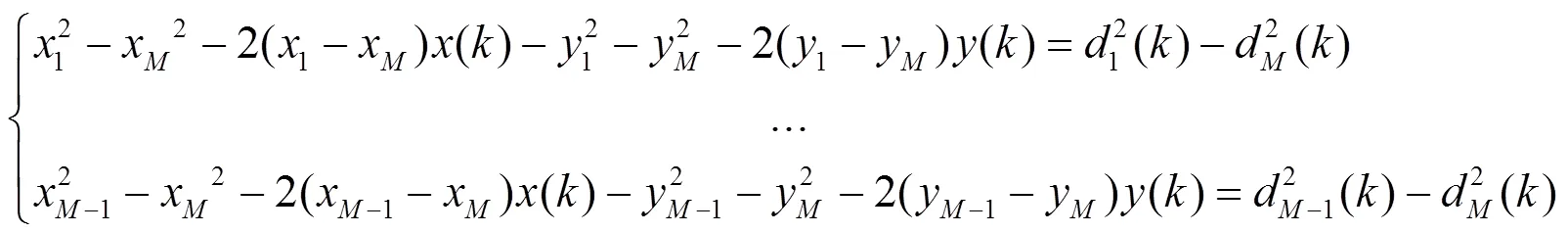
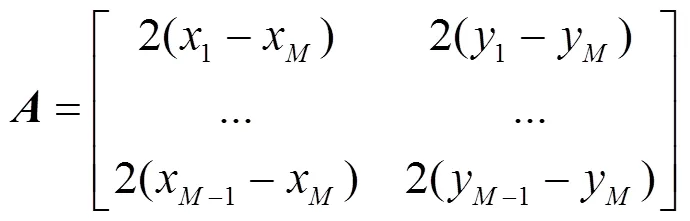
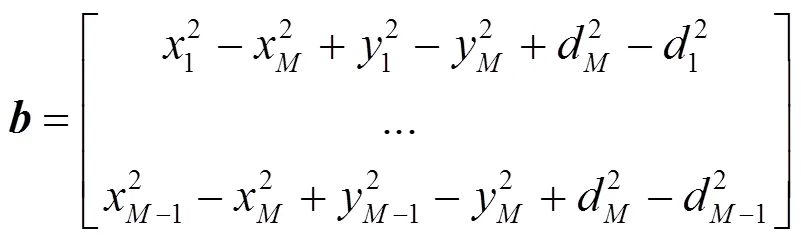
3 仿真结果

整体算法的流程图如图3所示。首先利用多项式拟合鉴别测量值中的非视距误差并且预测距离，通过拟合曲线和测量值之间的偏差来识别非视距误差，检测阈值可以根据测量值自适应的调整。然后利用卡尔曼滤波器处理测量值，在非视距传播下，对测量值进行加权重构。按照图3所示的流程进行仿真实验。

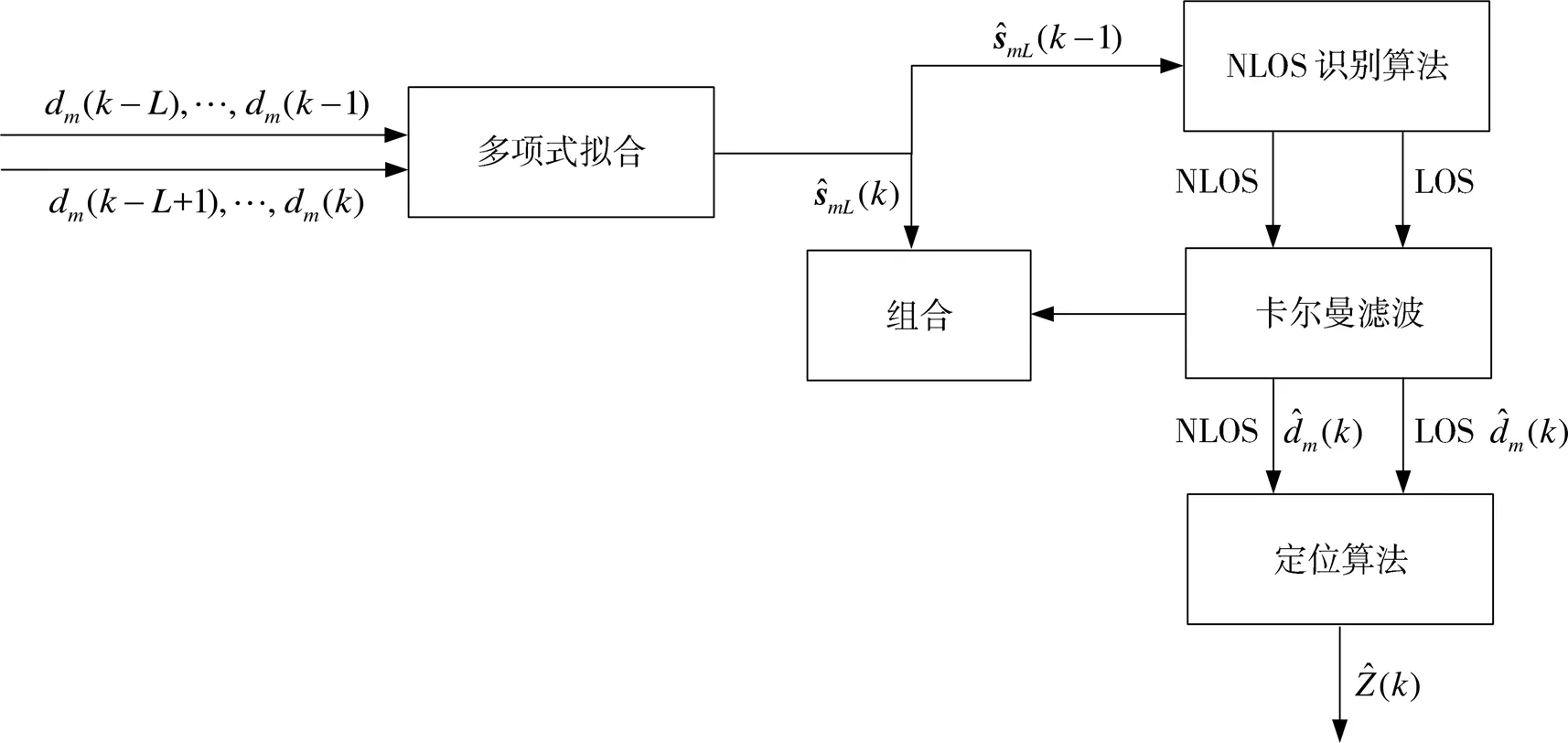
图3 整体算法流程图

将信标节点随机部署在120×100m的正方形空间中，并以NLOS概率随机生成移动节点与信标节点之间的传播条件。在仿真中，每次执行1 000次蒙特卡洛操作时，只有一个参数以固定的增量变化，其他参数保持默认值。均方根误差（RMSE）被认为是衡量算法好坏的性能指标，从得到的定位结果出发，间接衡量了NLOS误差识别算法的性能。由

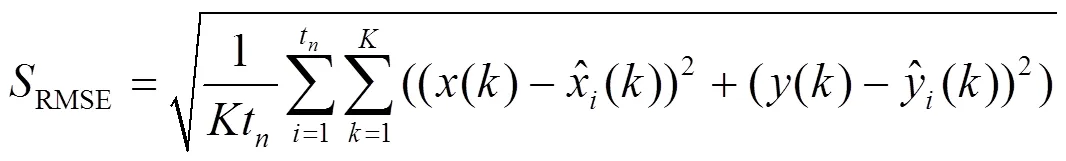
表1 参数表

按照表1所示的参数值，信标节点的个数为6个，位置分布如图4所示。在仿真实验中，随机加入NLOS误差，对一个信标节点而言，NLOS节点的个数为采样点数乘以NLOS节点比率，NLOS误差的分布如表1所示。图4为移动节点在时刻的真实位置即没有测量噪声和NLOS误差。在每次模拟中，移动节点的轨迹是固定的。

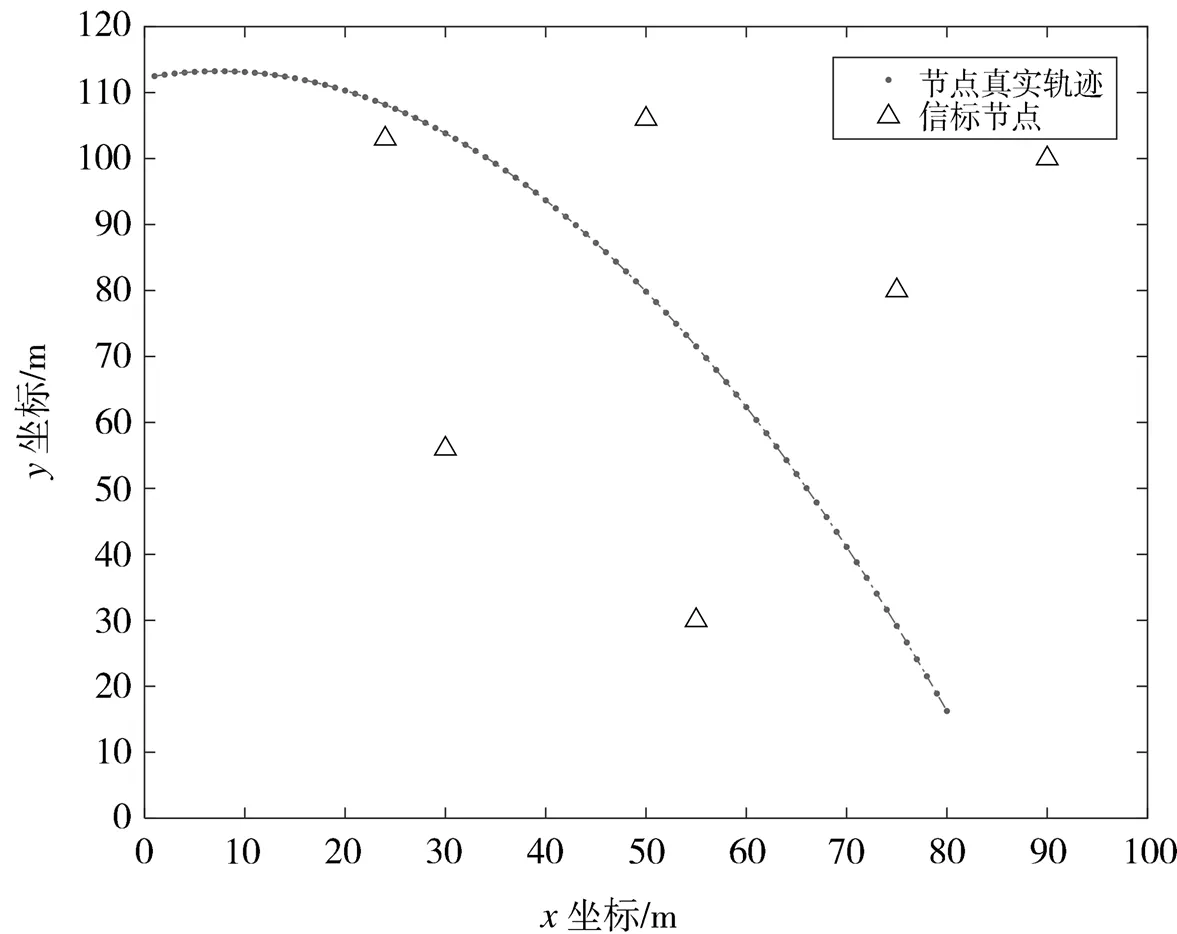
图4 移动节点的真实轨迹及信标节点

3.1 仿真结果

通过图5可以看出，由于改进算法NLOS误差的判决门槛的动态变化，可以发现提高了NLOS节点的识别率。

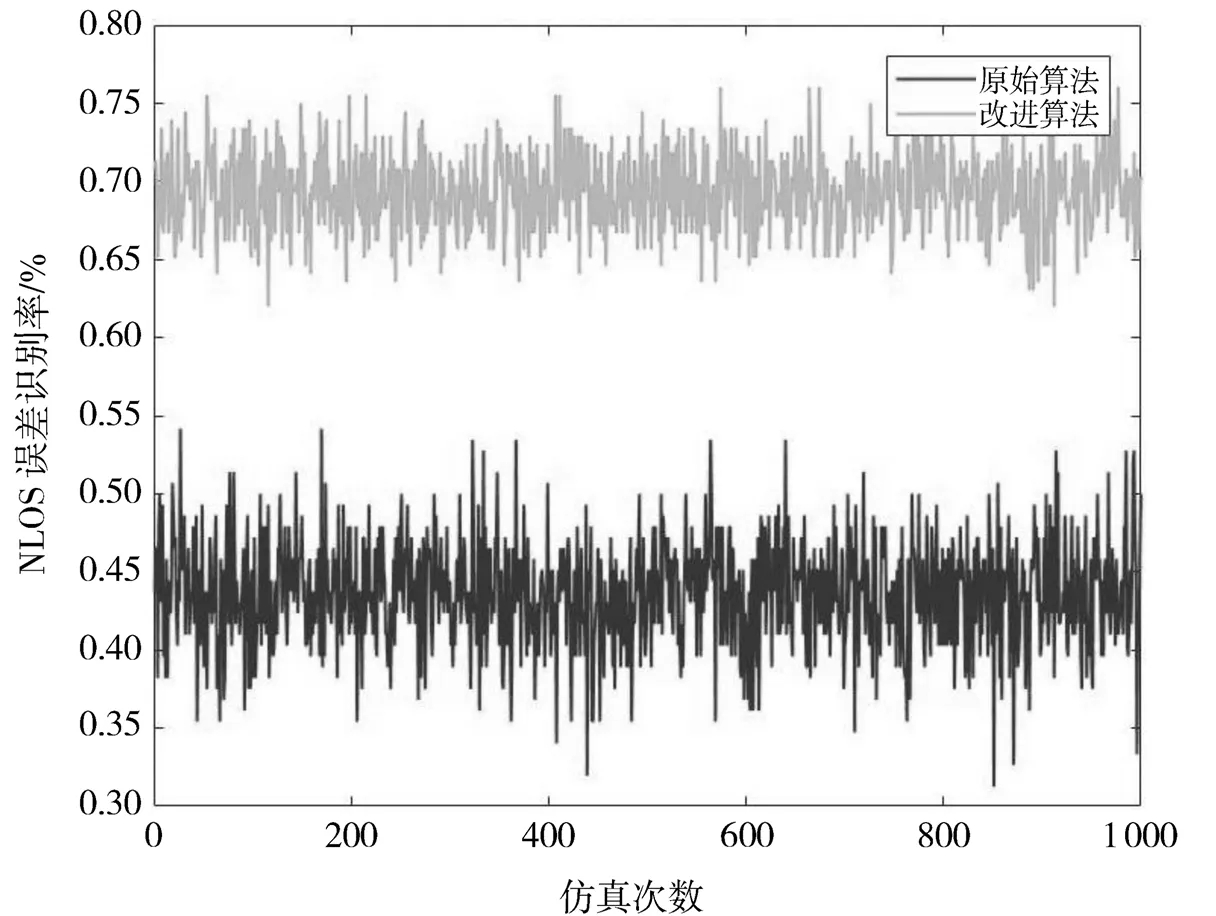
图5 NLOS误差识别率

与文献[16]相比，本文算法仅仅改变了NLOS误差识别算法，通过RMSE数值间接判断NLOS误差识别算法的性能，因此从下面几个图表中就可以得出改进的NLOS误差识别算法的性能。

按照表1的参数设置，固定其他参数，变化信标节点的个数，从而得到图6。

图6表示信标节点数量与RMSE的关系。随着信标节点个数的增加，所得到的测量值增多，可利用的信息增多，因此定位精度提高，从而RMSE逐渐减小。从图6可以看出与卡尔曼滤波算法和基于多项式拟合的NLOS识别算法相比，本文提出的识别算法有较好的性能，较于前两个算法来说提升了13.65%。

图6 RMSE（均方根误差）随信标节点变化

图7表示NLOS节点数量与RMSE的关系。由图7可知，随着NLOS节点比率的增大即非视距测量值的个数增多，因此影响多项式拟合的系数，造成预测的测距值误差增大，从而影响NLOS误差的识别率以及定位结果，按照公式（20）所示，文献[16]和本文的算法的RMSE逐步增大。文献[16]采用的是对所有历史时刻的距离进行拟合，而本文采用的算法是对部分历史时刻的距离进行拟合，当NLOS节点比率为0.1和0.2时，测量距离受NLOS误差影响不大，采用本文的算法就会丢失一些距离信息，从而导致算法性能比文献[16]差。

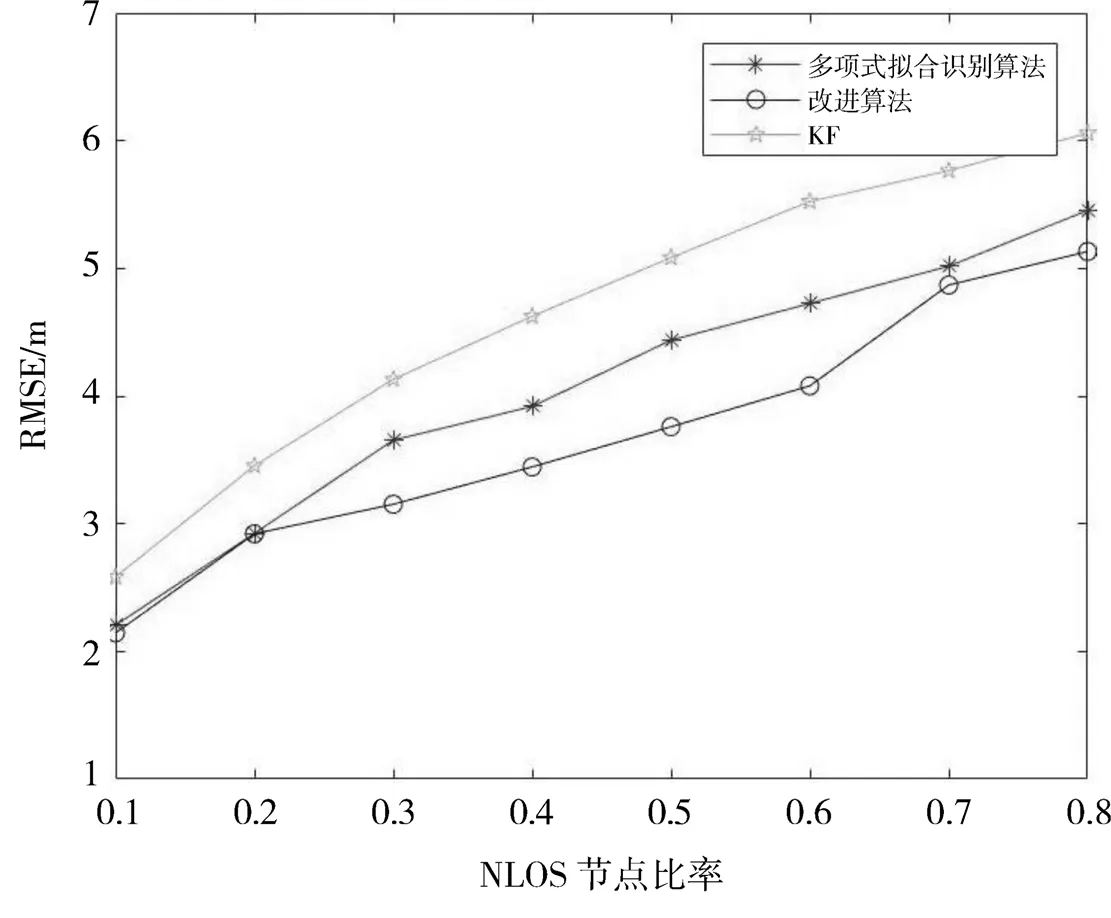
图7 RMSE（均方根误差）随NLOS比率变化

图8表示NLOS误差均值与RMSE的关系。随着NLOS误差均值的增加，非视距测距值误差增大，因此影响多项式拟合的系数，造成预测的测距值误差增大，从而影响NLOS误差的识别率以及定位结果。与卡尔曼滤波算法和基于多项式拟合的NLOS识别算法相比，本文提出的算法自适应的变换NLOS节点的判决门槛，对NLOS误差有较高的识别率，算法性能提升了10.34%。

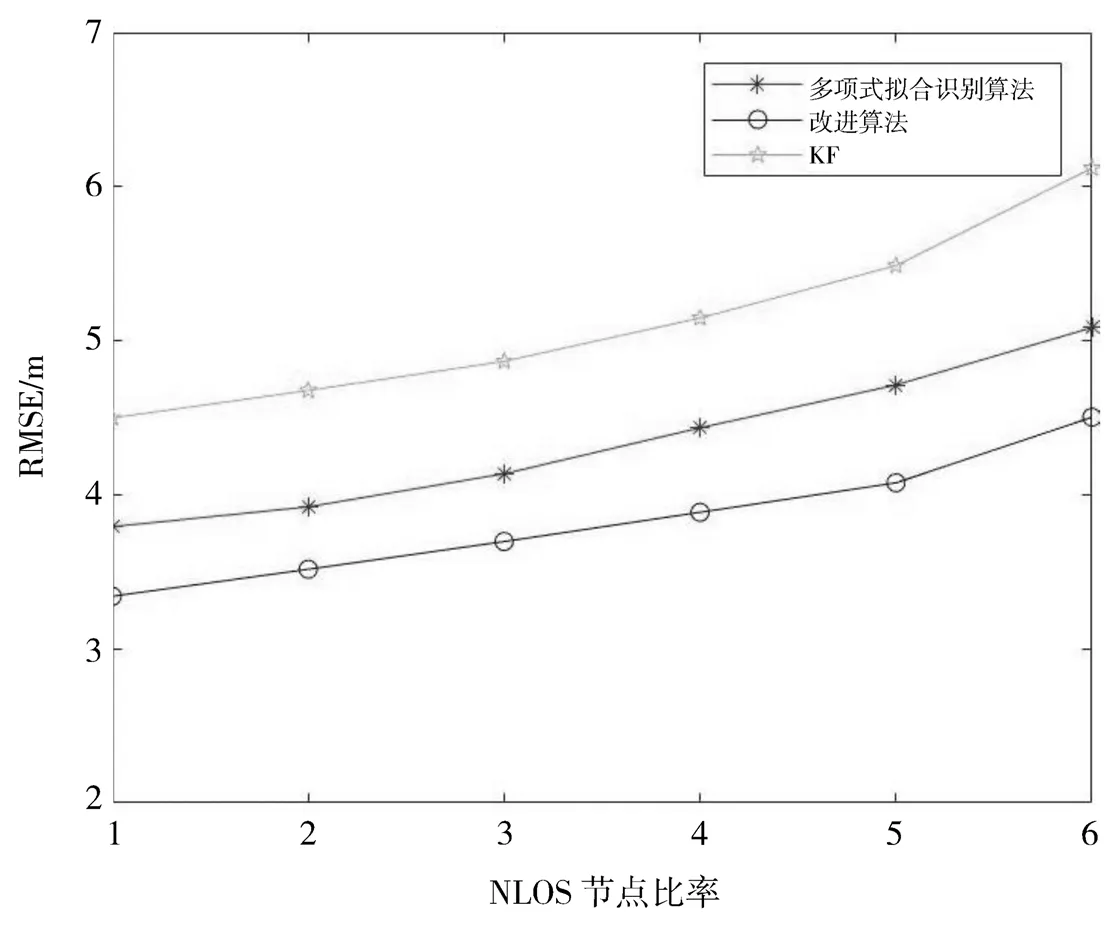
图8 RMSE（均方根误差）随NLOS误差均值变化

图9表示NLOS误差标准差与RMSE的关系。随着NLOS误差标准差的增加，非视距误差越大，造成非视距测距值误差增大，因此影响多项式拟合的系数，造成预测的测距值误差增大，从而影响NLOS误差的识别率以及定位结果。与卡尔曼滤波算法和基于多项式拟合的NLOS识别算法相比，本文提出的算法能够更有效地识别NLOS节点，较基于多项式拟合的NLOS识别算法提升了8.18%。

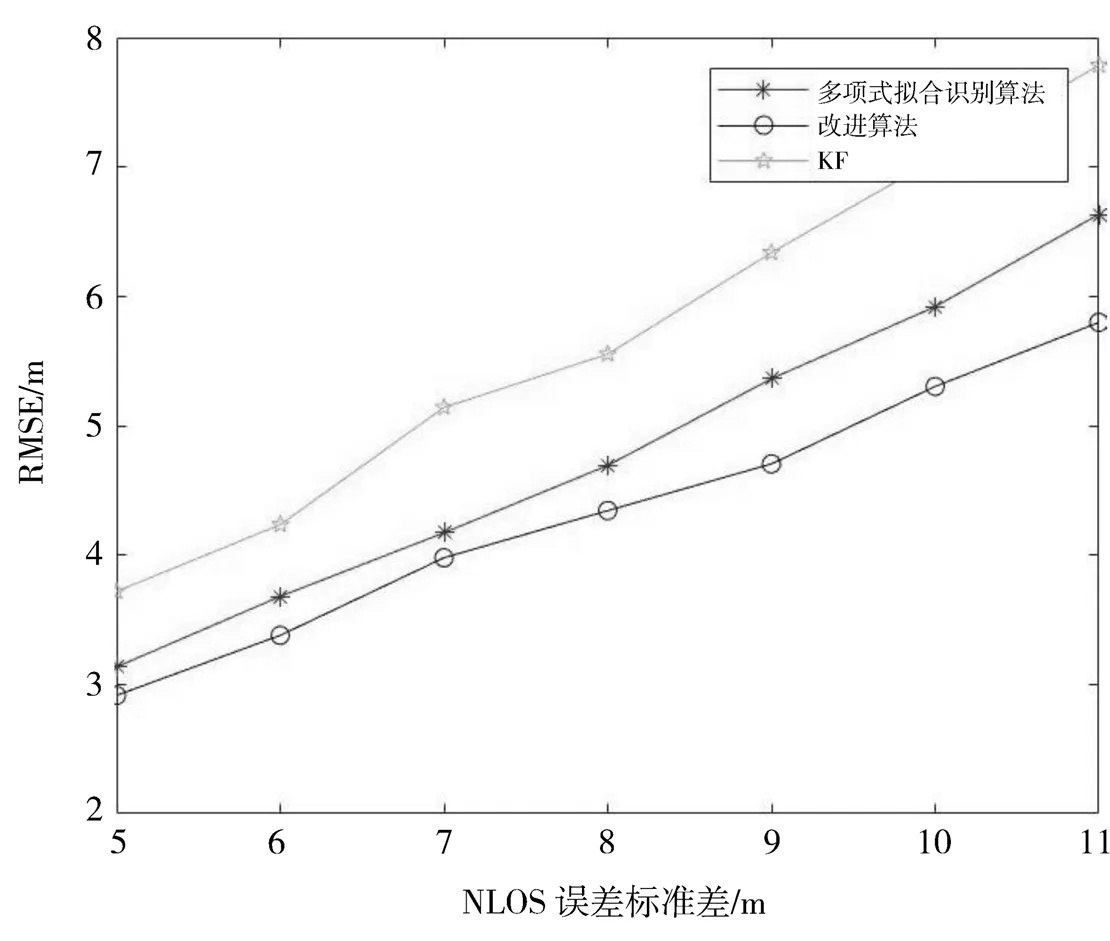
图9 RMSE（均方根误差）随NLOS误差标准差变化

4 结语

多项式拟合的NLOS识别算法基于最小二乘算法原理，容易受异常值影响，对后续预测值产生影响；NLOS节点的判决门槛固定，导致NLOS节点的识别率低。本文提出了一种能有效识别NLOS误差的多项式拟合改进算法，利用部分历史时刻的测距值进行多项式拟合来预测测量距离，有效地降低异常值对预测模型的影响；利用中值与方差的线性关系，自适应调整NLOS节点判决门槛，提高了NLOS误差的识别率。仿真结果表明，在NLOS误差严重的环境下，本算法性能较基于多项式拟合的NLOS识别的算法有所提升。

[1] AMUNDSON I, KOUTSOUKOS X D. A survey on localization for mobile wireless sensor networks[J]. MELT 2009: Mobile Entity Localization and Tracking in GOS Less Environments, 2009: 235-254.

[2] CAFFERY J J. A new approach to the geometry of TOA location[J]. IEEE Vehicular Technology Conference, 2000, 52(4): 1943-1949.

[3] 赵泰洋, 郭成安, 金明录. 一种基于RFID原理的交通信息获取系统与车辆定位方法[J]. 电子与信息学报, 2010, 32(11): 2612-2617.

[4] 田孝华, 廖桂生. 一种有效减小非视距传播影响的TOA定位方法[J]. 电子学报, 2003, 31(9): 1429-1432.

[5] WYLIE M P, HOLTZMAN J. The non-line of sight problem in mobile location estimation[C]//Proceedings of ICUPC-5th International Conference on Universal Personal Communications, Cambridge: IEEE, 1996(2): 827-831.

[6] CONG L, ZHUANG W H. Non-line-of-sight error mitigation in TDOA mobile location[C]//GLOBECOM'01. IEEE Global Telecommunications Conference, San Antonio: IEEE, 2001(1): 680-684.

[7] BORRAS J, HATRACK P, MANDAYAM N B. Decision theoretic framework for NLOS identification[C]//VTC'98 48th IEEE Vehicular Technology Conference, Ottawa: IEEE, 1998(2): 1583-1587.

[8] 王建辉, 胡捍英, 任修坤. 基于三阶累积量的NLOS误差抑制算法及其在WCDMA系统中的测试[J]. 信息工程大学学报, 2011, 12(4): 409-413+421.

[9] WANG J H, LI L C, HU H Y. A new approach for cellular wireless location in NLOS situations[C]//2006 First International Conference on Communications and Networking in China, Beijing: IEEE, 2006: 1-5.

[10] MAZUELAS S, LAGO F A, BLAS J. Prior NLOS measurement correction for positioning in cellular wireless networks[J]. IEEE Transactions on Vehicular Technology, 2009, 58(5): 2585-2591.

[11] CHAN Y T, TSUI W Y, SO H C, et al. Time-of-arrival based localization under NLOS conditions[J]. IEEE Transactions on Vehicular Technology, 2006, 55(1): 17-24.

[12] VENKAT S, BUEHRER R M. A linear programming approach to NLOS error mitigation in sensor networks[C]//2006 5th International Conference on Information Processing in Sensor Networks, Nashville: IEEE, 2006: 301-308.

[13] VENKATRAMAN S, CAFFERY J, YOU H R. A novel ToA location algorithm using LoS range estimation for NLoS environments[J]. IEEE Transactions on Vehicular Technology, 2004, 53(5): 1515-1524.

[14] WANG X, WANG Z X, O'DEA B. A TOA-based location algorithm reducing the errors due to non-line-of-sight(NLOS) propagation[J]. IEEE Transactions on Vehicular Technology, 2003, 52(1): 112-116.

[15] CHEN H, WANG G, WANG Z, et al. Non-line-of-sight node localization based on semi-definite programming in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2012, 11(1): 108-116.

[16] WANG Y, YAN Y, LI Z J, et al. A mobile localization method in smart indoor environment using polynomial fitting for wireless sensor network[J]. Journal of Sensors, 2020: 1-17.

[17] 蔡利栋, 傅瑜. 稳健的孤立点检测—从中位数求方差[C]//中国计算机学会理论计算机科学专业委员会, 长春: 2006年全国理论计算机科学学术年会, 2006: 185-187.

Non-line-of-sight error recognition algorithm based on improved polynomial fitting in indoor wireless positioning

ZHU Wen-ting1,2,3, ZOU De-cai1,3,4, YIN Ting1,2,3

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101048, China;3. Key Laboratory of Precise Positioning and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China;4. School of Astronomy and Space Science, University of Chinese Academy of Sciences, Beijing 101048, China)

Since the Global Navigation Satellite System cannot solve the positioning problem in indoor scene, indoor positioning technology arises at the historic moment. UWB, WiFi, etc indoor positioning technologies are widely used in various fields. Although they can meet the requirements of indoor positioning during line of sight propagation, the non-line-of-sight (NLOS) error caused by obstacles such as walls brings a sharp drop in positioning performance, and the accuracy cannot meet the needs of indoor positioning. In order to alleviate NLOS error and solve the problem of low recognition rate of existing algorithms, this study proposes an improved polynomial fitting algorithm of NLOS error recognition. Firstly, the method employs polynomial fitting to accomplish both NLOS identification and distance prediction. NLOS is identified via deviation between fitted curve and measurements. Detection threshold can be adjusted adaptively according to measurements. Then, it processes the measurements with a Kalman filter (KF), conducting weighting filter in the case of NLOS condition. The experimental results show that the method with low complexity performance in NLOS and the root mean square error improves 13.65% compared with the traditional polynomial fitting approach, and effectively suppresses the NLOS error.

indoor positioning; non-line-of-sight error recognition; polynomial fitting; Kalman filter

10.13875/j.issn.1674-0637.2021-01-0055-11

朱雯婷，邹德财，尹婷. 室内无线定位场景下改进多项式拟合的非视距误差识别算法[J]. 时间频率学报, 2021, 44(1): 55-65.

2020-07-14；

2020-09-16

载人航天创新性预研资助项目（17680601）