高速飞行器空气舵前缘三维烧蚀/温度耦合分析研究

杨凯威，梁 欢，赵小程，陈政伟，那 伟

（北京航天长征飞行器研究所，北京，100076）

0 引 言

空气舵是高速滑翔和再入机动飞行器的关键部件，其可提供飞行器控制力矩和升力，以此实现高速飞行器机动变轨和长时间在大气层内机动飞行。空气舵通常突出飞行器表面且结构形式复杂，当以高速、大攻角、大侧滑角在大气层内长时间飞行时，空气舵受到激波相互干扰，周围流场非常复杂，力、热环境恶劣，空气舵出现明显烧蚀，特别是舵前缘烧蚀更为严重[1]。空气舵前缘热防护问题突出，该问题一直是高速再入机动飞行器热防护设计的关键点和难点[2]。而解决这一难点的关键之一是准确预测空气舵前缘三维烧蚀/温度场，只有准确预测了空气舵前缘烧蚀外形、烧蚀量变化规律及舵前缘各组成结构温度分布、温度变化规律，才能精确设计空气舵前缘防热结构，合理评价空气舵前缘防热结构可靠性，以及外形变化对飞行器气动特性影响等问题。美国Aerotherm公司在20世纪60年代，开发出了烧蚀热响应计算程序（Charring Material Thermal Response and Ablation Program，CMA)，实现了烧蚀表面能量平衡方程与内部能量平衡及热解方程之间的耦合。然而，CMA程序在热解计算中采用的是显式算法，在计算收敛性和稳定性上有所欠缺[3]。Chen[4]等又将该程序应用到简单三维外形中，在稳定性和准确性方面有所提升，但该方法只能采用正交性良好的结构网格，不能很好地处理结构复杂的外形。2012 年，John A.Dec[5]利用有限元方法发展了系统的针对烧蚀材料内部多维热响应问题的分析程序，此程序采用高阶曲网格，大大增加了算法对多维曲边外形的适应能力。2015年，Alexandre Martin[6]等尝试在一维条件下高超声速热烧蚀非平衡流和材料热响应之间的紧耦合，并在一些简单的案例中对算法进行了验证。2018年，Wang[7]等应用用户子程序对一维条件下材料的热烧蚀效应进行了预测。张涛[8]等研究了二维条件下热解型碳化复合材料的烧蚀计算模型和计算方法，获得了热解气体质量流量分布。杨德军[9]等对碳/碳复合材料平头柱体模型的瞬态温度场进行了分析计算。2016年，刘骁[10]等对热防护系统三维有限元计算方法进行了研究，其求解方法还需要通过试验进行进一步验证与确认。针对空气舵前缘三维烧蚀温度场耦合分析的研究尚未见报道。

本文基于高速气动热力学、传热传质学、烧蚀理论等，采用自编烧蚀移动用户子程序代码方式，二次开发Abaqus有限元软件，利用二次开发软件仿真分析试验条件下空气舵前缘三维烧蚀/温度场，给出空气舵前缘不同时刻烧蚀外形、烧蚀量和三维温度分布，理论计算结果和试验结果进行对比的结果表明理论计算和实测结果吻合较好，验证了方法的合理性和正确性。

1 控制方程和数值模型

空气舵再入大气层飞行时，舵前缘外表面受到强烈气动加热，气体动能转化为热能，热流通过空气舵前缘表面进入结构内部，从而引起结构内温度场变化，空气舵前缘结构传热过程遵循三维热传导微分方程为

式中ρ为材料密度；Cp为材料比热；T为温度；t为时间坐标；xλ，yλ，zλ分别为x、y、z方向的导热系数；Q为内热源。

温度场控制方程可从泛函变分求得，也可从导热微分方程出发用加权余量法求得。加权余量法中更多采用的是伽辽金法（Calerkin）。假定空气舵内部无热源，物性参数各向同性，初始温度均匀。将空气舵前缘温度场计算域V离散为若干个单元，n个节点，对 式（1）加权积分得：

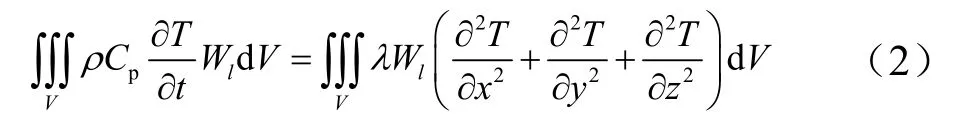
式中Wl为权函数，

对式（2）应用高斯公式整理后可得：

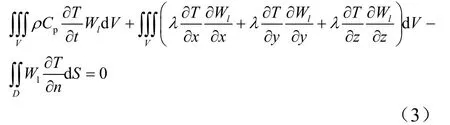
式中D为计算面积区域；S为边界面积；为温度在n方向上的导数。

烧蚀计算一般取六面体单元，对于单元E内任意点的温度T（x,y,z）用插值函数表示：

式中N1～N8为形函数；Te～Tm为单元E节点温度，对式（4）求导可知：

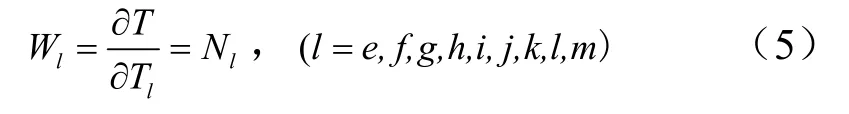
将式（5）代入式（3）式并考虑热流和辐射边界整理可得：

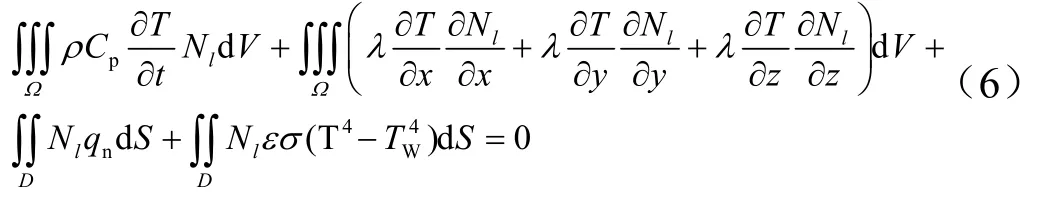
式中qn为壁面净热流；ε为辐射系数；σ为斯蒂芬-波尔兹曼常数；TW为表面温度。

式（6）为三重积分，在笛卡尔坐标系中进行三重积分，通常采用坐标变换的方法进行，即将笛卡尔坐标系转化为局部坐标系（ξ,,ηζ），即可将笛卡尔坐标内形状不规则单元转化为局部坐标系内形状规则单元，从而使得积分运算变得简化。首先引入坐标变换：

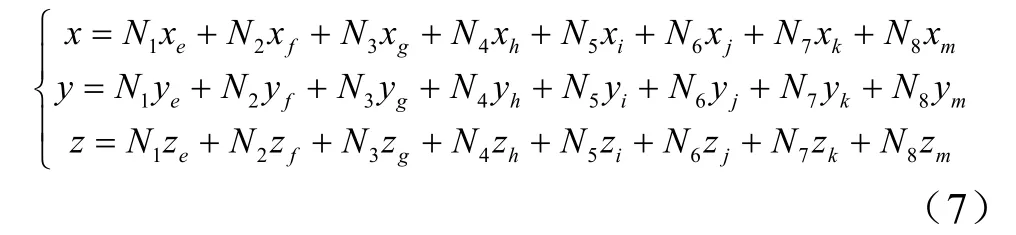
在自然坐标系下，式中的型函数须满足：

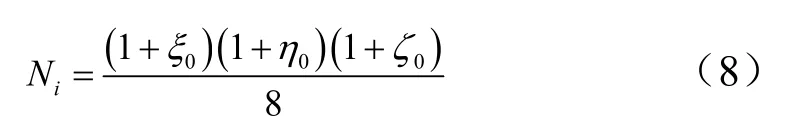
式中ξi、ηi、ζi为局部坐标系的节点坐标，其中，ξ0=ξiξ，η0=ηηi，ζ0=ζiζ。

对式（4）、式（7）求偏导数，将式（8）代入可得式（9）、式（10）。

式中J为雅克比（Jacobi）矩阵，其表达式为

对于体积微元、面积微元应用向量关系可得：

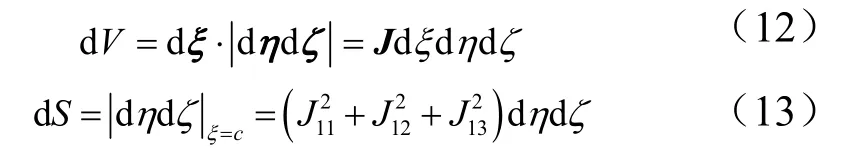
将式（9）～（10）、式（12）～（14）代入式（6），并将单元矩阵总体合成即可得到整个求解区域n个代数方程，将代数方程写为矩阵形式为

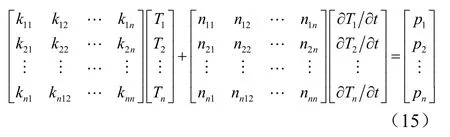
式（15）可简写为

式中K为温度刚度矩阵；T未知温度列向量；N为非稳态变温矩阵；P为边界载荷列向量；下标t表示这些列向量都取同一个t时刻的值。

对式（16）中｛∂T∂t｝t采用向后有限差分离散，整理后可得空气舵前缘三维温度场有限元方程：

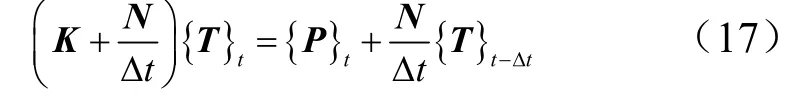
式中 ｛T｝t-Δt为初始温度场或前一时刻的温度场，为已知量，采用牛顿-拉普森（Newton-Raphson）迭代方法即可求得空气舵前缘各节点温度值。

2 三维烧蚀移动边界

2.1 烧蚀表面净热流边界条件

上述固体导热微分方程对于无烧蚀边界易于求解，但对于有烧蚀移动边界问题，求解就变得异常复杂。目前高速空气舵热防护通常采用烧蚀式热防护，防热材料大都为硅基类材料。该类材料通常以二氧化硅为主要成分按不同工艺方法与树脂复合而成，其烧蚀防热主要机理是依靠材料的质量损失和物理化学变化来消耗气动加热以达到防热目的。依据能量守恒条件可写出烧蚀条件下空气舵前缘表面净热流密度：

式中qN为净热流密度；为表面温度梯度；ψ为质 量引射系数；q0为不考虑壁面焓值影响的表面热流密度；hw为热壁焓；hr为恢复焓；ε为材料辐射系数；Tw为表面温度；v-∞为线烧蚀速率；ΔH为损失单位质量带走的热量（包括液态层流失、树脂分解热、SiO2蒸发吸热），其值可由试验获得。

对于式（18）中的q0可由式（19）获得：

式中qs为驻点热流密度；Rn为端头半径；为流态因子；ρ∞为来流密度；V∞为来流速度；rc为舵前缘半径；μ∞为气体粘度；Λ为舵前缘后掠角；m，a，b为常数，由试验获得。

对于hr有：

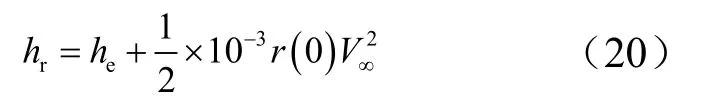
式中he为静焓；r（ 0）为恢复系数，为普朗特数。

ψ值可由下式获得：

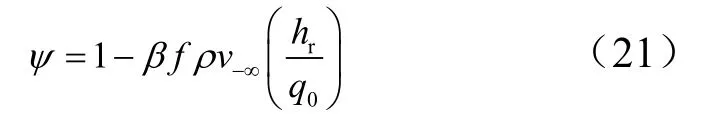
式中β为系数，层流下为0.62，湍流下为0.2；f为质量分数（包含树脂质量分数、SiO2质量分数）。

2.2 移动边界的烧蚀速率

通过式（18）可发现，要实现表面净热流密度加载，就需确定当前热环境条件下的烧蚀速度。目前计算硅类防热材料烧蚀速度方法主要是针对球-锥飞行器外形，而对于凸出飞行器表面的空气舵外形特别是空气舵前缘该方法已不适用。本文提出采用质量烧蚀速率与来流热流密度和压力关联式来计算烧蚀速度的方法[11]。选取空气舵前缘材料加工为驻点模型，试验设备采用电弧加热器，试验共进行了30余次，试验条件见表1。

表1 试验条件 Tab.1 Experimental Conditions

图1为对应状态下模型烧蚀后典型驻点形貌，可以看出，模型在表1条件下均发生烧蚀，低状态下模型表面的白色液态层少，较高状态下模型表面的液态层有所增加，高状态下除被气动剪切力吹掉的液态层外，大部分的白色液态层仍附着在模型表面。

图1 驻点烧蚀模型 Fig.1 Stagnation Ablation Model

根据表1测得的质量烧蚀速度与热流密度和压力的关系，采用多元回归的方法，得到硅基材料质量烧蚀速率与热流密度和压力的关联公式：

式中mt为质量烧蚀速度；k为常数；0P为压力。根据质量烧蚀速度和线烧蚀速度的关系，可得节点坐标的移动速度：

对烧蚀速度积分可得节点烧蚀移动量：

2.3 烧蚀/温度场耦合计算

当表面温度达到空气舵前缘材料烧蚀温度时，空气舵前缘发生烧蚀，其表面不断向后退缩，热量通过表面向内部传导，从而引起内部结构温升。烧蚀/温度场耦合计算的总体思路是：某一时刻表面温度达到材料烧蚀温度时，通过式（22）计算出材料烧蚀量，进而获得烧蚀带走的热量ρv-∞ΔH，通过式（24）可获得各节点烧蚀移动量，保持网格拓扑关系不变，运用网格移动技术，重新形成新外形，并采用插值方式将各节点温度信息插值到新外形节点上，再将新的热流边界加载至新外形上，重复上述步骤，即可实现各个时刻烧蚀/温度耦合计算。对于热流加载，本文开发了Abaqus有限元用户子程序 DFLUX，对于节点烧蚀移动量开发了用户子程序UMESHMOTION。由于烧蚀属于网格大变形问题，通过采用ALE（任意拉格朗日欧拉）网格技术，实现了烧蚀区域网格平顺变形。开发后的软件计算耦合条件下烧蚀/温度主要分为3步：a）读入热环境参数热流q0、恢复焓hr、壁面压力p；b）根据初始温度，利用DFLUX加载净热流边界计算出Tw以及空气舵前缘内部温度；c）用计算所得表面温度与烧蚀判别温度比较，通常硅基材料的烧蚀判别温度是指材料表面出现熔融液态层时的表面温度，不同的硅基材料烧蚀判别温度有所不同，应通过试验获得烧蚀判别温度。表面温度若小于烧蚀判别温度，温度场按式（18）中ρv-∞ΔH=0的qN加载计算；若大于烧蚀判别温度则完全按式（18）中的qN加载计算温度场。

3 方法验证

3.1 计算模型和条件

选取空气舵前缘局部建立有限元模型，如图2所示。舵前缘母线长度165 mm，高度60 mm，舵前缘后掠角Λ=68.7°，端头半径Rn=20 mm，舵前缘半径rc= 13 mm。计算模型为硅基复合材料，密度ρ=1670 kg/m3，导热系数λ=0.65 W/(m·K)，比烧蚀焓ΔH=45 kJ/kg，发射率ε=0.85，舵前缘热流密度q=16 208 kW/m2，焓值hr=5898 kJ/kg，压力p=0.7 MPa，计算时间为 8 s。

图2 舵前缘局部有限元模型 Fig.2 A Portion of Rudder Leading Edge Finite Element Model

3.2 计算与试验结果对比

图3为数值计算的空气舵前缘三维烧蚀温度云图。由图3可知，舵前缘最高温度达到2363 K，超过了硅基材料熔融温度，空气舵出现明显烧蚀，舵前缘网格出现后退，由于加载的热流较为均匀，所以沿前缘母线方向的烧蚀量变化也较为均匀。

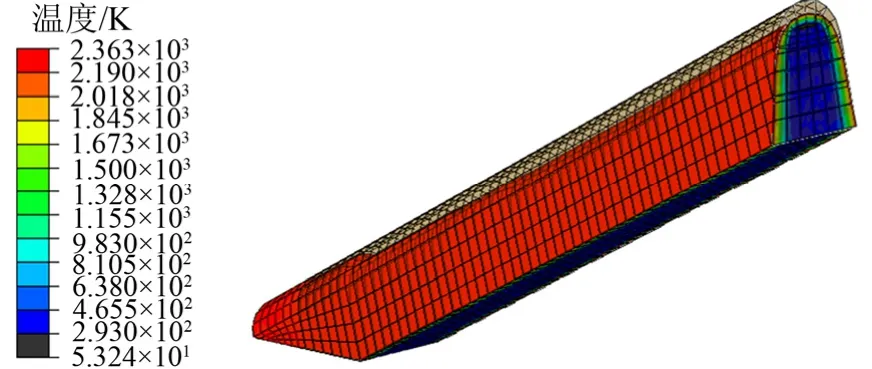
图3 舵前缘三维烧蚀温度云图Fig.3 Three-dimensional Ablation Temperature Contour of Rudder Leading Edge

为更好观察空气舵前缘烧蚀温度分布情况，沿舵前缘1/2位置处截取温度分布图，如图4所示。由图4可知，舵前缘和舵面温度均达到了材料烧蚀温度，发生烧蚀，前缘温度高于舵面温度，计算模型法线方向温度梯度最大，高温区均集中在烧蚀表面，主要是由于硅基材料热导率低。

图4 舵前缘截面温度云图Fig.4 Cross-sectional Temperature Contour of Rudder Leading Edge

图5为舵前缘1/2位置处烧蚀量截面云图。

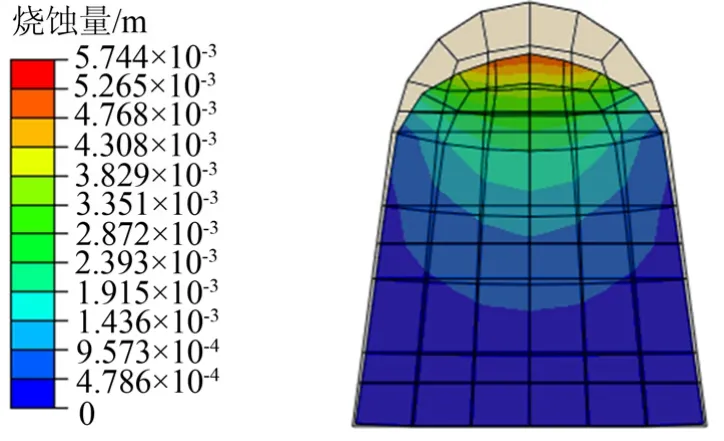
图5 舵前缘截面烧蚀云图Fig.5 Cross-sectional Ablation Contour of Rudder Leading Edge

由图5可知，舵前缘和舵面均出现烧蚀，烧蚀量沿前缘弧顶至舵面逐渐减小，前缘烧蚀量最大，为5.744 mm，位置在舵前缘圆弧顶点处，烧蚀后的舵前缘外形与初始外形相比，曲率半径变小，外形变平缓。

为验证方法的正确性，选取舵前缘局部模型（小三角），在电弧加热器上进行了前缘定态模拟烧蚀试验。模型材料与计算模型相同，试验模拟了计算热环境条件的100%。图6a为电弧加热器试验模型，试验采用矩形喷管，将试验模型通过工装固定在喷管前方；图6b为烧蚀后的舵前缘模型，从烧蚀试验后的模型可知，前缘圆弧与舵面接触处出现白色熔融液态层，表明舵前缘发生了严重烧蚀，烧蚀量沿母线方向较为均匀。试验过程利用红外点温仪测量了前缘表面温度，其值为2255 K。

图6 舵前缘局部烧蚀试验Fig.6 Ablation Test of Rudder Leading Edge

试验后测量了前缘法向烧蚀量，最大烧蚀量为5.39 mm（虚线为原始外形），试验测量结果和仿真计算结果的对比见表2。

表2 表面温度和烧蚀量仿真结果和试验值对比Tab.2 Comparision of Simulation Results and Experimental Values of Surface Temperature and Ablation

由表2可知，理论计算表面温度和烧蚀量均大于实测值，表面温度高出实测值108 K，理论值和实测值相对偏差为 4.79%，烧蚀量理论值高出实测值0.354 mm，理论值和实测值相对偏差为 6.56%，满足高速热防护设计烧失量计算偏差要求，一般要求 10%以内。

4 结 论

本文通过对高速空气舵前缘三维烧蚀/温度场耦合分析研究，可得如下结论：

a）基于通用有限元软件，采用二次开发自编热流密度加载和烧蚀移动边界用户子程序方法，可仿真分析空气舵前缘等复杂结构的三维烧蚀/温度场，为分析空气舵前缘热应力和评价空气舵前缘热结构设计合理性和可靠性提供了较为精细的理论分析方法；

b）提出用热流密度和压力关联式计算空气舵前缘烧蚀后退量工程方法，解决了后掠空气舵前缘烧蚀量计算和边界节点移动控制量问题，同时与ALE方法有机结合，可合理地给出复杂结构三维烧蚀外形；

c）通过舵前缘局部烧蚀试验可知，仿真结果和试验实测值较为接近，且仿真结果高于实测值，偏差小于10%，表明方法正确合理。