高考数学试卷与课程标准的一致性研究

张磊 梁芳

摘 要：文章以2019年高考数学全国Ⅰ卷、Ⅱ卷为研究对象，采用韦伯一致性分析模式分析试卷与课程标准一致性。研究表明，2019年高考数学全国Ⅰ卷、Ⅱ卷理科卷与课程标准的一致性和文科卷相同，适应未来高考文理不分科的形势，且不同地区适合使用相同的高考数学试题，数学卷整体质量较高，但知识广度与课程标准未达到一致性水平，在试卷编制过程中可以考虑细化与合理分配对各知识模块的考查。

关键词：高考改革;数学;课程标准;一致性

中图分类号：G633.6 文献标志码：A文章编号：1008-3561（2021）04-0060-04

高考试题与课程标准一致性研究备受关注，但国内研究多以评价试题质量与价值为主。随着一些地区已经实施高考综合改革，从试题与课程标准一致性分析的角度来探究试题是否适应高考文理合卷改革政策、能否顺应曾经使用不同试卷的地区在未来使用相同试题趋势这类问题的研究尚未出现。本文对 2019年高考数学全国Ⅰ卷（文科和理科）、高考数学全国Ⅱ卷（文科和理科）进行研究，研究工具选择韦伯一致性分析模式，剖析在各维度高考数学试题与课程标准能否达到一致性，试从一致性分析的角度探讨2019年高考数学全国Ⅰ卷、Ⅱ卷能否为未来高考文理不分科以及使用这两类试题的部分地区在未来使用相同高考试题的改革政策提供依据。

一、研究设计

1.研究对象

2019年高考数学全国Ⅰ卷（文科和理科）、高考数学全国Ⅱ卷（文科和理科）、《普通高中数学课程标准（实验）》。

2.研究工具

一致性分析模式是指判断、分析课程系统各个要素之间吻合程度的理念、程序与方法的总和。目前常见的一致性分析模式有韦伯模式、SEC模式、Achieve模式。我国不乏有学者运用其中某些模式分析试卷与课程标准的一致性，以考查试题价值，如王永强运用韦伯模式分析2015年高考数学试卷与课程标准的一致性，张蕾运用SEC模式分析2019年高考语文试题与课程标准的一致性，陈鹃娟运用Achieve模式分析2018年高考数学试题与课程标准的一致性。

本文的研究工具选择一致性分析模式的母体——韦伯分析模式。美国CCSSO曾指出，韦伯分析模式在剖析学业评价与课程标准关系的多种方式中是最重要且最具创造性的模式，并证明了其编码过程的可靠性，在分析试卷知识与技能方面有很高的適用性。

诺曼·韦伯主张要对课程内容标准要进行具体目标的描述，以构建学业评价与课程标准之间的一致性，从而生成形如“金字塔”的课程内容目标的层级体系。金字塔顶端最具概括性地描述了课程内容目标，即内容主题;金字塔的中间部分是单元目标，是内容主题下一级的目标;金字塔底端对应课程内容中最具操作性的目标，即具体目标。目标层级体系为一致性分析评价提供了基础。诺曼·韦伯从四个不同的维度考查试卷具体内容与课程标准的一致性，依次为“知识种类”“知识广度”“知识深度”“知识分布的平衡性”。

诺曼·韦伯认为，知识种类的一致性是用来判断测试题中涉及的学习内容与课程标准中要求考查的学习内容是否一致，当试卷中所涉及课程标准的内容主题的题目数量不少于6，在知识种类这一维度上，该内容主题达一致性。知识广度的一致性是用来判断测试题中所考察的内容范围与课程标准所要求掌握的内容跨度是否一致，当试卷击中目标数的百分比不小于50%，在知识广度这一维度上，该主题达一致性。知识深度的一致性是用来判断测试题中所考查到具体目标的认知深度水平是否符合课标要求的认知深度，符合具体目标认知深度的题目数量百分比不小于50%时，在知识深度这一维度上，该主题达一致性。知识分布的平衡性是用来判断测试题中考查的知识（具体目标）在课程标准中是否均匀分布，当知识分布平衡性指数不小于0.7，则认为在知识的分布平衡性这一维度上，该主题达一致性。平衡性指数计算公式为：平衡性指数=1-■。（O为该内容主题击中课标的具体目标总数，Ik为某一具体目标对应的题目总数，H为命中该内容主题的题目总数）

3.对研究对象编码统计

（1）对课程标准编码统计。我国高中数学涉及三大知识模块，每个知识模块分为不同的主题，每个主题下涵盖的各个知识点，可依次对应为“金字塔”课程内容目标体系的内容主题、单元目标及具体目标。高考数学全国Ⅰ卷、Ⅱ卷中考题的具体考查内容因考生而异，为非主干部分，本文暂不分析“坐标系与参数方程”“不等式选讲”这两个单元。2019数学考试大纲指出知识要求范围参照高中数学课程标准（实验版），笔者将课程标准的内容目标对应制为表1、表2。表1与表2有些单元目标名称虽然相同，但包含的具体目标有差异，有的是知识点存在差异，有的是知识深度水平存在差异。

（2）对高考数学试题编码统计。编码过程中，以每道题包含的具体目标为对象，若某题涉及2个具体目标，则记为2个题目。在对数学试题编码统计过程中，对每个题目的求解过程和步骤都加以分析，与课程标准的具体目标相对照，确定各题目对于相应具体目标考查所达到的深度水平，以及与课程标准要求的深度水平是否相符。

二、研究结果与数据分析

1.全国Ⅰ卷理科卷、文科卷与课程标准一致性分析

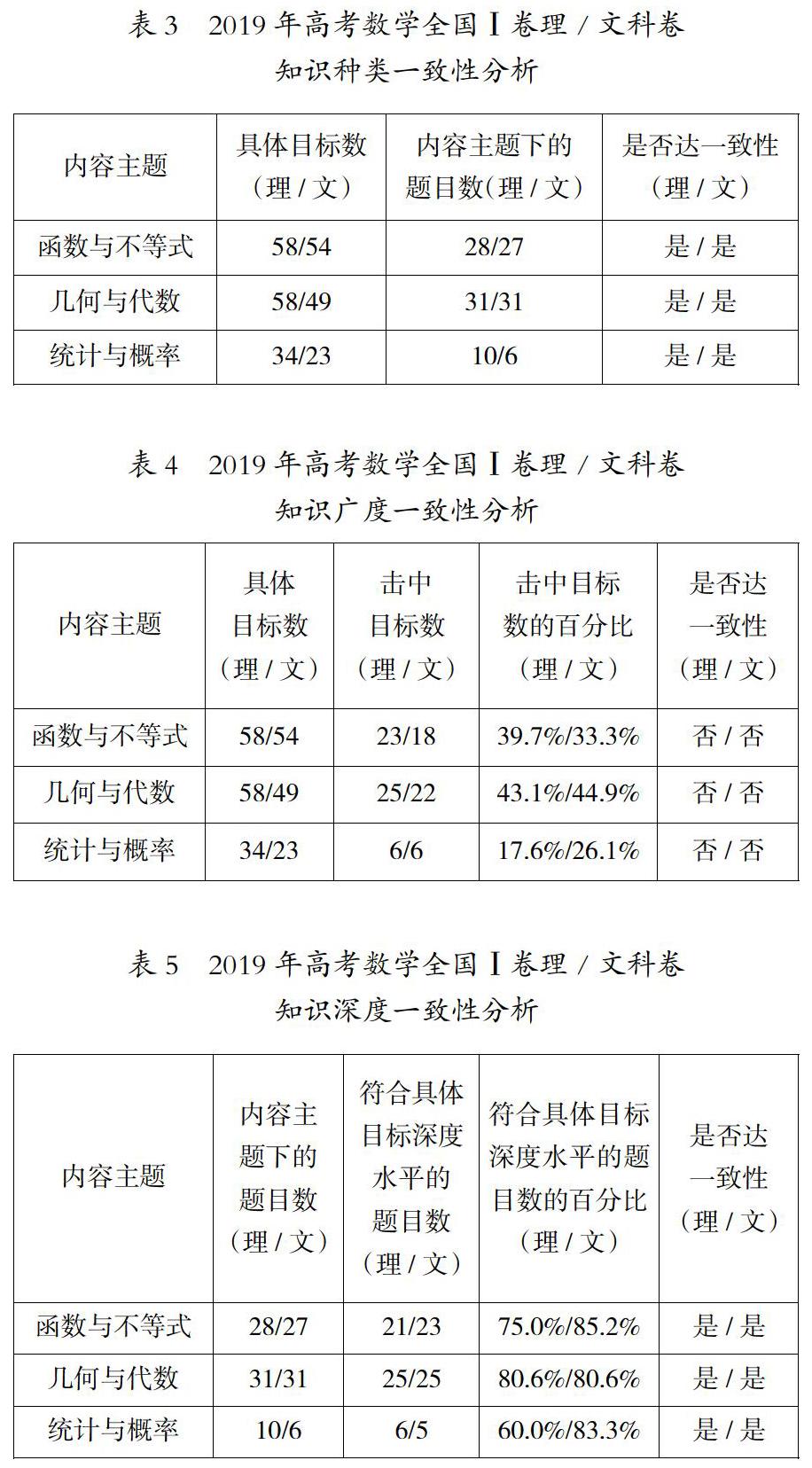
由表3～表6可知，在知识种类层面，理科卷与文科卷的一致性结果完全相同，3个内容主题与课程标准均达到一致;在知识广度层面，理科卷与文科卷的一致性结果相同，3个内容主题与课程标准均未达到一致;在知识深度层面，理科卷与文科卷的一致性结果完全相同，各内容主题与课程标准均达到较高一致性水平;在知识分布平衡性层面，理科卷与文科卷的一致性结果也完全相同，各内容主题与课程标准均达到较高一致性水平。因此，2019年高考数学全国Ⅰ卷理科卷与课程标准的一致性结果完全同于文科卷与课程标准的一致性结果。

2.全国Ⅱ卷理/文科卷与课程标准一致性分析

由表7～表10可知，在知识种类层面，理科卷与文科卷的一致性结果完全相同，3个内容主题与课程标准均达到一致;在知识广度层面，理科卷与文科卷的一致性结果相同，3个内容主题与课程标准均未达到一致;在知识深度层面，理科卷与文科卷的一致性结果完全相同，各内容主题与课程标准均达较高一致性水平;在知识分布平衡性层面，理科卷与文科卷的一致性结果也完全相同，各内容主题与课程标准均达较高一致性水平。因此，2019年高考数学全国Ⅱ卷理科卷与课程标准的一致性结果完全同于文科卷与课程标准的一致性结果。

三、结论与思考

第一，2019年全国Ⅰ卷、Ⅱ卷文理卷与课程标准一致性结果完全相同，适应未来高考文理不分科的形势。高考数学试卷由文理两卷合为一套试卷是高考综合改革内容之一。虽然文理科卷对个别内容主题下的具体目标要求不同，但2019年高考数学全国Ⅰ卷理科卷与课程标准的一致性结果完全同于文科卷与课程标准的一致性结果，说明文科卷和理科卷对于各个知识种类、知识广度、知识深度和知识分布平衡性的考查形式与程度存在很大的相似性。全国Ⅱ卷文理卷情况类似，对应课程标准的一致性分析也有相同的结果。因此，对于2019年高考数学全国Ⅰ卷、Ⅱ卷使用地区，高考数学由文理两卷整合为一套试卷的方案具有一定可行性。

第二，全国Ⅰ卷、Ⅱ卷与课程标准的一致性水平相同，在一定程度上适合不同地区使用相同的高考数学试题。对于全国Ⅰ卷、Ⅱ卷与课程标准的一致性分析结果呈现相同的一致性分布：在知识种类这一层面，都达到了一致性水平;在知识广度这一层面，所有试卷均未达一致;在知识深度与知识分布平衡性这两个层面，所有试卷与课程标准都达到了较高的一致性。通过对当前全国Ⅰ卷、Ⅱ卷与课程标准的一致性分析可知，未来可以在一定程度上在不同地区使用相同的高考数学试题。

第三，2019年全国Ⅰ卷、Ⅱ卷数学卷整体质量较高，但知识广度与课程标准未达到一致性水平，在试卷编制过程中可以考虑更加细化与合理地分配对于各知识模块内容的考查。根据全国Ⅰ卷、Ⅱ卷的文理卷与课程标准的一致性分析结果可知，在知识种类层面，各内容主题均达到一致性，因此试卷所考查的知识范围相对于课程标准较为适宜。知识深度与知识分布平衡性方面三个内容主题也都达到较高的一致性水平，试卷整体质量较高。然而，在知识广度层面，各高考数学试卷的所有内容主题与课程标准均未达到一致性水平，这可能是由于试卷编制可能存在某些题型分数占比偏高或题目类型相对单一的问题。因此，对于题目分数分配与试题类型尚存在改进的空间，对于各知识模块内容的考查可以更加细化与合理。以全国Ⅰ卷、Ⅱ卷为例，选择与填空题共计16题，每题5分，共计80分;解答题共计6题，必考题含5题，每题12分，选考题有1题，每题10分，共计70分。对于各题目分数分配，在难度适当的前提下，选填部分可适当减少每题分数而相应增加题目总数，解答题部分可在某些题目适量增加设问，也可考虑在此基础上适应性地调整客观题与主观题的分数分配比例，使对学生在知识广度层面的考查达到更高的效度;在试题类型方面，可考虑增加多选题等其他类型题目，在一题中考查更多的知识模块内容，从而在知识广度层面与课程标准达到更高的一致性水平，提高试卷质量。

参考文献：

[1]Norman L W. Alignment of Science and Mathematics Standards and Assessments in Four States[M].Washington D C：Council of Chief State School Officers，1999.

[2]王永强，韩洪芹.高中数学课程标准与数学高考试卷的一致性分析——基于韦伯分析模式的研究[J].教学研究，2016（05）.

[3]张蕾，刘聪.2019年全國高考语文试题与课程标准的一致性研究：基于SEC模式[J].教育测量与评价，2019（12）.

[4]陈鹃娟，周莹.基于Achieve模式的2018年全国高考数学试题与最新版课程标准一致性研究[J].教育测量与评价，2019（06）.

[5]Norman L W. Criteria for alignment of expectations and assessments in mathematics and science education[M].National Institute for Science Education University of Wisconsin-Madison，1997.

[6]Porter， A.C. and Smithson， J.L. Standards-based reform in The states Chicago： National Society for the study of Education[M]. Chicago： University of Chicago Press，2001.