基于线性相位近似的SOQPSK-TG信号同步算法*

王 乐，刘 靖

(北方工业大学 电子工程系，北京 100144)

0 引 言

成形偏移正交相移键控(Shaped Offset Quadrature Phase Shift Key,SOQPSK)信号是一种兼具连续相位调制(Continuous Phase Modulation,CPM)和OQPSK优点的调制方式[1]。该调制信号包络恒定的特性使得发射系统受功放非线性影响较小，在遥测系统、卫星通信和军事通信中都有广泛的应用[2-4]。SOQPSK-TG(Telemetry Group version of SOQPSK)是美国先进靶场下一代遥测系统推荐的调制方式[5]，该调制信号将用于今后遥测网络iNet标准中[6]。

同步是接收系统对收到的调制信号首先要完成的处理工作，决定了后续信号均衡、检测和解码等模块的性能，是信号解调首要解决的问题，其同步精度直接影响通信系统整体的性能。同步是对接收信号的载波频率偏移、载波相位误差(相干解调时需要此参数)和定时误差进行估计，然后用估计的结果补偿本地的载波和定时采样脉冲。由于SOQPSK-TG信号的特殊性，同步算法一般采用基于直接判决的反馈环结构实现，即相位误差和定时误差需要符号判决的信息辅助[7]。文献[8]推导了低复杂度的直接判决同步算法，理论上证明了算法的有效性。由于CPM信号符号判决的复杂性，文献[9]和文献[10]分别提出了基于脉冲幅度调制(Pulse Amplitude Modulation,PAM)和勒让德多项式分解的简化同步算法。文献[11]在载波同步和定时误差同步环路中引入了卡尔曼滤波替代传统环路中的环路滤波器，提高环路跟踪性能的同时也增加了实现的复杂度。由于以定时误差为参数的似然函数自身的非线性特点，上述文献提出的同步算法均需要差分匹配滤波器来近似计算定时误差，因此引入了近似误差，而且差分运算需要迟和早两路匹配滤波器配合运算，增加了实现的复杂度。

本文利用最大似然估计理论推导了载波相位和定时误差的鉴别器闭合表达式。利用线性相位近似，避免了差分运算在定时误差估计中的使用，在降低同步算法复杂度的同时也保证了算法的同步精度。理论上获得了误差鉴别器的S曲线，分析了误差鉴别器的估计特性。仿真结果表明，本文定时误差的估计精度接近修正的克拉美罗下界。由该算法实现的接收系统误码率也接近理想性能。

1 系统模型

SOQPSK-TG调制信号的表达式为[12]

s(t,α)=exp{jφ(t,α)} 。

(1)

式中：φ(t,α)为调制后的相位，

(2)

式中：符号周期为T；h为调制指数；αi为映射后的符号；q(t)是相位脉冲，

(3)

式中：g(t)为频率脉冲函数，L为脉冲持续的符号长度。对于SOQPSK-TG信号，g(t)的表达式如式(4)所示：

(4)

式中：

(5)

A为归一化的脉冲幅度。根据IRIG-106标准,ρ=0.7，B=1.25，T1=1.5，T2=0.5，h=0.5。φ(t,α)可以重新写为

(6)

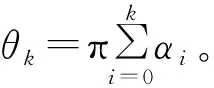
SOQPSK-TG信号经过高斯白噪声信道传输，对于接收端引入了未知载波相位误差φ和定时误差τ。因此，接收信号如式(7)所示：

r(t)=e-jφs(t-τ,α)+v(t) 。

(7)

式中：v(t)表示零均值且功率谱密度为N0的复基带加性高斯白噪声。为了估计出相位误差φ和定时误差τ，采用最大似然理论完成参数误差的估计。那么，N个符号的对数似然函数(Log Likelihood Function,LLF)可以表示为

(8)

为了获得φ和τ的最大似然估计，将LLF的偏导数置为0：

(9)

(10)

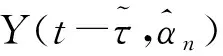
(11)

(12)

式中：

(13)

(14)

一般D取1会获得较好的跟踪性能；BTs为归一化的环路噪声带宽；步进γ=4BTs/kp，kp可由误差鉴别器的S曲线获得[7]。

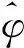
2 基于线性相位近似的误差鉴别器

线性相位近似后的信号相位可以表示为

(15)

式中：

(16)

(17)

n′=n-L′+1。

(18)

式(16)～(18)中：L′≤L是近似后的脉冲长度。为求基于线性相位近似的似然估计，将式(15)代入式(9)和式(10)，可以得到

(19)

(20)

求解式(19)和式(20)，更新后的误差鉴别器可以表示为

(21)

(22)

由式(22)可以看出，求导运算不再出现，eφ(k)不仅用于求解相位误差，同时也用于求解定时误差，整体实现复杂度降低。

因此，以式(21)和式(22)构建的同步算法，结合最大似然序列检测算法(Maximum Likelihood Sequence Detection,MLSD)Viterbi检测器，可以得到整体接收机的结构如图1所示。

图1 接收算法实现框图

S曲线用于分析环路是否存在假锁点。根据文献[13]的定义，S曲线可以表示为

(23)

S曲线的求解要求符号序列α要随机且N要趋近无穷。为了简化S曲线的计算，将α分为28组(SOQPSK-TG中L为8)，只要穷举这些序列即可得到简化后的S曲线表达式为

(24)

对上式求导，可以得到

(25)

L′=1时的S曲线如图2所示，实线为利用式(25)计算的S曲线结果，虚线为通过实际的环路仿真结果。可以发现，两个误差鉴别器均能够保证环路锁定在0误差值上。同时，利用直接判决环路的S曲线具有周期性，在每个整数倍Ts处环路均可以达到锁定，因此环路不存在假锁点。

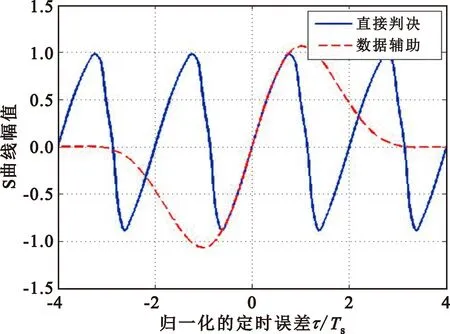
图2 直接判决和数据辅助下的S曲线

3 数据仿真

仿真采用图1的接收机结构，采样频率为1/8Ts，数据为随机产生的二进制序列，映射为SOQPSK-TG的三进制符号α。信道采用加性高斯白噪声(Additive White Gaussian Noise,AWGN)模型，初始定时偏移为0.4Ts，总仿真的符号数为5×105，在5 000个符号后认为环路锁定并开始统计相关数据，环路中跟踪深度D=1。主要仿真了定时误差估计的精度和接收机整体的误码率性能。

3.1 定时误差的估计性能

图3对比了环路噪声带宽BTs分别为10-2和10-3下，本文方法同PAM分解方法在定时误差估计方面的性能。可以看出，当L′=2时本文方法优于PAM分解方法(|K|表示脉冲个数)且接近修正的克拉美罗界(Modified Cramer-Rao Bound,MCRB)[14]，但是实现复杂度和L′=1时相比较高；L′=1时的估计性能和前两种情况相比有所下降，但是其实现复杂度较低，如表1所示。

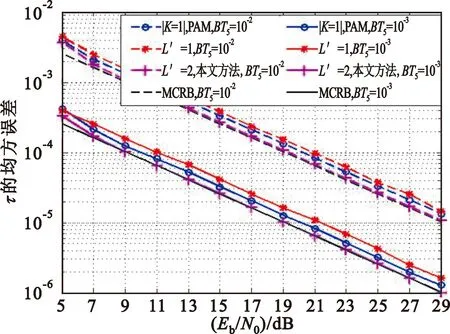
图3 定时误差估计性能对比

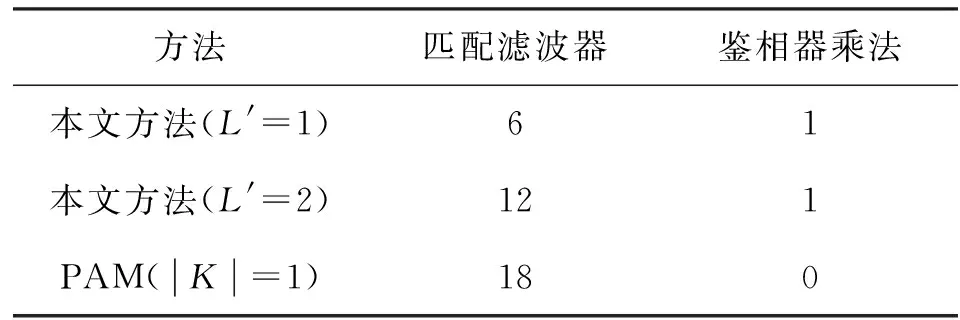
表1 实现复杂度对比

3.2 误码率性能

为了证明本文算法在接收系统中的整体性能，利用图1的接收机结构，测试了本文算法作用在环路带宽BTs=10-3下的误码率，并和SOQPSK-TG的理论性能进行对比[15]，仿真结果如图4所示。

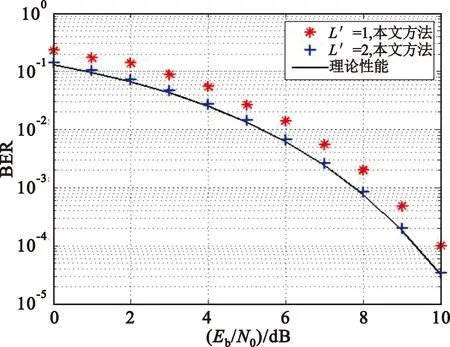
图4 误码率性能仿真

由图4可以看出，L′=2时的误码率性能比L′=1时的优越，主要原因是L′=2对原发射信号的近似优于L′=1，但是从算法实现复杂度上考虑，L′=1的同步算法结构和Viterbi检测器的结构都要更加简单。

4 结束语

本文利用线性相位近似方法，推导了基于最大似然估计的载波相位和定时误差同步环。由于以定时误差信号为参量的似然函数在求导时引入了微分算子，使得同步环结构复杂。线性化相位近似可以避免该微分算子的使用，简化了同步环路的实现结构。仿真结果表明，本文算法在性能和实现复杂度均优于传统的PAM算法。同时，误码率性能测试也证明了本文算法在接收机中的优良性能。但本文只针对静态条件下算法的估计性能进行了研究，对于存在多普勒频移以及动态定时误差时环路的跟踪性能还需后续进一步研究。