基于PPK无验潮的水下地形测量技术研究
2021-04-25魏荣灏陈佳兵
魏荣灏,陈佳兵,徐 达
(1.浙江省水利河口研究院(浙江省海洋规划设计研究院),浙江 杭州310020;2.浙江省河口海岸重点实验室,浙江 杭州 310020)
水下地形测量的主要任务是确定水下起伏形态,主要内容包括测深和定位。测深主要采用声呐进行,定位方式主要有光学定位和无线电定位。最早采用六分仪、经纬仪或全站仪等设备通过天文定位或者光学定位的方法确定平面坐标,采用潮位观测的方式进行验潮。随着无线电定位技术的发展,基于全球卫星导航系统(Global Navigation Satellite System,GNSS)的空基定位技术成为水下测量作业的主要定位手段,而实时动态载波相位差分(Real Time Kinematic,RTK)技术因其可实时提供高精度三维坐标的特点使得无验潮水下地形测量得到了广泛应用。但是,RTK技术需要通过无线电等方式建立实时数据链接以传输载波相位差分数据,在实际测量作业中,由于环境的限制,通讯信号容易发生波动乃至丢失,造成差分数据链接失效,进而导致定位精度严重衰减而无法满足相关作业规范[1]要求,而无需实时数据链接的GNSS载波相位后处理(Post Processing Kinematic,PPK)技术可较好地解决该问题。该技术可望在海洋工程建设、水利工程建设、港口航道建设等方面发挥重要作用。
基于PPK技术获取高精度三维坐标是当前的研究热点之一,国外在此方面的工作较少,而国内已经开展了较多研究:汪连贺[2]联合全球定位系统(Global Positioning System,GPS)的定位信息和惯性测量单元(Inertial Measurement Unit,IMU)姿态信息获取了瞬时水面高程数据,并在烟台港进行了工程试验,结果表明,验潮距离高达98 km时,验潮精度仍优于10 cm;赵建虎等[3]基于GPS事后动态处理技术开展了远距离高精度潮位观测,对垂直基准面转换方法进行了研究,并取得了在100 km范围内的基线距离上,潮位精度优于10 cm的成果;王朝阳等[4]研究了基于PPK和精密单点定位技术(Precise Point Positioning,PPP)的远距离GNSS潮位测量影响因素,研究结果表明,扼流圈天线可提高观测质量,且PPP模式下潮位测量精度优于10 cm;杜锐[5]在远海区域以GPS PPK技术进行了水面高程传递的测试工作,结果表明,该技术定位精度可满足工程需求;王长永等[6]将GPS PPK技术应用于长江口的水深测量工作中,获得了比传统验潮方法更高的作业效率和精度;叶伟等[7]在水库水下地形测量中对PPK技术进行了应用,较好地解决了山区通讯信号遮挡与控制点距离较远导致RTK作业无法进行的问题;刘胜震等[8]在呼伦湖中进行了PPK技术的实际应用,结果表明,该技术在对大面积水域进行水下地形测量时,定位精度可达厘米级。Marcelo Santos等[9]研究了海洋环境中PPK算法的解算策略,提出了一种新的天气延迟模型并改进了解算精度。Jae Young Roh等[10]使用PPK技术处理GNSS浮标观测数据,结果表明,浮标观测水位与验潮站观测水位之差小于±2 cm。
目前,国内相关研究主要基于GPS进行,缺少对不同GNSS系统及其组合解算策略的精度评估。此外,针对入海口等海洋环境的PPK解算精度和稳定性的验证工作也较少,同时国内PPK技术的研究应用领域主要集中于内陆水域,在近海岸特别是杭州湾等强潮河口的应用研究较为少见。为此,本文首先采用不同的GNSS PPK解算策略,对静态比测进行精度和稳定性验证工作,然后使用多GNSS联合解算方法进行了动态比测。比测结果表明,基于不同GNSS系统及其组合的PPK技术的定位精度能满足实际工作需要。最后,在杭州湾涌潮河口的大桥航道监测工作中进行了推广应用,实例结果表明,该技术可为水下地形测量提供技术支撑。
1 PPK无验潮技术原理
PPK无验潮技术主要由两部分组成,第一部分是采用载波相位技术获取高精度的三维坐标成果,第二部分是采用相关的高程转换技术实现潮位控制。
1.1 载波相位差分原理
载波相位差分技术的原理是利用GNSS观测误差在时间和空间上的强相关特性,通过对基准站和流动站的原始载波相位观测数据进行双差计算,消除接收机和卫星时钟的偏差、卫星误差以及大部分的电离层、对流层延迟的影响,达到厘米级的定位精度[11]。
研究者可以从至少两个相隔某一固定距离(称为基线)的GNSS接收机中获得相似的测量值组合,将从两个接收机得到的相似的测量值形成线性组合(差分),就有可能消除两个接收机共有的误差,这样的一个组合称为单差。对来自同一颗卫星的两个单差测量值进行求差,就可以得到双差。利用双差技术处理载波相位观测值,就可以消除大部分的误差源[12]。通过单差消去了卫星星历误差、发射信号的相位和时钟偏差,如果接收机同纬度且相距较近(基线小于50 km),电离层和对流层的大部分误差也消除了。形成双差后,接收机时钟偏差被消去了,仅剩下相位项、整数项和系统相位噪声项。
1.2 PPK无验潮测量原理
PPK技术可通过后处理得到厘米级的测点三维坐标,高程数据一般是CGCS2000(China Geodetic Coordinate System 2000)的大地高数据,处理时需要将大地高转换至目标基准的高程数据,如85高程基准,其原理如图1所示。

图1 PPK无验潮测量原理
水底相对于目标基面的高程可表示为:

式中:H为海底到目标基面距离;H水深为经过天线高改正和吃水改正之后的水深测量值;H大地为该点到大地水准面的距离;ξ为高程异常值。问题的关键在于获取准确的高程异常数据。在小范围的测量中可采用七参数来进行高程转换,大范围则可以使用区域似大地水准面精化进行[13]。
2 精度分析与验证
为了验证PPK在水上作业的稳定性和可靠性,有必要对PPK解算结果的精度、可靠性和稳定性进行分析。但水上作业时测点是在不断运动的过程中获取的,无法像陆地作业时长时间多次重复测量得到多组数据进行平差,因此首先在陆地上选取已知高等级控制点,按照水上作业的数据采集设置进行静态比测,对PPK解算结果的精度、可靠性和稳定性进行评估,然后采用同一GNSS天线,由两台同型号GNSS接收机在船舶上分别进行RTK和PPK观测,假定RTK结果为真值,根据时间戳匹配的方式比较RTK与PPK解算结果的偏差。
本文采用的卫星定位系统包括全球定位系统、格 洛 纳 斯(Global Navigation Satellite System,GLONASS)、北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)、伽利略卫星导 航 系 统(Galileo Satellite Navigation System,Galileo)和准天顶卫星系统(Quasi-Zenith Satellite System,QZSS)。
2.1 静态比测
验证时选取了5个控制点同时进行观测,选取其中一个控制点架设GNSS流动站,其他4个控制点作为基准站,与其距离约为5 km、10 km、15 km和20 km。根据常规作业配置,一般在基准站和远距离移动作业时选用大地型GNSS接收机,其他则使用普通GNSS接收机。因此,在流动站和距离流动站20 km的两个观测点位采用Trimble R9S大地型GNSS接收机,并采用Zephyr Model 2 Geodetic型卫星天线进行观测,其他点位采用Trimble R8S型接收机进行静态比测。所有的GNSS接收机统一观测设置,记录所有可见卫星(GPS、GLONASS、BDS、Galileo和 QZSS) 的多频数据(如GPS记录L1、L2和L5),卫星截止高度角设置为15°,每秒记录一个观测数据。
完成观测后,以Trimble的T02格式下载所有GNSS接收机的原始观测数据并导入Trimble Business Center(TBC)软件进行后处理,后处理时设置卫星截止高度角为15°,采用多频数据处理不同的卫星信号,并分别选用单星、双星和多星组合进行,PPK解算结果与控制点较差统计结果见表1至表7。由于各测站开始和结束的时间略有差异,因此选取同步观测数据进行统计分析,所有的解算模式都得到了3 900个有效解。
由表1至表7可见,在仅使用一个GNSS星座的情况下,GPS解在大部分条件下略优于BDS卫星的解算结果,但两者处于同一量级,所有的平面标准差都处于毫米的量级,垂向的标准差处于厘米量级;比较特殊的是BDS解算结果在20 km处平面标准差最小,且垂向标准差优于15 km解算结果,其主要原因是观测设备不同造成的,在20 km处使用的大地型天线配合大地型GNSS接收机,其性能优于其他测点。使用多个GNSS星座的解算结果明显优于仅使用1个GNSS星座的解,但2个、3个、4个及5个的GNSS星座组合的结果没有显著的差异,平面标准差都小于1 cm,垂向标准差基本都小于1 cm。因此建议在PPK作业时,同时观测所有的GNSS星座,并尽量使用大地型GNSS接收机进行观测。
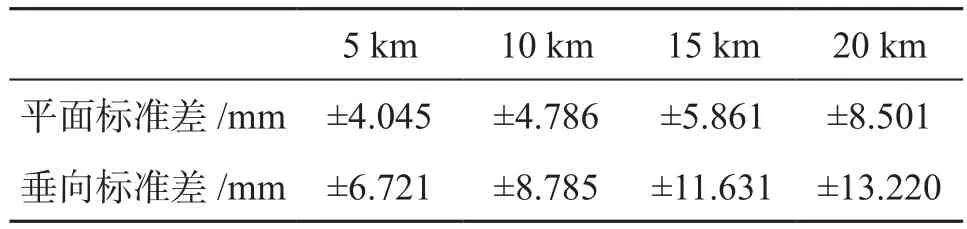
表1 GPS静态比测数据统计表

表2 BDS静态比测数据统计表
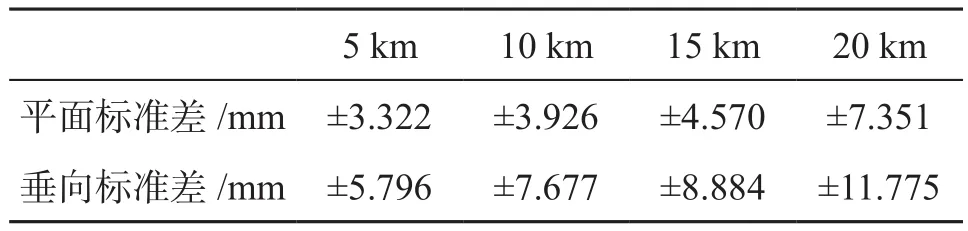
表3 双星静态比测数据统计表(GPS+GLONASS)

表4 双星静态比测数据统计表(GPS +BDS)

表5 多星静态比测数据统计表(GPS+GLONASS+BDS)
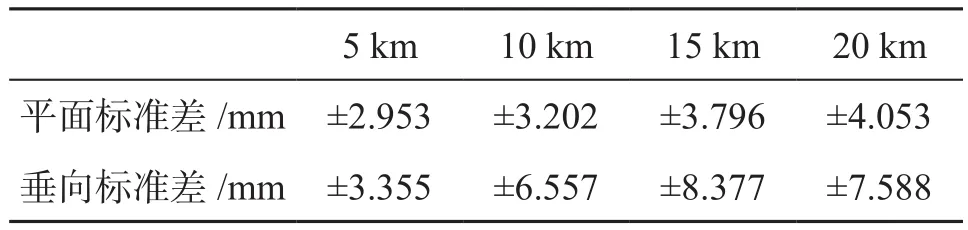
表6 多星静态比测数据统计表(GPS+GLONASS+Galileo+BDS)

表7 多星静态比测数据统计表(GPS+GLONASS+Galileo+BDS+QZSS)
在不同距离观测5个星座得到的PPK解与控制点较差结果如图2所示。从箱型图中可以看出,不同距离的北向、东向和垂向较差都在±5 cm之内,数据分布较为集中,未出现偏差超过5 cm的点。同时,计算得到的平面和三维位置较差基本都小于5 cm。可见在1 Hz观测条件下PPK解算结果较为稳定,具备应用于水上移动作业的能力。

图2 不同距离下多星组合各方向较差(单位:m)
2.2 动态比测
采用船载移动测量的方式对移动测量的精度进行动态比测。在已知控制点上架设GNSS基准站,并在船舶上架设GNSS流动站,在杭州湾河口区域进行测试。所有测站都采用Trimble R9S大地型接收机和Zephyr Model 2 Geodetic型卫星天线进行观测:以10°的卫星截止高度角采集数据,观测5个卫星星座并按1 Hz频率记录原始数据,同时采用基于浙江省连续运行卫星定位综合服务系统(ZJCORS)的网络RTK(使用GPS与GLONASS的双星组合)进行三维定位,使用手簿记录RTK定位结果。野外数据采集结束后,分别下载GNSS基准站和流动站的T02原始观测数据,采用TBC软件进行后处理。
以RTK定位结果为基准,将PPK处理结果通过时间戳匹配后与RTK定位结果求差,其结果如表8所示。从表中可见,各个统计量的中位数与平均值基本一致,数据偏差较小。平面与三维定位结果的标准差都处于厘米量级,同时,各个定位分量较差的平均值都处于厘米的量级,可见RTK与PPK定位结果的一致性较好。
表8中的垂向和三维定位结果较差最大值分别为16.00 cm和17.27 cm,表明仍存在部分数据较差大于10 cm。对数据进行分析,较差超过10 cm的点主要位于测区内桥梁附近,仅使用GPS与GLONASS双星组合基于ZJCORS的网络RTK技术受桥面遮挡,观测卫星数较少导致定位结果不佳。
3 实例应用
测区位于杭州湾口澉浦段附近,该航道河势变化受上游径流和下游潮流的双重影响。由于河床宽浅、潮强流急,涨落潮流路存在较大差异。实测最大涌潮流速约为12 m/s,潮位瞬间最大涨幅2 m以上,实测最大涌潮压力70 kPa。虽然航道所处江道水域最窄仅有约8 km左右,但由于处于涌潮区域且两岸主要为浅滩,基本无法布设验潮站;所处位置的无线电信号一直较差,采用RTK方式作业时数据链接丢失严重,因此采用PPK技术结合单频测深仪进行水下地形测量工作。
数据采集共获取7 072个定位数据,实时获取定位数据(含单点解与浮动解)、PPK定位数据的定位较差如表9所示。从表中可见,野外测量时由于经常发生RTK信号丢失的问题,因此北向、东向实时定位与PPK定位的结果较差的绝对值最大达到了18.569 m和33.430 m,垂向的较差绝对值最大超过了75.932 m,该数据已经完全超出了GNSS系统的单点定位精度,主要由于大桥附近GNSS信号被遮挡及RTK改正信号丢失导致。从平面和三维的定位较差的标准差来看,都已经超过了米级的量级,可见丢失RTK差分信号对定位结果的影响是巨大的。

表8 定位结果比较

表9 实时与PPK定位结果较差表
由于RTK实时信号与PPK信号的定位结果差距较大,因此使用测区附近已有的高程异常模型将RTK与PPK获取的高程数据转换至85国家高程基准后,与同步观测的潮位数据进行验证。图3绘制了作业期间某天的RTK实时潮位、PPK潮位、南北岸和通航孔的潮位站的潮位过程线。从图3上可见RTK实时潮位与PPK解算结果基本是一致的,而丢失RTK差分信号的实时定位潮位数据发生了较大的振荡,已经无法满足RTK三维水深测量的技术要求。PPK潮位与该区域布置的三个潮位站的数据能够较好的吻合,其计算结果可以满足在该区域中进行RTK三维水深测量的精度要求。

图3 RTK实时潮位、PPK潮位与潮位站潮位数据比较图
4 结 论
本文基于载波相位观测原理介绍了载波相位差分技术,通过静态和动态比测的方法进行了精度和稳定性测试后,在杭州湾涌潮河口进行了实际应用,主要结论如下:
(1)静态比测结果表明,20 km距离内现有GNSS系统的PPK解算结果都能符合相关规范要求;动态比测结果表明,RTK和PPK解的一致性较好,平面与三维定位结果的标准差都处于厘米量级。静态比测结果表明,在20 km距离内,现有的GNSS系统都能提供满足相关规范要求的定位结果,多个GNSS系统的联合观测解能提供精度更为稳定的结果;(2)实际应用中PPK解算结果精度可满足RTK三维水深测量的技术要求,能较好地解决RTK差分信号丢失时定位精度严重下降的问题,具有较大的应用潜力;(3)后续有必要在延长测试距离的基础上对更多影响PPK解算结果的因素进行研究,并开展联合RTK和PPK的水下地形测量技术研究。
