水下井口装置与采油树应力计算与分析方法应用

程锐，范海涛，易洁峰，赵宏力，朱麟杰(美钻能源科技(上海)有限公司，上海 200941)

0 引言

在水下井口装置与采油树的设计过程中，存在除了承载紧固件和钢结构外，大量为控压或承压设备，这些设备的零部件存在各种类型的非标设计。为了保证它们在试验和使用过程中的安全性，需要进行大量的力学计算。

在进行初步计算时，需要综合材料、工况等条件，并合理选用许用应力和应力准则[1-2]。在进行有限元分析复验时，还需要对这些工况条件下的应力进行应力分类和线性化，严格按照不同类型的应力进行强度校核[3-4]。本文着重介绍了水下井口装置与采油树所常用的应力计算与分析方法。

1 标准材料与非标准材料

在进行设计计算分析时，我们需要初步知悉所使用材料的机械性能。关于标准材料与非标准材料，其应力计算与分析过程是有所区别的。标准材料是指性能满足或超过表1规定要求的材料；非标准材料是指其性能不满足表1所要求的材料。

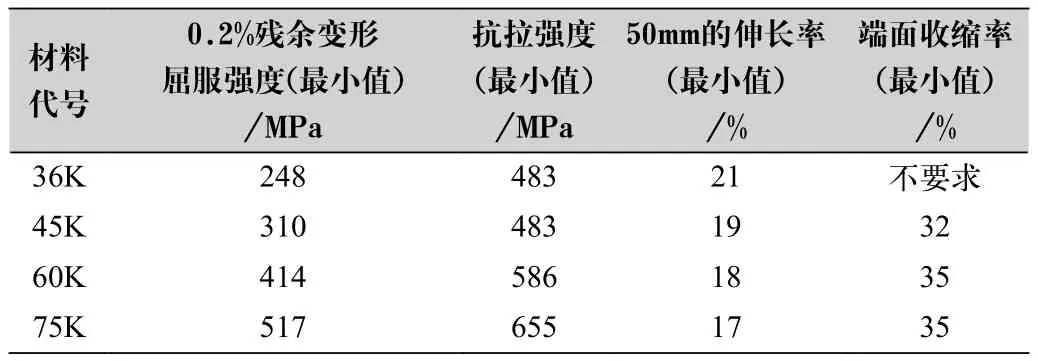
表1 标准材料性能要求

非标准材料最低要求：(1)伸长率不小于15%；(2)端面收缩率不小于20%。

2 许用应力的选择方法

2.1 材料许用应力的选择

2.1.1 标准材料

根据ASME BPVC：2004以及2005和2006增补，第Ⅷ卷第2册附录4所述，对于承压装置的设计计算，设计的许用应力分别按公式(1)和公式(2)中的准则进行限定，ST为静水压试验压力下的最大许用的总体一次薄膜应力强度，Sm为额定压力下的设计应力强度：

式中：Sy为材料规定的最小屈服强度。

2.1.2 非标准材料

根据ASME BPVC：2004以及2005和2006增补，第Ⅷ卷第2册附录4所述，应用于非标准材料承压装置的设计计算，设计的许用应力分别按公式(3)、(4)和(5)中的准则进行限定，ST为静水压试验压力下的最大许用的总体初始薄膜应力强度，Sm为额定压力下的设计应力强度，Ss为初始应力和次应力的最大合成强度：

式中：Rm为材料规定的极限抗拉强度。

2.2 在静水压力试验下当量许用应力

Von Mises 的变形能理论方法可用于承压装置的设计计算。压力容器基本壁厚可在静水压试验压力的基础上，结合三维应力确定其尺寸，并受下列准则限定：

式中：SE为按变形能理论方法计算的在压力容器壁内最高应力处的最大许用当量应力。

2.3 许用剪应力

在纯剪切的拉压二向应力状态下(主应力按大小顺序排列 )：S1=τ，S2=0，S3=-τ，对于塑性材料，按最大切应力理论得强度条件为：

式中：[S]为许用拉应力。

另一方面，剪切的强度条件是：

式中：[τ]为许用剪应力。

比较式 (7)、(8)得：

如果按畸变能密度理论，则纯剪切的强度条件是：

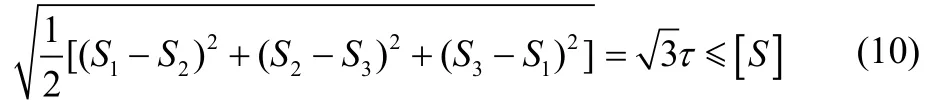
比较式 (8)、(10)得：

按畸变能密度理论，在额定压力下，许用剪切应力：

按畸变能密度理论，在测试压力下，许用剪切应力：

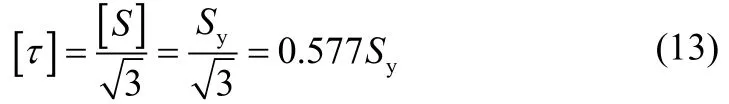
在实际应用过程中，参考ASME BPVC或API 6X标准，一般在额定压力下取 [τ]=0.4Sy；在测试压力下取 [τ]=0.5Sy。

2.4 许用挤压应力

三向应力S1+S2+S3≤4[S]，在额定压力下，许用挤压应力：

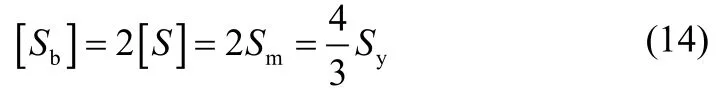
在测试压力下，许用挤压应力：

2.5 封闭螺栓许用应力

封闭(承重载)螺栓的最大许用拉应力SA应考虑螺栓预紧力(对于API Spec 6A应用环境，一般要求50%最小屈服强度的预应力；对于API Spec 17D应用环境，一般要求67%至73%最小屈服强度的预应力)、额定工作压力和静水压试验压力等工况。螺纹小径的栓接应力不超过下述限定：

2.6 主要构件的设计要求

主要结构件(例如：导向基座)应根据认可的工业作法设计，设计计算中使用的基于材料最低屈服强度的安全/设计系数不应小于 1.5。ISO 13628-7 给出了其他载荷条件的设计(安全)系数。

3 应力分类

3.1 应力分类

(1) 一次应力 (Pm，PL，Pb)：指由所加 (机械 )载荷引起，需满足内外力及力矩平衡的正应力或剪应力。该类型应力不自限，它可导致结构失效或总体变形。一次应力包括一次薄膜应力和一次弯曲应力。一次薄膜应力分为总体的和局部的两类，总体一次薄膜应力Pm，截面沿壁厚均匀分布，在结构中的分布不会由于屈服而引起载荷再分布；受结构不连续和载荷转移而引起过量变形的薄膜应力，其可重新分布，它具有二次应力的某些特征，但从保守角度考虑，划分为局部一次薄膜应力PL。一次弯曲应力Pb是指满足内外力及力矩平衡的沿壁厚线性分布的弯曲应力。

(2)二次应力(Q)：由于相邻组件的相互约束或结构的自身约束所引起的法向应力或剪应力。二次应力是自限的。局部屈服和小变量可以使引起这种应力的条件得以满足，一次性施加这种应力是不会导致失效的。总体热应力和总体结构不连续处的弯曲应力属于二次应力。

(3)峰值应力(F)：指由局部结构的不连续或局部热应力的影响而引起的附加于一次加二次应力的应力增量。峰值应力同时具有自限性和局部性，不引起任何显著的变形，之所以有害仅因为它是可能导致疲劳裂纹和脆性断裂的原因。对于并不高度局部性的应力，如果它不引起显著的变形，它也属于这类应力。

3.2 应力线性化许用应力

总体一次薄膜应力的当量应力：

局部一次薄膜应力；

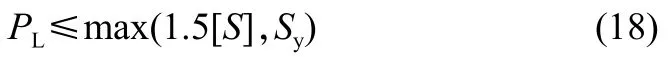
一次应力：

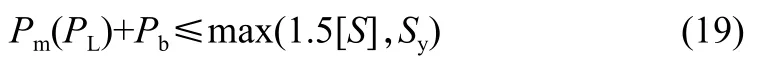
一次应力与二次应力和(确保结构安定性)：

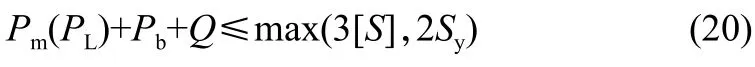
总体应力：

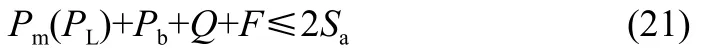
式中：Sa是对操作循环的规定次数由疲劳曲线所得的交变应力。

3.3 极限载荷原理

总体一次薄膜应力Pm与一次弯曲应力Pm的共存关系为：

在试验条件下，由于既要超压以达到考验容器强度，排除可能存在缺陷的目的，又不致使容器超压过大而造成某些地区的屈服甚至引起残余变形，所以规范规定了对试验压力值的限制。其原理是将试验压力所引起的Pm(PL)+Pb、Pm值超过设计状态的许用值，在试验时允许达到外轮廓曲线所包围的极限状态以内；和设计状态相似，规范为应用的方便而做了简化并偏于安全，将内轮廓抛物线用水平直线替代，并把一段抛物线近似用直线表示，所以在斜截面线中的范围即为试验时对Pm(PL)+Pb、Pm的限制范围 (图 1)。

(1)在试验条件下，要求一次薄膜应力Pm≤0.90Sy时，则一次薄膜应力加一次弯曲应力：当Pm≤0.67Sy，则；Pm+Pb≤1.35Sy；0.67Sy≤Pm≤0.90Sy，则Pm+Pb≤2.15Sy-1.2Pm。

(2) 在试验条件下，要求一次薄膜应力Pm≤0.80Sy时，则一次薄膜应力加一次弯曲应力：当Pm≤0.67Sy，则；Pm+Pb≤1.20Sy；当 0.67Sy≤Pm≤0.80Sy，则Pm+Pb≤2.20Sy-1.5Pm。

(3)在额定工作压力下，要求一次薄膜应力Pm≤0.80Sy时，当Pm≤0.67Sy，则；Pm+Pb≤1.2Sy；当 0.67Sy≤Pm≤0.80Sy，则Pm+Pb≤2.004Sy。

(4)在额定工作压力下，要求一次薄膜应力Pm≤0.67Sy时，Pm+Pb≤Sy。

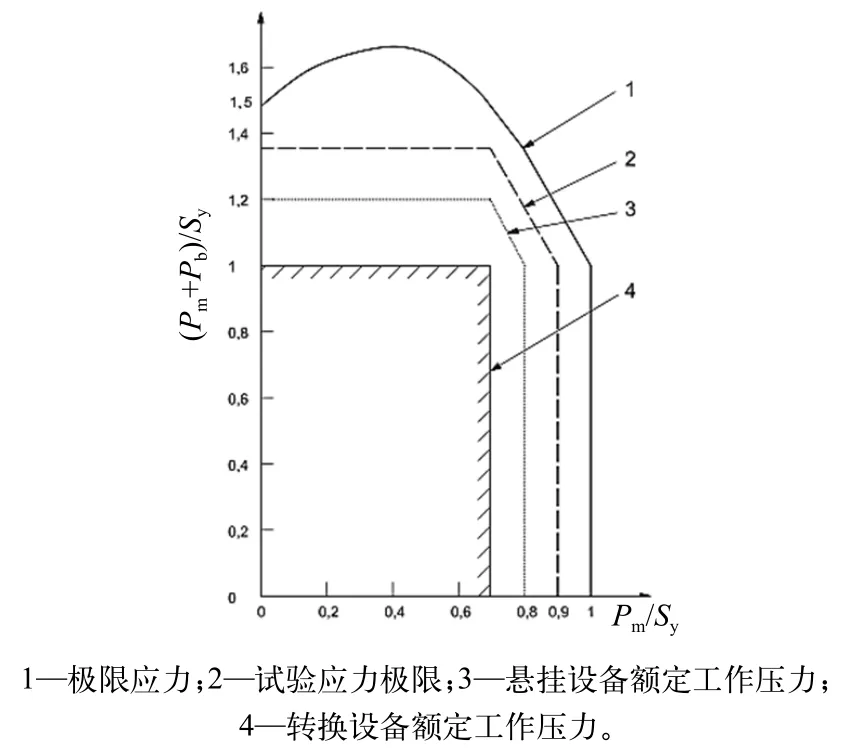
图1 应力极限图

4 应力线性化有限元分析

在基本设计完成后，我们需要进行有限元验证，根据已经确定的工况，选用对应的应力线性化判定准则，完成模型的应力分类和应力线性化评价。本节采用阶梯型压力管道，在仅受内压的条件下针对额定工作压力(69.0 MPa)和测试压力(1.5倍额定工作压力)两种工况进行应力线性化有限元分析，对相关方法进行初步介绍。压力管道选用F2275K标准材料(最小屈服强度517 MPa，泊松比0.30，弹性模量189 GPa)。

4.1 在额定工作压力下

在仅受额定内压的情况下，内部压力载荷与固定约束如图2所示。

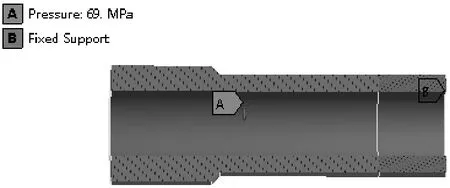
图2 内部压力载荷与固定约束

载荷设定后，进行有限元分析，获得应力云图，在大端、变径(结构不连续)、小端各取两个截面沿壁厚进行应力线性化分析。一次薄膜应力沿壁厚呈平均分布，一次弯曲应力沿壁厚呈线性分布。在壁厚无变化段，在不考虑误差和圣维南定律的局部影响的情况下，一次薄膜应力和弯曲应力在沿截面的轴线上，应力分布具有一致性。但是，在变径段，局部薄膜应力和弯曲应力重新分布。

4.2 在测试压力下

在仅受额定内压的情况下，内部压力载荷与固定约束如图3所示。

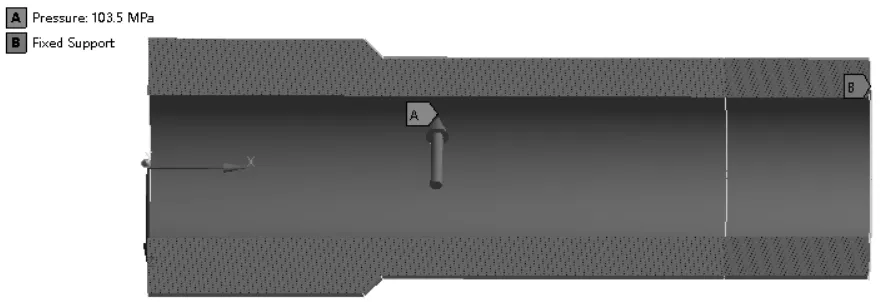
图3 内部压力载荷与固定约束

载荷设定后，进行有限元分析，获得图4所示的应力云图，在大端、变径(结构不连续)、小端各取两个截面沿壁厚进行应力线性化分析。

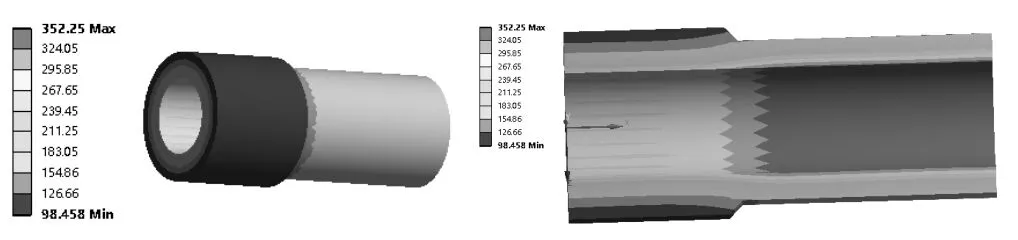
图4 应力云图

一次薄膜应力沿壁厚呈平均分布，一次弯曲应力沿壁厚呈线性分布。在壁厚无变化段，在不考虑误差和圣维南定律的局部影响的情况下，一次薄膜应力和弯曲应力在沿截面的轴线上，应力分布具有一致性。但是，在变径段，局部薄膜应力和弯曲应力重新分布。

5 结语

水下井口装置与采油树是水下生产系统的上游终端设备，它是上游关键的控压和承压设备，这些设备存在大量的非标设计，需要根据遇到的各种材料和工况，选择合适的强度准则和许用应力进行设计计算分析。同时，为了保证计算的准确性和有效性，还需要进行有限元计算分析。在有限元分析过程中，我们需要对各种应力类型进行划分和应力线性化，并按照不同的应力类型和强度判定准则进行结构强度的判定。应力线性化是一个较为复杂但不可或缺的工作，有些条件下(例如：结构不规则、流固热多载荷耦合)，某些类型的载荷并不能直观的判定，需要在设计过程中进行工况简化和复合，并根据经验合理考察。