地球−火星引力辅助下的地−火无动力循环轨道

臧诗慧 武 迪

(清华大学航天航空学院，北京100084)

2020 年是火星探测大年，阿联酋的“希望号”火星探测器、中国的“天问一号”火星探测器以及美国的“毅力号”火星车均成功发射，掀起了火星探测的热潮。火星表面载人科考站是人类走向火星的必由之路，此类科考站需定期更换人员、补充物资，并要求能够往返于地球与火星之间的航天器执行相应的客货运任务。这些航天器需要配备大质量的生命维持系统以及足够大的船员活动空间，因此每次变轨都会消耗大量的燃料。地−火无动力循环轨道是一种往返于地球与火星之间的无动力轨道，运行在这种轨道上，航天器能够消耗较少燃料执行地球与火星之间的客货运任务。由此飞船结构强度的要求能够有所降低，飞船的使用寿命也可相应延长，可以用于执行地球与火星之间定期的货运或者客运任务。

目前，火星短期居住站的设计已经涉及到地−火循环轨道，利用运行在这种轨道上的航天器以及地球与火星各自的接驳航天器，可以实现定期的人员更换与物资补充[1-2]。地火循环轨道器的设计与结构也在近年来被提出[3]。Hollister[4]在 1969 年对地球−金星往返轨道的研究中，首次提出循环轨道的概念，并计算得到地球−金星循环轨道,同时首次提出了地−火循环轨道。

1985 年 Aldrin 提出 “Aldrin 循环轨道”，使用两艘飞船进行地−火与火−地间的运输，但是航天器与地球、火星交会时的速度比较大，实用性受到限制[5]。McConaghy 等[6]在理想的太阳系模型下，忽略火星引力的作用，利用自由返回轨道的组合，得到了若干地−火循环轨道。Ocampo 基于上述结果，总结出地火循环轨道的系统性搜索方法，使用p,h,s,i四个参数确定一条地火循环轨道，其中，p表示一个循环周期包含的地球火星会合周期数，h表示一个循环周期包含的整圈转移轨道或半圈转移轨道数，s表示一个循环周期包含的一般转移轨道数，i表示一个循环周期内飞船绕日的圈数。优化甩摆角的大小以获得一条唯一确定的循环轨道。遍历四个参数，并以有解性、甩摆角比为标准，得到了较为实用的地−火循环轨道集合[7]。一些研究在地火循环轨道中引入推力，Chen 等[8]在地火循环轨道中引入小推力，通过减少航天器与火星交会时的剩余速度以优化循环轨道，Vergaaij 等[9]提出了基于太阳帆动力的地火循环轨道。

2015 年，Rogers 等[10]基于速度杠杆变轨以及小推力过程提出了航天器进入循环轨道的优化方案。2016 年，Anderson[11]研究了在与地球交会时，接驳航天器与循环轨道器交会的轨迹规划与燃料消耗问题，进一步完善了地火循环轨道的应用研究。

然而，这些模型均忽略了火星引力的影响，默认航天器在火星引力影响球外飞掠。同时部分轨道的效率较低，航天器每运行十几年才能够完成一次地球−火星之间的往返。本文将在此基础上引入地球与火星的引力辅助。多圈转移轨道会显著地增加地−火转移的时间，拉低轨道器的效率，故本文放弃使用整圈转移轨道，仅使用半圈转移轨道，寻找更加高效的地−火无动力循环轨道。

1 地−火无动力循环轨道的动力学模型

1.1 动力学模型

本文采用理想化的太阳系动力学模型进行计算，仅考虑太阳的中心引力作用，地球和火星位于共面圆轨道上。在实际轨道设计中，可以将本文模型的计算结果作为初值，采用摄动法求解高精度模型下的无动力循环轨道。因此，本文采用的坐标系和动力学模型定义如下：

(1)太阳位于惯性坐标系原点，仅考虑太阳的中心引力作用，地球与火星位于共面圆轨道上；

(2) 地球轨道半径为1 AU，周期为1 a，火星轨道周期为1.875 a;

(3)地球的引力常数µe=3.985 00×105km3/s2，火星的引力常数µm=4.281 73×104km3/s2。

根据文献[6]，火星的轨道周期设为1.875 a。在此情况下，地球与火星的相对几何关系具有周期性，周期为 15 a。因此，在本文中，地火转移的窗口搜索设置为转移初始时地球与末端时火星间的相角差，每隔15 a 均会有一次相同的发射窗口。实际应用中，应将此相角差转换为真实的发射时刻。

1.2 地火间的 Lambert 转移

进行地火转移时，探测器需要在特定的时间Te−m内从地球轨道上的特定位置re转移到火星轨道上的特定位置rm，这个问题可以用Lambert 转移的解法求解。本文使用Lambert 问题已有的求解程序[12]，仅考虑飞行器转移轨道公转小于一周期的情况。初末位置矢量与转移时间确定，则Lambert 转移轨道唯一确定。

以图1 为例，航天器从re转移到rm，转移时间为Te−m，可以使用求解程序得到航天器的初始速度矢量、末端速度矢量，从而得到相应的Lambert 转移轨道(黑色曲线)。由于地球和火星的轨道为共面圆轨道，因此初始的地火Lambert 转移轨道由转移时间Te−m和相角差完全确定。此外，火地Lambert转移可以进行类似求解，转移时间记为Tm−e。

图 1 地火 Lambert 转移

1.3 半圈转移轨道

本文以地火半圈转移轨道作为辅助轨道，从而实现地−火无动力循环轨道的设计与搜索。传统的自由返回轨道需要在地火Lambert 转移后，经过火星引力辅助进入Lambert 转移返回，但此种轨道存在剩余速度过大、发射窗口较少的问题。因此，本文引入了半圈转移轨道作为辅助轨道，即在进行引力辅助时可以选择进入和中心天体周期相同、具有半周期自由返回特性的圆轨道，以选择合适的返回时机降低剩余速度，实现地−火无动力循环。

设在引力辅助过程中，航天器仅受行星引力的影响。航天器在飞掠行星前的速度可以分解为行星公转速度Vp与航天器相对行星的剩余速度V∞的矢量和。由于航天器飞掠时间较短，飞掠前后Vp近似不变，V∞大小不变，方向改变。调整航天器近星点的赤经赤纬以及高度，可以控制飞掠后V∞的指向。如图2，由于飞掠后V∞大小不变，方向可以改变，所以飞掠后航天器的速度分布在一个以Vp终点为球心，V∞大小为半径的球面A上。

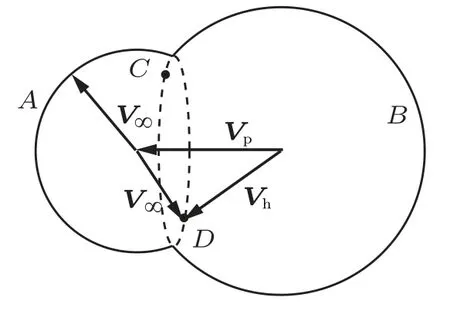
图2 引力辅助中的速度叠加

球面A与以Vp起点为球心、以Vp大小为半径的球面B相交，形成交线圆，分布在交线圆上的速度矢量大小与Vp相等。如果引力辅助后的航天器的速度矢量分布在这个交线圆上，同时航天器的日心距与行星的日心距相同，根据以下轨道能量的公式，航天器半长轴与行星半径相同，周期与行星的周期相同。

式中a为轨道的半长轴，µp为中心天体的引力常数，v为航天器的速度大小，r为航天器与中心天体的距离。

由于航天器位置矢量垂直于Vp，过Vp并垂直于位置矢量的平面一定与交线圆有两个交点，即交线圆上一定存在两点C、D与位置矢量垂直。则引力辅助后的航天器将进入与行星轨道半径相同的圆轨道，这个轨道与行星的圆轨道有一定的夹角，其夹角γ可以根据剩余速度求得。

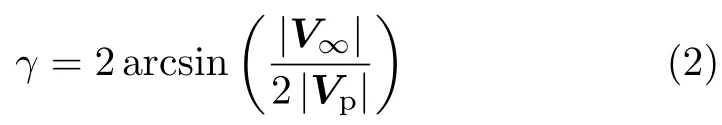
运行在这个轨道上的航天器半年后会再次回到行星公转的平面，与原行星交会。假如微调轨道，使得航天器在再次交会时与原天体保持一定的距离，不受其引力影响，则航天器可以每半年与行星交会一次。这个轨道被称为半圈转移轨道，如图3。

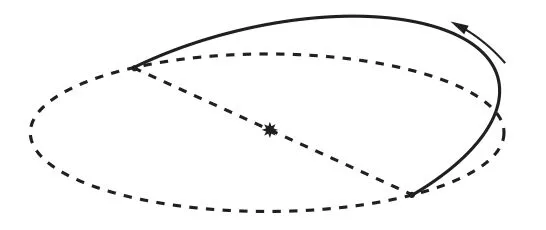
图3 半圈转移轨道

2 地−火无动力循环轨道的设计

文献[2-7]将循环轨道定义为一个周期后天体和航天器相对几何位置复原的轨道，其中相对几何关系包括航天器相对地球的位置以及火星相对地球的位置。如果在这个定义下同时考虑地球与火星的引力辅助作用，则轨道既要满足时间约束，又要满足地−火、火−地转移Lambert 转移的约束，导致问题约束较多，无法寻找到具有使用价值的循环轨道。

事实上，相对几何关系复原并不是地−火循环轨道功能的本质要求，只要航天器在这个轨道上能不断无动力往返于地球与火星之间，那么这条轨道就具有同样的功能。本文考虑放宽地火无动力循环轨道的定义，不再要求这个轨道具有周期性，能够不断无动力往返于地球与火星之间即可。

2.1 约束条件

2.1.1 甩摆角(引力辅助高度约束)

图 4 中δ为航天器进行引力辅助时的甩摆角。计算公式为

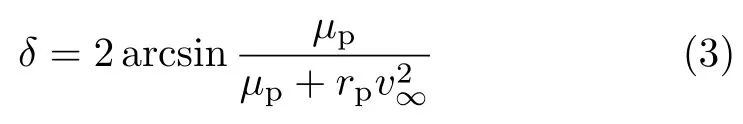
式中，µp为中心天体的引力常数，rp为双曲线轨道近星点半径(也称甩摆半径)[13]。

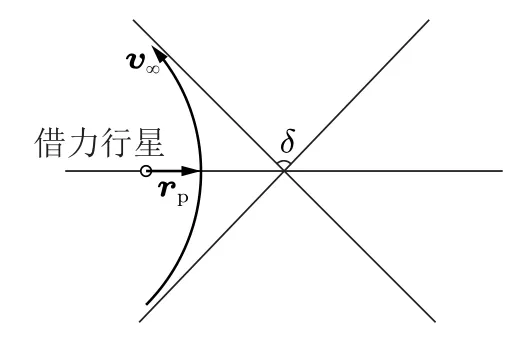
图4 引力辅助中的甩摆角

当剩余速度固定时，甩摆角越大，则近星点高度rp越小。由于现实中的地球与火星并不是一个质点，航天器在飞掠的时候近星点必须在大气层外，因此甩摆角不能太大。本文要求航天器近星点高度的最小值为200 km。相应的甩摆角为最大甩摆角δmax。

定义甩摆角比Tr=δmax/δ，其中δ为实际甩摆角。如果Tr>1，则引力辅助可行，如果Tr<1，则引力辅助不可行。

2.1.2 剩余速度约束

剩余速度决定了航天器在天体引力场内的轨道能量，从天体表面或者近地轨道出发的航天器要与循环轨道器进行对接，需要加速使轨道能量近似相等，航天器之间才有可能进行对接。循环轨道器的剩余速度越高，则接驳航天器要有更强的变轨能力，如此将会消耗更多的能量。本文考虑将循环轨道器在地球与火星引力场内的剩余速度大小v∞e与v∞m限制在 10 km/s 以内，如果进行一次地−火或火−地转移后的剩余速度大于10 km/s，则判定此次转移不符合限制条件，航天器进入半圈转移轨道等待下一次转移，直到转移之后的剩余速度小于10 km/s。

2.2 计算步骤

地−火往返过程可以分为以下5 个步骤：

(1) 从地球转移到火星，初始转移角度为θ0，转移时间为t0；

(2)在火星轨道上进行半圈循环，等待合适的时机进行火−地转移；

(3) 从火星转移到地球；

(4)在地球轨道上进行半圈循环，等待合适的时机进行地−火转移；

(5) 进行下一步地−火转移。

2.2.1 从地球转移到火星

设航天器第一步地−火转移在地球与火星公转平面内进行，转移具有两个自由度，因此定义初始转移角度θ0与初始转移时间t0为确定第一步地−火转移的两个自由变量。同时定义两个参数θe(t)与θm(t)，作为描述地球与火星位置的参数，不妨定义θe(0)=0，其中t为航天器在轨道上的运行时间，单位为a。地球与火星在时刻t时的坐标为

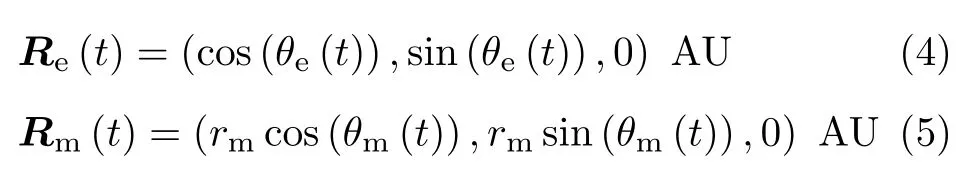
式中，rm为火星公转半径，单位为AU。地球与火星的公转速度矢量为

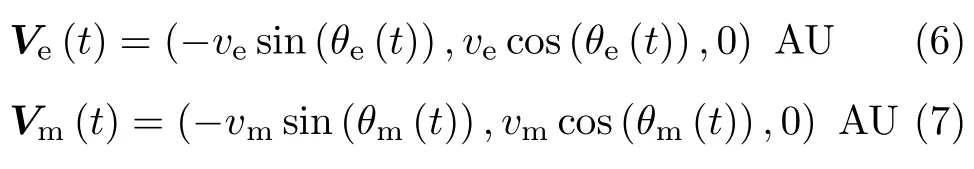
式中，ve和vm分别为地球与火星公转的线速度大小。见图5，可得航天器第一次转移的终态位置R−为

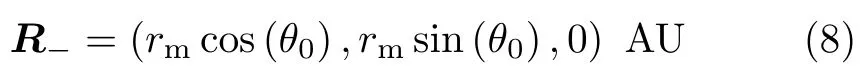
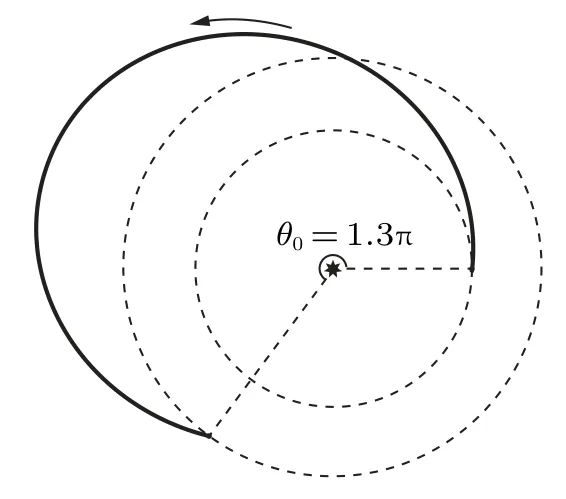
图 5 第一次地−火转移 (θ0 =1.3π，t0 =1.62 a)

当t= 0 时地球的坐标R+= (1,0,0) AU，则第一步地−火转移的Lambert 方程确定，有唯一解，可以由式(9) 解出转移前后的航天器速度。

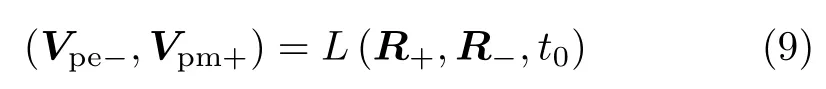
式中，L为Lambert 转移的求解函数。

同时可得第一次地−火转移开始时，火星与地球的相位差θm(0)

计算得到航天器在地球引力场内剩余速度大小v∞e和航天器在火星引力场内剩余速度大小v∞m

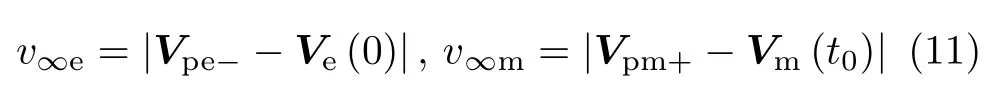
2.2.2 在火星轨道上进行半圈循环

首先计算火−地转移，以航天器转移前后位置矢量之间的夹角θa为未知数，θa∈(0,2π)，则第二次转移的初始位置矢量R+为

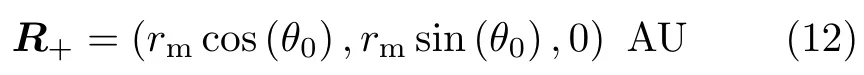
终态位置矢量R−为

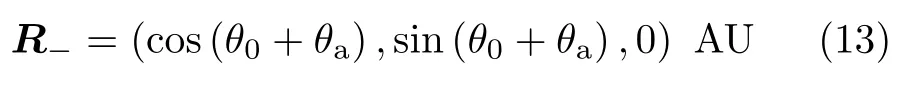
转移时间ta为

相应的Lambert 转移有唯一解

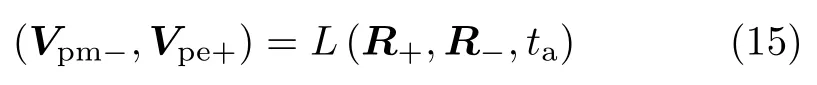
以θ0=1.3π，t0=1.62 a 时为例，画出关于θa的函数图像，见图6。由于航天器在火星引力场内进行的是无动力的引力辅助，因此引力辅助前后航天器的剩余速度不变，要求由图可知，这个方程存在两个解，为尽可能减少航天器转移的时间，本文均取转移时间较短的解。使用拟牛顿迭代法可以在10 步左右得到θa较为精确的数值解。计算得到火 − 地转移的甩摆角δ=⟨Vpm+Vpm−⟩以及地球引力场内的剩余速度v∞e=|Vpe+−Ve(t0+ta)|。如果δ > δmax即Tr< Trmin或者v∞>10 km/s，则判定此次转移不可行，进入火星半圈转移轨道等待下一次窗口(图7)。如果转移可行，则直接进入第三步。

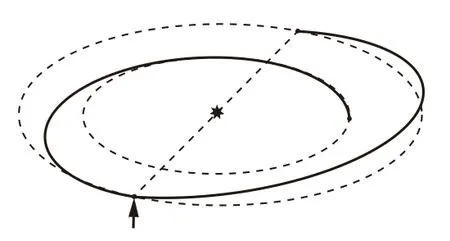
图 7 进入半圈转移轨道 (θ0 =1.3π，t0 =0.8 a)

探测器进入半圈转移轨道的速度为

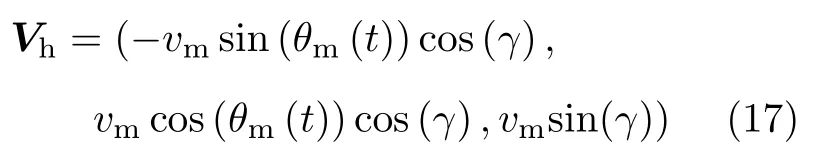
Tr=⟨Vm+Vh⟩，如果Tr<1，则此次循环轨道终止，无法进行下一步转移，退出计算。若Tr>1，则航天器进入半圈转移轨道。

2.2.3 进行火−地转移

航天器运行半个周期后，重复火−地转移的计算，如果可行，则进行火−地转移(图8)。如果不可行，则继续重复第二步的半圈循环，定义Nm为航天器在火星半圈转移轨道上等待的次数。

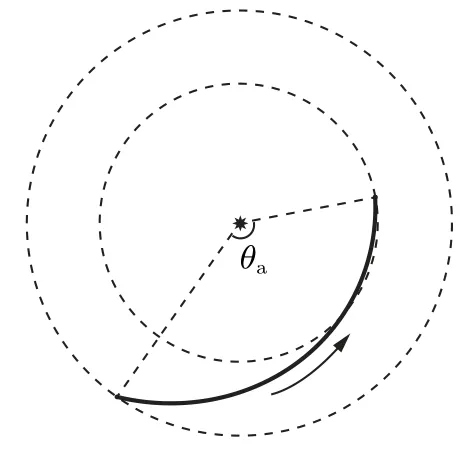
图 8 火地转移 (θ0 =1.3π，t0 =1.62 a)

为保证航天器等待的时间不过长，限制航天器每次在半圈转移轨道上的等待次数N不超过10 次。

第四步的计算过程与第二步类似，航天器在地球半圈转移轨道上循环，直到存在合适的窗口，定义Ne为航天器在地球半圈转移轨道上的等待次数。之后进行第五步的计算，与第三步计算过程类似，进行下一步地−火转移。

完成五步计算之后，从第二步开始进行相同步骤的循环，计算下一个地−火循环，直到参数满足算法中的退出条件，停止计算。

图9 为计算的流程图。

3 地−火无动力循环轨道计算结果

3.1 初始参数对范围

并非所有初始参数对(θ0,t0)都能满足初始的限制要求。令初始地−火转移中地球与火星引力场内航天器的剩余速度小于10 km/s，可以得到图10。图中实线区域内的初始参数对满足v∞m<10 km/s，虚线区域内的初始参数满足v∞e<10 km/s，取交集，得到图 11。使用图 11 区域中的初始参数对 (θ0,t0)进行遍历，寻找域内的地−火无动力循环轨道。

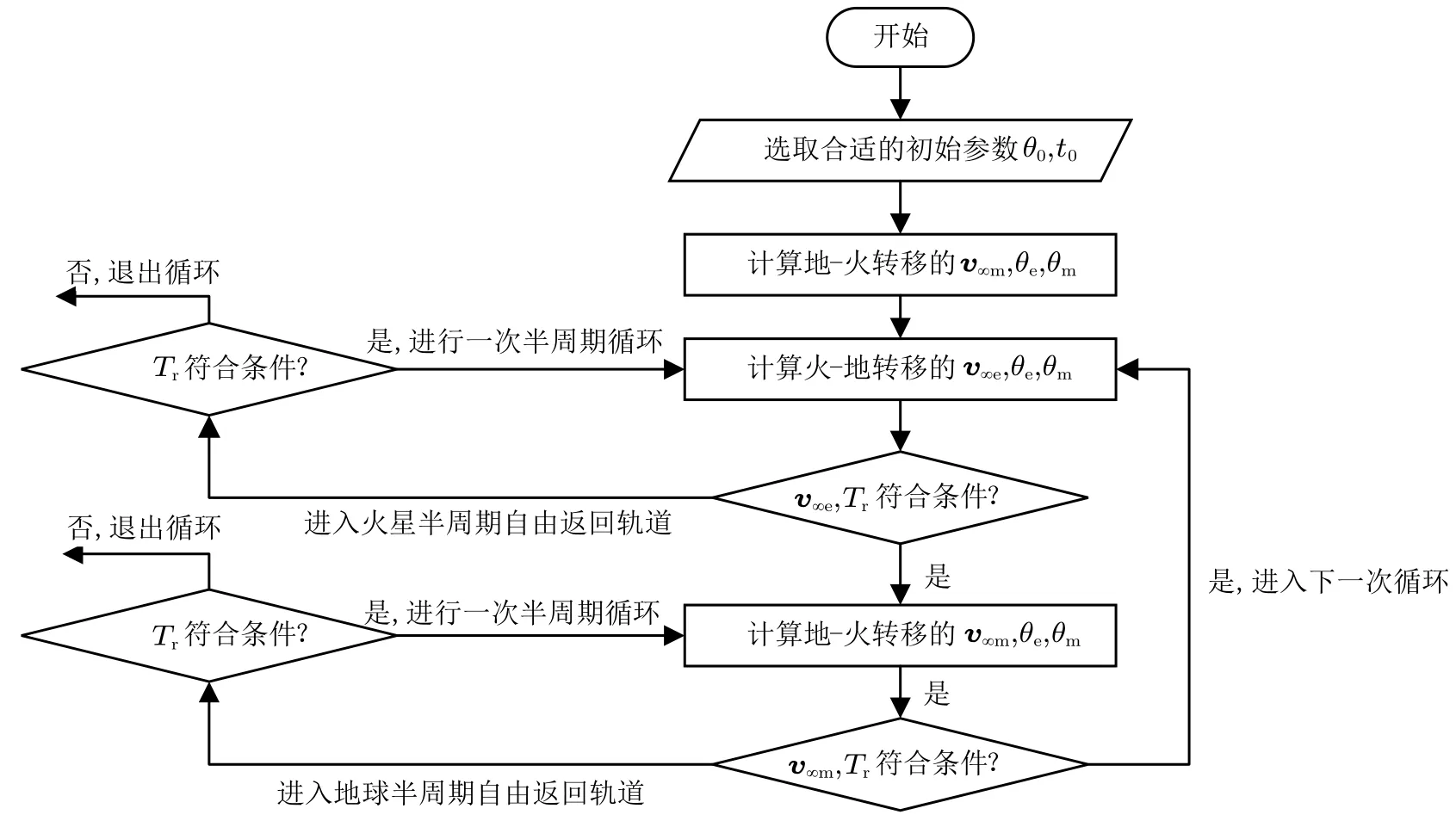
图9 计算流程图

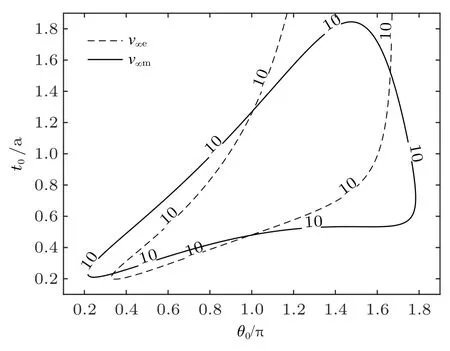
图10 使得剩余速度满足条件的区域

图11 初始参数对范围

3.2 n 次地−火无动力循环轨道

根据流程图所示 (图 9) 进行计算 (使用 CPU AMD Ryzen 5 4600H，主频 3.0 GHz，内存 8.00 GB配置的笔记本电脑，Matlab 程序运行耗时约 7 h)，得到一系列地−火无动力循环轨道。挑选其中循环次数较多的几个轨道，参数与相关数据列于表1。

以θ0= 1.357π，t0= 0.832 a 为例说明，此轨道为计算结果中除Aldrin 循环轨道外，循环次数最多的轨道(图12)。计算第一步，可得航天器初始时刻从地球离开时速度矢量为(−6.20,31.77,0)km/s，到达火星时速度矢量为(19.10,−8.50,0)km/s，地球引力场内剩余速度大小为6.48 km/s，火星引力场内的剩余速度大小为3.39 km/s，转移前θe=0，θm=1.48，转移后θe=5.23，θm=4.26。

计算第二步，首先判断直接火−地转移的可能性，计算发现不存在能够在一个轨道周期内进行火−地Lambert 转移的轨道，于是转入火星半圈转移轨道，等待合适的窗口。根据式(2)，半循环轨道与火星运行平面的夹角γ= 0.1。循环结束后再次尝试计算火−地转移。最终在循环六次 (三个火星年) 后发现合适的窗口。此时θe= 2.87,θm= 4.26，探测器在火星引力场内剩余速度大小未变，仍然是3.39 km/s。

进入第三步，计算火−地转移的参数，直接代入相应函数，得到航天器在离开火星时的速度矢量为 (18.49,−9.90, 0) km/s，到达地球时速度矢量为 (−20.55,−25.07, 0) km/s，火星引力场内剩余速度大小为3.39 km/s，地球引力场内剩余速度大小为6.29 km/s，转移结束时θe= 0.25，θm= 6.22，转移时间为212 d。

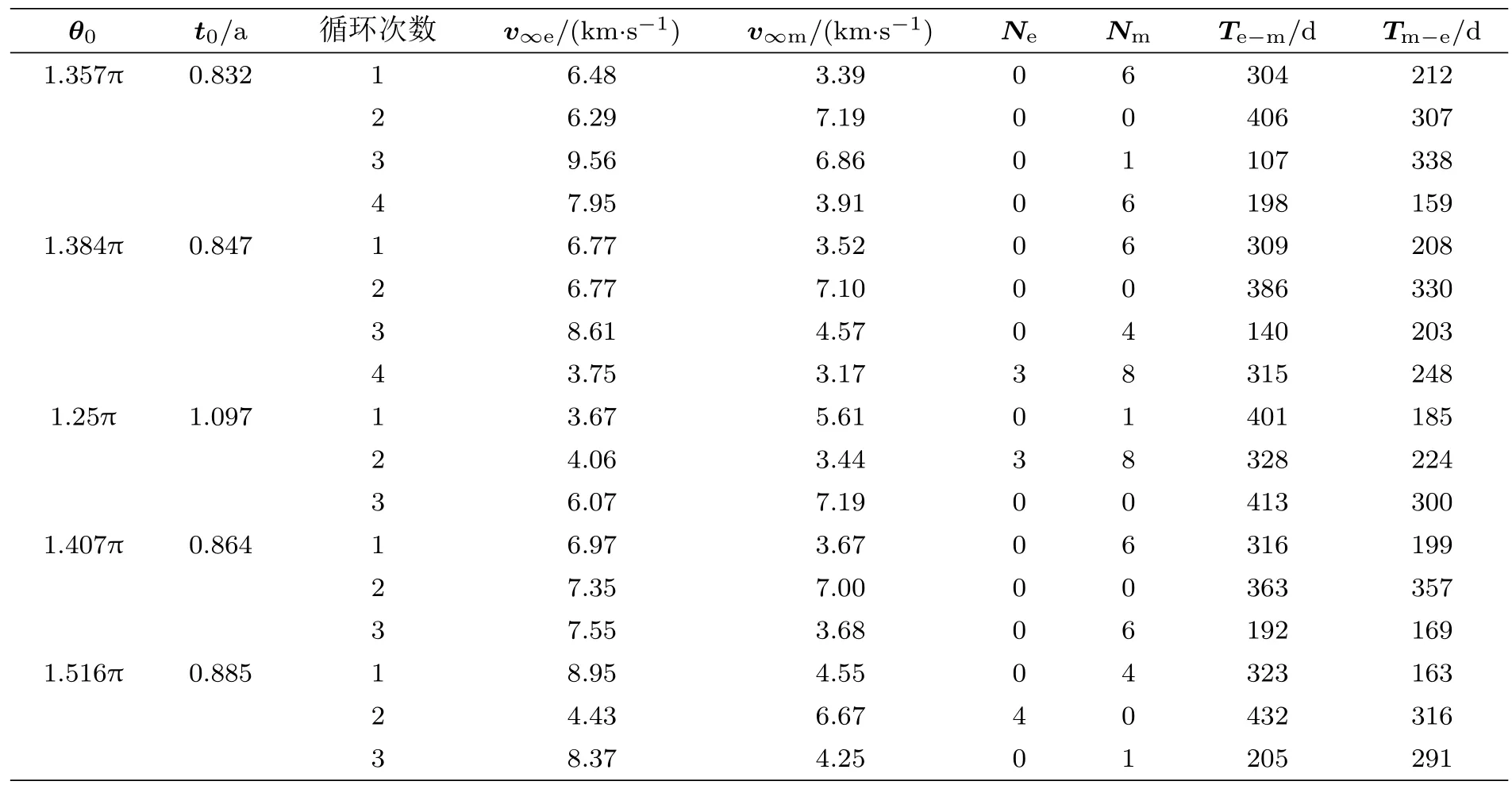
表1 地−火无动力循环轨道计算

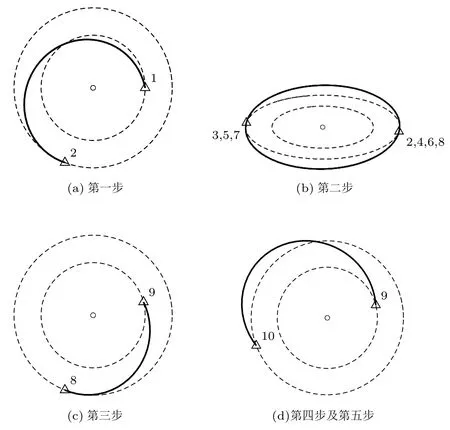
图12 地−火无动力循环轨道算例

进入第四步，首先判断直接地−火转移的可能性，计算发现可以直接转移，跳过第四步进入第五步。代入相应的Lambert 转移函数，得到航天器在离开地球时速度矢量为(−3.13,33.57,0)km/s，到达火星时速度矢量为(12.36,−19.3,0)km/s，地球引力场内剩余速度为6.29 km/s，火星引力场内剩余速度为 7.19 km/s，转移结束时θe=0.95，θm=3.66，转移时间为406 d。

第五步结束后，重新开始第二步计算，进行下一次循环，直到计算无法进行时，退出程序。

最终该轨道能够使航天器在地球与火星之间无动力往返四次，转移最长时间406 d，最短时间107 d。四次往返中，有两次火−地转移需要航天器在火星轨道上待机六个半圈转移轨道，即三个火星年，期间航天器可以在轨道上闲置，待最后一次火星半圈转移轨道结束后，再将人员物资转移到航天器上，进行下一次火−地转移。整个轨道耗时17.76 a，平均每次循环耗时4.44 a，其中第二、第三次循环各自仅耗时 1.95 a，2.16 a。

根据文献[7]，循环轨道周期一般以地火会合周期(约2.14 a) 为单位，通常有两个及以上的会合周期，一个轨道周期中，航天器只完成一次地−火轨道相同，优于三个及以上会合周期的循环轨道，并且本文提出的地−火循环轨道中的部分循环能够在短时间内进行，进行地球与火星间的快速转移。

在高精度模型中，本文所提到的地−火转移轨道具有稳定性。举例而言，上文中初始参数θ0=1.357π，t0= 0.832 a 的轨道在高精度轨道中漂移至θ0=1.352π，t0=0.822 a，误差较小。

航天器完成该轨道时，可以通过变轨进入新的循环轨道或停泊进入地球环绕轨道，执行下一个任务。

4 总结

本文在前人基础上，考虑地球与火星引力辅助效应，引入半圈转移轨道，在剩余速度与引力辅助近星点半径的限制下，给出一种新的地−火无动力循环轨道算法。利用初始转移角度与初始转移时间这两个自由参数进行遍历计算。算例表明，存在能够在18 年间于地球与火星之间无动力往返4 次的循环轨道，效率较高。这些轨道能够作为未来地球与火星之间客运、货运的备选轨道，从而减少航天器燃料消耗，降低运输成本。