锚索受力性能对深基坑安全性的影响
2021-04-25刘先文韩建刚
刘先文,韩建刚
(海南大学 土木建筑工程学院,海南 海口570228)
随着城市化的发展,在限制区域内对空间的需求逐渐扩大,进而对地下空间的发展就越显急迫.但由于当前对地下岩土工程的研究还不够透彻,基坑工程的发展亦处于半理论半经验的阶段,因而使得深基坑桩锚支护结构的设计面临着挑战.所以,在此发展现状下,时有基坑倒塌事故的发生[1],鉴此,有必要对深基坑桩锚支护结构的受力性能作进一步的研究与分析.
关于深基坑桩锚支护体系的受力性能,张钦喜等人[2]的研究表明,锚索的拉力变大会使桩身剪力变小和弯矩变大,对此数值模拟能较好地反映其规律和特点;任君等人[3]的研究也表明,桩锚支护结构具有其土压力小于经典土压力的特点,所以有较大的优化空间.考虑到深基坑桩锚支护结构的内力计算很复杂[4],因此本文采用PLAXIS数值分析软件来模拟基坑开挖的实际情况,以此反映基坑土压力和桩结构的内力情况.此外,蓝文兵[5]的研究表明,水位变化对锚索受力的影响较大,但有关水位变化和桩锚受力对支护体系安全性影响的研究却较少.因此, 本文利用数值模拟软件PLAXIS对广西南宁某深基坑倒塌案例进行了模拟,并对该深基坑的中部锚索施加了不同大小的预应力,研究了锚索受力性能和土压力的分布规律;同时,考虑到了地下水位的因素,分析了桩锚支护结构受力性能对深基坑安全性能的影响,为今后深基坑的锚索设计和施工提出了具有一定参考价值的结论和建议.
1 工程概况和地质情况
该项目位于广西省南宁市,基坑支护深度22.0 m,采用放坡与桩锚支护联合模式,如图1所示.其中,第一级放坡深度为2.0 m,冠梁顶面位于距坑顶2.0 m的位置,桩锚支护结构设有四排预应力锚索,锚索水平间距为1.6 m,竖向间距为5.0 m,第一排锚索距离坑顶2.4 m,桩长26.0 m,锚固长度6.0 m,桩径1.0 m,桩间距1.6 m.锚索的设计参数见表1,M1~M4分别代表第一排到第四排的锚索(以下用M1~M4表示),M1和M2为三股1×7直径为15.2 mm的预应力钢绞线,M3和M4为四股1×7直径为15.2 mm的预应力钢绞线(见表1).


表1 锚索设计参数表
该案例的土层主要由5.0 m填土、6.2 m强风化泥岩、8.5 m强风化泥质粉砂岩以及中风化泥岩组成.根据参考文献[6],土层的具体参数信息见表2.该深基坑已发生长约60 m宽约15 m的塌方事故,并造成了一定的社会影响.

表2 土体物理力学参数
2 锚索支点反力的计算
通过分析和总结大量支撑力和土压力的工程实测数据,Terzaghi和Peck提出了主动土压力的计算简图,如图2所示[7-8],在实际计算中:
(1)当γavHe/cav>4时,用图2(a)的土压力分布模式来进行计算,其中,Ka在[1-4cav/(γavHe)]和0.3中取最大值;
(2)当γavHe/cav≤4时,用图2(b)的土压力分布模式来进行计算.
其中,γav和cav分别为各层土按厚度加权的重度平均值和黏聚力平均值,替代原图式中的γ和c;H为基坑深度,He为支护桩计算高度.
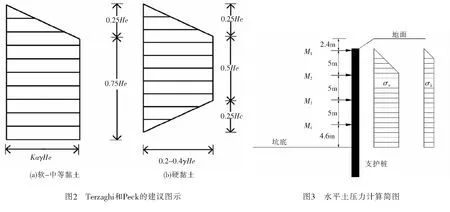
由表2计算得到,γav、cav和He的取值分别为20.355 kN/m3、69.809 kPa和20 m.本案例γavHe/cav5.832>4的,所以用图2(a)来计算其土压力,其中0.25He为5 m,水平土压力σa为:
2.5 果园生草 提倡果园行间生草,通常以自然生草为主。每年4月初在果树行间撒施尿素20 kg/亩,结合浇水,既增加了草的产量,又避免了草与树争肥。当草长到40 cm左右时及时收割,每年生长季节用割草机割草3~4次,秋后用旋耕机全园深翻。自然生草连续进行3年,可以提高土壤有机质1%以上。
(1)桩顶h=2 m时,取σa=0;
(2)h=7~22 m时,取σa=γavHeKa;
其中:Ka=[1-4cav/(γavHe)]=0.314>0.3,取0.314.
(3)h=2~7 m时,σa在(1)、(2)所得的值中按线性插入,如图3所示.
另外,案例中的2 m放坡部分按现行的国家行业规范《建筑基坑支护技术规程》JGJ120—2012第3.4.8条所给公式计算,其附加竖向应力σk,如图3所示.
结合支撑荷载的1/2分担法估算,根据图2计算得到的σa以及图3计算得到的σk进行整理后,得到各锚索作用位置的支点反力FR,如表3所示.

表3 支点反力计算表
在表3得到的数据中,M2所承受的支点反力比M1所承受的支点反力要大,而在该案例中,M2的设计荷载要比M1的设计荷载小29.3%左右;同样,李连祥等人[9]的研究表明,对于较浅的基坑,其支护结构全长范围内的土压力增大,而对于深基坑,其浅层中层部位的土压力增大,这也说明了该案例中对于M2的设计荷载偏小了.
3 数值模型分析
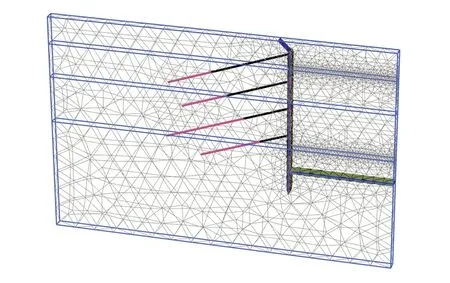
图4 数值模型及网格划分
3.2 模型分析步骤具体计算步骤见表4,在激活每一排锚索的同时施加一定的预应力,为了模拟实际基坑的受力性能,模型分析的控制值为锚索轴力的设计荷载.模型计算的锚索轴力如表5所示,该阶段为地下水位(8 m),且为M1到M4分别施加300 kN、200 kN、500 kN、500 kN预应力时的结果.通过表5可知,所模拟的锚索轴力与设计荷载基本相近,此模型可以反映该基坑实际的受力性能.在此模型的基础上控制水位变化和所施加的M2预应力大小(M1、M3、M4的预应力大小均保持不变)等参数,以此来分析支护结构桩的顶位移和锚索的受力分布.
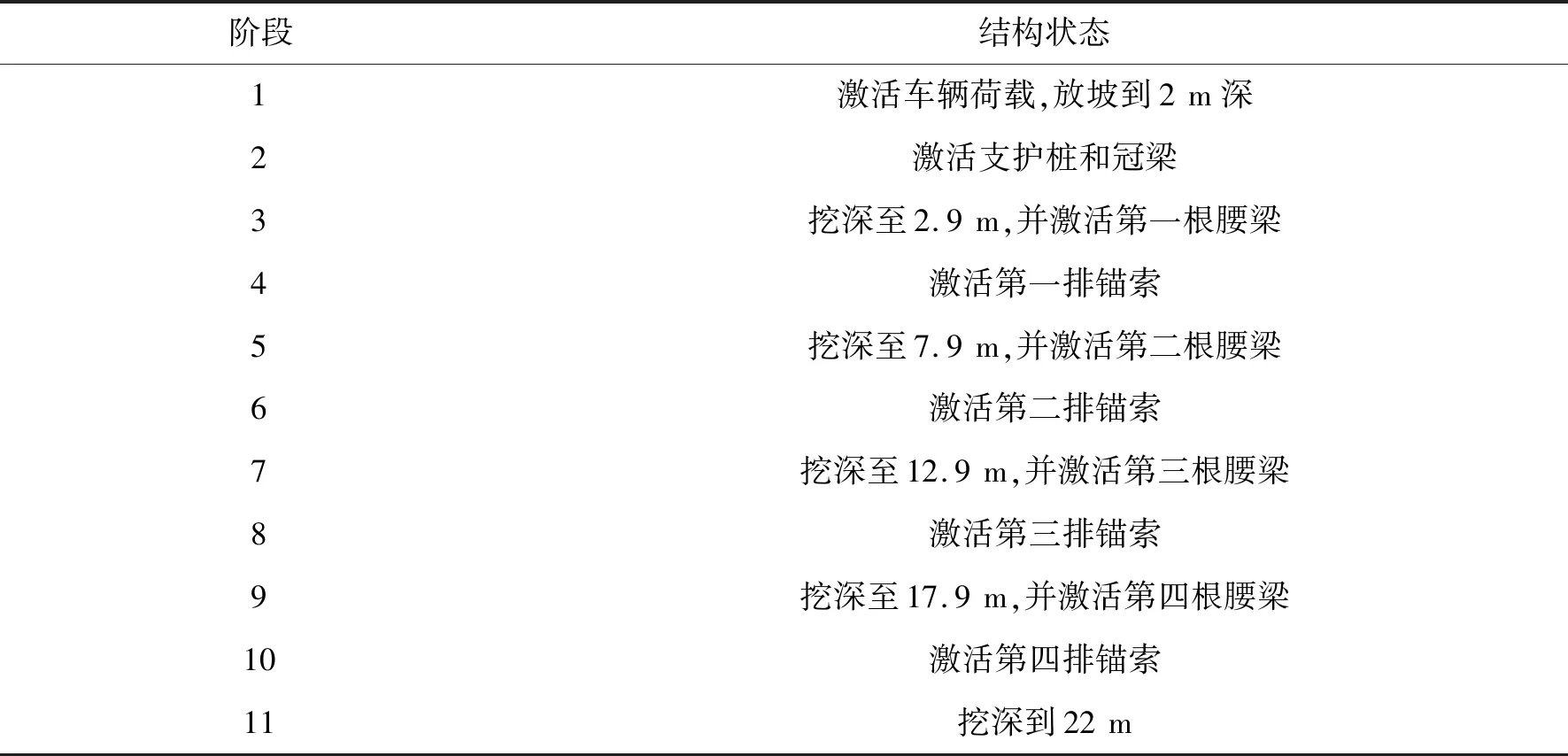
表4 模型计算步骤

表5 锚索轴力的对比表
4 模型结果的分析
4.1 桩顶位移的控制分析在3.2节模型的初始位置上,分别给M2施加200 kN、240 kN、280 kN、320 kN和360 kN的预应力,并分别计算该支护结构在地下水位8 m,6 m,4 m,2 m和0 m时的桩顶位移,如图5所示.

从图5中可以看到,随着所施加的M2预应力的增大,桩顶位移有相应的减小;在确定施加预应力大小的情况下,随着水位的增加,桩顶位移有相应增大,且在施加不同预应力的情况下,增大的速率基本相同;在水位一定的情况下,随着预应力的增大,可以使桩顶位移相应减小8.4%~10.7%.该结果表明,在M2的预应力适当增大的情况下,可以有效降低该支护结构的桩顶位移.夏晋华等人[10]的研究同样表明,预应力锚杆对限制基坑坑壁的侧移起着至关重要的作用.
4.2 锚索受力的变化分析图6和图7所示为对M2所施加的不同大小预应力,且在保持对M1、M3、M4施加预应力大小不变的情况下,分析了M1~M4在地下水位为0 m时(即桩顶位移最大时)的轴力大小变化情况.
图6的结果表明,在0 m水位下,随着所施加的M2预应力的增大,其本身的轴力亦随之增大,且M1的轴力值随之相对减小.图7的结果表明,在0 m水位下,所施加的不同大小的M2预应力对M3和M4的轴力影响较小,M1和M2的总体趋势如图8、图9所示.
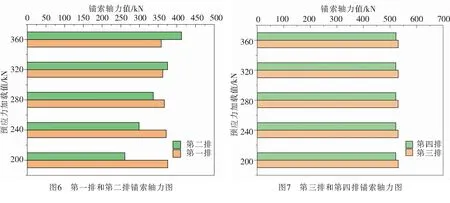
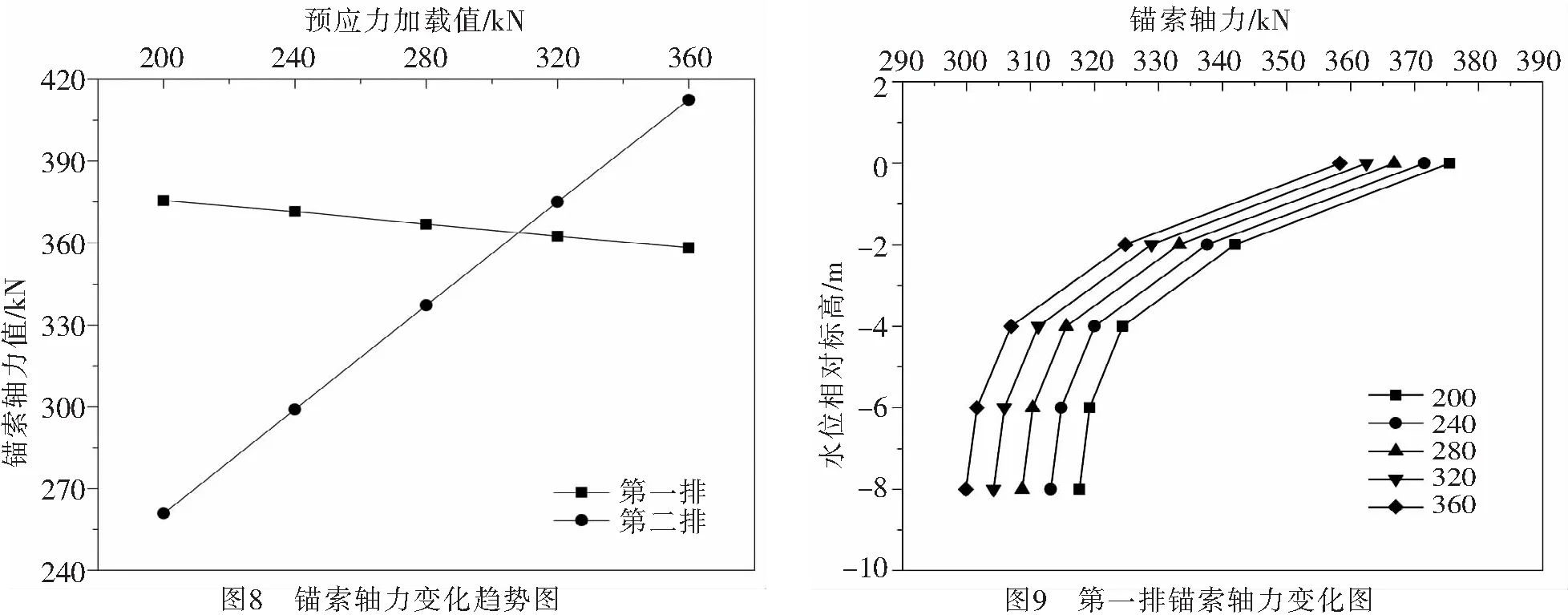
图8的结果表明,随着所施加的M2预应力的增大,在其他锚索所施加预应力保持不变的情况下,M2本身的轴力增大比较明显,同时M1有较缓慢减小的趋势.通过图8和图9可以得到,在0 m水位下,M2的预应力从200 kN增加到360 kN的过程中,可以使M1的轴力降低4.6%~5.6%.该结果表明,适当提高M2的设计荷载以符合水平土压力的分布规律,可以使M1和M2在相同配筋的情况下受力更加合理,同时还可以提高基坑的安全性.
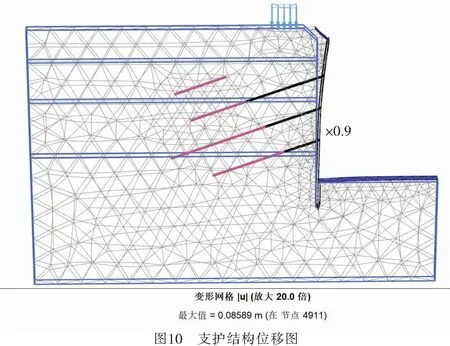
4.3 第一排锚索失效的影响在0 m地下水位的模型计算中,考虑到了水体上升可使土体抗剪能力降低和导致M1在支护结构中失去作用的情况,并分析了其失效后对支护结构的影响.在模型中将M1“冻结”后进行数值分析,其支护结构的桩顶位移如图10所示.结果表明,M1失效后位移由原来40 mm左右的最大位移发展到了85 mm以上的位移,超过了基坑安全的预警值,可以发现该基坑已有倒塌迹象.因此,锚索失效与基坑倒塌具有直接联系,同时也证明了锚索体系受力性能的合理性对基坑整体的安全性极其重要.
5 结论与建议
通过对广西某倒塌深基坑桩锚支护体系的数值模拟分析可以得到以下结论:
(1)当预应力锚索的受力分布规律与土压力分布包络值的趋势保持一致时,可有效降低支护结构的桩顶位移,同时可以使相邻锚索的受力更加合理,从而增强了整个桩锚支护体系的作用性能,以使得基坑的安全性得到提高.
(2)增加M2(第二排锚索)的预应力后,可以使M1(第一排锚索)和M2的受力更加合理,并使基坑的安全性得到提高,从而可以有效预防基坑倒塌的发生.
通过对该基坑倒塌案例的分析,对于桩锚基坑支护体系的设计建议如下:
(1)在软件计算结果中,锚索设计荷载应符合土压力的分布规律.
(2)考虑锚索预应力存在损失的情况,故应适当提高锚索的预应力,以保证其锁定荷载在合理的范围内.
(3)在深基坑及超深基坑中,在基坑弯矩较大的中上部区域,应锚索轴力的安全设计值范围.
