具有脉冲效应和Holling Ⅱ功能反应的治理害虫的Gompertz病毒病模型系统分析
2021-04-25郭俊荣金浩城
郭俊荣, 金浩城
(浙江农林大学 理学院,浙江 杭州 311300)
引言
害虫治理是农业生产中不可避免的一个问题。害虫对于农作物等经济作物的危害影响不容小觑。我国的农业生产中,常见的害虫多达八百余种,其中对于经济作物危害严重的种类则超过了二十余种。由于受到不可控因素的综合影响,一些曾经被有效控制的害虫再次开始影响农业生产生活,其次要的害虫种类危害程度加重,呈现出流行面积扩大、危害程度加剧、发生频率增多等趋势,对于农业生产生活构成极大的威胁[1-2]。
针对上述问题,本文构建并分析了一类具有脉冲效应和Holling Ⅱ功能反应函数的治理害虫的Gompertz病毒病模型,从分析结果中得到了一些有意义的结论。
1 模型建立
文献[3]中引入了如下的病毒传染病脉冲微分方程:
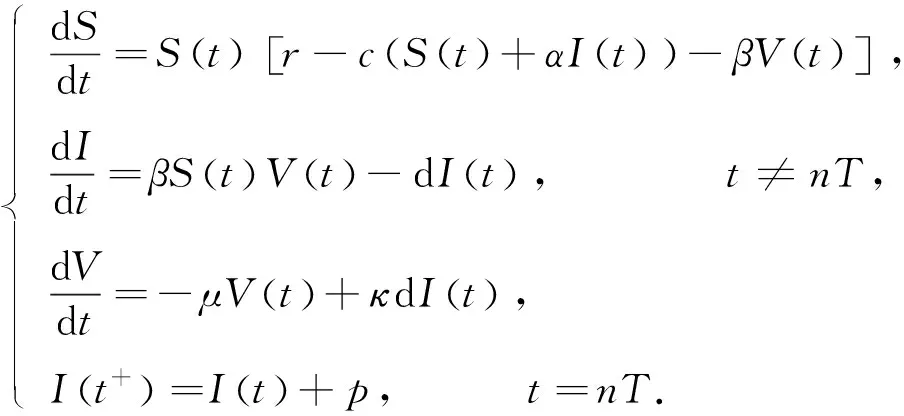
(1.1)
其中,所有参数都为正数。
Holling在文献[4]中提出了三种不同的功能反应函数来描述生物种群的捕食现象。在上述文献的基础上,本文构建了具有脉冲效应和Holling Ⅱ功能反应函数的治理害虫的Gompertz病毒病模型,基于病毒的生物控制策略的脉冲微分方程如下:
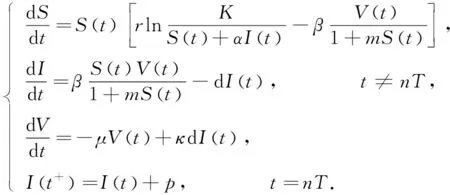
(1.2)
其中,S(t)代表易感类害虫,I(t)表示感染类害虫,V(t)表示病毒,r为内禀增长率,K为环境承载量,α≥0,β表示传染率,m≥0,d表示因病死亡率,μ表示病毒死亡率常数,κ表示病毒复制参数,p表示以常数连续投放染病的害虫。
2 模型分析结果
2.1 预备知识
下面给出本文中用到的一些引理及定理。
2.1.1 脉冲微分方程的Floquet理论
定义2.1.1对于以下的方程:
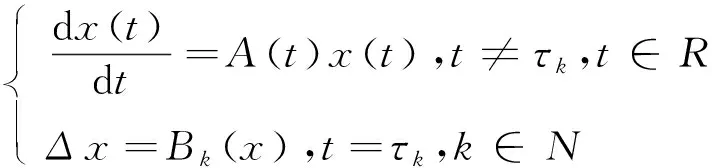
(2.1.1)
若有下列条件:
(a)A(·)εPCH(R,Cm×n)并且A(t+T)=A(t),t∈R;
(b)BkεCm×n,det(E+Bk)≠0,τk<τk+1(k∈N);
(c)存在取值q∈N,满足Bk+q=Bk,τk+q=τk+T;
则称(2.1.1)为线性T-周期脉冲微分方程。
定理2.1.1[5]若条件(a)、条件(b)、条件(c)成立,则(2.1.1)的基解矩阵可以表示成如下形式:
X(t)=Ø(t)eΛt(t∈R)
(2.1.2)
其中,矩阵Λ∈Cn×n是常值矩阵,矩阵Ø(·)∈PC1(R,Cn×n)是非奇异和T-周期的。
注释2.1.1根据2.1.1及条件(c)易知Floquet表达式(2.1.2)中的Ø(t)是一个Lyapunov矩阵,即满足以下条件:
(ⅰ)Ø(·)εPC1(R,Cn×n);
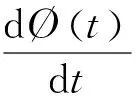
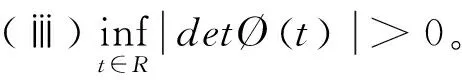
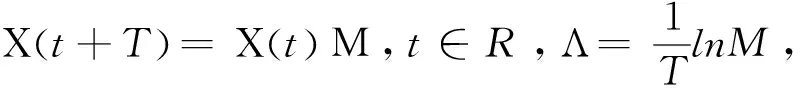
注释2.1.2可以证明系统(2.1.1)所有的单值矩阵都相似且有相同的特征根。
定理2.1.2[5]若条件(a)、条件(b)、条件(c)成立,则T-周期的线性脉冲微分方程(2.1.1)是:
(a)稳定的,当且仅当系统(2.1.1)的所有Floquet乘子μj(j=1,2,…,n)满足不等式|μj|≤1,而且|μj|=1的Floquet乘子μj重数均为1;
(b)渐近稳定的,当且仅当系统(2.1.1)的所有Floquet乘子μj(j=1,2,…,n)满足不等式|μj|<1;
(c)不稳定的,若存在某些jε1,2,…,n,有|μj|>1。
2.1.2 脉冲微分方程的比较定理
首先,定义如下函数集
定义2.1.3设V∈V0,则对于(t,x)∈(tk,tk+1]×Ω,脉冲微分方程的V(t,x)的右上导数定义为:
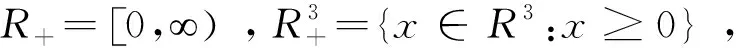
引理2.1.1设x(t)是系统(1.2)的解,并且满足初值条件x(0+)≥0,那么对所有的t≥0均有x(t)≥0。若x(0+)>0,则当t>0时,有x(t)>0。
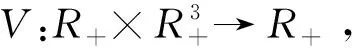
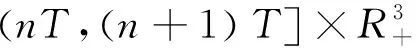
(2)V关于x是局部Lipschitz的。
则称V是属于V0类的,即V∈V0。
定理2.1.3[5-6]假设函数ω(t)∈PC1([0,∞),R)满足不等式
(2.1.3)
其中,f(t),g(t)∈PC([0,∞),R),fk>0,gk和ω0是常数(k=1,2,…),则对t>0有
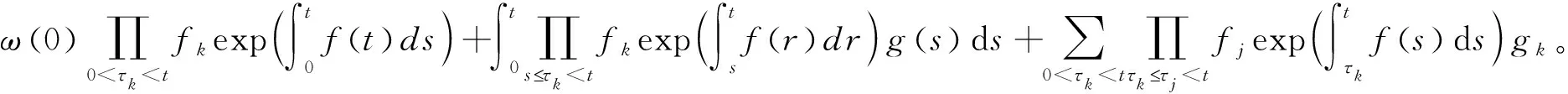
类似的,若不等式组(2.1.3)反向,则对t>0有
考虑下面的系统(2.1.4)
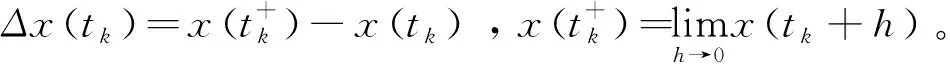
且假设其满足下列条件:
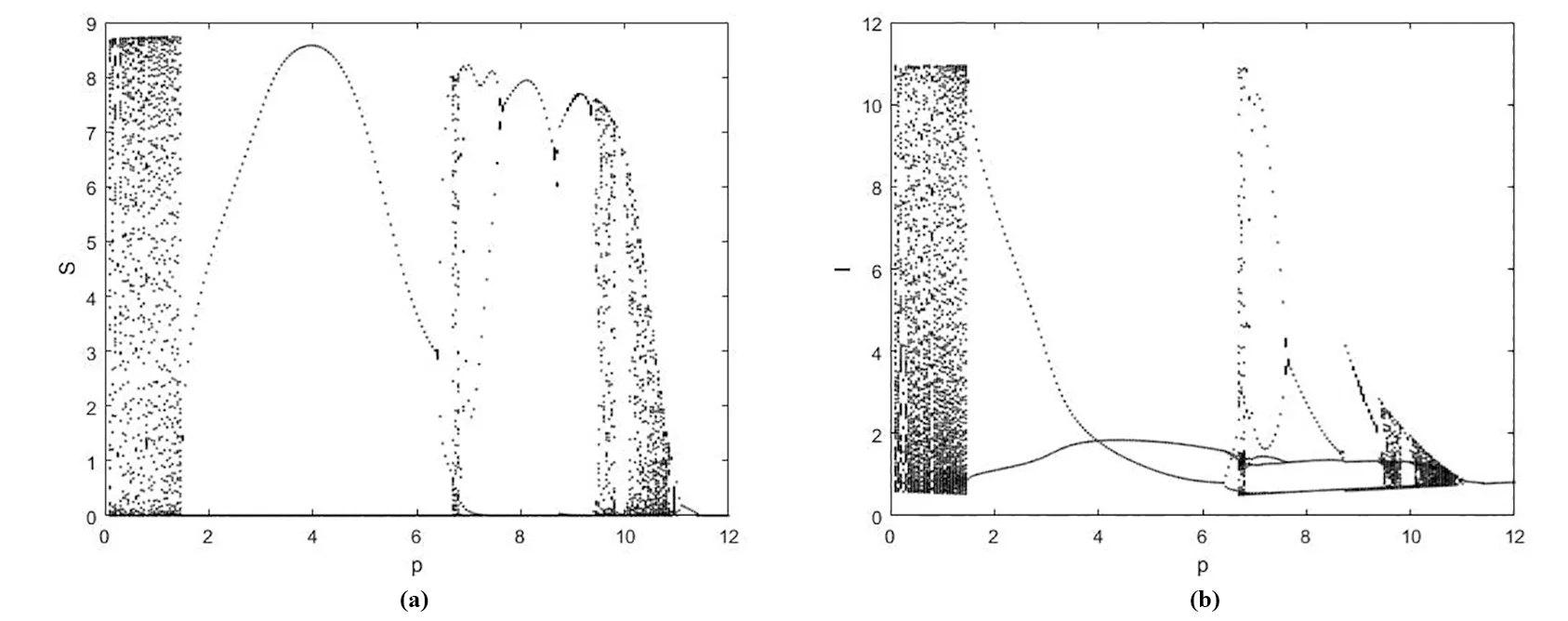
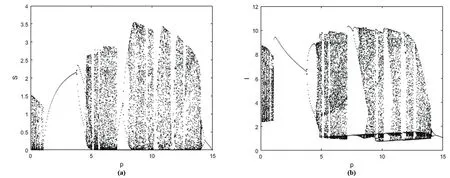
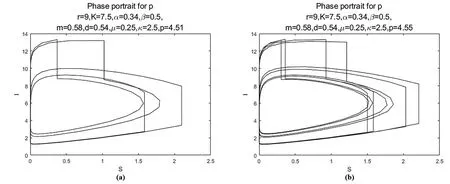
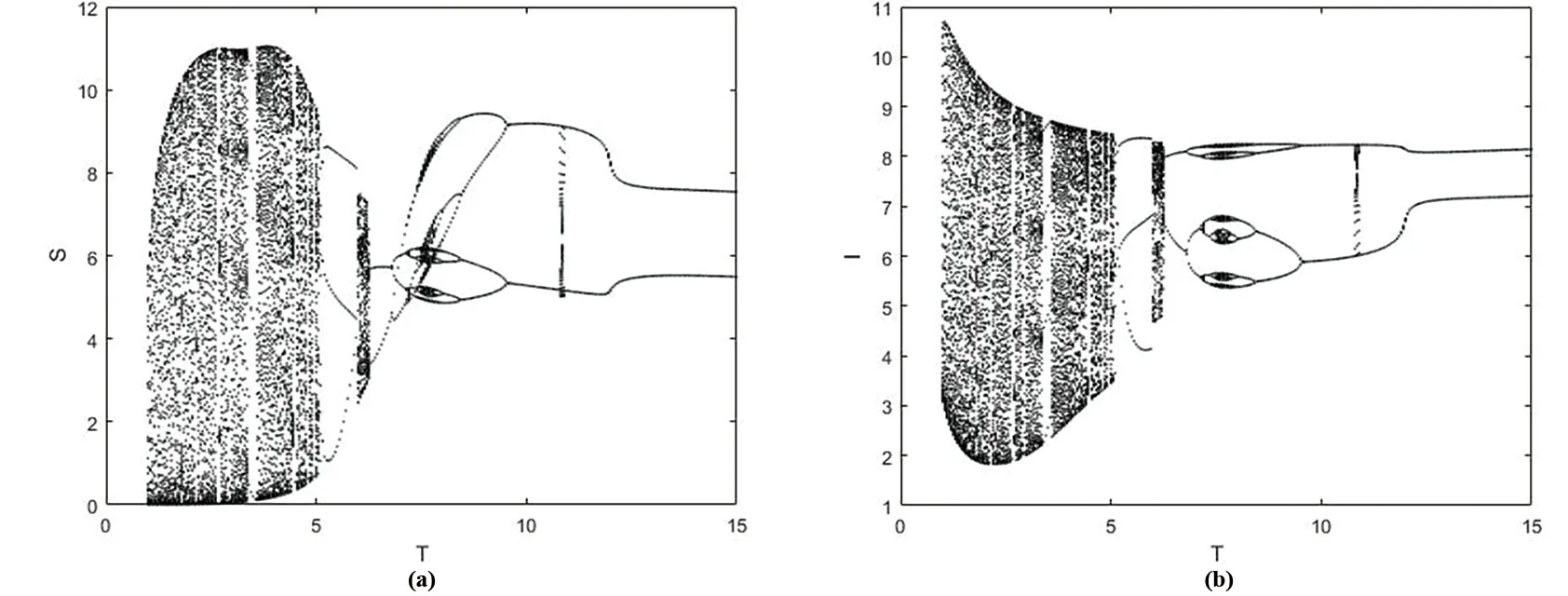
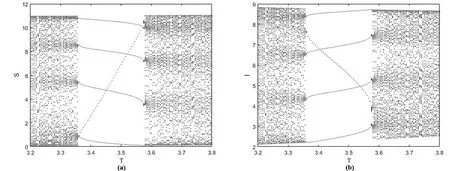
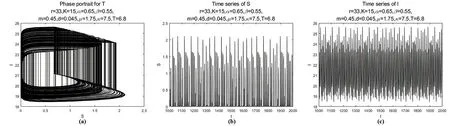
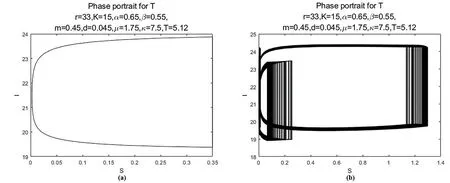
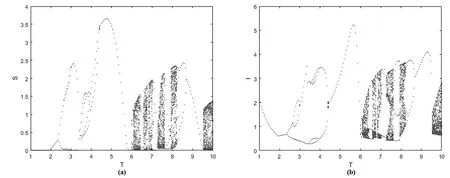
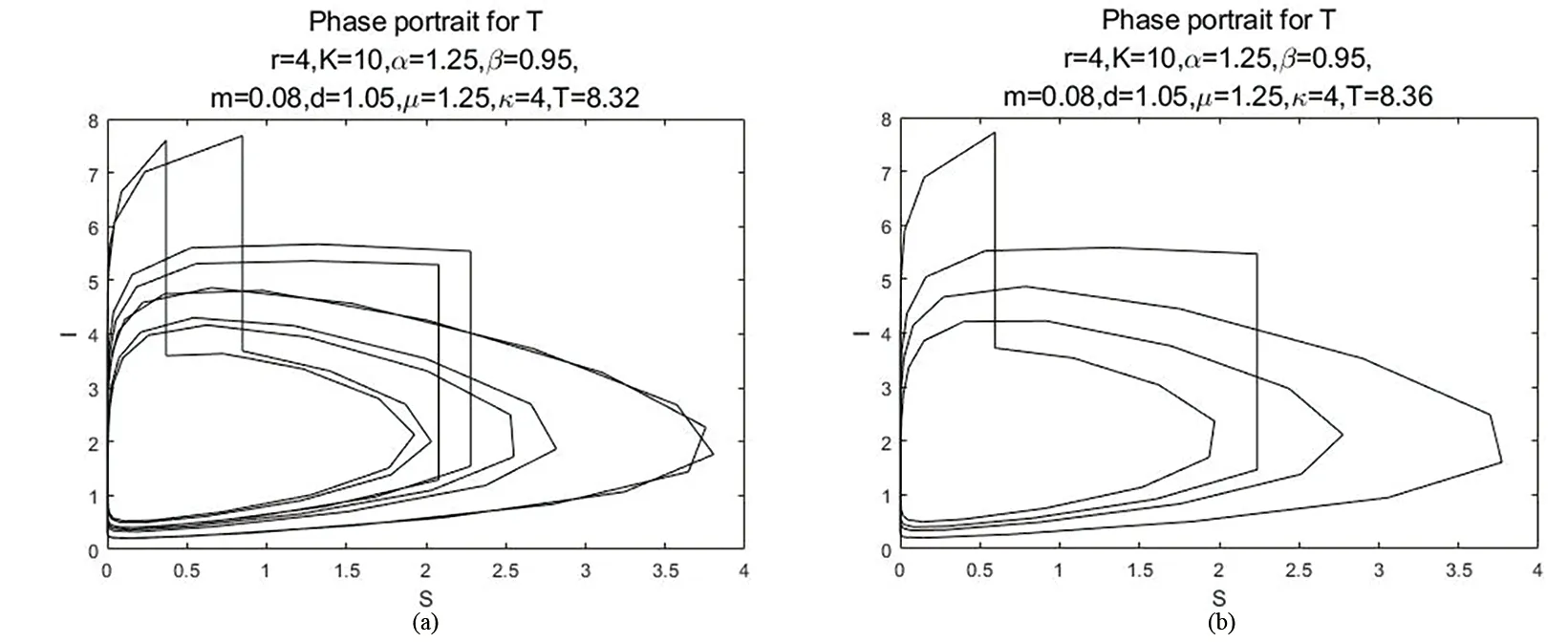
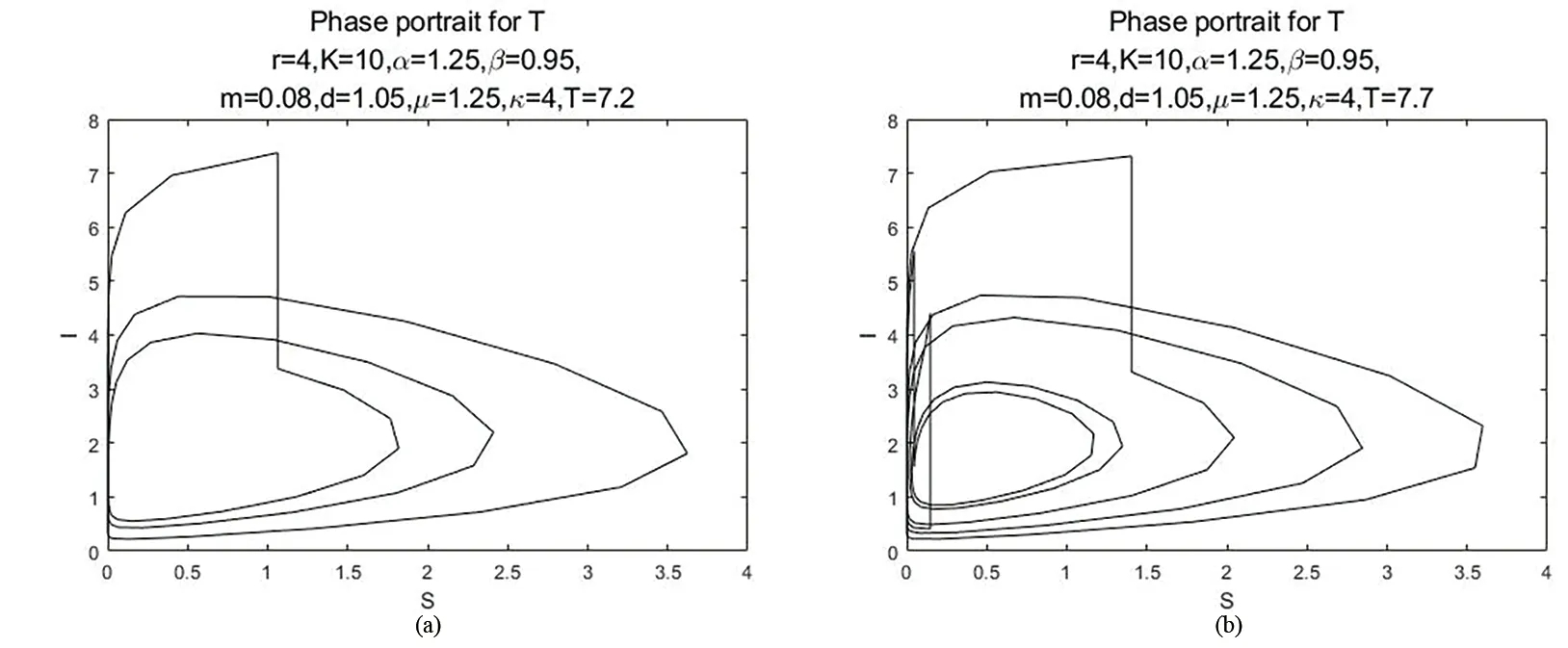
(1)0 (2)f:R+×RnRn在(tk-1,tk]×Rn,k∈N区域内是连续的,并且对任意k∈N,x∈Rn,lim(t,y)→(tk,x)f(t,y)=f(tk,x)存在; (3)Ik:RnRn 设g:R+×RnR+满足 定理2.1.4[7]假设V∈V0,且有下列不等式成立 (2.1.5) 其中g:R+×R+R满足(H),且φk:R+R+是单调不减的,设r(t)是下列方程在[0,∞)上的最大解 (2.1.6) 那么V(0+,x0)≤u0,由此可得V(t,x(t))≤r(t), 其中x(t)=x(t,t0,x0)是系统(2.1.4)在[0,∞)上的任意解。 定理2.1.4中的V,g均是标量函数,若为向量函数,并且g是拟单调不减的函数时,也可以得到相似的结论。 下面,对以下的系统(2.2.1)进行分析。 (2.2.1) 定理2.2.1对于系统(2.2.1)的解(S(t),I(t),V(t)),存在一个常数M>0,使得对于充分大的t,有S(t)≤M,I(t)≤M,V(t)≤M。 证明令W(t)=S(t)+I(t)+V(t), 其中,L≤min{μ,d-κd}。 于是 W′(t)+LW(t)≤(L+rlnK-rlnS(t))S(t)。 由上,则有 由上节中的比较定理和引理,可得 当t趋于无穷时,可推得: W(t)≤M,即S(t)≤M,I(t)≤M,V(t)≤M。 当S(t)灭绝时,可得到如下等式: (2.2.2) (2.2.3) 为了求出V(t),构造如下的g(t) g(t)=V(t)eμ(t-nT),t∈(nT,(n+1)T]。 另一方面, 综合上式可得: 易知,有唯一的正不动点, 系统(2.2.1)可扩展成如下的线性形式: (2.2.4) 本节利用数值模拟手段,通过以脉冲投放量参数p和周期T为分岔参数绘制分岔图以及模型系统的相图和时间序列图,可以研究脉冲投放量p,以及周期T这两个参数对上述系统(2.2.1)的内部动力学的影响。 对于捕食者投放量p,讨论以下两种情况。 情形一: 图1 系统的分岔图。r=6;K=10;α=0.5;β=0.65;m=1.25;d=0.55;μ=1.2;κ=9;T=5;p∈[0.1,12]。 由图1可知,系统在上述参数条件下,经历了比较复杂的过程:混沌→周期→具有周期窗口的混沌→周期。 情形二: 图2 系统的分岔图。r=9;K=7.5;α=0.34;β=0.5;m=0.58;d=0.54;μ=0.25;κ=2.5;T=5;p∈[0.1,15]。 图3 倍周期分支过程。(a)p=4.51时系统4T-周期解的相图;(b)p=4.55时系统8T-周期解的相图。 图4 奇怪吸引子。(a)p=6.9时系统的相图;(b),(c)p=6.9时系统关于S,I的时间序列图。 从上述分析的结果可以看出,在不同的参数条件下,系统将出现不同的动力学行为。情形三中,随着脉冲投放量p的增加,系统(2.2.1)经历了复杂的动力学行为。当p∈[0,1.05]时,系统呈现混沌状态,当p∈[1.05,3.66]时,S,I,V以稳定的T周期解形式共存,当p>3.66,系统开始进入倍周期分支,继续增加p的值,T-周期解不再稳定,随后变为2T-周期解;当p>4.41时,系统开始由2T-周期解进入4T-周期解,当p>4.44时,系统以4T-周期解稳定存在;p>4.58时,系统又开始呈现混沌状态。当p=6.9时,可以看到系统的一个典型混沌吸引子。继续增加p的值,当p=7.122时,系统呈现拟周期振荡。当p>7.125时,系统出现周期瀑布;当p>14.12时,系统进入4T-周期解;当p>14.15时,系统进入2T-周期解;当p>14.35时,系统又完全收敛到T-周期解。在整个p值增大的过程中,可以看到系统经历周期到倍周期分支到混沌,以及重新恢复为周期的过程。 对于T,讨论以下三种情况。 情形一: 图5 系统关于T的分岔图。r=2.4;K=15;α=0.6;β=0.5;m=0.95;d=0.6;μ=1.05;κ=2.4;p=2.5;T∈[1,15]。 图6 局部放大图。T∈[3.2,3.8]。 从图5和图6可以看到,系统在此条件下具有丰富的动力学行为。当T<5.145时,系统处于混沌状态,且伴有周期窗口。当5.145 情形二: 图7 奇怪吸引子。(a)T=5.3时系统的相图;(b),(c)T=5.3时系统关于S,I的时间序列图。 图8 当T=5.12时,T-周期解与混沌吸引子共存。(a)初始值为S=3;I=0.1;V=0.01的解,最终趋于一个T-周期解; 从上述数值结果可知,在此参数条件下,系统的动力学行为更为复杂。图7给出了T=5.3时的一个奇怪吸引子。由图8可知,T=5.12时,系统具有一个典型的特征,即不同的吸引子可以共存。 情形三: 图9 系统关于T的分岔图。 图10 半周期分支过程。(a)T=8.32时系统8T-周期解的相图;(b)T=8.36时系统4T-周期解的相图。 图11 周期窗口。(a)T=7.2时系统3T-周期解的相图;(b)T=7.7时系统5T-周期解的相图。 由图9可知,系统经历了如下的过程:周期→倍周期分支→混沌和不唯一的动力学行为。图10展示了系统的一个半周期分支过程,图11给出了T=7.2和T=7.7时系统的两个周期解。 从上述分析结果可以看出,随着T的增加以及初始值的不同,系统的解发生了完全不同的变化,说明系统对初始值非常敏感,且具有复杂的动力学行为。针对多种群系统,引入病虫,即加入脉冲控制量之后,会改变系统的状态,使得系统呈现难以预测的变化,从而可以研究控制系统的变化,使得系统在适当的参数条件下存在稳定的周期解。即在种群中,可以使得易感害虫和染病害虫共存,这在生态系统中具有一定的生物意义。 本文针对具有脉冲效应和Holling Ⅱ功能反应的Gompertz治理害虫的病毒病模型的数值分析表明,脉冲投放量p以及周期T等参数会影响系统的动力学行为。以脉冲投放量p以及周期T作为分岔参数得到分岔图,由可视化图形结果表明,系统具有复杂的动力学行为。其中,图2、图5、图9等分岔图显示了系统具有倍周期分支,半周期分支,混沌,周期窗口等复杂的结构,这些表明了系统的动力学行为受脉冲量p以及周期T影响。上述对系统(2.2.1)的动力学分析,旨在通过对模型的动力学分析,得到一些对治理害虫有意义的数学理论上的指导和帮助。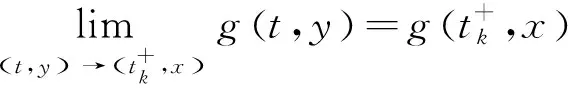
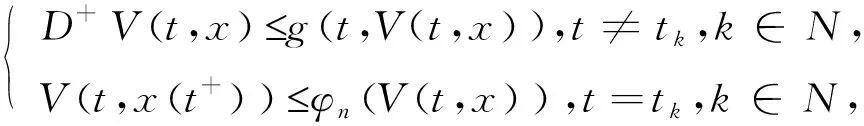
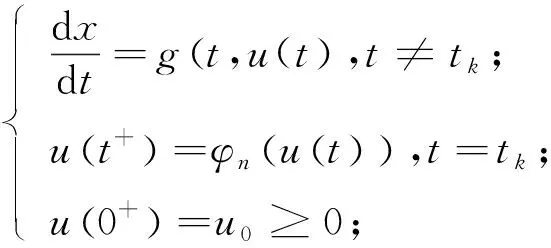
2.2 主要结果
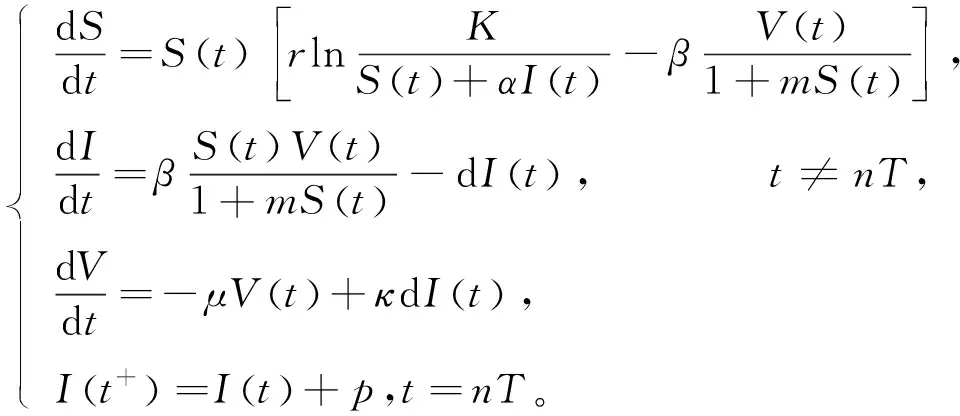
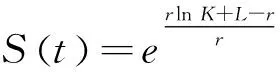
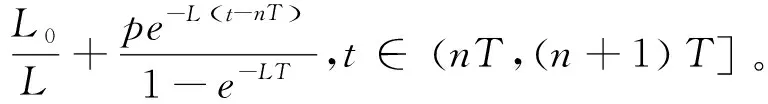
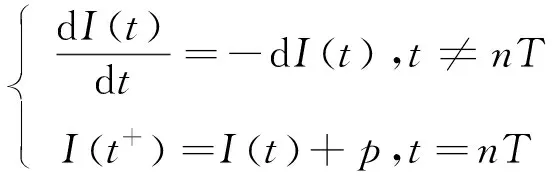
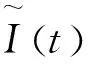
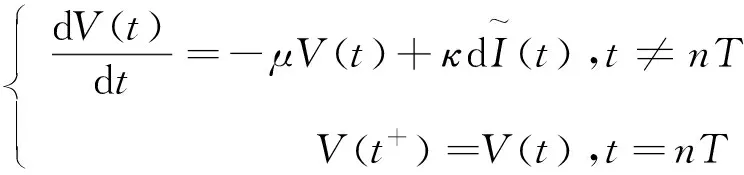

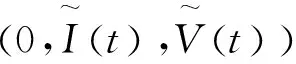
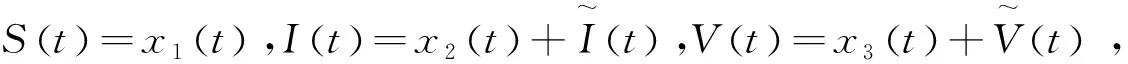
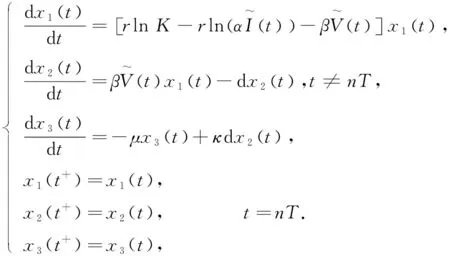
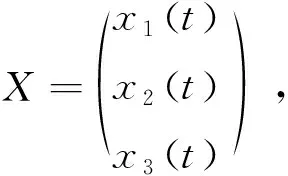
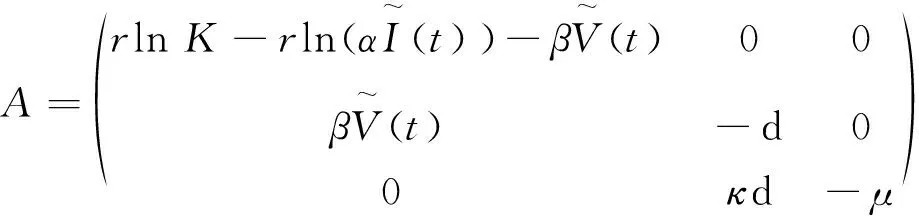
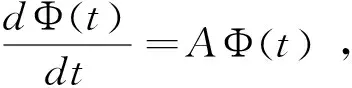
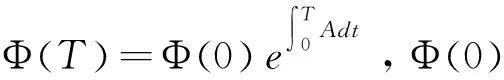

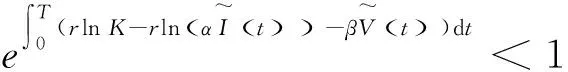
3 数值分析

4 结束语
