常州市能源消费与经济增长探究
2021-04-25徐文涛
徐文涛
(南京财经大学经济学院,江苏 南京210023)
一、 引言
能源是人类社会以及经济发展的重要基础,是关系到国家命脉的战略资源。 一方面,现代社会任何的经济活动都离不开能源的供给,一个经济体的能源消费总量可以很大程度上反映其经济体量;另一方面,所有生产活动对能源的需求又会带来能源市场的波动,对能源的价格及生产产生重大影响。 理论上,能源消费与经济增长之间存在密切联系。 常州市作为“苏锡常”都市圈的成员之一,经济发展水平长期位于江苏省前列。 同时,常州市也是能源消费大市,2018 年市全社会用电量达到455.03 亿千瓦时,是省内第四大用电城市。研究其能源消费和经济发展之间的关系,对未来经济发展和能源战略政策制定具有重要的意义。
从20 世纪70 年代开始,国外学者便开始了有关能源与经济增长之间关系的实证研究,但是长期以来关于二者之间的关系一直无法达成共识。 研究所采用的模型、样本数据和地区的不同都会导致不一样的结论。 J.Kraft 和A.Kraft(1978)利用美国二战后1947~1974 年度的GEI(gross energy inputs)和GNP(gross national product)数据,借鉴Sims(1972)单向因果检验的方法进行的研究表明,存在经济增长到能源消费的单向因果关系,且经济增长可以推动能源消费;然而,Akarca 和Long(1980)认为J.Kraft 和A.Kraft 的研究因为采用了发生经济萧条、石油禁运以及能源价格暴涨的1970 和1973~1974 年的数据而出现了“伪回归”的结果,并采用更短的时间序列数据进行实证检验加以验证,结果无法得出经济增长影响能源消费的结论,从而证明了自己的观点。 Tugcu等(2012)通过自回归分布滞后模型对G7 国家1980~2009 年的数据进行了实证分析,发现无论是可再生还是不可再生能源长期以来均对经济增长产生重要的推动作用,且在经典生产函数的情况下经济增长与能源消费能够相互影响;而Mutascu(2016)通过扩大样本容量,采用1970~2012 年数据,并用面板协整模型对G7 国家进行检验,结果却发现不同国家能源消费与经济增长之间的关系呈现出明显不一致性。 上述研究结果表明,即使针对同一研究对象,能源消费与经济增长之间的关系也可能会因为样本、模型的不同而产生完全不同的结论。
我国相关研究是从20 世纪80 年代中后期开始的。 赵丽霞和魏巍贤(1998)将能源作为投入要素引入C-D 生产函数,建立VAR 模型,考察我国1978 ~1996 年GDP、劳动力投入、资本投入及能源消费数据,发现我国在这一时期能源消费与经济增长正相关;林伯强(2003)认为由于煤炭私采滥挖与原油和成品油走私非常猖獗,我国能源消费总量被严重低估,因此以计算机直接读出的电力消费数据代替总能源消费数据进行研究,通过误差修正模型发现,我国GDP、资本投入、劳动力投入与电力消费之间存在长期均衡关系。 随着研究的深入,一些学者逐渐认识到线性假设的局限性,尝试以非线性模型解释能源消费与经济增长之间的关系。 赵进文和范继涛(2007)在借鉴Granger 和Terasvirta(1993)LSTR 模型的基础上,对我国1953 ~2005 年GDP 与一次能源消费量进行了实证分析,发现经济增长对能源消费存在非线性影响;隋建利等(2017)创造性地将能源消费与经济增长之间的时变因果关系划分为:能源消费和GDP 相互作用、能源消费单向作用于GDP、GDP 单向作用于能源消费和GDP 与能源消费之间无因果关系4 个区制,基于非线性马尔科夫区制转移因果模型,分别测度煤炭、石油、天然气和电力消费与经济增长之间关系的区制转移概率,结果显示能源消费与经济增长之间的关系存在显著的能源异质性。
论文将借鉴曾胜和黄登仕(2009)的做法,采用生产规模报酬不变的C-D 生产函数测算的常州市能源消费对GDP 的贡献量作为产出指标,同时将煤炭、天然气、汽油与电力消费作为投入指标,逐年测算2015~2018 年的能源效率;随后,分别使用2015 ~2018 年常州市下辖6 个区县的面板数据与1980~2018 年常州市的时间序列数据进行VAR 模型回归,研究能源消费与经济增长之间的因果关系。
二、 常州市各地区能源效率现状
从图1(a)可以看出以电力消费为代表的常州市能源消费量与GDP 几乎保持相同的增长率,说明常州市的能源消费量与GDP 有着较为接近的增长趋势。 从图1(b)可以看出,虽然常州市的能源消费与GDP 保持着几乎相同速率的增长,但是常州市GDP 的增长量要远远高于能源消费的增长量。从单位GDP 的能源消费角度来看,常州市的单位GDP 能源消费是长期下降的,说明自改革开放初期以来常州市在提高生产率和资源利用率方面取得了巨大进步。
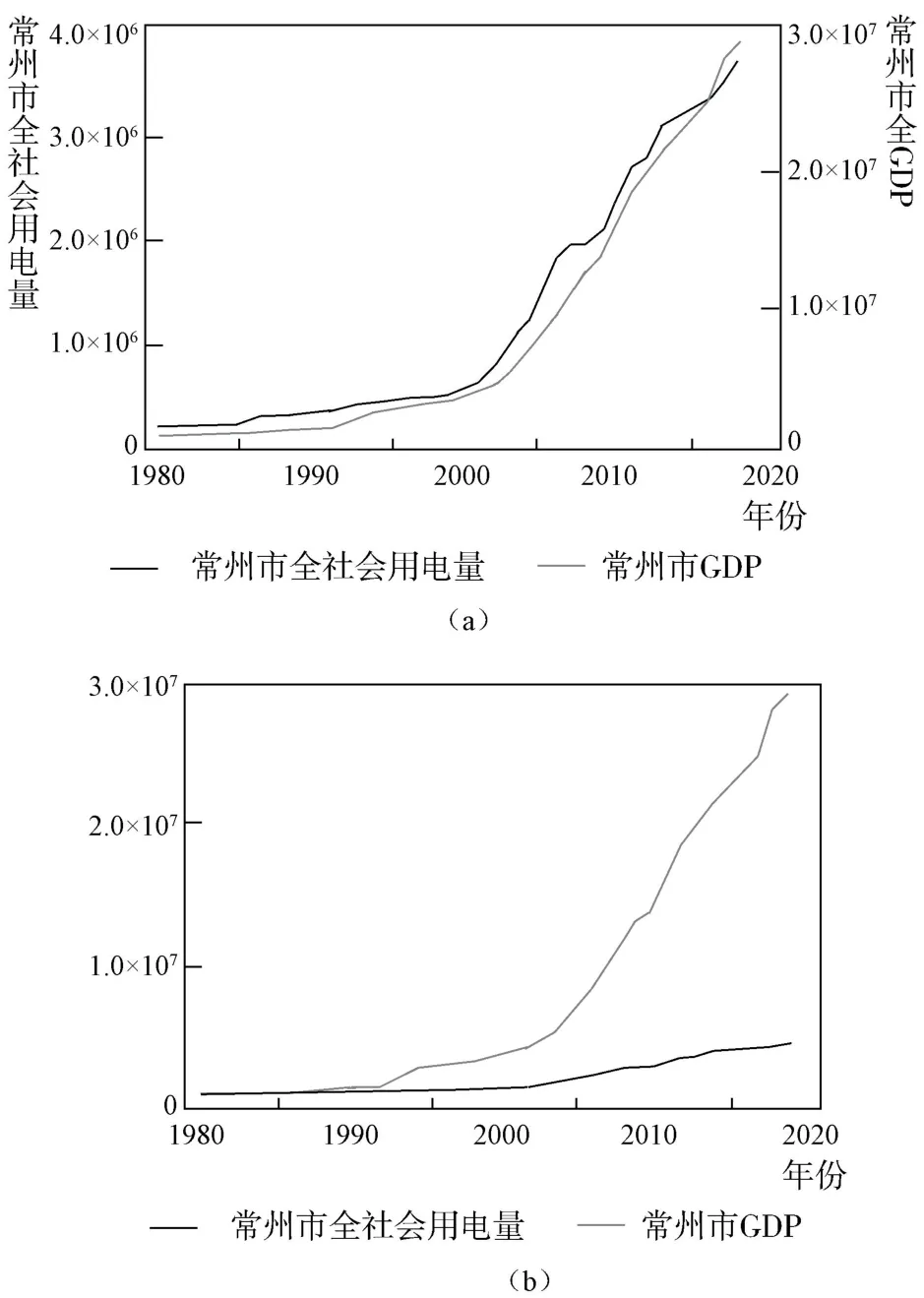
图1 1980~2018 年常州市全社会用电量和GDP 增长趋势图
由于上述只是基于图表的粗略分析,且单位GDP 的能源消费缺乏对GDP 中能源贡献率的准确测度,因此论文将借鉴曾胜和黄登仕(2009)的做法,将能源看作生产投入要素之一,基于C-D 生产函数测度能源消费对GDP 增量的贡献,并利用DEA 方法研究常州市能源利用效率。
假定GDP、资本、劳动力、能源消费满足C-D 生产函数,即:
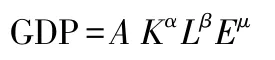
其中,K表示全社会固定资产投资,L表示就业人数,E为能源消费总量,α、β、μ分别表示资本、劳动力和能源对GDP 的贡献率。 通过对函数两边求对数使之线性化,并对时间t求导有:


表1 C-D 函数回归结果

由回归结果可以看出,资本、能源系数均符合预期且显著,只是L 的数值为负且不显著,原因可能是经济、资本、能源消费增长都较快,而劳动力增长缓慢,并且增长率还出现下降的趋势。 根据回归结果可得:
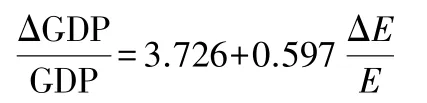
说明能源消费每上升1 个百分点,经济增长将上升0.597个百分点。 据此可以测算出经济增长中能源消费增长的贡献量。 以能源消费贡献的经济增长量作为产出,以煤炭、天然气、汽油和电力消费作为投入,利用DEA 方法对2015 ~2018 年常州市下辖6 个区县生产的能源效率进行测度。
非参数估计的DEA 方法是运筹学的一个新的研究领域,用于评价决策单元(DEA)的相对效率,其目的就是构造非参数的包络生产前沿面。 生产前沿面描述在当前技术水平下有效率的投入产出向量,即给定投入和其他产出不变时一种产出的最大值,有效点位于生产前沿面上,无效点位于生产前沿面的下方。 由于仅使用了2015 ~2018 年6 个区县的数据测量能源效率,时间较短,因此论文采用假定规模报酬不变的CCR 模型进行测度。 模型如下:


表2 DEA 测度结果
从测度结果可以发现,常州市下辖6 个区县,2015~2018年除了新北区以外均达到了DEA 有效,即均处于生产前沿面之上。 回归结果说明,一方面,金坛区、武进区、天宁区、钟楼区和溧阳市近几年生产的能源利用效率水平比较接近,新北区能源利用效率相比较而言处于较低水平,这可能是因为新北区和其他区县相比较存在更多的高能耗型化工企业,且许多企业规模较小、技术落后、单位产值能耗较高;另一方面,新北区近年能源利用效率有了较快的提升,这可能是由于为了贯彻省委、省政府《关于印发“两减六治三提升”专项行动方案的通知》,省政府办公厅《关于开展全省化工企业“四个一批”专项行动的通知》,常州市新北区自2017 年起开始实施了减少落后化工产能暨化工企业“四个一批”专项行动。
为了进一步分析常州市整体能源消费与经济增长之间的关系,利用2015~2018 年常州市下辖的6 个区县一级的面板数据和1980~2018 年常州市的时间序列数据分别进行实证研究。
三、 常州市经济增长与能源消费的实证分析
论文选取2015 ~2018 年常州市下辖的6 个区县一级的工业综合能源消费(ICEC)和工业产值(IOV)数据,对能源消费与经济增长之间的关系进行实证分析。 还选取1980 ~2018 年常州市工业用电量(IELC)与全市工业产值(CIOV)数据建立时间序列数据对回归结果加以验证。 其中县区一级的综合能源消费数据的单位为吨标准煤,常州市工业用电量数据单位为万千瓦时,工业产值数据均为万元。 以上数据均取自历年常州市统计局公布的《常州市统计年鉴》。
(一)面板数据
首先对2015~2018 年金坛区、武进区、新北区、天宁区、钟楼区和溧阳市的工业综合能源消费与工业产值数据进行平稳性检验。 由于论文采用的面板数据时间较短,便没有对数据滞后平稳性进行检验。 在LLC 检验中,无论是工业综合能源消费(ICEC)还是工业产值(IOV)都强烈拒绝“存在单位根”的原假设,因此LLC 检验通过。 由于LLC 要求每位个体具有相同的自回归系数,这样的假设对于金坛区、武进区、新北区、天宁区、钟楼区和溧阳市可能过强。 并且由于截面与时间序列均较短,为避免检验结果产生误差,论文对面板数据进行了IPS 检验。 结果显示,在更为严格的IPS 检验中,工业综合能源消费(ICEC)和工业产值(IOV)统计量分别为-2.9212和-2.0201,且P值分别为0.0017 和0.0217——强烈拒绝“存在单位根”的原假设,所以可以认为该面板数据中不存在单位根。
由于两个变量均具有平稳性,可以进一步对其进行因果关系检验。 检验结果如表3:

表3 格兰杰因果检验
由检验结果可以看出,在10%的显著性水平下,“工业综合能源消费(ICEC)不是工业产值(IOV)的格兰杰原因”的原假设被强烈拒绝,而并不能显著拒绝“工业产值(IOV)不是工业综合能源消费(ICEC)的格兰杰原因”的原假设。 因此,根据检验结果可以认为在2015 ~2018 年常州市下辖六个区县的能源消费与经济增长之间存在单向的因果关系,能源消费是经济增长的格兰杰原因。
为了进一步探讨能源消费与经济增长的关系,论文采用面板VAR 模型对工业综合能源消费(ICEC)和工业产值(IOV)两个变量进行回归分析。 在进行回归之前先应确定最优滞后阶数,论文分别采用AIC、BIC 与HQIC 3 个准则对滞后期做了检验。 结果根据AIC、BIC 和HQIC 准则,滞后1 阶均是最优的,因此可以认为面板VAR 模型中滞后阶数应为1阶。 由于面板时间序列较短且6 个区县差别较小,可以认为不存在个体与时间固定效应,因此构建VAR 回归模型如下:
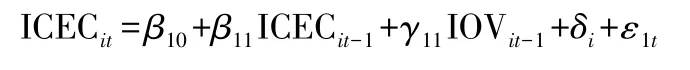

其中,IOVit和ICECit分别表示第i个区县、第j年的工业产值和工业综合能源消费量。 回归结果如表4 所示:

表4 回归结果
由回归结果可以看出,工业能源消费自回归系数为0.735,显著小于1,而且IOV 的自回归系数并不显著,再次证明了上述ICEC 和IOV 满足平稳性的结论。 ICEC 对IOV 的回归系数并不显著,但是IOV 对ICEC 的回归系数为2.674571,且可在5%的显著性水平下拒绝原假设,说明确实存在ICEC 对IOV 的单向因果关系,并且能源消费对产值增加存在显著的推动作用。 对于上述模型回归结果可以做这样的解释:在样本范围内,上一年的工业综合能源消费每增加1 吨标准煤,第二年的工业产值将上升大约2.34 万元。
(二)时间序列数据
为了避免面板数据样本太小导致回归结果的偶然性,论文采用常州市1980~2018 年的时间序列数据进行实证研究。 首先,对常州市工业用电量(IELC)与市工业产值(CIOV)两个变量进行平稳性分析。 通过Schwert(1989)建议的最大滞后阶数pmax=[12×(T/100)1/4]可知,IELC 和CIOV 的最大滞后阶数约等于9。 确定最大滞后阶数后,对IELC 进行ADF 检验。 由检验结果可知,9 阶滞后项在10%的水平下显著地不等于0。 且统计量Z(t)无法在10%的水平上拒绝存在单位根的原假设(0.550>-2.625),同时P值为0.9863。 因此可以认为IELC 含有最大滞后8 阶的单位根。 接下来,对CIOV 进行ADF 检验。 由于CIOV 的9 阶滞后项无法在10%的水平下显著地不等于0,因此又对CIOV进行了最大滞后阶数为8 的ADF 检验。 检验结果显示,8阶滞后项可以在5%的水平下显著地不等于0,且Z(t)统计量为0.955,P值为0.9938。 因此可以认为CIOV 含有最大滞后7 阶的单位根。 由于IELC 与CIOV 均存在单位根,不满足平稳性条件,对其进行对数化处理,得到lnIELC 与ln-CIOV 序列(以下简称LIELC 和LCIOV)。 由于经过对数化处理后的能源消费数据与经济增长数据仍然具有明显的时间趋势性,可初步判断不满足平稳性条件。 针对LIELC 和LCIOV 的平稳性,可以进一步进行DF-GLS 检验。 根据检验结果,从1 阶至9 阶滞后,LIELC 均无法在10%的水平上拒绝“存在单位根”的原假设,因此我们可以判定LIELC 依然不满足平稳性条件。 接下来,对LCIOV 的DF-GLS 检验,结果显示从1 阶至9 阶滞后,LCIOV 依然无法在10%的水平上拒绝“存在单位根”的原假设,因此可以判定LCIOV 依然不满足平稳性条件。 LIELC 与LCIOV 依然不满足平稳性条件。 除此之外,通过LIELC 和LCIOV 的协整分析发现无法在5%的显著性水平上拒绝“协整秩为0”的原假设。综上所述,得将LIELC 与LCIOV 进行差分,得到dLIELC 和dLCIOV,并进一步检验其平稳性。 从单位根检验结果可知,dLIELC 和dLCIOV 的检验统计量均小于5%的临界值,故可在5%的水平上拒绝“存在单位根”的原假设。 由于dLIELC和dLCIOV 均满足平稳性条件,可以对其进行格兰杰因果检验。 在进行格兰杰因果检验之前,需要根据信息准则对dLIELC 和dLCIOV 模型阶数进行确定。 结果显示,虽然基于AIC 准则,需要滞后9 项,但是根据FPE、HQIC 与SBIC准则,只需要滞后2 阶。 因此取滞后阶数为2 进行格兰杰因果检验。 根据滞后2 阶的格兰杰因果检验结果可得表5:

表5 格兰杰因果检验
从格兰杰因果检验结果可以看出,可以在10%的显著性水平上拒绝dLIELC 不是dLCIOV 的格兰杰原因原假设,同时无法拒绝dLCIOV 不是dLIELC 的格兰杰原因原假设。 可以构建VAR 模型如下:
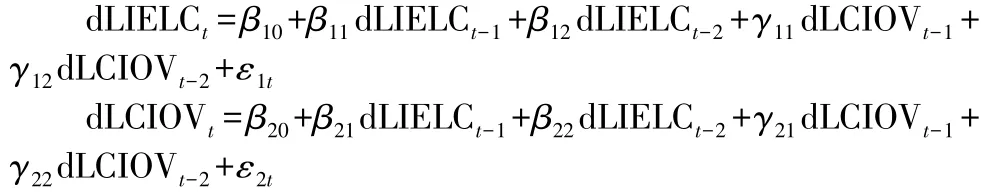
最后,对dLIELC 和dLCIOV 进行VAR 回归,结果如表6所示:

表6 VAR 回归结果
回归结果可以看出,滞后一阶的dLIELC 对dLCIOV 具有显著的推动作用,可以在1%的水平上拒绝原假设,因此可以说dLIELC 确实是dLCIOV 的格兰杰原因,符合格兰杰因果检验的结论;在10%的显著性水平上可以拒绝“dLCIOVt-1不会影响dLIELCt”的原假设,说明dLCIOV 可以在一定程度上影响dLIELC。 但是由于无法在5%的显著性水平上拒绝,因此可以认为dLIELC 和dLCIOV 之间的关系还是以dLIELC 推动dLCIOV 为主。 由回归结果可得以下两式(个别不显著的变量省略):

由上述方程组可知,常州市工业产值与工业用电量互相影响。 一方面,滞后1 期的工业产值对数的上升会推动工业用电量对数,滞后2 期的工业产值对数上升会降低工业用电量对数;另一方面,滞后1 期与滞后3 期的工业用电量对数会推动工业产值对数上升,滞后2 期的工业用电量会降低工业产值对数。 就时间序列而言,常州市存在经济增长与能源消费的双向因果关系,且影响的方向会随着滞后期的不同发生改变。
从面板数据来看,常州市各区县的能源消费对经济增长起促进作用,具体而言,上一年的工业综合能源消费每增加1吨标准煤,第二年的工业产值将上升大约2.34 万元。 从时间序列的回归结果可以看出常州市能源消费与经济增长长期以来互相影响,且根据滞后期的不同,能源消费与经济增长之间的关系会发生变化,具体而言:滞后1 期的经济增长会促进当期能源消费;滞后1 期的能源消费会促进当期的经济增长;滞后2 期的能源消费会抑制当期经济增长;滞后2 期的经济增长会抑制当期能源消费。 综上所述,短期内常州市以及下辖6 个区县的能源消费可以促进经济增长;长期来看,整个常州市的能源消费与经济增长之间存在具有时间异质性的双向因果关系。
四、 常州市能源效率与经济高质量发展对策研究
论文以柯布—道格拉斯生产函数所测算的常州市能源消费对经济增长的贡献量作为产出指标,以煤炭、天然气、汽油与电力消费作为投入指标,逐年测度了2015~2018 年的能源效率;随后,通过使用2015 ~2018 年常州市下辖6 个区县的面板数据与常州市1980 ~2018 年的时间序列数据分别进行VAR 模型的回归研究,实证分析能源消费与经济增长之间存在的因果关系。 通过研究常州市能源利用效率现状和分析能源消费与经济增长关系得出如下结论:第一,由于集中存在大量高能耗、规模小、缺乏技术的小型化工企业,常州市新北区的能源效率较其他五个区县低;第二,由于实施了减少落后化工产能暨化工企业“四个一批”专项行动,常州市新北区的能源效率2017 年起有了显著提升;第三,常州市下辖6 个区县均存在能源消费促进经济增长的作用机制;第四,常州市的经济增长与能源消费长期以来存在具有时间异质性的双向因果关系。
综合以上分析讨论,结合常州市能源消费与经济增长的具体情况,论文就促进常州市能源效率提高与经济高质量发展提出如下建议:
第一,提高能源利用效率。 由于存在大量规模较小、技术落后、能耗较高的化工企业,新北区能源效率水平较低,因此,应该采取相应措施提升新北区能源利用率,包括:整顿不符合规定的化工企业;合理引导先进化工企业向落后化工企业的技术转移;加大化工企业技术研发和升级投资的扶持力度。
第二,改善能源消费结构。 由于常州市存在能源消费促进经济增长的作用机制,因此应该积极改善能源消费结构,以能源消费结构升级引导经济增长方式的转变,减少高能耗、低收益的落后产能,促进经济实现高质量发展。
第三,减少经济增长的能源消耗。 常州市滞后1 期的经济增长一定程度上提高了当期能源消费量,说明常州市经济发展还未完全实现产业结构升级,经济增长仍然一定程度上依赖于能源消费。 因此,应该继续推进产业结构的转型升级,促进经济增长方式向创新驱动转变。 同时,明确将自主创新作为核心推动力,通过建设现代化产业体系和加快产业转型升级,实现常州市向服务经济为主体、现代服务业和先进制造业、高新技术产业融合发展的工业化后期阶段转型。
