基于SSI-MSVM的调相机轴承故障诊断方法*

2021-04-23张玉良马宏忠蒋梦瑶林元棣

电机与控制应用 2021年3期

张玉良, 马宏忠, 蒋梦瑶, 蔚超, 林元棣

(1.河海大学能源与电气学院,江苏南京 211100；2.国网江苏省电力有限公司电力科学研究院,江苏南京 211103)

0 引言

随着新能源的并网与特高压直流输电的发展，电网对无功调节的要求也逐步提高。调相机是一种大型无功调节设备，其发出无功和吸收无功的能力均较强，在电力系统中可以加强电压的动态调节能力[1-2]。例如在特高压变电站，调相机可以有效抑制电力系统电压变化，尤其在电网侧可以快速吸收由于换相失败而产生的无功功率，同时可以大量提供无功功率，加快故障后系统电压的恢复。因此，大型调相机是电力系统中调节无功的重要装置，保证调相机的安全稳定运行具有重大意义。轴承是调相机组重要的组成部分之一，一旦故障可能导致机组停机且维护成本较高[3-4]。因此，开发一种准确的调相机轴承故障诊断方法，对提高调相机组的安全性和经济性具有重要的作用。

对于调相机等旋转机械，振动分析法是一种有效的状态监测方法[5]。根据相关文献，已有大量针对振动信号的方法用于各种旋转机械的转轴及轴承故障检测，例如小波变换、频谱分析、经验模态分解等。与其他方法相比，经验模态分解在振动信号的处理中有着较好的效果，但其耗时过长。经验小波变换和变分模态分解具有更强的信号处理能力，可以避免模态混叠，并具有较强的鲁棒性。随机子空间识别法(SSI)具有更高的辨识精度和抗干扰能力，可以从复杂的环境激励中提取特征信息。SSI直接建立了一个基于时域数据的模型，可以识别模式参数，这种结构适用于挖掘故障的基本信息[6]。

近年来，人工智能故障诊断方法在调相机故障诊断中得到了广泛的应用。支持向量机(SVM)作为一种智能故障诊断方法，在小样本、非线性、高维模式识别等问题上具有较大的优势[7]。文献[8]针对轴承的不同状态，应用SVM进行分类计算，并利用相关的试验证明了该方法的有效性。文献[9]设计了一种将局部线性嵌入算法与小波包相结合的故障特征提取法，然后利用SVM对轴承的故障程度进行分类识别。文献[10]提出了一种经验模态分解和SVM相结合的故障诊断方法，对不同的轴承故障状态进行识别诊断。然而传统的SVM在解决数据分类问题时仅仅使用了单一的核函数，难以适用于复杂的分类问题，特别是对异构以及不均衡的数据分类。为了增加SVM对复杂数据的处理能力，基于文献[11-12]，本文采用多核支持向量机(MSVM)对调相机轴承进行故障诊断。MSVM不仅具有单核SVM的泛化能力，还具有一定的自学习能力，适应性和鲁棒性均较好[13]。

综上，本文提出了一种基于SSI-MSVM的调相机轴承故障诊断方法。通过SSI对采集到的调相机轴承振动信号预处理，采用正交投影和奇异值分解得到状态矩阵。再利用参数估计获取系统矩阵及特征值。然后，对MSVM进行有监督的训练，实现对调相机轴承故障的识别诊断。

1 调相机轴承故障机理

在正常运行过程中，如果调相机轴承振动超过允许范围，很大程度上会导致其轴承、轴颈、密封瓦等部件磨损，甚至出现定子的膛内进油等严重故障[14-15]，影响系统的安全运行。因此，调相机的轴承振动值应该维持在一定的标准范围内。

导致调相机轴承振动的原因有：

(1) 调相机组转子质量不平衡，在高速旋转时转子上的离心力可能过大，在轴承上产生激振力，导致轴承出现异常振动。

(2) 调相机组轴系中心差导致轴振过大，引发机组轴承振动。

(3) 调相机定子载荷分配不均引发机组在正常运行中振动过大。

(4) 机组冷却系统故障导致调相机部分出现不均膨胀，引发机组轴承振动。

以上列举了4种常见可能导致调相机轴承振动的原因，本文的故障试验是基于机组载荷分配不均进行的，因此主要分析调相机定子载荷分配不均造成的振动问题。

调相机轴承通常置于其定子两端的端盖上，端盖与调相机定子相固定，定子底座通常是利用垫铁安装在台板上。调相机在自身重力的作用下将定子底座固定在基础台板上，但为了提高机组的刚度，需要根据调相机定子底座的重力挠曲线对垫铁进行调整，垫铁的调整则需要依据调相机定子的载荷分配试验。若调相机载荷分配不均，则定子可能不平衡，其两侧的振动值也会出现较大差距，使机组整体的刚度降低，影响到调相机转子轴承的支撑系统，使其轴承座上出现大幅振动。

调相机组轴承座的振动主要源于轴系激振力和系统支撑动刚度2个方面，二者关系可以表示为

(1)

式中：A为振动的幅值；α为系数;F为激振力；Kd为系统支撑动刚度。

由式(1)可以看出，调相机轴承的振动幅值正比于激振力，反比于系统的支撑动刚度，因此激振力越大，支撑动刚度越小，轴承座上产生的振动则越大。

2 随机子空间识别

2.1 随机状态空间模型

SSI是一种利用采集到的数据建立线性状态空间模型的黑盒识别方法[16-19]，对于提取振动信号的特征非常适用，其随机状态空间模型如下：

(2)

式中：Xk∈Rn、Yk∈Rl分别为在离散时间k下的系统状态变量和输出；A∈Rn×n是对系统动态行为进行描述的系统矩阵；wk∈Rn、vk∈Rl分别是系统和测量噪声;C∈Rl×n是系统输出矩阵。

2.2 SSI应用

SSI过程一般分为3个步骤：正交投影、奇异值分解、系统参数估计。

2.2.1 正交投影

对由测量信号构成的Hankel矩阵进行定义：

(3)

式中：yk表示采集信号,k=1,2,…,i+j+N;Yp表示矩阵Y的过去部分，其行数为i;Yf表示矩阵Y的未来部分，其行数为j+1，i、j一般情况下不小于模型矩阵的最大阶数，即min{i,j+1}≥n，而Hankel矩阵的列数N一般情况下远大于i和j+1，即N≫max{i,j+1}。

将矩阵Y重新划分如下：

(4)

再由式(5)将Yf正交投影到Yp空间：

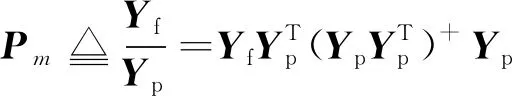
(5)

式中：Pm表示投影矩阵；(·)+表示穆尔-彭罗斯广义逆矩阵。

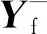
(6)

2.2.2 奇异值分解

利用奇异值分解法对投影矩阵Pm进行如下分析：

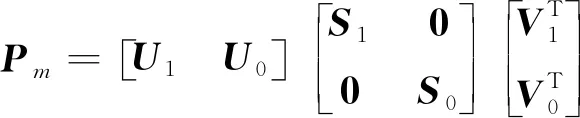
(7)

式中:U1、V1是酉矩阵，S1=diag{σ1,σ2,…,σi,…,σn}是对角矩阵，σi是S1的第i个奇异值;U0、V0、S0是零矩阵。

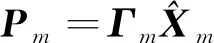
(8)

同样，反馈矩阵Pm-1可以表示为

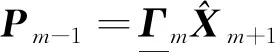
(9)

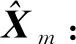
(10)

(11)

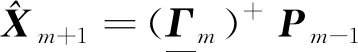
(12)

2.2.3 系统参数估计

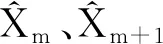
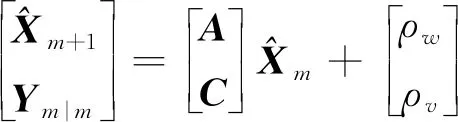
(13)

对系统矩阵A和输出矩阵C进行最小二乘法估计可得：

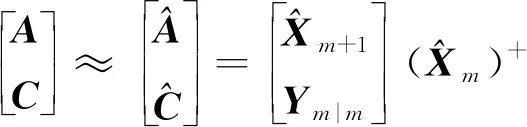
(14)

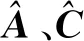
式(14)中，系统矩阵A包含了由振动数据构成的系统模型特征信息，即系统矩阵A的特征值对应于不同的故障模式。

矩阵A的特征值可分解为

A=UΣVT

(15)

式中：U为系统矩阵A中的左奇异矩阵;VT为系统矩阵A中的右奇异矩阵的转置;Σ=diag{λ1,λ1,…,λi,…,λn}为对角矩阵，λi为系统矩阵A中的第i个奇异值。

3 标准SVM和MSVM

传统调相机轴承故障诊断方法是使用单一核函数的标准SVM，进行相关的模型训练与学习分类。但轴承数据的复杂性和参数之间类似非线性的内部关系使标准SVM难以达到较好的分类效果。相比之下,MSVM则具有较强的通用性，且在计算过程中效率更高，可以同时兼具性能和全局特性。

3.1 标准SVM

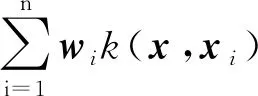
(16)

式中:ei为松弛变量e的第i个元素，i=1,2,…,n；C为惩罚系数；b为原点至超平面的距离；φ(·)为映射函数。

将约束优化问题通过拉格朗日乘子αi变换成对偶优化问题，则最终的分类决策函数为

f(x)=sgn[∑yiαik(x,xi)+b]

(17)

3.2 MSVM

在故障诊断过程中的关键点为SVM的核函数，不同的核函数对应不同的判别函数，直接影响到SVM的诊断精度。SVM的核函数主要分为局部核函数和全局核函数。

高斯核函数是一种典型的局部核函数，描述如下：

(18)

式中:σ为核函数。

多项式核函数则是一种典型的全局核函数，描述如下：

(19)

式中：d为核函数。

传统SVM仅使用单一的核函数，可以较为方便地解决简单的数据分类问题，但针对调相机的轴承故障诊断等复杂问题存在一定的局限性。为了提高传统SVM的性能，提出一种将局部核函数和全局核函数相结合的方法来构建MSVM，描述如下：

Kmin(xi,xj)=λKRBF(xi,xj)+(1-λ)Kploy(xi,xj)

(20)

式中:λ为调优参数，0≤λ≤1。

根据式(20)可以发现，在λ=0时多核函数变为高斯核函数，在λ=1时多核函数变为多项式核函数。多核函数通过调整调优参数λ来适应不同的输入样本，因此MSVM在应用的过程中具有一定的学习和泛化能力。

4 基于SSI-MSVM的故障诊断模型

本文所提的基于SSI-MSVM的调相机轴承故障诊断方法的整体诊断流程如图1所示。

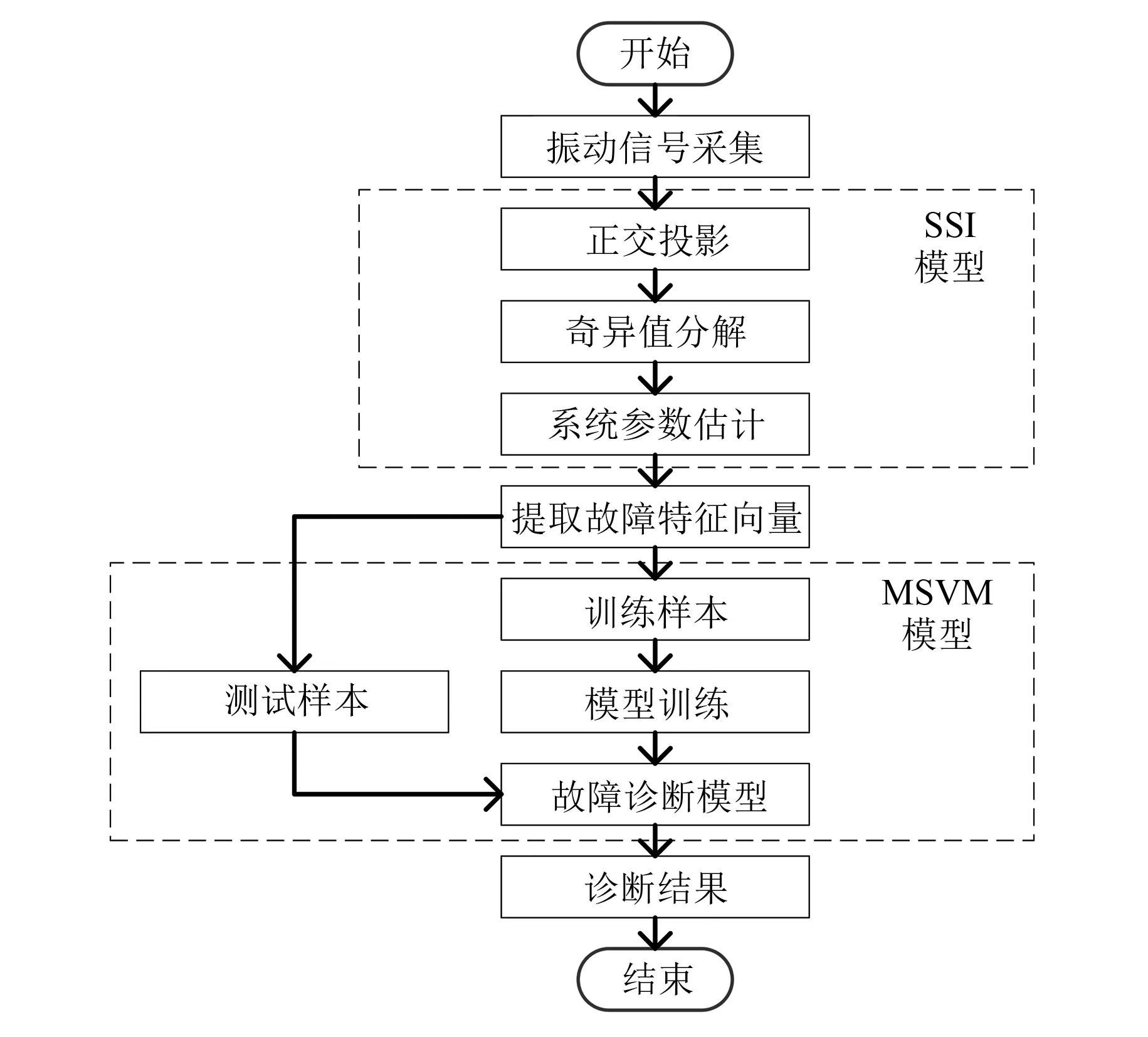
图1 基于SSI-MSVM的调相机轴承故障诊断流程图

具体流程如下：

(1) 通过在调相机轴承表面不同位置设置的振动传感器采集调相机轴承的振动信号。

(2) 先将采集到的调相机轴承振动信号建立随机状态空间模型，然后利用奇异值分解对系统矩阵A进行参数估计，提取特征值作为故障特征向量。

(3) 以不同故障样本数据对MSVM进行模型训练，构建故障诊断模型。训练完成的调相机故障诊断模型可以对不同的模式进行识别。

(4) 最后将用于测试的样本输入完成训练的模型中进行故障诊断，根据MSVM模型的输出可以确定调相机轴承的工作状态和故障类型。

5 试验结果与分析

为了验证基于SSI-MSVM故障诊断方法的实用性和有效性，对某特高压变电站一台调相机开展轴承故障诊断试验。试验过程中将8个加速度振动传感器分别置于调相机轴承及机座外壳表面用以获取振动数据。

试验中，加速度振动传感器通过磁性底座吸附在各个测点，通过MPS-140801数据采集卡采集振动数据，采集频率为8 000 Hz，有效分辨率21.8 bit，信噪比121 dB。试验现场如图2所示。测点布置情况如图3所示。

图2 试验现场

图3 轴承座外部截面测点布置情况

为了模拟调相机轴承故障，选取了调相机载荷不均匀时的振动数据。由于故障时右侧载荷偏轻，因此选取了7号测点的数据进行分析。调相机轴承在正常运行和弱、强故障模式下的部分振动信号与局部放大图如图4、图5所示。图4、图5中，2组故障信号分别采集自载荷分配存在偏差时处于3 000 r/min和1 500 r/min下的调相机轴承，分别模拟了调相机轴承的强故障和弱故障模式。与正常运行时的振动信号波形相比，强故障模式下存在断层、不规则且振幅较大的冲击信号，而弱故障模式下则冲击信号较少。

图4 调相机轴承在正常运行和弱、强故障模式下的部分振动信号

图5 调相机轴承在正常运行和弱、强故障模式下的部分振动信号局部放大图

在SSI识别的过程中，每个样本的数据点数量应足以保证故障特征提取的有效性，因此将每10 000个调相机轴承振动信号的数据点作为一组样本，且Hankel矩阵Yf和Yp均为10×9 990维矩阵。通过SSI对采集到的调相机轴承振动信号进行分析，将投影矩阵进行奇异值分解，并得到系统矩阵的特征值。图6为SSI模型提取到的不同工况下调相机轴承振动信号的特征。图6中，0～0.25是振动信号经SSI分析得到的特征值标量。

由图6可以发现，所有的特征值均分布在正多边形的附近，结果表明该SSI模型是有效的。同时，对于不同模拟故障下的振动数据特征值，其分布位置不同，表明聚类算法可以用来区分这些不同的特征值。

图6 调相机轴承在不同工况下利用SSI提取的特征

试验中发现，当训练样本量达到160组时模型的诊断结果已趋于稳定，因此为了进一步提高精度，对于调相机轴承在正常运行和强、弱故障模式，各提取200组有标记数据作为训练样本，训练基于SSI和MSVM、K-means聚类、模糊均值聚类(FCM)、标准SVM的故障诊断模型。并额外提取3种工况下每种30组数据，共计90组未标记数据作为测试样本，用于检验各个模型的诊断精度。对额外提取的90组数据利用MSVM进行诊断得到的结果如表1所示。

表1 SSI-MSVM对测试样本诊断结果

同样将测试样本送入其余3种模型进行诊断作对比分析，不同模型的诊断结果及精度如表2所示。图7展示了基于SSI的MSVM与其他方法对比试验的可视化结果。

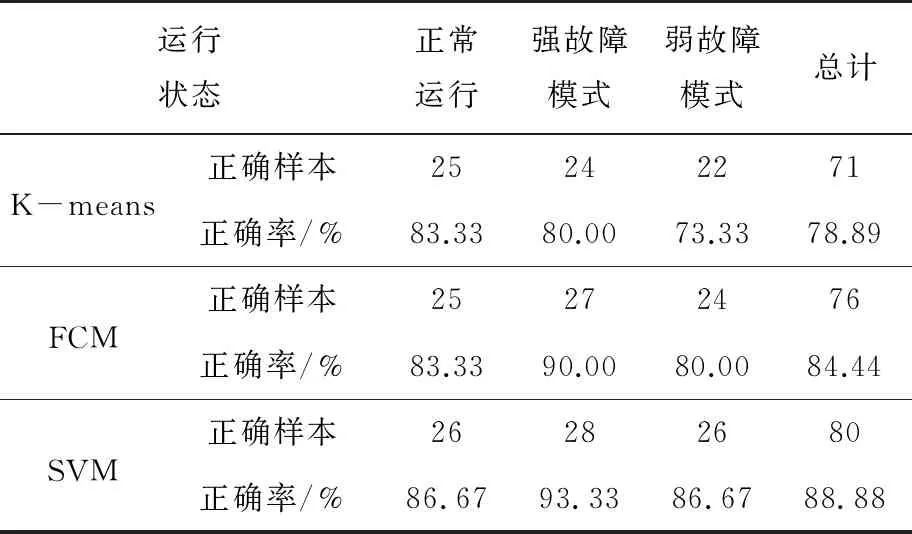
表2 K-means、FCM、SVM模型故障诊断结果准确率对比

图7 不同诊断模型的诊断精度对比

由图7可以看出，基于SSI-MSVM的故障诊断准确率为93.33%，而K-means聚类、FCM、标准SVM的故障诊断准确率分别为78.89%、84.44%、88.88%。在对没有标记的故障数据进行诊断时，多核函数可以调整调优参数来优化分类结果。在实际试验计算过程中发现，由高斯核函数和多项式核函数组合成的MSVM能够获得较好的分类性能和适应性，且优于单一核函数的标准SVM。

综上所述，基于SSI-MSVM的方法诊断准确率高于K-means聚类、FCM、标准SVM，由此证明本文提出的诊断模型优于传统诊断方法。