基于改进最小二乘法永磁同步电机多参量辨识*

宋建国, 张振路, 李向诚

(北京工业大学 信息学部，北京 100124)

0 引 言

由于温升、磁路饱和负载扰动等因素，永磁同步电机(PMSM)在实际运行过程中往往会出现电磁参数不匹配的情况，导致控制效果不佳甚至电机故障。因此，实时精确获取电机参数可以有效保障电机高性能的安全运行[1-2]。

PMSM参数在线辨识的难点主要集中在多参数同时辨识上，由于电机数学模型方程数小于待辨识参量数，其结果的收敛性和唯一性会因电机工况变化而缺乏理论支撑。为此，国内外研究提出了诸多解决办法。文献[3-4]通过注入扰动信号增加方程的秩从而建立满秩方程组。文献[5-6]通过测量额外的电气参量，构建其他的方程纳入到辨识模型中。

根据电机的运行状态可以构建电机的动态数学模型和稳态数学模型。动态数学模型基于PMSM的动态电压方程，需要采集足够多不同状态时的辨识数据，但因为微分器引入的高频分量需要滤波处理，所以难以保证辨识数据输入辨识算法的时效性[7]。电机稳定运行时，稳态数学模型基于PMSM的稳态电压方程建立，方程中不含电流微分项，数据集相位延迟导致的错拍输入问题得以解决[8-9]。因此，本文构建稳态数学模型，利用遗忘因子递推最小二乘法分步迭代辨识，无需外部信号注入，解决了PMSM同时辨识多个参数的问题。

1 数学模型及系统结构

1.1 PMSM的稳态数学模型

在实际的PMSM控制应用中，PMSM是一个多变量、强耦合的非线性系统。为了便于研究，先假定PMSM三相对称平衡，反电动势为正弦波形，忽略磁滞和涡流损耗的影响，忽略谐波因素等[10-11]。从而得到PMSM在旋转坐标系下dq轴的动态电压方程：

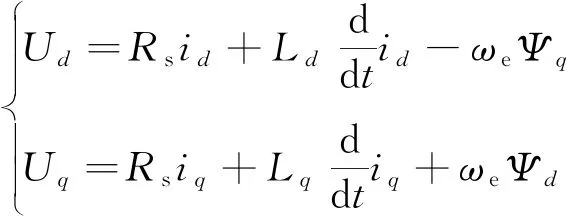
(1)

式中：Ud、Uq为d、q轴电压；Rs为定子电阻；id、iq为d、q轴电流；Ld、Lq为d、q轴电感；ωe为转子电角速度；Ψd、Ψq为d、q轴磁链，Ψd=Ldid+Ψf，Ψq=Lqiq。

整理式(1)可得：

(2)

式中：Ψf为转子磁链。

对于表贴式永磁同步电机(SPMSM),d、q轴电相感等，即Ld=Lq=Ls,则有:

(3)

电机平稳运行时，动态电压方程的电流微分部分为零，可得SPMSM稳态电压方程：

(4)

1.2 控制系统在线辨识框图

PMSM参数在线辨识需要在电机运行过程中实时采集数据并送至DSP运算得到参数结果。控制结构采用id=0控制方式，在电机平稳运行的工况下采集旋转坐标系下的电压电流信息和转速信息,通过在线辨识算法得到电机参数。系统总体框图如图1所示。

图1 系统总体框图

2 遗忘因子递推最小二乘法

本文辨识算法基于最小二乘法在线辨识PMSM电气参数：定子电阻Rs、转子磁链Ψf和dq轴电感Ls。模型的最小二乘法如下：

Ym=ΦmΘ

(5)

考虑到DSP运算能力和大数据量的矛盾，推导适合离散系统运算且计算量合适的递推最小二乘法，同时为了解决“数据饱和”引起的收敛误差问题，引入遗忘因子调节新旧数据的比例，利用新引入的数据进行递推计算，直到参数估计收敛到正确结果[12]。遗忘因子递推最小二乘法的表达式如下：

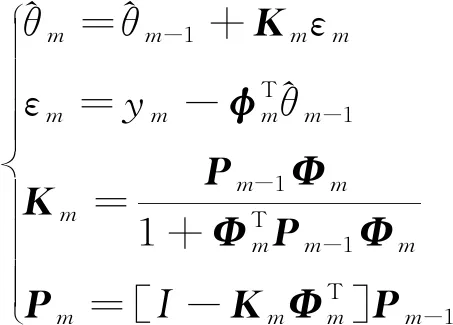
(6)

3 改进递推最小二乘算法

本文基于SPMSM进行参数辨识研究，q轴电感和d轴电感相等，故只需要辨识Rs、Ψf和Ls3个参数，但仍不能满足数学模型满秩要求。

通过对3个参数的分析可知，与电流的瞬时变化相比，Rs和Ψf的变化缓慢，可以在短时间内视为常量。而电感Ls变化较快且受影响的因素多，甚至会因转子角度不同而产生较大差异。因此，将定子电阻Rs和转子磁链Ψf划分为慢变化参量，分时分步固定为常量满足系统的满秩条件；将电感Ls划分为快变化参量，在慢参量固定的时间内进行快参量辨识，实现对快参量变化的跟踪。

3.1 慢参量辨识

慢参量辨识算法分为两步循环迭代辨识，在已知一个慢参量Rs或Ψf的情况下，辨识另一个慢参量和快参量，在2个慢参量逐步收敛稳定到小于误差要求后，固定慢参量的值，为快参量辨识算法提供参数。因为电阻Rs可以通过毫欧表或直流伏安法测量获得，方便简单，所以本文在慢参量辨识过程中将Rs固定为入口参数。

在定子电阻Rs初次测量固定或辨识固定的情况下，辨识转子磁链Ψf和电感Ls。将稳态电压方程式(4)变换得到式(7)：

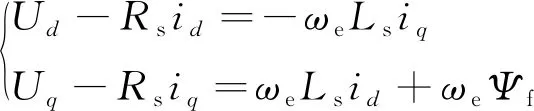
(7)

结合式(5)和式(6)，令n=2,可得输入数据、输出数据以及待辨识的参数序列如下：

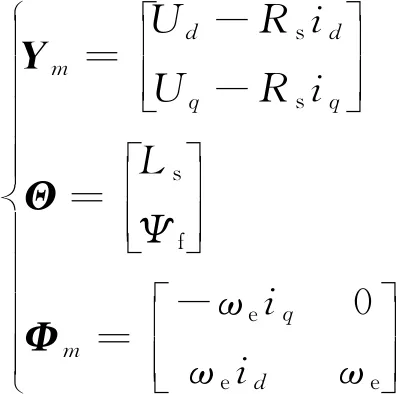
(8)

在转子磁链Ψf辨识固定的情况下，辨识定子电阻Rs和电感Ls。将稳态电压方程式(4)变换可得：

(9)

结合式(5)和式(6)，令n=2,可得输入数据、输出数据以及待辨识的参数序列如下：

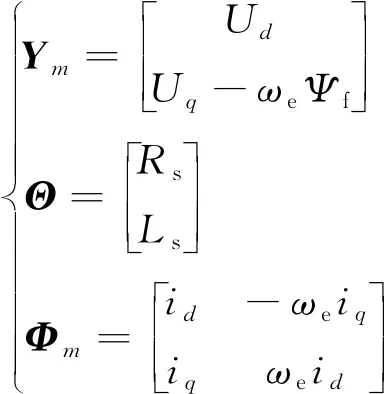
(10)

3.2 快参量辨识

慢参量辨识算法迭代运算得到收敛的Rs和Ψf，在设定的时间内固定慢参量的值并进入快参量辨识算法，辨识跟踪电感Ls。由于该部分待辨识参数只有一个，则基于q轴稳态电压方程合理构造辨识模型。将稳态电压方程式(4)变换得到：

Uq-Rsiq-ωeΨf=ωeLsid

(11)

结合式(5)和式(6)，令n=1,可得输入数据、输出数据以及待辨识的参数序列如下：

(12)

慢辨识算法中为了增加算法稳定性和促成最小二乘法格式，待辨识参数序列也引入了Ls。但慢辨识算法主要关注慢参量的收敛，而后续试验也发现在Rs和Ψf收敛时，慢参量辨识算法辨识的Ls误差较大。因此，电感Ls的辨识采用快辨识算法。

3.3 快慢参量分步迭代辨识

辨识算法流程如图2所示。将参数辨识算法分为慢辨识与快辨识2部分，在电机稳定运行的阶段进入中断，读取电压电流和转速信号。初次辨识需要先测定慢参数类型中的一个，其中定子电阻Rs可以利用仪器直接测得，转子磁链可以在空载拖动指定转速的情况下，给定dq轴电流为零测得。若不是初次辨识，判断慢参量是否收敛，如果不收敛，进入慢参量辨识阶段；如果收敛，在设定的时间或变化范围内认定慢参量不改变，进入快参量辨识阶段。直到设定的时间达到或者变化的范围超出，认定慢参量发生改变，进入慢参量辨识算法再次更新慢参量的值。

图2 辨识算法程序流程图

4 试验结果

试验平台搭建如图3所示。控制器采用TI公司的TMS320F28335浮点型DSP,进行电机矢量控制算法及参数辨识算法的开发。

图3 试验平台

电机型号为90ST-M02430，SPMSM参数如表1所示。

表1 SPMSM参数

采用id=0控制方式，设计PMSM矢量控制算法以及双闭环调节使电机稳定运行。通过电流传感器采集相电流，经过AD转换送至DSP控制算法所需，观察电机起动和平稳运行阶段的相电流波形，分析得到辨识算法需要的电机稳态运行时的可靠数据集。图4为电机空载起动后平稳运行时的两相相电流波形。可以看出，电流波形平滑，无尖峰电流，辨识数据满足稳态电压方程。

图4 电机稳态运行相电流波形

4.1 空载起动辨识试验

基于以上试验平台，采用图2的分步迭代辨识算法，即改进遗忘因子递推最小二乘算法(FRLS)进行参数辨识。利用毫欧表测得实际电机参数Rs,辨识算法进入慢参量辨识阶段，当Ψf的值收敛且变化率小于5%时，固定Ψf的值。Ψf辨识结果如图5所示。

图5 空载试验Ψf辨识结果

由图5可以看出，在约0.4 s时Ψf已经基本收敛稳定，相较于改进前的遗忘因子FRLS，收敛速度较快。当Rs和Ψf均固定时进入快参量辨识阶段。由于慢参量会缓慢变化，需要阶段更新，Rs辨识结果如图6所示。

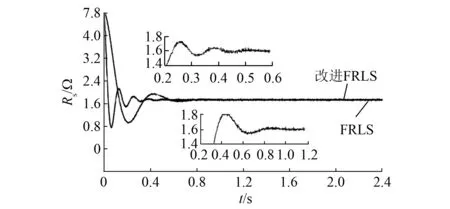
图6 空载试验Rs辨识结果

由图6可以看出，改进FRLS算法在0.5 s时Rs已经基本收敛稳定，与FRLS算法相比，辨识速度较快。因为在此之前慢参量Rs和Ψf均没有收敛，所以0.5 s之前FRLS和改进FRLS的Ls辨识结果均不稳定且偏离了真实值。0.5 s之后改进FRLS进入快辨识阶段，慢参量已经收敛且代入快辨识算法，Ls很快收敛到了准确值。而FRLS由于仍然欠秩，Ls辨识结果偏离了真实值。Ls辨识结果如图7所示。

图7 空载试验Ls辨识结果

4.2 负载辨识试验

电机负载运行所伴随的温度变化和磁路饱和现象是引起电磁参数变化的重要因素。定子电阻会随着温度的升高呈现明显的非线性变化。铁磁材料的磁导率会随温度不同和磁路饱和现象出现非线性变化，进而影响电感和转子磁链的变化。不同负载工况下的永磁体磁链如图8所示。

图8 不同负载工况下永磁体磁链

电机空载起动运行至稳定阶段后，进行负载工况下辨识试验。初始给定空载运行，持续至5 s时通过测功机平台给定额定负载，通过分步迭代辨识算法对试验电机的定子电阻Rs、电感Ls及磁链Ψf进行相应辨识。

负载试验定子电阻Rs辨识结果如图9所示。可以看出，在5 s前为空载运行辨识结果，辨识值稳定在真实值；在5 s给定额定负载后，定子电流增大导致绕组温度升高，Rs辨识值略有增大。

图9 负载试验Rs辨识结果

负载试验电感Ls辨识结果如图10所示。给定额定负载前的辨识结果基本接近于真实值，在5 s给定额定负载后，定子电流增大导致定子电感磁化曲线靠拢饱和区域，Ls辨识值相应减小。

图10 负载试验Ls辨识结果

负载试验磁链Ψf试验辨识结果如图11所示。空载工况下辨识结果与真实值基本一致，在5 s给定额定负载，Ψf辨识值相应增大，辨识结果抖振略有增大。

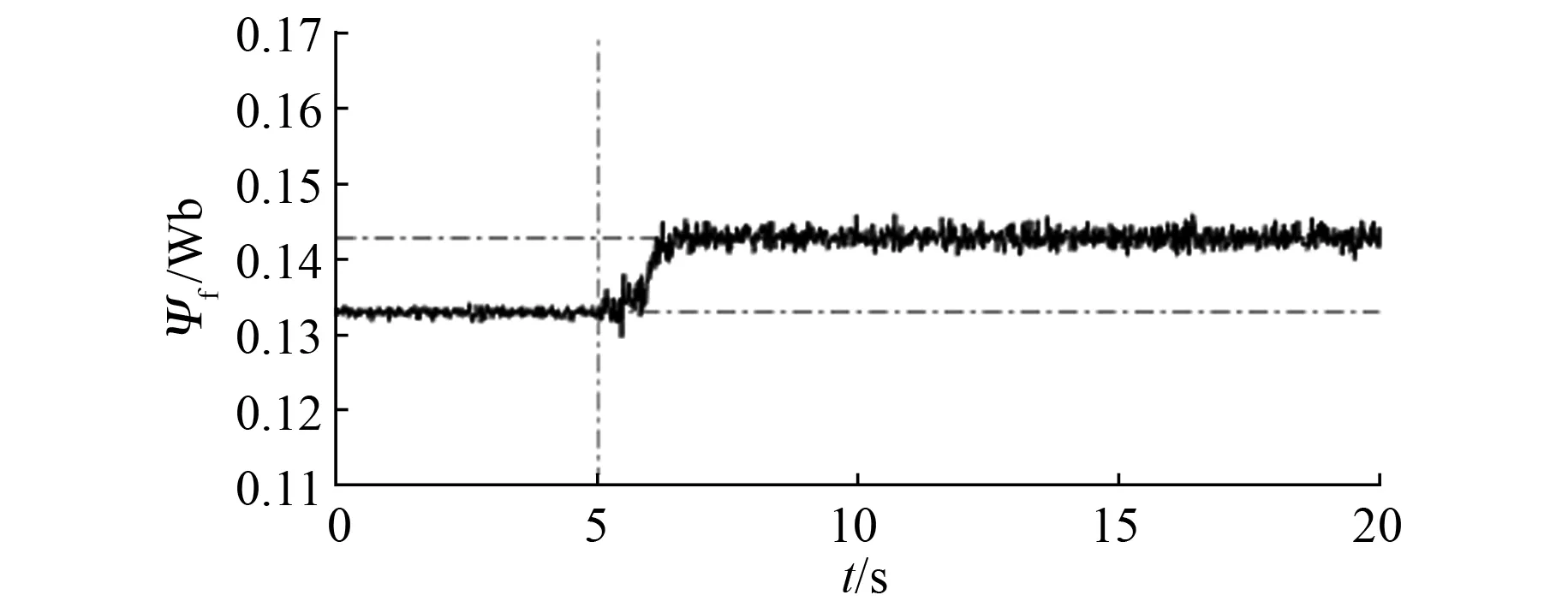
图11 负载试验Ψf辨识结果

4.3 温升动态辨识试验

电机参数变化受温度的影响较大，但是电机内部的温度难以直接测量。由焦耳定律可知，通电导体差生的热量跟电流的二次方和时间成正比，跟导体电阻成反比。故考虑控制电机稳态运行时间，以电机定子电流标定电机内部温度。

设计测功机平台对拖试验将电机拖到期望转速，通过上位机控制电机以不同的定子电流稳态运行相同时间(设定15 min)，进而改变不同温度下的电阻和磁链。利用离线辨识和分步辨识算法辨识电机参数，结果如图12所示。

图12 慢参数随温度变化曲线

由图12可以看出，随着温度上升，Rs会缓慢上升，Ψf会缓慢下降，而快慢参量分步迭代辨识算法可以准确地跟踪参数的变化。

5 结 语

本文分析了PMSM参数动态辨识的数据相位延迟错拍和稳态辨识模型欠秩问题。在矢量控制的基础上控制电机平稳运行，采集稳态数据。设计以参量变化快慢为依据的分步迭代辨识算法，通过FRLS辨识电机参数，能够快速收敛至实际值，并且随着温度的改变可以有效地跟随电机参数的变化。而且分步辨识算法可以根据实际运行情况分阶段调节计算量，降低了DSP的计算压力。