液压增速传动风力发电恒频控制研究
2021-04-23石青易邓晓刚岳凯凯肖鑫源
石青易, 邓晓刚, 岳凯凯, 肖鑫源, 张 硕
(重庆科技学院 机械与动力工程学院, 重庆 401331)
引言
当今,风力发电机组正逐渐朝着大型化发展,传统齿轮箱式和直驱式风力发电机组易故障[1]、安装与维护的高成本问题愈发明显。液压型风力发电机组由于具有系统刚度大和易于实现无级调速等优势而逐渐引起人们的关注[2]。
风力发电机组恒频发电的关键问题在于变量马达的稳速控制, 国内外学者对此进行了相关研究。VAEZI M等[3]研究了在风速载荷变化的条件下,液压型风力发电机组恒转速输出控制问题。石茂顺等[4]采用液压变压器原理对发电机输出转速进行控制,通过液压变压器的调压原理,实现发电机的稳速控制;艾超等[5-6]提出了基于动态面控制的稳速输出控制等多种恒转速输出控制方法,但其模拟实验与实际风场有较大差别。李富柱等[7]针对一种双调节液压变速恒频控制展开了研究,但与蓄能器直接安装在高压管路的方式相比蓄能效率降低。林勇刚等[8]提出了一种机液混合传动的液压型风力发电机组,并验证了该机型的转速控制,但不能消除齿轮传动故障率高的缺点。WEI L等[9-10]针对600 kW风力发电机组采用液压蓄能的方式对机组转速进行控制。
在液压型风力发电机组中,恒频控制主要受风力机输入的波动性以及负载扰动等因素的影响。因此,针对低速定量泵-高速变量马达增速传动闭式回路系统,在恒流源控制基础上,采用PID控制器[11]补偿斜盘摆角方法[12],并对其主传动控制系统进行仿真和实验分析,达到恒频控制的目的。
1 液压风力发电机组
图1为工作原理简图,其结构由风力机模拟系统、低速大扭矩定量泵[13]、变量马达、电励磁同步发电机和补油设备等几部分组成。该系统用变频电机模拟风力机在低风速下转动,带动定量泵输出高压油。在安全阀不作用的情况下,液压油通过高压管路流入马达内部,驱动其内部轴旋转工作。变量马达轴端与同步发电机内部转子直接连接,在高速旋转作用下产生电能。

图1 工作原理简图
由同步发电机并网条件可知[12],我国电网频率为50 Hz,考虑产生的电能质量,要求同步发电机的转速频率与电网频率一致,其偏差不超过±0.2 Hz (0.4%),故需要控制发电机转速稳定在(1500±6) r/min。由于系统为闭环控制系统,在安全阀不作用情况下,定量泵输出流量全部流经变量马达,即系统处于恒流源状态。因此,要想保持变量马达转速不变,需要控制变量马达斜盘摆角随着定量泵转速变化。利用定量泵轴上的转速传感器测量出定量泵转速,然后折算出变量马达摆角基准值,该值可通过斜盘摆角控制器调节变量马达排量,使变量马达转速到达1500 r/min附近。但由于风速变化等干扰因素,变量马达转速会存在波动,难以稳定。由于PID 控制器具有方便性、鲁棒性好等特点,能够稳定控制在某一给定值上,故测量变量马达输出转速,与给定的1500 r/min形成偏差值,通过PID控制器(斜盘摆角补偿控制器)输出斜盘摆角补偿值,补偿斜盘摆角基准实现恒转速输出控制。
2 机组数学建模
定量泵输出流量Qp为:
Qp=Dpωp-Ctpph1
(1)
式中,Dp—— 低速泵的额定排量,m3/rad
ωp—— 低速泵的输入转速,rad/s
Ctp—— 低速泵的泄漏系数,m3/(s·Pa)
ph1—— 泵的进出口压差,Pa
定量泵负载力矩Tp为:
Tp=Qpph1/ηp
(2)
式中,ηp为定量泵机械效率。
定量泵的力矩平衡方程:
(3)
式中,Tt—— 风力机输出转矩,N·m
θp—— 定量泵转角,rad
Jp—— 定量泵轴上的转动惯量,kg·m2
Bp—— 定量泵的阻尼系数,m·s/rad
Gp—— 定量泵端的负载弹簧刚度,N/m
变量马达排量Dm为:
Dm=Kmγ
(4)
式中,Km—— 变量马达排量梯度,m3/rad
γ—— 变量马达摆角位置,(°)
变量马达流量Qm为:
Qm=Kmγωm+Ctmph2
(5)
式中,ωm—— 为变量马达转速,rad/min
Ctm—— 变量马达泄漏系数,m3/(s·Pa)
ph2—— 泵的进出口压差,Pa
变量马达输出转矩Tm为:
Tm=Qmph2/ηm
(6)
式中,ηm为变量马达机械效率。
变量马达的力矩平衡方程:
(7)
式中,Te—— 变量马达轴上的转矩,N·m
θm—— 变量马达转角,rad
Jm—— 变量马达轴上的转动惯量,kg·m2
Bm—— 变量马达的阻尼系数,m·s/rad
Gm—— 变量马达端的负载弹簧刚度,N/m
高压管路流量方程为:
(8)
式中,V0—— 主传动控制系统的高压腔内总容积,m3
βe—— 高压油的综合体积弹性模量,Pa
ph—— 高压管路压力,Pa
3 恒频控制仿真与实验研究
以37 kW液压型风力发电机组实验平台(如图2所示)为基础,探究变量马达稳速输出的影响因素以及恒转速输出的抗干扰性能。
仿真利用AMESim软件[14]建立液压型风力发电机组定量泵-变量马达主传动控制系统模型,通过改变电动机输入转速模拟不同风速,改变负载溢流阀压力模拟负载变化。实验利用变频电机通过减速箱带动低速定量泵转动[15](模拟低风速输入),然后通过主传动控制系统驱使变量马达高速转动,带动与其直接连接的电励磁同步发电机产生频率稳定的电能。
液压系统主要结构基本参数见表1。

1.变量马达 2.变频电机 3.电控柜 4.补油泵 5.定量泵 6.同步发电机图2 37 kW试验平台
3.1 变量马达转速影响因素分析
采用恒转速控制方法,分别研究马达斜盘摆角折算系数和不同低速泵转速输入对高速变量马达恒定输出转速的影响。
1) 不同摆角折算系数对高速变量马达恒定输出转速的影响分析
仿真和试验时,低速泵转速输入和高速变量马达速度控制闭环PID参数保持不变。给定马达斜盘摆角基准折算系数分别为0.0788,0.0807,0.0826,低速泵转速输入如图3所示,分析液压型风力发电机组变量马达转速变化,如图4所示。
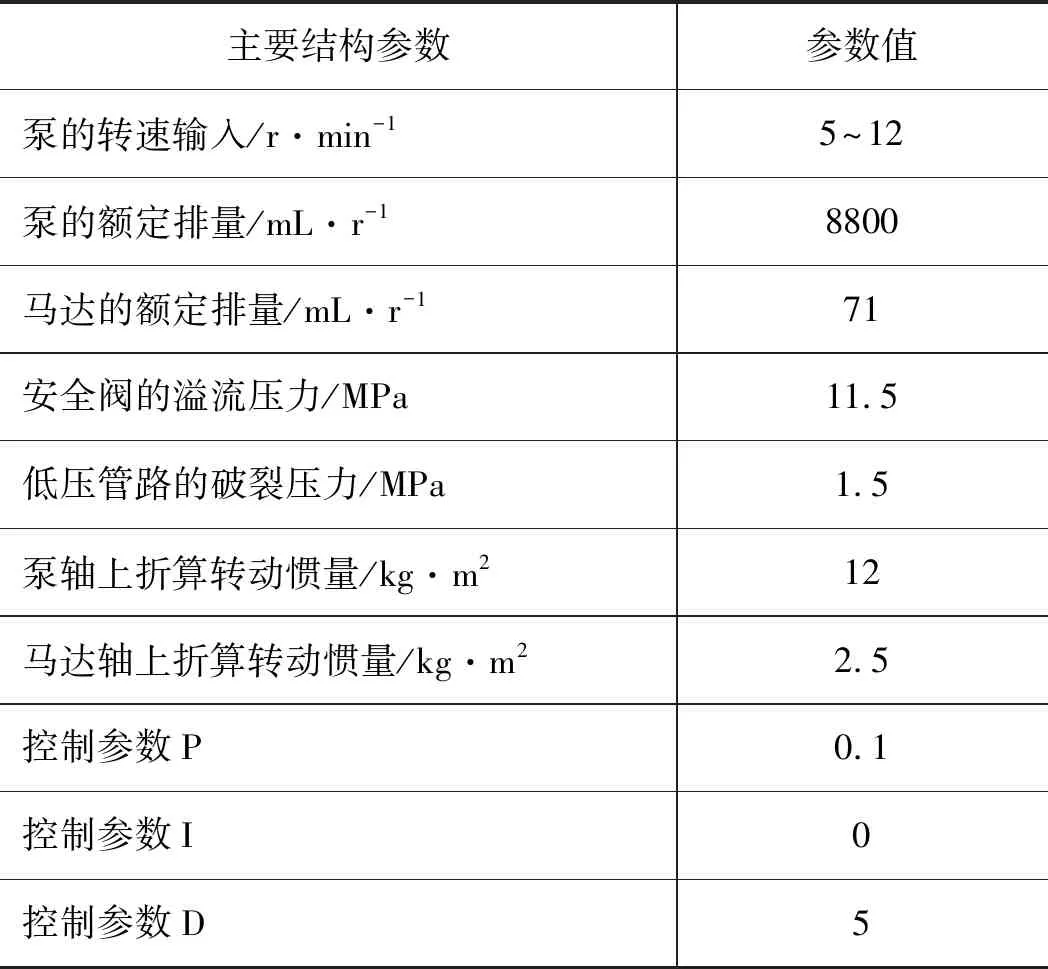
表1 基本参数

图3 不同折算系数时低速泵转速输入曲线
由仿真和试验曲线可知,马达斜盘摆角折算系数在0.0788~0.0826小范围变化时,变量马达输出转速数值基本一致,在(1500±2)r/min内波动,没有产生明显变化,同时满足(1500±6)r/min的转速控制要求。可见该系数对变量马达恒转速输出的影响不明显。

图4 不同折算系数时变量马达输出转速曲线
2) 不同低速泵转速输入对高速变量马达恒定输出转速的影响分析
仿真和试验时,高速变量马达斜盘摆角基准折算系数和其速度控制闭环PID参数保持不变。给定不同低速泵转速7,8,9 r/min,如图5所示。分析液压型风力发电机组变量马达转速变化,如图6所示。

图5 不同低速泵转速输入曲线
由仿真和试验曲线可知,在不同定量泵转速输入下,变量马达转速数值基本保持不变,仅在(1500±3)r/min范围内波动,同时满足(1500±6)r/min的转速控制要求。这是由于变量马达摆角基准与定量泵转速成正比关系,在补偿摆角小范围作用下,斜盘摆角几乎仍与定量泵转速成正比关系。因此,在恒流源状态下变量马达转速依然保持不变。

图6 不同低速泵转速输入时变量马达转速输出曲线
3.2 低速泵波动转速下的变量马达恒转速输出分析
由于实际风速是实时波动的,导致定量泵转速也处于变化状态,因此需要探究波动风速对变量马达恒转速输出的影响[16],验证转速控制方法的抗干扰性能。
仿真和试验时,给定发电机负载功率保持不变,利用图7a所示定量泵波动转速模拟实际风速变化,得到变量马达输出转速变化如图7b所示。由图可知,在定量泵转速输入变化时,变量马达输出转速会随着定量泵转速输入变化趋势在小范围内波动,其值稳定在(1500±4)r/min内,满足(1500±6)r/min的转速控制要求。可见,在定量泵波动转速下,变量马达转速依然保持在有效范围内,能够实现有效并网发电,其转速控制方法在低风速下抗干扰性能良好。
4 结论
(1) 采用低速定量泵-高速变量马达增速传动闭式回路系统,在恒流源控制基础上,应用PID控制器补偿斜盘摆角方法能够实现液压风力发电机组的恒频控制;
(2) 马达斜盘摆角基准折算系数和不同低速泵转速输入对变量马达恒定输出转速的影响效果不明显;
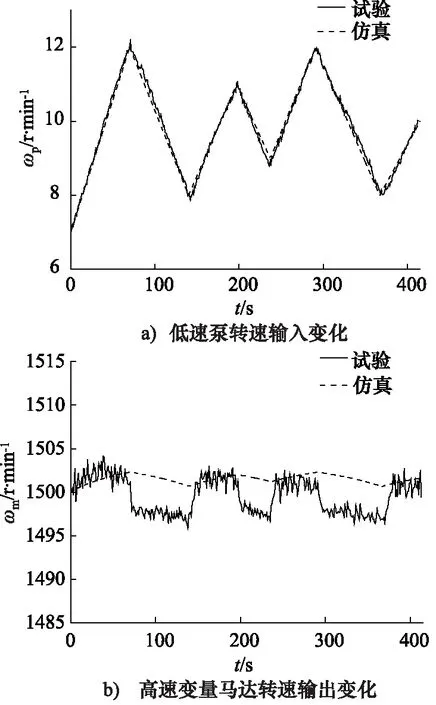
图7 低速泵波动转速下变量马达输出转速变化
(3) 在低速泵的波动转速输入下,恒频控制方法能够有效实现变量马达恒转速输出,满足并网需求,其系统稳定性好,抗干扰性能良好。
