基于Fluent的异形油箱内气泡与油液融入规律的研究
2021-04-23魏列江张吉智梁汝健张振华
李 涛, 魏列江, 张吉智, 梁汝健, 张振华
(1.兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050; 2.北京特种机械研究所, 北京 100143)
引言
液压传动系统以其功重比大、无级调速方便、成本低、体积小、使用寿命长、元器件可灵活布置、可靠性好等特点在工程机械、工业机械、农业机械、汽车等行业被广泛应用。液压油箱虽然是系统辅件,但在液压系统中不仅为系统正常工作储存足够的油液而且还起着散热、分离油液中的气泡、沉淀杂质等作用[1-2]。传统结构形式的油箱是正方体或长方体,而随着机、电、液一体化以及机械设备的小型化、结构形式多样化, 对传统的液压油箱形式提出了要求。出于节能减排、环境保护、资源利用等考虑,更加深了对新型油箱的认识与研究[3]。液压系统中的气体可以分为两类, 一类是悬浮在油液中的球状小气泡,直径在0.25~0.50 mm之间[4],一类是溶解在油液中的气泡,当外界环境的压力低于该温度下油液的饱和蒸汽压和气体分离压时,溶解在油液中的气泡就会析出,形成悬浮气泡[5]。在综合传动装置供油系统中会对油箱加压,在油液表面上部充入惰性气体,以满足液压泵在恶劣工况下的大流量吸油要求,液压油箱除具备以上储油、供油作用外,还在稳压性能方面具有很高的要求,防止泵吸空从而引起气穴、空化等现象[6]。由于液压泵的转速是泵的吸油流量的一个决定因素,当液压泵的转速不同时,泵吸入的油液流量是不同的,因此会对油液在工作管路、油箱和系统的循环率产生影响,即不同的转速代表着系统有不同的油液循环率,油液循环率不同会对油液中的气泡在油箱中的上浮产生影响;当油液循环率变大时,回到油箱的油液中气泡会因为来不及上浮、破裂消亡而被泵重新吸入系统工作,对系统工作产生不利影响。针对油液中气泡与油液的融入规律,只有少部分学者做了研究。张建生等[7]用高速摄影技术以直观、低费用的方式,研究了水中气泡的动力学特征,并与所得到的气泡图象数据进行了比较,对水中气泡的运动规律与溶解规律的研究做出了贡献。解胜等[8]利用CFX软件对新型油气混合器内部流场进行了数值仿真模拟,并通过对出口管路内油气两相流的分布情况分析,检验了其形成油气的效果,得出了在新型油气混合器内油气混合与融入规律。艾池等[9]针对钻井遇到气层时,地层气体会侵入井筒这一问题,研究时充分考虑了气泡融合特性对气泡上升速度的影响,提出了更加精确的计算气泡上升速度的方法。SKAMA S等[10]以数值模拟与实验流场可视化结果相比较的研究方法,对不同孔径的泡沫消除器通风口内的气泡与油液的融合分离现象进行了研究。SUZUKI R等[11]利用涡流消除气泡的方法,对旋流装置、内旋流场进行数值模拟与结果分析,研究了流体动力系统中夹带空气的溶液与空气的融入特性。 SHOUKRI M等[12]对大直径垂直管道中气液两相向上流动的结构,用双光探针测量法对气泡泡状流结构做了研究,提出了直径管内气液两相流中常见的空泡率。在针对闭式压力油箱的仿真、优化设计研究方面,陈溪等[13]利用液体静压方程、质量守恒和能量守恒定律,分别建立了油液和气体数学模型,创建了压力油箱自定义子模型, 并以AMESim为技术手段, 研究了压力油箱子模型的工作特性。屈武斌等[14]以减小外部空气对油液的污染为目的,设计了一种采用外置蓄能器调节油箱内部压力的闭式油箱,并通过试验验证了该闭式油箱的设计合理性。张垚等[15]提出了一种新型多功能航空液压油箱方案,并通过增压压力测试、油液加热试验和油位检测试验,验证了该新型油箱的优良性能。上述研究主要集中于不同研究对象的气泡形态和动力学特性以及压力油箱的性能研究,只有少部分文献对气液两相流中气泡与油液的溶解混入有研究。因此,以异形油箱为研究对象,研究了异形油箱在不同的充气压力、不同的液压泵转速下,油液中气泡与油液的融入关系的规律性,为液压油箱及系统的设计选型提供参考。
1 仿真计算模型与条件
1.1 仿真计算模型
对于在不同充气压力下气泡与油液融入性的规律研究,需要将异形油箱模型简化。闭式液压系统的液面以上是具有压力的惰性气体,因此在仿真过程中需要标记液相与气相所在的区域,Fluent只提供了三种标记区域的办法,如可标记六面体(指定3个方向的最大最小坐标)、球体(指定球心坐标和半径)、圆柱体(指定3个方向最大最小坐标及半径),当然也可指定所选标记区域的外部作为所标记的区域。考虑到三维异形油箱是不规则六面体,且气相所在区域为不规则六面体,因此将模型简化为二维,以便于气液相的标记;由此,可再根据气相区域所在的三维模型尺寸,建立二维模型,此时以第一种标记方法标记两相区域的内部即可。
为避免三维模型中油液从进油口到出油口之间的流动距离对气泡与油液融入性规律的影响,二维模型中进油口边界的轴向与出油口边界的径向之间的直线距离也以三维模型中相对应的距离为准;进、出油口的直径和长度,二维模型油箱的长、宽也与三维异形油箱保持一致。通常油箱液面在油箱高度的80%[1],所以标记液相高度为仿真模型油箱高度的80%,液相以上为惰性气体。
不同转速下的仿真模型采用异形油箱三维模型,计算区域为油箱进油口到油箱出油口的流体区域。
1.2 网格划分
不同充气压力下的仿真模型采用二维模型,网格类型是结构化三角形网格,在入口、出口、壁面处设置了8层网格,网格数为52579,网格质量在0.80左右;将三维模型抽取流道后,对模型进行网格划分,为保证较为精确的计算结果,对网格进行了局部细化,吸油管、回油管表面、油箱壁面设置了6层网格,计算模型的网格数为4748494, 网格质量在0.65左右。不同条

图1 不同条件下的仿真模型
件下的网格模型如图1所示。
1.3 计算条件
在使用Fluent进行仿真计算时,多相流模型采用Euler-Euler模型,因为其多适用于离散相集中于计算域的局部和有一相混合或分离的场合。采用标准k-ε湍流模型对主相(液压油)和离散相(气泡)进行仿真计算[13]。在该多相流模型下,气泡也作为连续相处理并且占用一定的体积分数。气液两相之间曳力函数选择Schiller-Naumann模型[14]。
欧拉模型方程组:
k相连续性方程为:
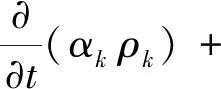
(1)

k相动量平衡方程为:
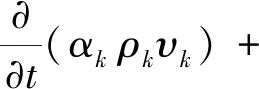

αkρk(Fk+Flift,k+Fvm,k)
(2)

混入油液中的气体是以球状气泡的形式掺混在油液中的,因此在仿真计算时,将离散相(气泡)按理想球体来处理,在多相流的分散相中设置离散相气泡直径为0.30 mm,物理属性参数按理想气体取值,具体为密度1.225 kg/m3,黏度1.7894×10-5kg·(m·s)-1。液压油为L-HM46#抗磨液压油,其物理属性参数为:密度876 kg/m3,黏度0.048 kg·(m·s)-1,将油液温度定为常值20 ℃。
在计算中设置了3个充气压力,分别为0.05, 0.10, 1.00 MPa。进口边界条件为速度进口,速度为0.56 m/s,进口气体体积分数为8%,出口边界条件为压力出口,相对压力为0。在计算中通过假定泵的转速分别为1000, 2000, 3000 r/min,拟取一个泵的排量V=400 mL/r,再根据油液密度,换算到油箱的出油口处油液的质量流量分别为5.84,11.68,17.52 kg/s。进口边界条件为压力进口,相对压力为0,进口气体体积分数为8%,出口边界条件为前所述的质量流量边界。
两种计算均采用瞬态计算,收敛残差取10-5,并对出油口处的气体体积分数进行监测,形成气体体积分数变化曲线。
需要说明的是,体积分数云图只是对于悬浮在油液中的气泡而言的,而溶解在油液中的气体体积分数是得不到体积分数云图的,以下仿真结果论述也基于此。
2 不同充气压力下气泡的分布特点及仿真分析
2.1 气泡的分布特点
图2为油箱充气压力为0.05, 0.10, 1.00 MPa下,悬浮在油液中的气体体积分数分布云图。由图2统计数据后知,充气压力为0.0, 0.1, 1.0 MPa下气体体积分数平均值分别为12%,10%,5%,充气压力为0.05 MPa时油箱内中心区域的气体体积分数达到了16%,数值相对于进口处的体积分数8%上升了50%,且气体体积分数由油箱中心向外呈同心圆形趋势逐渐降低,最外周的近似圆附近区域体积分数为2%,油箱四周壁面处气体体积分数在4%左右;充气压力为0.1 MPa 时,油箱的左下、右上、中心此3个区域的中心处气体体积分数为10%,数值相对于进口处的体积分数8%上升了20%,且均由各个区域中心数值向外呈近似的圆形趋势逐渐降低,3个区域最外周的近似圆附近区域体积分数也为2%,四周壁面处的气体体分数为6%;充气压力为1 MPa时,油箱气体体积分数为5%,相对于进口处8%的体积分数,数值下降了37.5%。因此,三种充气压力下油箱壁面处的气体体积分数相差不大,而整体计算域的气体体积分数随着充气压力的增大而降低,以充气压力下平均气体体积分数为准,相对于进口处8%的气体体积分数,充气压力为0.05, 0.10 MPa时,体积分数分别增加了50%,25%,增大趋势减弱;而充气压力为1 MPa时,气体体积分数是减小趋势,减少了37.5%。综上所述,随着充气压力的增大, 在计算域内气体体积分数平均值增大趋势减弱,到最大充气压力1 MPa时,体积分数呈降低趋势。

图2 不同充气压力下悬浮在油液中的气体体积分数云图
2.2 仿真分析
对比不同充气压力下悬浮在油液中的气体体积分数云图可得,随着充气压力的增大,计算域的各个位置处气体体积分数均减小,且相同的气体体积分数所包含的区域面积依次减小。由此可说明:从进油口处进入油箱掺混在油液中的悬浮气泡溶解在了油液中,因此悬浮在油液中的球形气泡减少。
图3是不同充气压力下对出油口气体体积分数的平均值进行监测,进行数据处理后得到的出油口气体体积分数平均值(V0)与迭代步数(I)的变化曲线。可以看出待收敛之后,充气压力为0.05 MPa下出油口气体体积分数为25%,相对于进油口处的体积分数8%,数值上升了212.5%;充气压力为0.10 MPa下出油口气体体积分数在15%,相对于进油口处的体积分数,数值上升了87.5%;充气压力为1 MPa下出油口气体体积分数在5%,相对于进油口处的体积分数,数值下降了37.5%;由此,对图3分析后亦可得到相同的结论:随着充气压力的增加,从进口进入油箱,悬浮在油液中的气泡溶解到了油液中,因此出油口气体体积分数大幅度减小。

图3 不同充气压力下出油口悬浮在油液中的 气体体积分数平均值变化曲线
综上所述,在相同的仿真条件下,随着充气压力的增大,从进油口进入油箱内部悬浮在油液中的气体体积分数减小、油箱出油口气体体积分数平均值减小,由此可以说明悬浮在油液中的球状气泡溶进了油液,即较大的充气压力使悬浮在油液中游离的球状气泡溶进了油液,增大了油液对气体的溶解量,因此在油箱内悬浮的气泡体积分数、出油口气体体积分数的平均值随着充气压力的增大均减小。
3 液压泵不同转速下气泡的分布特点及仿真分析
3.1 气泡的分布特点
图4为液压泵转速为1000, 2000, 3000 r/min时,油箱出油口轴向切面悬浮在油液中的气体体积分数分布云图。由图4统计数据后可知,转速为1000, 2000, 3000 r/min时,气体体积分数平均值均为8%。转速为1000 r/min时,此切面中心和左侧两小部分区域的气体体积分数为8%,而切面80%的区域气体体积分数为7.8%,油箱出油口气体体积分数为7.6%;转速为2000 r/min时,出油口轴向切面85%的区域气体体积分数为8%,油箱顶部壁面处气体体积分数为8.1%,油箱出油口气体体积分数为7.9%;转速为3000 r/min时,切面60%区域气体体积分数为8%,油箱顶部壁面处气体体积分数为8.2%,出油口气体体积分数为7.9%。
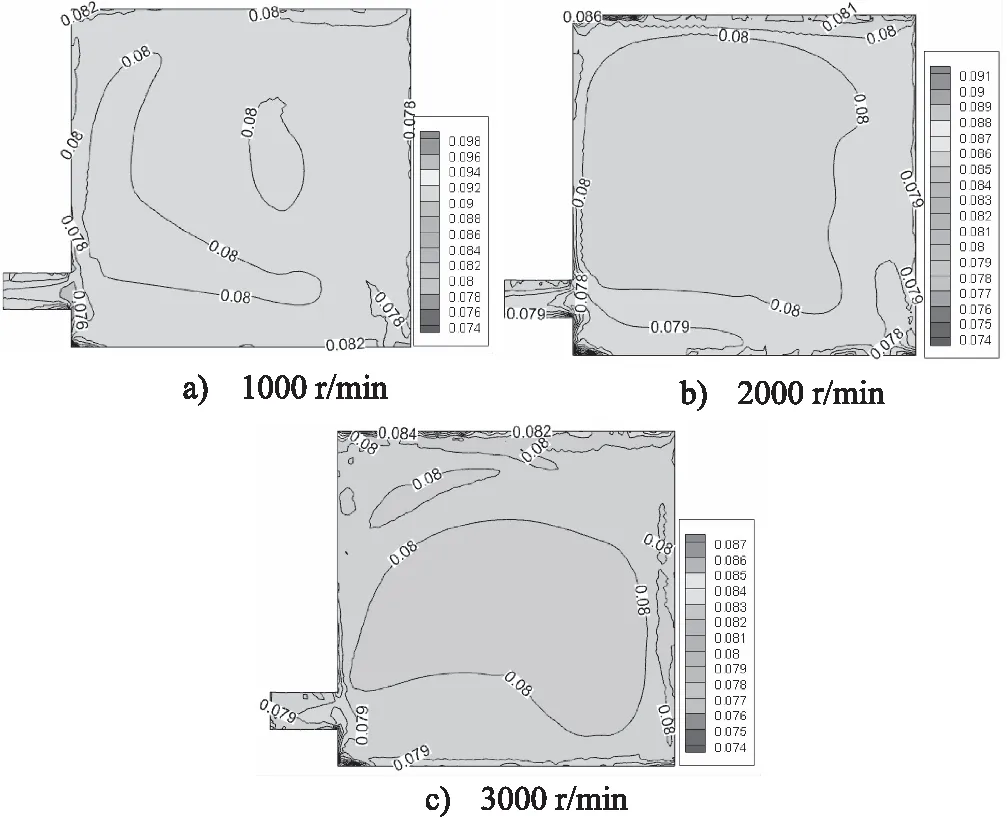
图4 不同转速下悬浮在油液中的气体体积分数云图
对比不同转速下油箱出油口轴向切面处气体体积分数云图可得,虽然转速在增大,但是油箱内的气体体积分数平均值与进口处所设置的体积分数值一致,均为8%;三种工况下四周壁面处气体体积分数均是7.9%左右;相同数值的体积分数所包含的区域面积相差不大。由此说明油箱内掺混悬浮在油液中的气泡没有溶解在油液中,即液压泵转速对气泡在油液中的溶解量没有影响。
3.2 仿真分析
图5是不同转速下对出油口气体体积分数的平均值进行监测,对数据处理后得到的出油口气体体积分数平均值与迭代步数的变化曲线,可以看出待收敛之后,转速为1000 r/min时,气体体积分数平均值是8.5%,数值上升了6.25%;转速为2000 r/min和3000 r/min时,气体体积分数平均值是8.6%,数值上升了7.5%。由图5可得,随着液压泵转速的增加,油箱出油口气体体积分数相对于进口处8%的体积分数,上升值不大,可认为基本保持不变。即液压泵的转速并不影响悬浮在油液中的气泡在油液中的溶解量,因此在出油口气体体积分数的上升值相差不大。
综上所述,随着液压泵转速的增大,油箱出油口轴向切面气体体积分数平均值与进口体积分数相同,且出油口气体体积分数平均值与进口体积分数相比,相差值很小,分别为0.5%,0.6%,0.6%。由此说明虽然液压泵转速的增大使油箱出油口处油液流量增大,但掺混在油液中的游离球状气泡在油液中不会融入和析出,对悬浮在油液中的气泡在油液中的溶解量没有影响, 此分析结果与本节第一段的分析结果一致。

图5 不同转速下出油口悬浮在油液中的气体 体积分数平均值变化曲线
4 结论
(1) 在闭式液压系统中,较大的充气压力能使悬浮在油液中的球形气泡溶解进油液,增大了油液对气体的溶解量。因此,随着充气压力的增大,油箱内部悬浮在油液中的气体体积分数减小、油箱出油口处悬浮在油液中的气体体积分数的平均值减小。
(2) 液压泵转速的增大,使油箱出油口流量变大,但掺混悬浮在油液的球状气泡,没有溶解进油液,即液压泵转速对悬浮在油液中的球状气泡在油液中的溶解量没有影响。因此,随着液压泵转速的增大,油箱出油口轴向切面气体体积分数平均值与进口体积分数相同、出油口气体体积分数平均值与进口体积分数相比,相差值很小。
