GA-BP的铁钢界面铁水温度预测

2021-04-23毕春宝张亚竹石少元郭亚祥

材料与冶金学报 2021年1期

毕春宝，张亚竹，石少元，郭亚祥，黄军，2

（1.内蒙古科技大学能源与环境学院，包头 014010；2.内蒙古自治区高效洁净燃烧重点实验室，包头 014010）

铁水作为炼钢的基本原料，其自身的物理热与化学热是转炉炼钢的基本热量来源，在化学热一定的条件下，铁水入转炉的温度直接反映了具有物理热的多少，较高的铁水温度有利于转炉炼钢工艺生产的稳定顺行和减少能源消耗，铁水温度过低则会影响炼钢的吹氧作业、硫元素和磷元素的氧化过程及熔池的温升速度，从而影响冶炼钢种的质量或带来安全问题.此外，铁钢界面铁水温度直接影响了KR工序的操作时间、熔剂消耗量和脱硫效果等.因此，快速准确地获取铁钢界面的铁水温度对后续KR和转炉炼钢具有重要意义［1-2］.

为获取铁钢界面的铁水温度，较为常用的方法是以传热学理论为基础建立机理模型，以此实现铁水温度的预测.向顺华等［3］采用二维模型对宝钢铁钢界面铁水运输过程的温度变化进行了模拟计算，并建立了温度预报离线模型.杨圣发等［4］模拟了铁水运输过程的温度变化和鱼雷罐砖衬的温度分布，进而利用统计方法实现了铁水温度在线预测.王君等［5］开发了3种不同铁水运输工艺条件下的温降模型，并分阶段计算了铁水温度.虽然上述方法可以计算铁钢界面的铁水温度，但针对长流程、多工序的生产过程，其影响铁水温度的因素较多且数值波动范围较大、耦合性较强，因此导致机理模型计算周期较长、精度受限.企业内数据的不断积累和神经网络算法的不断应用为铁钢界面铁水温度预测提供了一种新的思路.任彦军等［1］基于沙钢“一包到底”模式建立了BP（back propagation）神经网络 LM（Levenberg-Marquardt）算法的高炉—转炉界面铁水温度预报模型.汪森辉等［6］建立了 ELM（extreme learning machine）算法的铁钢界面铁水温降预测模型.由于神经网络具有较强的非线性和自适应学习的能力.因此，基于神经网络的数据驱动模型在一定条件下更适用于铁钢界面铁水温度的预测.

综合上述分析并结合前人研究内容，本文依托某钢铁企业EMS（energy management system）数据系统收集了铁钢界面生产数据67 855条.采用较大样本建立预测模型的目的是提高模型的预测精度和泛化能力.结合传热机理与现场数据采集情况，本文筛选出7个对铁水温度有影响的关键因素，并设计了基于遗传算法（genetic algorithm，GA）优化的BP神经网络（GA-BP）预测模型.模型可实现在不同运转周期下铁钢界面铁水温度的快速预测，为后续炼钢厂的生产和优化提供参考.

1 铁水温度影响因素

本研究所涉及的铁钢界面的工艺流程如图1所示.根据具体工艺流程，分析并筛选出对铁钢界面铁水温度有影响的关键因素.

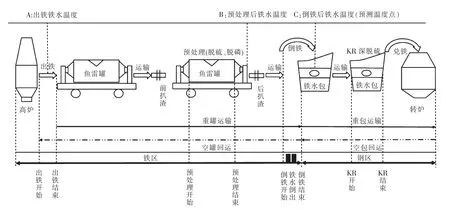
图1 铁钢界面工艺流程图Fig.1 Flow chart of ironmaking and steelmaking interface

参照图1所示的铁钢界面生产工艺流程，将其分为两大区段，分别为铁区和钢区，其影响铁钢界面铁水温度的因素有两部分，分别为工序操作过程和鱼雷罐周转过程［7］.工序操作过程对铁水温度的影响包括高炉出铁、铁水预处理、前（后）扒渣和倒铁工序，且影响程度与工序操作时间和本身操作状态有关.由于该企业二次出铁率仅约16%，且由于二次出铁会增加建模复杂性.因此，本文中高炉出铁工序不包含二次受铁情况，故高炉出铁工序选择出铁时间和出铁铁水温度作为影响铁钢界面铁水温度的关键因素.铁水预处理工序选择预处理时间和预处理后铁水温度作为关键因素.由于前（后）扒渣工序仅发生在少数鱼雷罐中.因此，本次建模不考虑扒渣操作所带来的影响.根据现场统计结果显示，倒铁工序中铁水倒出时间很短，即在3 min以内完成，无明显波动，并且由于企业生产数据中仅记录了倒铁工序总时间，无法准确获取铁水倒出时间.因此，建模时未将铁水倒出时间作为关键因素.鱼雷罐周转过程对铁钢界面铁水温度的影响主要体现在铁水等待或运输过程中的对流换热、辐射换热和罐衬蓄热，而周转时间是衡量换热量的重要参数.因此，选择鱼雷罐周转过程中的重罐时间和空罐时间作为关键因素.此外，随着铁水质量的增加，铁水周转过程的温降减小，而铁水温降减小的程度随铁水质量的增加而逐渐减弱［8］.

通过对铁钢界面工艺流程的分析，筛选了出铁时间X1、预处理时间 X2、重罐时间X3、空罐时间X4、出铁铁水温度X5、预处理后铁水温度X6和铁水质量X7为影响铁钢界面铁水温度的关键因素.

2 数据预处理

2.1 异常值检测

EMS系统中的数据会因为某些原因出现异常，如数据缺失、超出正常范围和数据链关联错误等.数据异常会导致模型精度变低，甚至建模失败，因此在构建模型前应进行异常值处理.本文选取的7个关键因素的约束条件由现场实际生产情况确定，其正常波动范围如表1所示.采用直接剔除异常值的方法，共获得8 000组铁钢界面实际生产数据用于构建预测模型.

表1 关键因素及其波动范围Table 1 Key factors with fluctuation range

2.2 归一化

数据归一化的目的是消除参数之间的量纲影响，同时防止使用神经网络构建预测模型时，出现权值调整放缓而导致训练时间过长，甚至建模失败的问题.本文采用“最大-最小归一化”方法将建模数据做线性变换映射至［-1，1］区间.归一化公式如下：

式中，Xi为关键因素的原始值；Xmin和Xmax分别为Xi的最小值和最大值；X′i是原始数据归一化后的值.

3 算法描述

3.1 遗传算法

遗传算法（GA）是一种模拟生物自然选择和自然遗传机制的概率搜索算法，遵循适者生存、优胜劣汰的进化法则.在遗传算法实现时，需要通过编码完成种群的初始化，进而通过适应度函数评价种群中的个体对外界环境的适应性，以大概率选择适应度大的优良个体.由被选择的优良个体组成新的种群，且新个体经过交叉和变异等操作后，产生下一代优秀个体.经过多次迭代后，最优个体的适应度达到给定的阈值或迭代次数达到设定的最大值时，算法终止计算［9-11］.

3.2 BP神经网络

BP神经网络是一种多层的前馈神经网络，网络拓扑结构与多层感知器相同.然而BP神经网络强调网络采用误差逆传播算法进行权值和阈值调整，即网络进行学习时，训练数据从输入层经过隐藏层至输出层正向传递，此后将沿着误差减小的方向，从输出层经过隐藏层逐层向前反向修正神经网络的连接权值和阈值，最终使误差减小［12-13］.本文所建立的BP神经网络拓扑结构如图2所示.

图2 BP神经网络拓扑结构Fig.2 BP neural network topology

BP算法实现过程如下：有训练样本集D=｛（x1，y1），（x2，y2），…，（xm，ym）｝，其中 xi=［X1，X2，X3，X4，X5，X6，X7］T，表示输入层输入变量有7个，即7个输入神经元.假定神经网络隐藏层神经元个数为q，bh是隐藏层第h个神经元的输出值，输入层神经元与隐藏层第h个神经元之间的连接权值用Vih表示.本文中输出层的输出变量仅有1个，即1个输出神经元.隐藏层第h个神经元与输出层神经元的连接权值表示为Wh.隐藏层第h个神经元的阈值为γh，输出层神经元阈值为θ.对于单一训练样本（xk，yk），计算可得隐藏层第h个神经元的输出分量为：

式（2）中，f1为隐藏层神经元使用的传递函数.

计算可得输出层的输出分量为：

式（3）中，f2为输出层神经元使用的传递函数.

网络经过训练数据的正向传递后，得到一个总体误差E：

式（4）中，yi是数据集的实际值为神经网络的输出值.

沿着误差梯度下降的方向，不断更新连接权值，更新公式如下：

式（5）和式（7）中，Wh（n+1）与 Vih（n+1）分别为网络第（n+1）次更新后的连接权值；式（6）和式（8）中，η为神经网络学习率，取值在0到1之间，其中负号的含义为网络以负梯度方向对权值和阈值进行调节，使误差逐渐降低.

3.3 GA-BP神经网络

BP神经网络因结构简单、具有良好的自适应性和泛化性而在各领域得到了广泛的应用.理论上，三层BP神经网络可以逼近任意非线性函数.但是，由于BP神经网络的初始权值和阈值一般是随机选择的，因此，初始化参数会影响网络训练，进而影响输出.GA-BP神经网络能够优化初始权值和阈值，使模型更好地进行样本预测［14］.GA-BP神经网络算法流程如图3所示［15］.

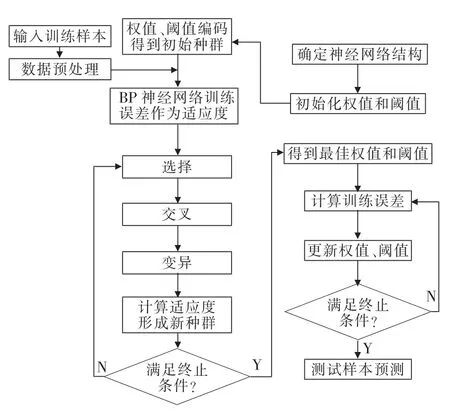
图3 GA-BP神经网络流程Fig.3 Flow chart of GA-BP neural network

4 模型构建与仿真结果

4.1 预测模型构建

本文构建一个三层神经网络，选取出铁时间、预处理时间、重罐时间、空罐时间、出铁铁水温度、预处理后铁水温度和铁水质量为输入变量，铁钢界面铁水温度为输出变量.由于隐藏层节点数对神经网络模型性能有较大影响，若节点数量过多，可能导致模型训练时间过长.目前确定隐藏层神经元个数最普遍的方法是由经验公式“试凑”获得最佳值［16］，以公式（9）为依据可知：

式中，M为隐藏层神经元个数的估计值；n和m分别为输入层和输出层神经元个数；a是［1，10］之间的常数.通过对比不同取值的隐藏层神经元个数可得，当M=12时，模型的性能最佳.最终确定了预测模型的网络拓扑结构为7×12×1.

神经网络在输入层与隐藏层之间、隐藏层与输出层之间分别选用tansig和purelin函数作为传递函数，并采用trainlm函数对网络进行训练.设定网络最大迭代次数为1 000次，网络训练目标误差为0.001，学习速率为0.05.遗传算法种群规模设置为50，个体维度=输入层神经元个数×隐藏层神经元个数+隐藏层神经元个数×输出层神经元个数+隐藏层神经元个数+输出层神经元个数=109.进化代数为200，交叉概率为0.5，变异概率为0.1.随机选取样本总体的80%作为训练集数据，剩余20%作为测试集数据，构建铁钢界面铁水温度预测模型.

4.2 预测结果分析

基于GA-BP神经网络模型，利用测试集数据对铁钢界面铁水温度（图1中C点对应的铁水温度）进行预测.本文选取命中率（hit rate，HR）、平均绝对百分比误差（mean absolute percent error，MAPE）和均方根误差（root mean square error，RMSE）作为模型预测结果的评价指标，如下式（10）～（13）所示.将预测模型连续运行10次，取上述评价指标的平均值，并将其与BP神经网络模型进行对比，如表2所示.图4为GA-BP模型对测试集数据的预测结果.

表2 模型评价结果Table 2 Model evaluation results

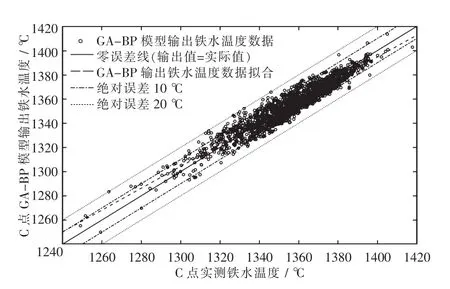
图4 GA-BP模型预测结果Fig.4 Prediction results of GA-BP model

根据表2可知，BP神经网络预测模型的MAPE为0.43%，RMSE为7.26℃；GA-BP神经网络预测模型的 MAPE为 0.39%，RMSE为6.41℃.由此说明了GA-BP神经网络模型对铁钢界面铁水温度的预测误差更小，模型也更稳定.结合表2和图4可以看出，经GA-BP神经网络模型预测的铁水温度，其预测值与实际值吻合良好.误差在10℃范围内，GA-BP预测模型的命中率达到了89%；误差在20℃范围内，GA-BP预测模型的命中率达到了99%.此外，将GA-BP预测模型的输出值与实际值做线性拟合，相关系数为0.93.综上所述，本文构建的GA-BP预测模型对铁钢界面铁水温度的预测效果更好，能够基本满足现场需求，为后续的KR工序和炼钢生产提供重要参考.