解决车辆路径问题及其变体的混合粒子群算法综述

杨观富 蔡延光

特约论文

解决车辆路径问题及其变体的混合粒子群算法综述

杨观富 蔡延光

（广东工业大学自动化学院，广东 广州 510006）

通过对车辆路径问题的分析总结，得出启发式算法在解决车辆路径问题具有优越性的结论，并以混合粒子群算法为代表，详细阐述混合粒子群在不同车辆路径变形问题中的应用。最后指出车辆路径问题和混合粒子群算法研究的不足与趋势，强调该问题与算法具良好的扩展性，在物流领域有广阔的应用前景。

车辆路径；启发式算法；混合粒子群

0 引言

21世纪以来，随着科学技术与电子商务的快速发展，物流行业已逐渐成为国家经济增长的重要支柱，也成为提高人民生活水平与生活质量的重要保障。同时，物流行业发展的瓶颈——车辆路径问题（vehicle routing problem, VRP）备受研究人员关注。VRP由DANTZING和RAMSER于1959年提出[1]，本意是优化亚特兰大炼油厂的运输路径。经过60多年的发展与历代研究人员的研究，其研究目的、对象和限制条件等都有极大扩充。目前，VRP已从最初的简单车辆安排调度逐步演变为运筹学中一类经典的组合优化问题，是物流管理与运输组织优化中的核心问题，也是一个典型的NP难题。

随着VRP复杂程度不断增加，传统的优化方法在解决该问题时捉襟见肘。研究人员从自然界的一些现象得到启发，利用自然界的规律设置算法，形成一系列的启发式算法，如粒子群算法、人工鱼群算法和共生生物算法等。这些算法结构相对简单，不需要研究人员具备太多相关的专业知识，调节参数较少，容易实现。但也存在计算效率低、通用性差或全局搜索能力不足等问题。随着VRP模型规模越来越大，约束条件越来越多，将算法合并得到的新算法，能较好解决这类问题，且具有较好的鲁棒性、智能性、适应性以及良好的全局搜索能力。混合粒子群算法就是其中的佼佼者。

启发式算法被提出来后受到了各国研究人员的广泛关注。本文对近年来的VRP文献进行分析总结，归纳出VRP及其变形模型；对解决各模型的算法进行归纳，着重分析混合粒子群算法目前的研究进度，并从中推断出混合粒子群算法今后的研究方向。

1 VRP及其变形

基本的车辆路径问题也称为容量限制车辆路径问题（capacitated VRP, CVRP），是指所有车辆都在中央仓库开始和结束的条件限制下，为一组相同车辆寻找到能够满足所有需求且总路线成本最小的路线集。可具体理解为若干顾客随机分布在不同区域，一组车队从仓库出发，有且仅有一次经过所有顾客位置，最后回到出发点。在这期间，每辆车不能超过最大装载能力，不能超过车辆最大行驶距离，也不能对货物进行分批配送。VRP有很多变形，下面对近年来VRP的变形进行分析总结。

带时间窗的车辆路径问题（the VRP with time windows, VRPTW）在基本VRP的基础上添加了时间限制，即强制每辆车都必须在特定的时间间隔内交付货物给顾客或从顾客处取走货物。该问题又分为带软时间窗的车辆路径问题（VRP with soft time window ,VRPSTW）、带硬时间窗的车辆路径问题（VRP with hard time window, VRPHTW）和混合时间窗的车辆路径问题（VRP with mixing time window, VRPMTW）3类。其中，VRPHTW不允许有任何的时间延迟，如Yan等[2]根据城市物流特点，建立具有困难时段的城市冷链物流两阶段配送选址路由模型；VRPSTW允许有时间上的延迟或提前，但会有相应惩罚，如李博威等[3]以软时间窗为基础，综合考虑违反时间窗、客户满意度等问题构建混合整数非线性规划模型（mixed integer nonlinear programming, MINLP）；VRPMTW允许车辆以给定的公差偏离客户时间窗，可分别在最早和最近的时间范围之前和之后为客户提供服务，节省运营成本，如丁建立等[4]考虑到航班到达的不确定性，建立地面特种作业车辆的混合时间窗车辆路径模型，有利于机场实际运营。

取货与运送问题（the pickup and delivery problem, PDP）是指货物需要从某些取货地点转移到其他交货地点。因此，根据取货与运货的回程和交接、取货与运送问题也可细分为5个部分，如表1所示。

随机车辆路径问题（the stochastic VRP, SVRP）不是单纯的车辆路径问题，而是车辆问题中的一个或者几个问题的组成，具有较大不确定性。具体分类如表2所示。

表1 PDP延伸领域

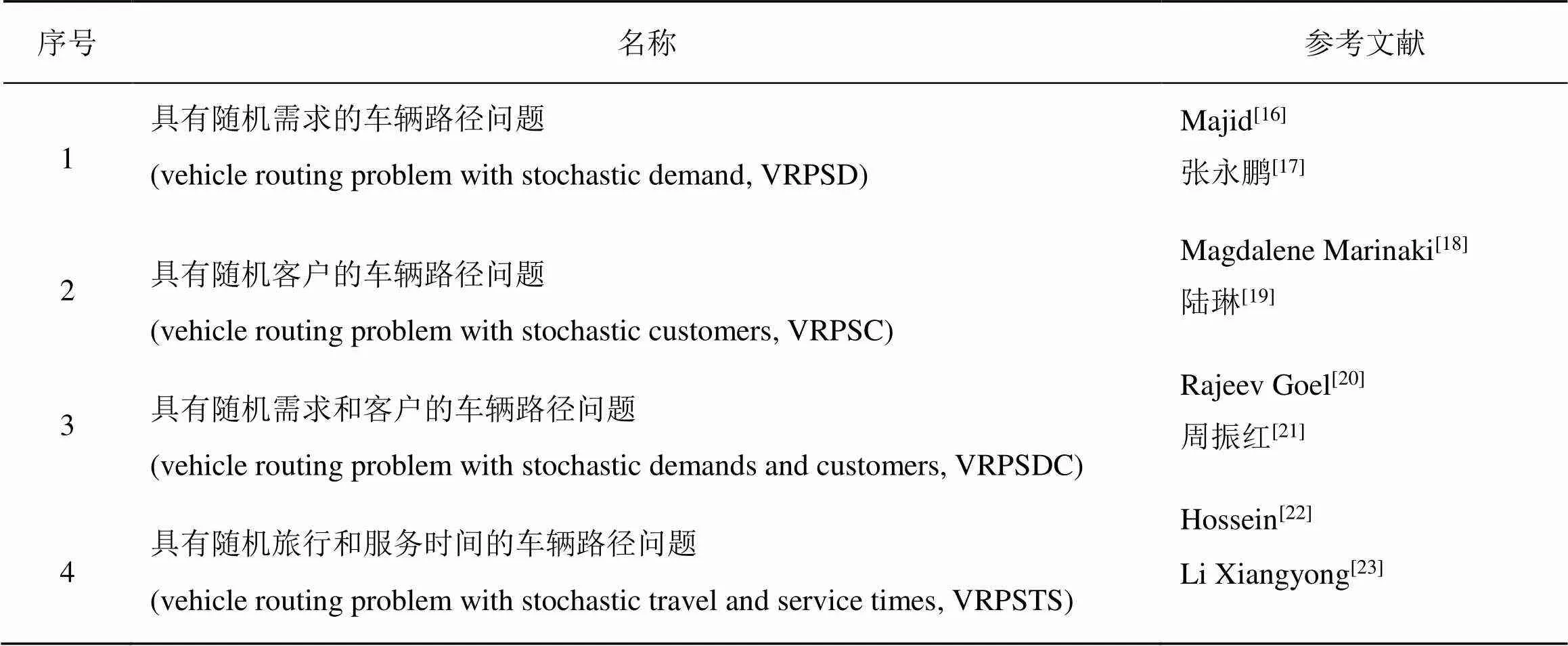
表2 SVRP分类

除上述一些常见的VRP及其变形外，还存在一些相对不常用的变形。不常用VRP及变形部分是研究人员在特定情况下提出的，即这些变形没有普适性，仅是针对相应的场景建立模型从而提出解决方法，如定期车辆路径问题、开放式车辆路径问题等，如表3所示。

表3 不常用车辆路径问题汇总表

2 混合粒子群算法

VRP的求解方法主要分为精确解法和启发式算法2类。随着VRP越来越复杂，精确解法呈指数级增长，难以满足实际应用需要。而启发式算法因具有收敛快、效率高等特点逐渐取代精确解法，成为当前研究热点。目前，研究人员的主要研究方向是构造更适用于具体场景、高质量的启发式算法，如遗传算法、模拟退火算法、蚁群算法、粒子群算法、蝙蝠算法和免疫算法等。但是随着研究的深入，VRP规模越来越大，约束条件也越来越多，启发式算法虽然具有运算简单的特点，但局部搜索能力较弱，易陷入局部最优。研究人员发现：启发式算法融合其他算法或技术特性组成的混合算法，可有效缓解局部最优问题。如混合粒子群算法就是粒子群算法融合其他算法或因子的比较有代表性的算法。混合粒子群算法最终优化目标主要为：

1）提高种群的收敛性和多样性，防止早熟收敛；

2）快速得出最优解，降低时间成本；

3）提高PSO的局部搜索性能和精度。

目前，为达到以上目标，通常有2个改进方向：1）混合进化算子；2）混合其他搜索算法，如图1所示。

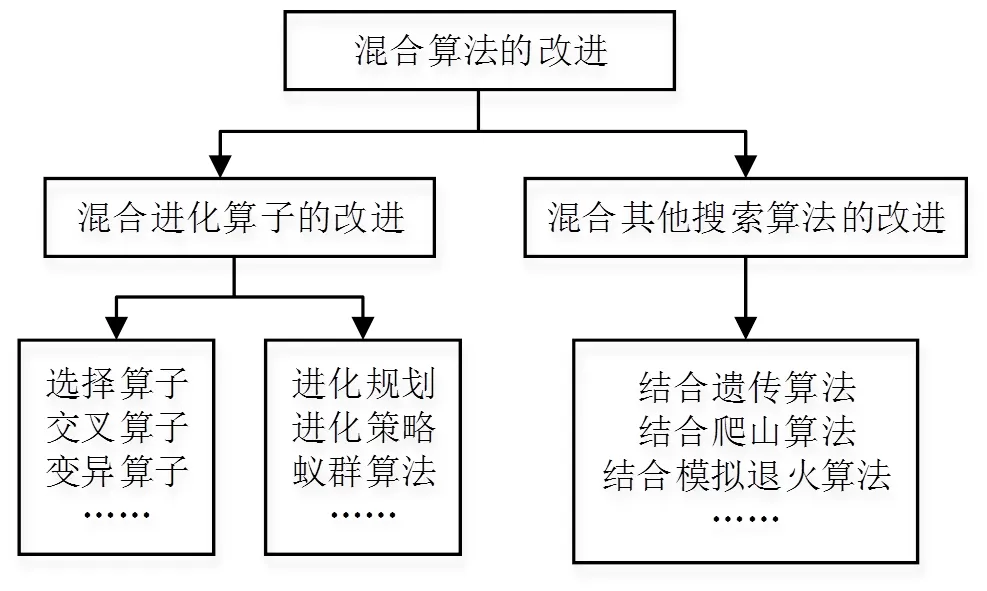
图1 混合粒子群算法混合思路

2.1 混合进化算子的改进

EBERHART等[38]将惯性系数引入标准粒子群算法，并将使用惯性权重与收缩因子的粒子群优化性能进行比较，得出适当选择惯性权重可有效提高粒子群优化性能，从此开始混合进化算子的研究。周驰等[39]在进行窄巷道仓储三维拣选时，将动态惯性权重的思想引入粒子群算法，并在优化过程中使用交叉算子和变异算子，实验证明，该混合粒子群算法在解决三维拣选问题上效果比遗传算法好。KENNEDY等[40]在寻找使粒子群起作用特性时，去除粒子群的一些传统特征，通过消除速度公式来修改粒子群算法。梁旭[41]等将混沌优化的思想引入粒子群，在解决在线检测与路径规划方面比蚁群算法的效果好。ANGELINE[42]将优胜劣汰的思想转化为选择算子，并将其引入粒子群算法，根据适应度值的好坏，将最差的一般粒子淘汰，保留最差粒子的个体极值，提高算法的全局搜索能力与精度。MENG[43]等以交叉搜索作为进化催化剂，提出新型交叉搜索的粒子群算法，该方法通过在相反方向执行不同的交叉操作，在每一代中复制大量的中度解，水平交叉搜索提高粒子群算法的全局搜索能力，与水平交叉搜索不同，垂直交叉搜索用于保持群体多样性，并且也是避免局部最优问题的有效手段，大量实验结果表明，与大多数其他最新的粒子群变体相比，交叉粒子群算法具有更好的搜索性能。

2.2 混合其他搜索算法的改进

葛宏义等[44]结合粒子群算法与模拟退火算法，根据粮食运输分布分散、数量多等特点建立VRPTW模型，取得较好效果。马艳芳等[14]利用模糊随机理论的特点解决环境不确定性，结合粒子群算法求解VRPSPD。楚学伟[45]为提高车间效率将粒子群与模拟退火和遗传算法结合，对DVRP进行建模求解，实验效果比离散粒子群算法好。陆琳[46]将导引式局部搜索理论引入种群搜索中，提出新的混合粒子群算法解决VRPSC，证明了混合粒子群算法的有效性。The Jin Ai等[47]提出粒子群不同的编码方式，结合模拟退火算法对CVRP进行建模编码，并比较2种不同编码方式对优化结果的影响。MIRHASSANI[48]在解码方法中以降序构造顾客位置向量，实现一种真值版本的混合粒子群算法解决OVRP，该算法在可行性条件下，给每个客户分配一条路线。Yannis Marinakis[49]将局部搜索策略应用于粒子群算法，针对VRPSD进行求解，并与差分进化算法和遗传算法进行对比，验证其优越性。Du Jiaoman[50]综合考虑危险材料的需求和潜在威胁，提出4种基于模糊仿真的混合粒子群算法，解决了存有危险材料的多仓库物流车辆路径问题。李和洋[51]根据库存路径和车辆路径的关系，同时考虑不同型号车辆的运输能力，设计双层遗传算法，结合粒子群算法对PVRP和VRPLC提出全新算法，为相关企业的库存路径优化决策提供参考。

3 VRP及混合粒子群问题和趋势

VRP由于不同约束条件而呈现出不同的变形。本文上述所列举的VRP变形仅是冰山一角。实际应用中，单一的变形可根据现实情况调整，从而衍生出更符合实际应用的模型，而不是把研究目标过于理想化，仅仅注重成本最小或路径最短。此外，上述车辆路径变形不是独立存在的，存在着各种变形问题的组合，最终还是归结于实际情况，不能拘泥于某一个特定的模型。随着物流业的发展，VRP更加复杂，规模也越来越大，必然会出现更多路径问题的组合，甚至全新的车辆路径模型。

混合粒子群算法以其优越的性能而被广泛应用于VRP的研究。值得一提的是，不是所有的VRP及其变形都适合使用混合粒子群算法进行求解，遗传算法、共生生物搜索算法或混合遗传算法等更适合于某些模型的求解，对于其他启发式算法的组合性能问题将是下一个优化VRP需要考虑的问题。此外，粒子群算法在混合过程中，惯性权重、混合算法的选取也是一个值得研究的方向。混合算法操作过程中，以哪个算法为主导，何时应用所需算法也是亟需解决的问题，如粒子群混合遗传算法中，并行式混合与串行式混合对模型的求解有很大不同。推而广之，在与其他算法混合时，需要考虑到混合的时机选取，混合方法选取等问题。随着VRP复杂程度增加，多种启发式算法的混合使用已成为趋势，多种混合算法所衍生出来的问题也会越来越多，需要更多的实验来佐证算法的可行性。

4 结语

本文通过对近年来研究车辆路径问题的文章进行分析，总结出多种目前正在研究的模型。同时对求解车辆路径问题的2种解法进行对比，得出启发式算法是目前较为合理解法，并引出一系列常见的启发式算法。在此基础上以混合粒子群算法为代表，详细分析总结了混合粒子群在车辆路径问题上的应用。最后指出车辆路径问题以及混合粒子群算法的研究问题及发展趋势，表明车辆路径问题及混合粒子群算法研究的必要性以及具有良好的应用前景。

[1] DANTZIG G B, RAMSER J H. The truck dispatching problem [J]. Management Science, 1959,6(1):80-91.

[2] Yan Liying, Grifoll Manel, Zheng Pengjun. Model and algorithm of two-stage distribution location routing with hard time window for city cold-chain logistics[J]. Applied Sciences, 2020, 10(7):2564.

[3] 李博威,户佐安,贾叶子,等.带软时间窗的同时取送货车辆路径问题研究[J].工业工程,2020,23(5):75-81.

[4] 丁建立,孙彩苹,李永华,等.基于混合时间窗的航空货运车辆动态调度模型[J].计算机与数字工程,2016,44(5):838-842.

[5] Mauricio Granada-Echeverri, Luis Carlos Cubides, Jésus Orlando Bustamante. The electric vehicle routing problem with backuals[J]. International Journal of Industrial Enginee- ring Computations, 2020, 11(1):131-152.

[6] 刘涛. 基于改进遗传算法的H公司VRPB优化研究[D].邯郸:河北工程大学,2013.

[7] Javier Belloso, Angel A Juan, Enoc Martinez, et al. A biased‐randomized metaheuristic for the vehicle routing problem with clustered and mixed backhauls[J]. Networks, 2017, 69(3):241- 255.

[8] Andreas Bortfeldt, Thomas Hahn, Dirk Männel, et al. Hybrid algorithms for the vehicle routing problem with clustered backhauls and 3D loading constraints[J]. Eur J Oper Res,2015, 243(1):82-96.

[9] Henriette Koch, Maximilian Schlögell, Andreas Bortfeldt. A hybrid algorithm for the vehicle routing problem with three-dimensional loading constraints and mixed backhauls[J]. Journal of Scheduling, 2020, 23(9):71-93.

[10] 李琳,孟娇,陈莹.电子商务环境下基于预售模式的混合带回程取货车辆路径问题[J].沈阳航空航天大学学报, 2020,37(4):90-96.

[11] Olcay Polat. A parallel variable neighborhood search for the vehicle routing problem with divisible deliveries and pickups[J]. Computers and Operations Research, 2017,85: 71-86.

[12] Julian Hof, Michael Schneider. An adaptive large neighborhood search with path relinking for a class of vehicle‐routing problems with simultaneous pickup and delivery[J]. Networks, 2019,74(3): 207-250.

[13] Richard P Hornstra, Allyson Silva, Kees Jan Roodbergen, et al. The vehicle routing problem with simultaneous pickup and delivery and handling costs[J]. Computers and Operations Research, 2020,115.

[14] 马艳芳,闫芳,康凯,等.不确定同时取送货车辆路径问题及粒子群算法研究[J].运筹与管理,2018,27(12):73-83.

[15] Anirudh Subramanyam, Panagiotis P Repoussis, Chrysanthos E Gounaris. Robust optimization of a broad class of heterogeneous vehicle routing problems under demand uncertainty[J]. INFORMS J Computing, 2020,32(3):72-80.

[16] Majid Salavati-Khoshghalb, Michel Gendreau, Ola Jabali, et al. A rule-based recourse for the vehicle routing problem with stochastic demands[J]. Transportation Science, 2019,53(5):26-31.

[17] 张永鹏. 带随机需求的绿色物流多目标优化问题研究[D]. 北京:中国地质大学,2020.

[18] Magdalene Marinaki, Yannis Marinakis. A glowworm swarm optimization algorithm for the vehicle routing problem with stochastic demands[J]. Expert Systems With Applications, 2016,46: 145-163.

[19] 陆琳,蔡绍洪.一类随机顾客车辆路径问题及其算法[J].南京航空航天大学学报,2010,42(4):521-525.

[20] Rajeev Goel, Raman Maini, Sandhya Rani Bansal. Corrigendum to “vehicle routing problem with time windows having stochastic customers demands and stochastic service times: modelling and solution” [J]. Journal of Computational Science,2019,35: 111.

[21] 周振红,黄深泽.随机需求下考虑顾客策略行为的预售和退货策略[J].系统管理学报,2019,28(2):277-284.

[22] Hossein Hashemi Doulabi, Gilles Pesant, Louis-Martin Rousseau. Vehicle routing problems with synchronized visits and stochastic travel and service times: applications in healthcare[J]. Transportation Science, 2020,54(4):30-40.

[23] Li Xiangyong, Tian Peng, Leung Stephen C H. Vehicle routing problems with time windows and stochastic travel and service times: models and algorithm[J]. International Journal of Production Economics, 2010,125(1): 137-145.

[24] Raafat Elshaer, Hadeer Awad. A taxonomic review of metaheuristic algorithms for solving the vehicle routing problem and its variants[J]. Computers & Industrial Engineering, 2020,140.

[25] FITRIANA R, MOENGIN P, KUSUMANINGRUM U. Improvement route for distribution solutions MDVRP (multi depot vehicle routing problem) using genetic algorithm[J]. IOP Conference Series: Materials Science and Engineering, 2019, 528(1) 70-81.

[26] Chen Binhui, Qu Rong, Bai Ruibin, et al. A variable neighborhood search algorithm with reinforcement learning for a real-life periodic vehicle routing problem with time windows and open routes[J]. RAIRO - Operations Research, 2020,54(5): 1467-1494.

[27] LATIFFIANTI E, SISWANTO N, FIRMANDANI R A. Split delivery vehicle routing problem with time windows: a case study[J]. IOP Conference Series: Materials Science and Engineering, 2018,337(1):012042.

[28] Valeria Soto-Mendoza, Irma García-Calvillo, Efraín Ruiz-y-Ruiz, et al. A hybrid grasshopper optimization algorithm applied to the open vehicle routing problem[J]. Algorithms, 2020,13(4) :55-62.

[29] Maha Gmira, Michel Gendreau, Andrea Lodi, et al. Tabu search for the time-dependent vehicle routing problem with time windows on a road network[J]. European Journal of Operational Research, 2021,288(1): 129-140.

[30] 胡蓉,李洋,钱斌,等.结合聚类分解的增强蚁群算法求解复杂绿色车辆路径问题[J].自动化学报,DOI:10.16383/j.aas. c190872,2020:1-16.

[31] 周鲜成,王莉,周开军,等.动态车辆路径问题的研究进展及发展趋势[J].控制与决策,2019,34(3):449-458.

[32] 李俊. 带有装载约束的车辆路径优化问题研究与应用[D].西安:西安建筑科技大学,2016.

[33] Feng Liang, Zhou Lei, Gupta Abhishek, et al. Solving generalized vehicle routing problem with occasional drivers via evolutionary multitasking[J]. IEEE transactions on cybernetics, 2019.

[34] Diego Cattaruzza, Nabil Absi, Dominique Feillet, et al. A memetic algorithm for the multi trip vehicle routing problem[J]. European Journal of Operational Research, 2014, 236(3): 833-848.

[35] Sophie N Parragh, Jean-François Cordeau. Branch-and-price and adaptive large neighborhood search for the truck and trailer routing problem with time windows[J]. Computers and Operations Research, 2017,83: 28-44.

[36] Lu Chen, Yang Liu, André Langevin. A multi-compartment vehicle routing problem in cold-chain distribution[J]. Computers and Operations Research, 2019,111: 58-66.

[37] Morteza Kiani, Hany Seidgar, Iraj Mahdavi. Scheduling multi-skilled manpower with considering teams replacement and site-dependent vehicles routing[J]. Int. J. of Mathematics in Operational Research, 2017,10(1): 49-68.

[38] EBERHART R C. Comparing inertia weights and constriction factors in particle swarm optimization[C]// Proceedings of the 2000 IEEE Congress on Evolutionary Computation, La Jolla, CA. IEEE, 2002.

[39] 周驰,董宝力.基于改进混合粒子群算法的窄巷道仓储三维拣选路径规划[J].浙江理工大学学报(自然科学版),2020,43(6):823-830.

[40] KENNEDY J. Bare bones particle swarms[C]// Swarm Intelligence Symposium. IEEE, 2003.

[41] 梁旭,刘才慧.基于混合粒子群算法的在线检测路径规划[J].国外电子测量技术,2015,34(12):30-34.

[42] ANGELINE P J. Evolutionary optimization versus particle swarm optimization: Philosophy and performance differences[J]. Springer, Berlin, Heidelberg, 1998,27:50-54.

[43] MENG A B, LI Z, YIN H, et al. Accelerating particle swarm optimization using crisscross search[J]. Information Sciences, 2016,329: 52-72.

[44] 葛宏义,甄彤,车毅,等.粮食物流车辆路径问题的混合粒子群算法[J].计算机应用与软件,2011,28(7):69-71,151.

[45] 楚学伟.混合粒子群算法在动态车间调度中的应用[J].无线互联科技,2020,17(7):155-157,165.

[46] 陆琳,谭清美.一类随机需求VRP的混合粒子群算法研究[J].系统工程与电子技术,2006(2):244-247.

[47] The Jin Ai, Voratas Kachitvichyanukul. Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem[J]. Computers & Industrial Engineering, 2009, 56(1):380-387.

[48] MIRHASSANI S A, ABOLGHASEMI N. A particle swarm optimization algorithm for open vehicle routing problem[J]. Expert Systems with Applications, 2011,38(9):11547-11551.

[49] Yannis Marinakis, Georgia-Roumbini Iordanidou, Magdalene Marinaki. Particle swarm optimization for the vehicle routing problem with stochastic demands[J]. Applied Soft Computing Journal, 2013,13(4):1693-1704.

[50] Du Jiaoman, Li Xiang, Yu Lean, et al. Multi-depot vehicle routing problem for hazardous materials transportation: A fuzzy bilevel programming[J]. Information Sciences, 2017, 399:201-218.

[51] 李和洋.考虑多车型的多周期库存路径优化研究[D].大连:大连海事大学,2020.

A Survey of Hybrid Particle Swarm Optimization Algorithm for Solving Vehicle Routing Problem and Its Variants

Yang Guanfu Cai Yanguang

(School of Automation, Guangdong University of Technology, Guangzhou 510006, China)

Through the analysis and summary of vehicle path problems, the paper concludes that heuristic algorithm has advantages in solving vehicle path problems. And it also describes the application of hybrid particle swarm optimization in different VRP deformation problems in detail. Finally, the shortcomings and trends of vehicle routing and hybrid particle swarm optimization are pointed out. It is emphasized that the problem and algorithm have good expansibility and have a broad application prospect in logistics field.

vehicle routing; heuristic algorithm; hybrid particle swarm optimization

TP18; TP311.13

A

1674-2605(2021)02-0002-07

10.3969/j.issn.1674-2605.2021.02.002

杨观富，男，1996年生，硕士研究生，主要研究方向：控制与优化。E-mail:13710255965@163.com

蔡延光，男，1963年生，博士，教授，主要研究方向：网络控制与优化、组合优化、智能交通系统。E-mail: caiyg99@163.com