纯弯梁受压区声弹性系数研究

王 毅，杨 予，包 挺，徐 浩

(浙江理工大学 建筑工程学院，浙江 杭州 310018)

近年来，超声波因其具有方便、快捷、灵敏度高等优点已然成为各类工程中重要的检测手段[1- 8]。目前，已经有很多学者对超声波波速与应力之间的关系进行了研究[9- 18]。

由前人研究可知，使用超声波进行工作应力诊断的关键是获得声弹性系数，目前对于声弹性系数的研究集中于轴向拉压试件，而纯弯试件的相关研究较少。考虑到工程中许多构件处于纯弯工作状态，其声弹性系数显然具有研究价值。

本文研究了钢筋混凝土纯弯梁受压区声弹性系数的获取方法。具体步骤为：首先，通过纯弯梁的加载-声时测量实验获得受压区表层声弹性系数；其次，通过素混凝土试件轴压实验获得受压声弹性系数；最后，对上述结果进行对比分析，并总结纯弯梁受压区声弹性系数的获取方法。

本文首先介绍声弹性系数理论的发展以及声弹性计算方法；其次进行纯弯梁的加载实验和素混凝土试件的轴压实验；然后对上述声弹性系数进行对比分析。

1 声弹性理论

声弹性理论最早由Murnaghan[19]提出， Hughes等[10]在其研究的基础上推导了声弹性系数公式。在之后的研究中，Ivan Lillamand等[11]对Hughes的公式进行了一阶简化，Karen F.Bompan等[12]对比了多个混凝土试件在轴压状态下的声弹性系数。前人研究中常采用如下声弹性系数公式：

(1)

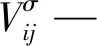
通过测量试件在不同应力状态下的声速再结合式(1)可计算出试件的声弹性系数。

2 实验过程

2.1 试件制备

为对比钢筋混凝土纯弯梁受压区和素混凝土受压试件的声弹性系数，分别浇筑了一根长宽高规格为1200mm ×100mm×150mm的钢筋混凝土梁(用于纯弯实验)和一根长宽高规格为550mm×150mm×150mm的素混凝土试件(用于单轴受压实验)。两者在制作时仅尺寸与配筋不同，材料为P.O42.5的普通硅酸盐水泥，粒径28～40mm的粗骨料以及普通河砂，配合比见表1。梁的配筋与尺寸如图1所示，在纯弯段仅配置受拉钢筋以避免受压区钢筋对波速测量的干扰，箍筋端头采用焊接方式相连，钢筋规格均为HRB400。

表1 混凝土配合比

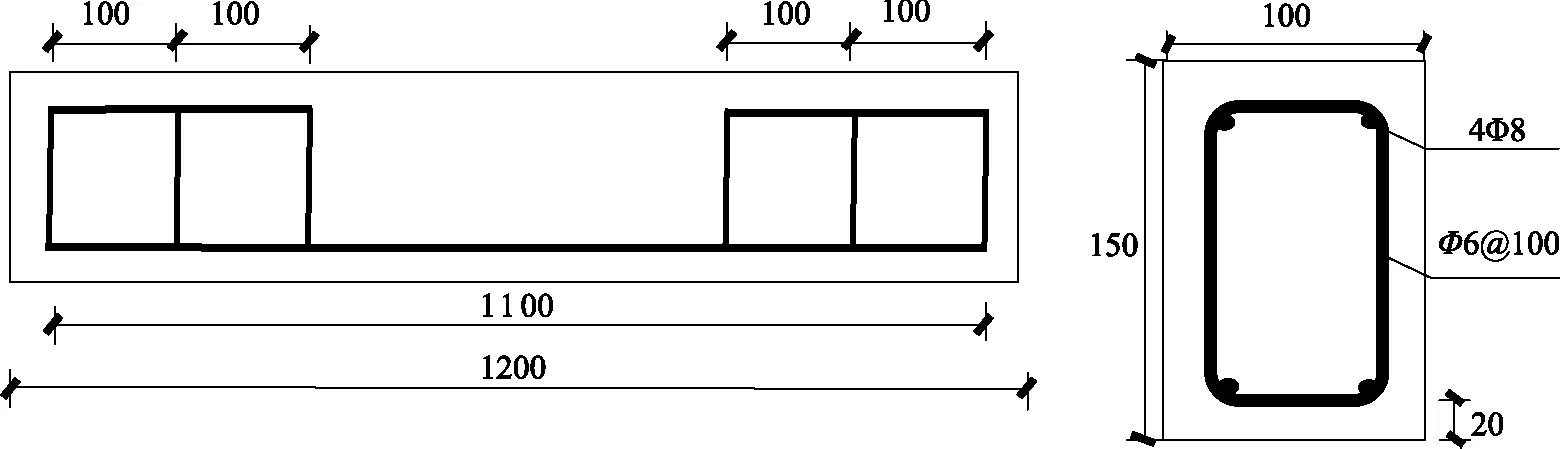
图1 梁的配筋与尺寸

2.2 实验装置

实验装置照片如图2所示。在纯弯实验中，采用图2(a)所示装置加载测量波速，加载装置由短型30t千斤顶与CP- 700液压泵构成，荷载由分配梁传给纯弯梁，采用YE2533程控读数仪控制液压泵施加的荷载。在单轴受压实验中，采用图2(b)所示装置加载测量波速，图中液压机为YAR- 2000微机控制电液伺服压力试验机。

图2 实验装置照片

2.3 测点布置

为测量试件在不同应力状态下的波速，钢筋混凝土梁纯弯实验在受压区上方布置了2个40kHz换能器，如图3所示，换能器中心距为400mm。素混凝土试件单轴受压实验在试件侧面布置了2个40kHz换能器，如图4所示，换能器中心距也取为400mm。

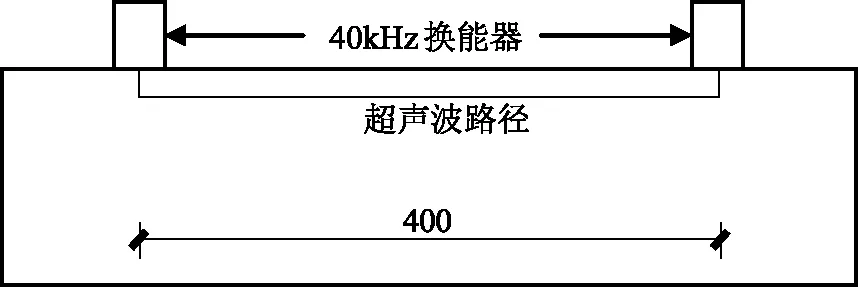
图3 纯弯实验测点布置图

图4 轴压实验测点布置图

2.4 加载与读数

钢筋混凝土梁纯弯实验采用四点弯方式加载，通过裂缝观测仪观察并控制梁表面最大裂缝宽度≤0.3mm以保证整个加载实验梁处于正常工作极限状态以内。荷载为6个等级：3000、6000、9000、12000、15000、18000N。为减少实验中微裂缝扩展对波速测量造成的影响，在测量声时前对梁进行了3轮预加载，然后再进行3轮分级加载，每级荷载稳定后测量记录声时，加载过程如图5(a)所示。

素混凝土试件单轴受压实验利用电脑控制液压机以1kN/s的速率对试件施加总共6个等级的荷载，每级应力增量为1MPa，最大应力为6MPa。加载过程分3轮预加载和3轮循环加载，每级荷载稳定后测量记录声时，如图5(b)所示。

实验数据处理方法借鉴规范CECS02：88《超声回弹综合法检测混凝土强度技术规程》，即每一级荷载的声时均读取并记录16个数据，去掉最大和最小的3个数据，取剩余数据的平均值作为该级声时，再结合测距计算出波速。

图5 实验加载过程图

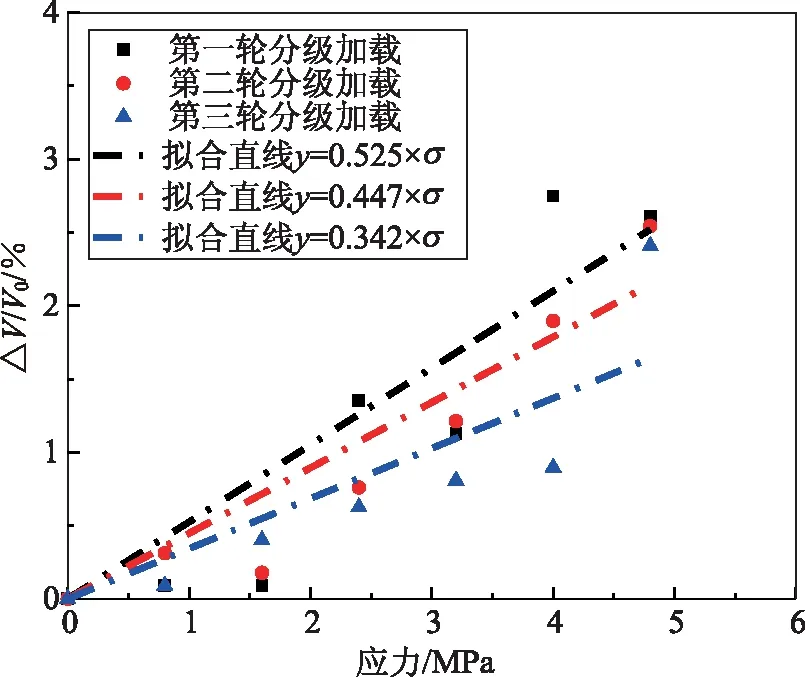
图6 纯弯声弹性系数

3 实验结果与对比分析

3.1 纯弯梁受压区声弹性系数

根据纯弯梁实验中测得的波速和式(1)可计算出声弹性系数。图6为声弹性回归系数图，x轴为根据平截面假定求出的受压侧混凝土应力，y轴为波速变化率。

图6中拟合出的直线斜率即为纯弯梁受压区声弹性系数，第三轮实验结果比前两轮小，其原因是前两轮加载过程中不断产生新的微裂缝。考虑到第三轮实验时梁的微裂缝基本稳定，受弯声弹性系数取为第三轮循环加载实验结果0.342(%/MPa)。

3.2 单轴受压试件声弹性系数

图7为依据单轴受压实验结果绘制的声弹性系数回归分析图。

图7 受压声弹性系数

由图7可知，多轮循环加载实验得到的受压声弹性系数与前人[9- 10]的研究结果接近。由于轴压实验在前两轮加载过程中新微裂缝发展速度较快，故受压声弹性系数取为第三轮实验结果0.382(%/MPa)与纯弯梁受压区声弹性系数0.342(%/MPa)非常接近。

3.3 两种声弹性系数的对比分析

纯弯梁受压区声弹性系数与素混凝土试件受压声弹性系数对比如图8所示。由图8可知，两种声弹性系数在0.3～0.6(%/MPa)之间，受弯声弹性系数的最终取值为0.342(%/MPa)比受压声弹性系数0.382(%/MPa)小0.04(%/MPa)，考虑到实验中操作以及仪器测量等原因带来的误差很难完全避免，这两个声弹性系数的差值在可接受误差范围之内。

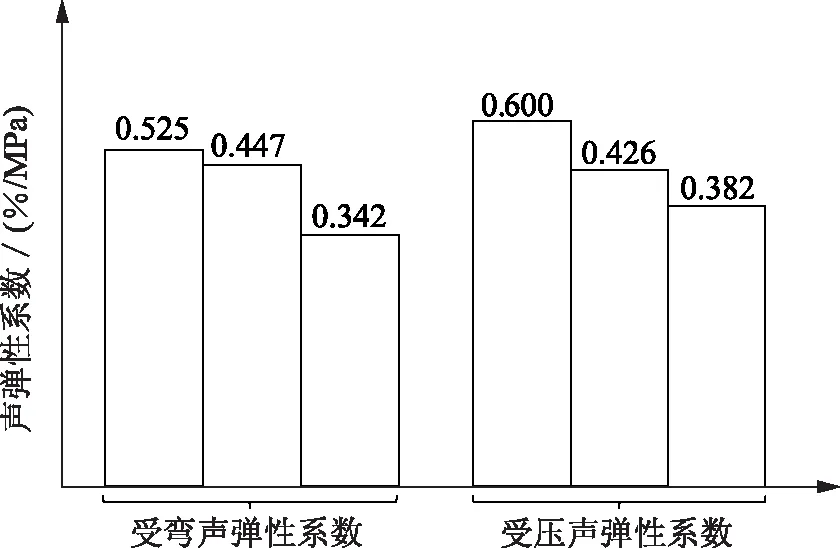
图8 声弹性系数对比

4 结论

本文通过多轮循环加载实验测量了两根试件(仅尺寸与配筋不同)处于不同应力状态下的波速，并依据声弹性理论拟合出声弹性系数。实验结果表明，受压声弹性系数为0.382(%/MPa)比受弯声弹性系数0.342(%/MPa)大0.04(%/MPa)，两种声弹性系数的差值在可接受范围之内。

结论为可通过测量素混凝土试件的受压声弹性系数来确定纯弯梁受压区的声弹性系数，测试中采用的条件应保持一致性。

本文仅对受弯及受压状态下的声弹性系数进行了研究，而试件处于其他受力状态(例如受拉、偏心受压等)时的声弹性系数是否可以采用类似方法测定，需要后续实验进行补充完善。