液化砂土地层加固措施研究与盾构隧道列车振动响应分析
2021-04-23王士民谢金池刘川昆
陈 凡,王士民,谢金池,刘川昆
(1. 西南交通大学交通隧道工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031)
引言
伴随着中国城市化进程的日益加快,地下轨道交通以其运量大、速度快、安全可靠、准点舒适等优点成为缓解大城市交通拥挤的有效方式。但当隧道穿越一些特殊复杂地层时,由于列车在长期运行过程中产生的振动荷载,可能会严重影响盾构隧道结构和运营安全,其中过量的地层沉降就是影响因素之一。例如广州地铁2号线2003年在地铁列车荷载作用下最大沉降量达16 cm,个别区段最大不均匀沉降量达到30 cm[1];上海地铁1号线部分区段隧道沉降量已超过26 cm,引发了一系列环境地质问题[2]。
国内在列车动荷载方面主要考虑结构和土层的动响应与长期沉降两方面。在结构和周围环境对列车振动荷载的动响应方面,张曦等[3]研究了隧道周围饱和软黏土的动力响应;王祥秋等[4]研究了隧道衬砌结构动力响应;杨文波等[5]采用频率响应函数FRF分析了盾构隧道衬砌结构与周围土体不同位置处的动力响应及其衰减规律;黄强等[6]基于车辆-轨道-隧道-地基模型,详细分析了地铁振动荷载对列车、轨道、地基各子模型的影响。田甜等[7]对衬砌在速度300 km/h列车荷载作用下的加速度响应规律进行了研究,经过现场衬砌振动测试和数值模型计算结果对比,验证动力计算模型的可靠性。王海龙等[8]研究了施工方法、夹层厚度及列车轴重对既有隧道衬砌结构沉降变形、振动响应影响规律,并结合现场实测数据进行对比分析。晏伟光[9]通过有限元模型计算,对不同列车轴重下重载铁路隧底结构进行动力响应分析对比。张志华等[10]以离散元为工具,借助室内三轴试验分析对比长江流域常年水位与洪水位下隧道管片的动力响应规律。
关于隧道结构长期沉降计算方面,国内外学者基于经验拟合公式提出长期动荷载作用下土层累积变形计算方法,Monismith等[11]提出加载变化指数模型,之后多位学者对该模型进行了修正。王鑫等[12]利用中厚圆柱壳理论建立隧道结构振动方程,采用Navier波动理论描述隧道周围土体,使用频散特征方程计算,并与基于薄壳理论和有限元理论的计算结果进行了对比。刘明等[13]建立了K0固结条件下软黏土的不排水累积应变与累积孔压实用计算公式,并建立了土层沉降简化计算方法。黄茂松等[14]在考虑饱和软黏土循环荷载影响下,以轴向循环塑性累积应变及第一次轴向循环塑性累积应变与围压归一化为基础,提出了计算饱和软黏土轴向循环塑性累积应变显式模型。唐益群等[15]采用有限元方法模拟列车振动引起的隧道及周围软黏土长期沉降。张东梅等[16]在研究地铁振动对隧道及地层的影响过程中,考虑了地铁列车振动与地下水渗流耦合作用。此外,娄国充[17]研究了隧道下穿对公路路基变形及铁路线路沉降的影响,雷华阳等[18]利用数值模拟研究了不同速度地铁列车荷载作用的软土层沉降特性。
目前针对盾构隧道结构的列车振动响应主要集中在单一地层,鲜少对比分析地层加固前后的隧道结构及周围地层的动力响应特性与相应的变化规律。为此,依托佛山地铁2号线,通过动三轴试验测试原状土和改良土体的动力学参数,并建立ANSYS三维计算模型,对比不同加固改良方案下隧道结构及地层应力、位移动响应特征,分析其对盾构隧道土层长期沉降的影响,为土层加固改良施工和隧道长期运营稳定提供依据。
1 工程概况
佛山地铁2号线盾构隧道下穿文登河公路涵,公路涵桩基的松木桩桩长5 m,桩径0.12 m,桩身间距0.48 m。隧道位于粉细砂、中粗砂可液化地层(图1),距离桩基净距为7.6 m,隧道埋深约16.8 m。根据沿线建(构)筑物保护分类原则规定,需做主动加固处理控制地层变形,通过采用洞内注浆加固方式,改善开挖面土体性能。区间隧道与文登公路涵松木桩平面上基本呈正交,区间隧道与桩基剖面关系如图1所示。
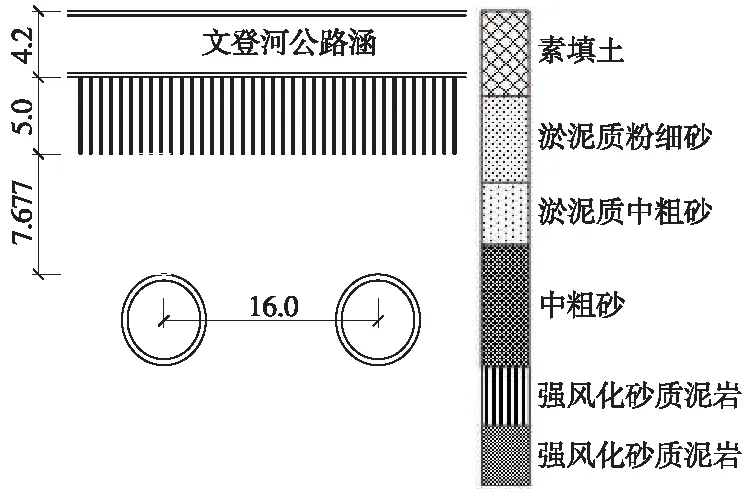
图1 区间隧道与桩基剖面关系(单位:m)
2 动三轴试验
可液化砂土在动荷载作用下土体易产生软化效应,从而丧失其原有强度而转变为液体状态,即地层强度弱化现象,其主要力学特征体现在土体强度的大幅度丧失。所以,选取可液化砂土土层的静力参数进行振动规律研究显然与实际有较大偏差,故通过模拟列车振动对砂土原状土及改良土体试样进行动三轴试验,以期获得土体在振动作用下的动抗剪强度、动阻尼比等动参数,并探究掺加超细水泥对土体动剪切模量、阻尼比的影响,为砂土的改良提供参考测试相关动力参数,同时为砂土地段的工程列车抗振设计提供理论指导。
图2为动三轴试验过程,将制备好的土样包裹橡皮膜后安装于动三轴试验机。在现场进行钻芯(φ39.1 mm×80 mm)采集土体样本,并于试验室分别对原状土样、重塑改良土样进行动三轴试验。

图2 动三轴试验过程
其中3组重塑改良土每立方米土样中分别加入强度等级为32.5的超细水泥,质量分别为200,300 kg和400 kg,用于评估佛山地铁2号线沿线液化砂土在改良前后的动力学特性。对于原状土和3种加固方案的土样动三轴试验方案如表1所示。
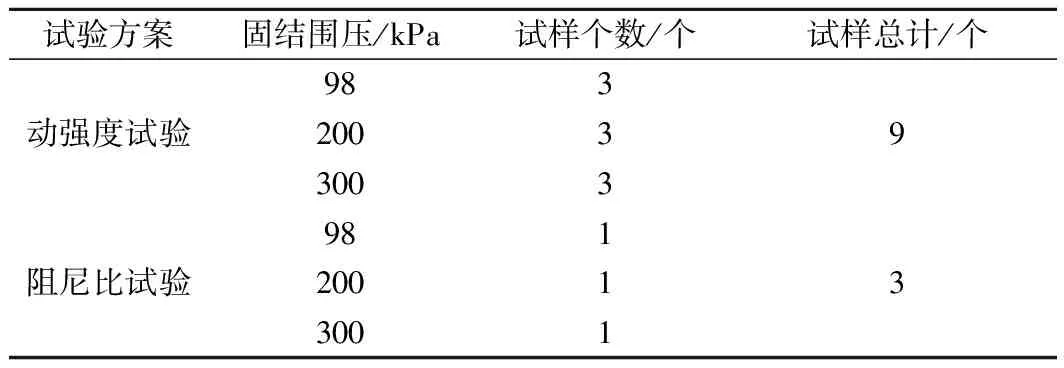
表1 动三轴试验方案
具体试验方案如下。
动强度试验:分别施加围压98,200,300 kPa进行排水固结2 h试验(固结比1.0);试验过程不排水,破坏指标以5%应变为准。
阻尼比试验:不同围压98,200,300 kPa作用下做阻尼比试验,频率为1 Hz,每种围压相应动态幅值下振动20次,具体动态幅值和对应级数如表2所示。
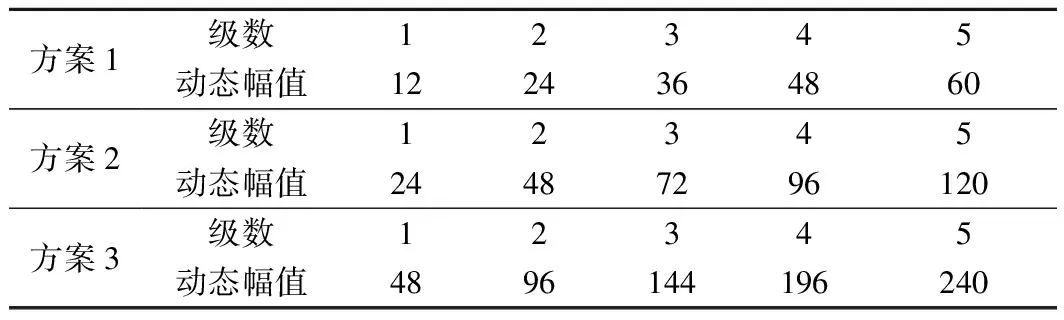
表2 阻尼比试验振动幅值 kPa
图3表示原状土样在不同剪应变下的动剪切模量比[19]。通过加固试验可知,相同应变下土体的动剪切模量比随着超细水泥掺加量的增加而增大。
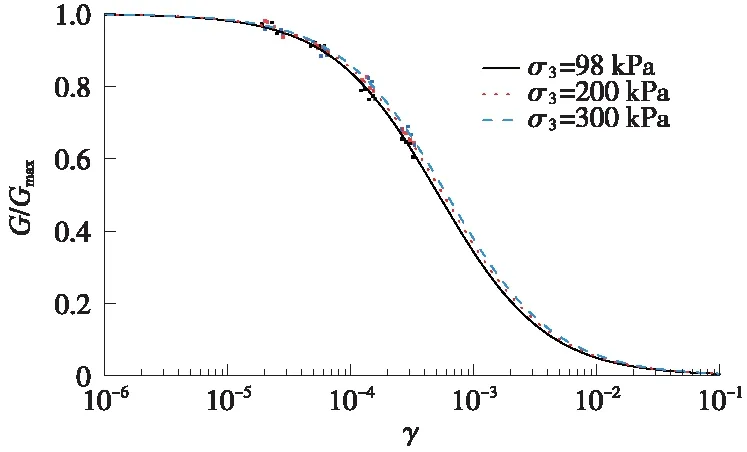
图3 G/Gmax-γ关系曲线
原状土土样的阻尼比λ与剪应变γ之间的变化关系曲线如图4所示。由图4可见,动剪切应变γ较大时,阻尼比λ逐渐趋于一个定值λmax。通过阻尼比试验可知,掺加超细水泥量越多的试样,其最大阻尼比λmax越小。
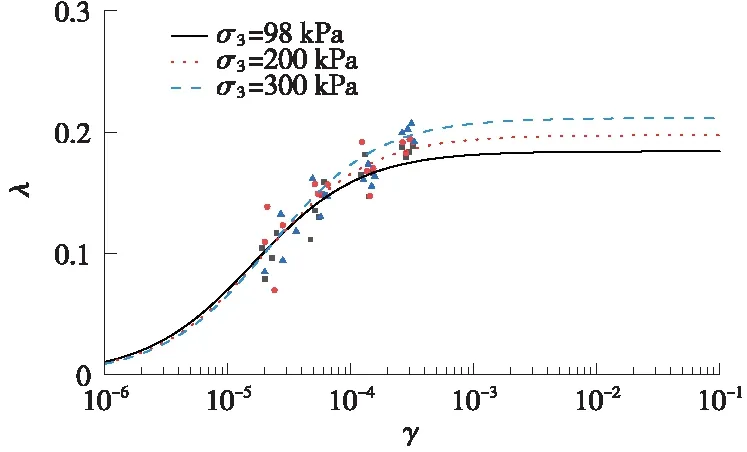
图4 λ-γ关系曲线
通过对砂土原状土和不同方案下加固土分别进行土的动三轴试验,测试土体在振动作用下的相关力学参数,如动剪切模量、阻尼比等,具体力学参数值见表3。参考动三轴试验结果,选取不同加固方案的砂土地层动参数进行数值模拟计算。
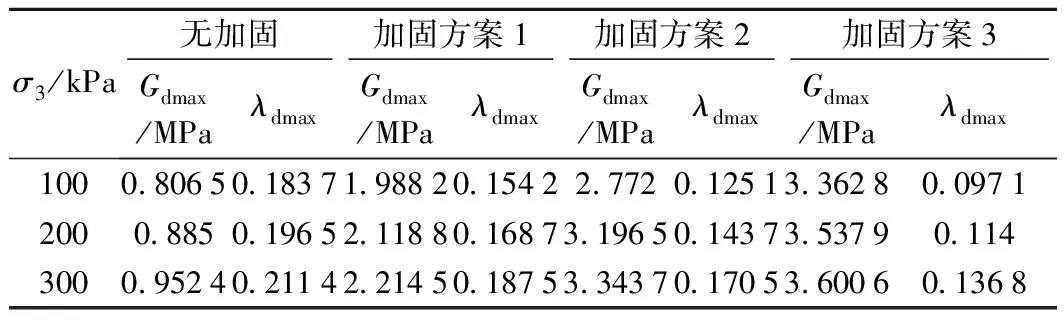
表3 动三轴试验结果
3 列车振动数值模拟
3.1 列车振动波输入
研究隧道周围土体在列车振动荷载下的沉降变形,首先要确定列车振动荷载并进行定量分析。目前,尚没有能准确反映列车荷载的数值计算方法,常用方法仍是在现场测试的基础上进行频谱分析,然后推导出列车的振动荷载表达形式。选取潘昌实等[20]提出的激振函数来表达列车荷载,即
p(t)=p0+p1sinω1t+p2sinω2t+p3sinω3t
(1)
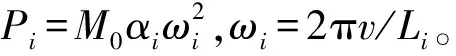
式中,P0为列车车轮静载;Pi为相应频率的振动荷载幅值;ωi为振动圆频率;M0为列车簧下质量,αi为钢轨基本振动振幅;Li为钢轨几何不平顺曲线波长;v为列车行车速度。
根据B型地铁列车参数,列车静载按空车静重计算,单轮载压力37.5 kN,取列车簧下质量M0为750 kg。根据铁路运行标准,取其典型的不平顺振动波长和相应的矢高L1=10 m,α1=3.5 mm,L2=2 m,α2=0.4 mm,L3=0.5 m,α3=0.08 mm。
目前列车运行的速度一般在30~90 km/h,选取4种列车行驶速度下的列车荷载,列车车速v取80 km/h,代入公式得到列车荷载的表达式为
p(t)=37 500+511.56sin13.96t+1 462sin69.81t+
4 678sin279.25t
(2)
沿纵向单侧的列车荷载可按下式计算
F(t)=nNp(t)l/Lc
(3)
式中,n为单侧每节车厢轮对数(取2);N为地铁列车的车辆数(取8);l为模型节点间距;Lc为地铁列车纵向长度,取160 m。
计算模型中根据地铁列车扣件上实测数据值进行加载,实际地铁盾构隧道中,扣件纵向间距一般为0.6 m,实际测量得到的扣件位置处受力随时间的变化如图5所示。根据模型节点长度将列车振动力等效到各个节点,模拟了一列地铁列车完全通过的过程,列车全车通过时间共10.235 s,共分成2 047个时间步,每个时间步间隔0.005 s。
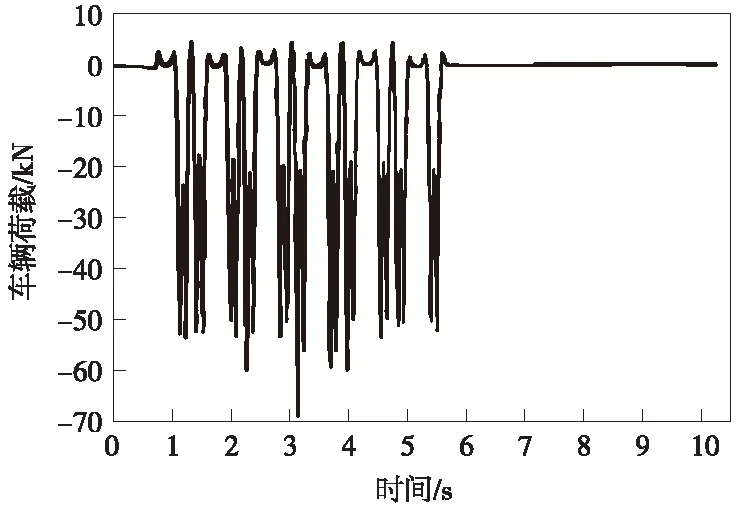
图5 列车振动荷载时程曲线
3.2 有限元模型
土体、注浆层、管片及桩基选用三维实体单元模拟,模型上边界为地面,左、右、下边界满足与隧道净距均≥3D(D为管片外径)要求,其尺寸为48 m(长)×24 m(宽)×37 m(高)。衬砌管片厚0.3 m,幅宽1.2 m,隧道埋深约16.8 m,有限元计算分析模型及模型各地层厚度如图6、图7所示。由于研究隧道运营过程中列车振动产生附加应力和位移对结构及地层环境的影响,因此,不考虑自重的作用以及盾构隧道上部桩基本身受力情况。
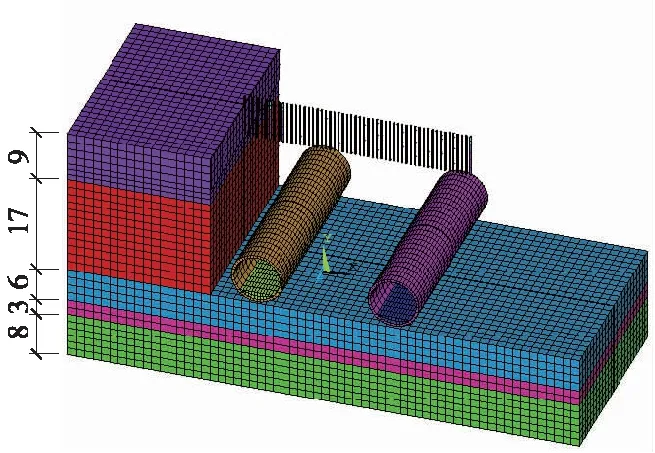
图6 隧道与桩基位置关系模型(单位:m)
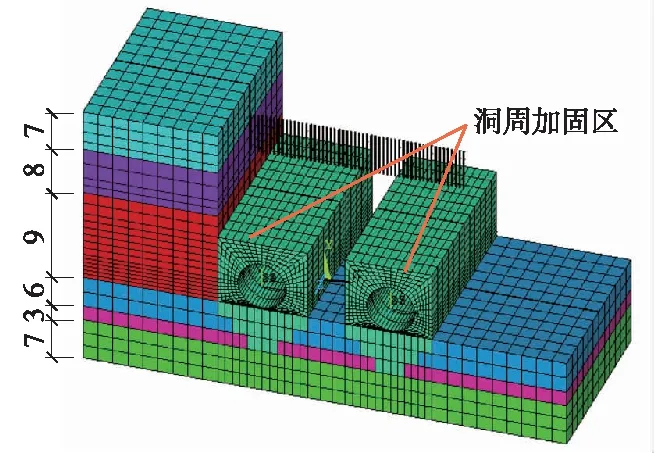
图7 盾构周围土体注浆加固模型(单位:m)
模型建立了约0.88 m厚度的道床,地铁列车轨道位于道床上部中心线两侧,轨道间距1.435 m。通过在轨道节点上施加随时间变化的等效力以模拟列车振动的作用,如图8所示。
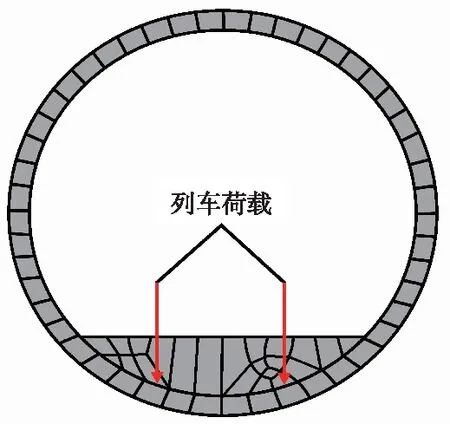
图8 隧道断面列车荷载布置示意
列车振动响应模拟计算中,根据图1地质柱状图,有限元模型中自上而下取6种土(岩)层进行计算,分别为:素填土、淤泥质粉细砂、淤泥质中粗砂、中粗砂、强风化砂质泥岩、中风化砂质泥岩。对应各地层及盾构衬砌结构相关力学参数取值见表4。
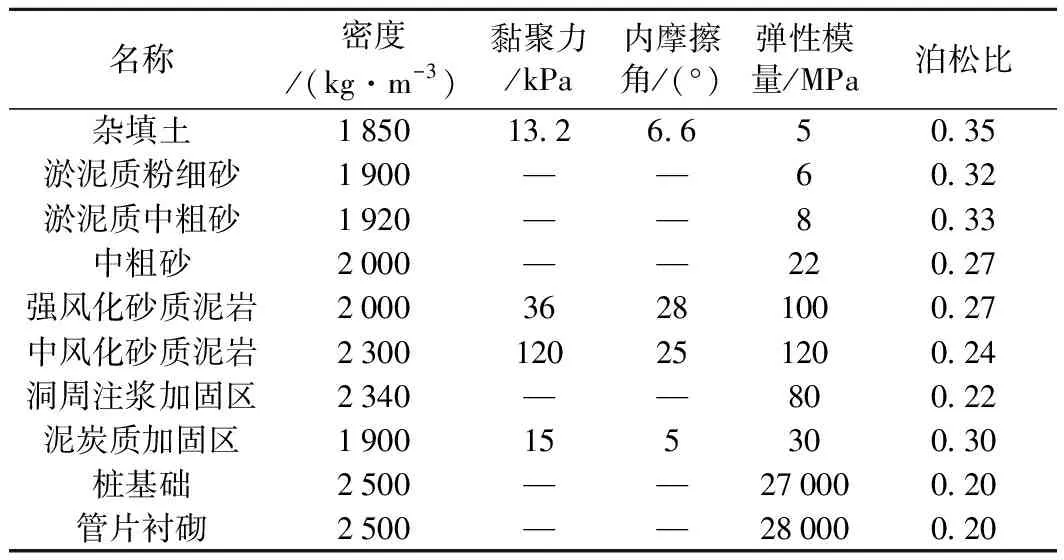
表4 土体及衬砌结构材料参数
3.3 计算监测点分布
根据列车振动波特性主要选取2.245,3.110,3.965,5.48 s时隧道的位移和应力等势线图,具体输出节点位置见监测部位,图9(a)为监视截面A-A截面,A-A截面为计算模型中间位置,由于隧道和地层结构在空间上对称,且列车作用荷载在左右两隧道的受力变形一致,因此选取了右线隧道相关节点对结果进行分析。图9(b)为隧道管片及道床在横截面的监测点分布。选取了A-A断面中竖直中心线以及隧道中心位置所在竖直线上的节点进行分析,图10为地层监测点分布情况示意。
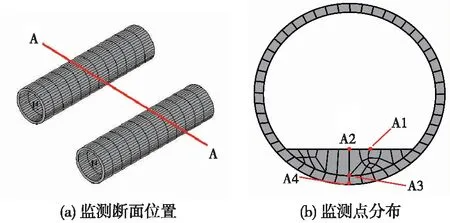
图9 监测点位置示意
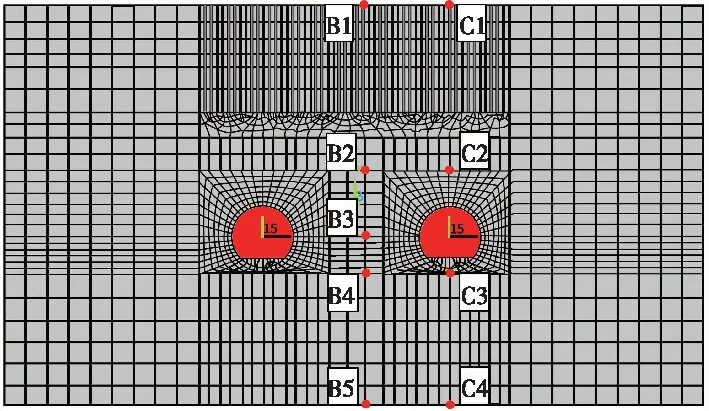
图10 地层监测点分布示意
4 列车振动响应分析
4.1 加固前列车振动响应分析
4.1.1 结构应力位移分析
通过数值模拟计算得到隧道结构未加固时,在列车振动激励时的应力。选取2.245,3.110,3.965,5.48 s时主应力结果进行对比分析。
图11为管片在各工况下结构主应力取得最大值时的结构应力云图。在列车振动荷载作用下,第一主应力的绝对值在3.965 s时均取最大值,最大拉应力值为1.53 MPa,第三主应力的绝对值在3.110 s时均取最大值,最大压应力值为1.26 MPa。第三主应力绝对值出现的位置基本位于道床以下管片位置。
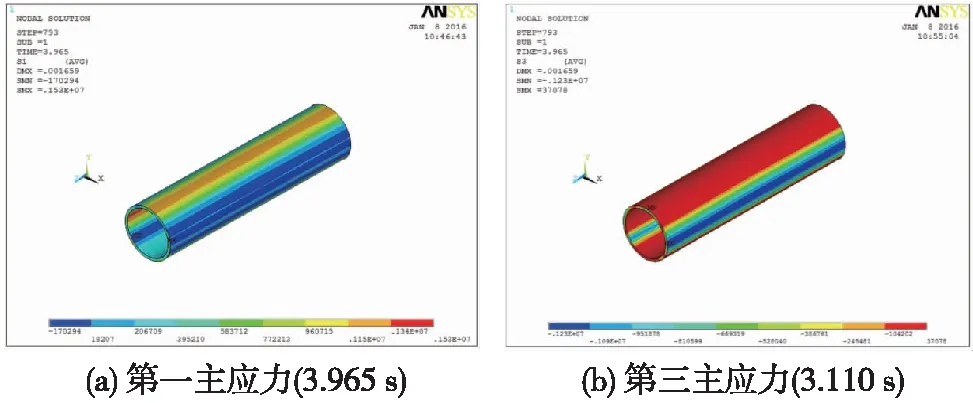
图11 管片结构在列车振动作用下应力云图
3.965 s时道床第一主应力和第三主应力在不同时刻的分布情况如图12所示。在列车振动荷载作用下,第三主应力的绝对值在3.965 s时均取最大值,最大压应力值为1.13 MPa。由图12可知,在列车荷载作用下道床结构整体受力较小,以受压为主,在道床结构的轨道位置以及道床两侧应力较集中。
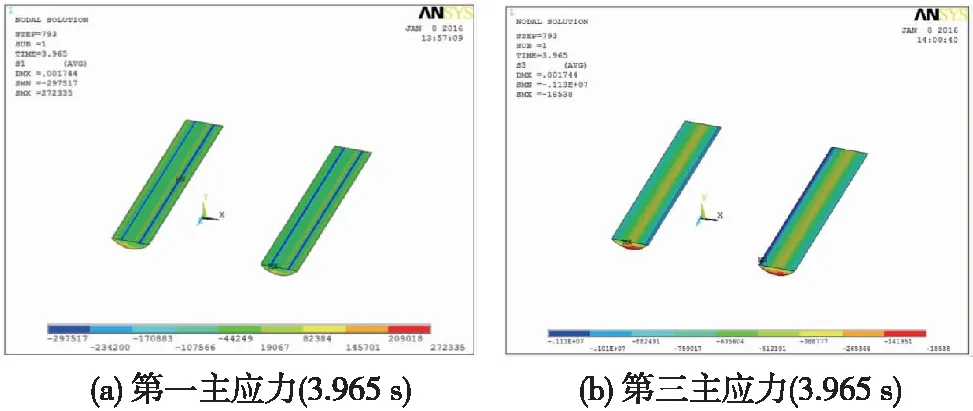
图12 道床结构在列车振动作用下应力云图
5.48 s时监测断面竖直方向及水平方向的地层位移云图如图13所示。竖直方向上,地层位移随时间变化明显,整个地层在大部分位置均产生了向下的位移,但是在局部位置地层会出现轻微隆起,隆起位置一般位于隧道两侧并距离隧道有一定距离的地表。最大地层沉降出现在5.48 s,位于隧道周围,为3.92 mm。
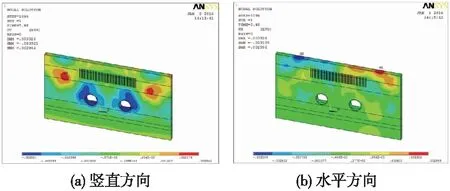
图13 监测断面地层位移云图
水平方向上,当两隧道同时作用相同列车荷载时,整体上产生的地层水平位移都较小,最大的水平位移出现在5.48 s,为3.11 mm。比较两隧道中间土层的水平位移分布情况可以发现,当两隧道同时存在列车荷载作用时,两隧道会产生相互靠近的趋势。
地层监测点B1~B5、C1~C4位移时程曲线如14所示。B1~B5位于左右两隧道对称平面内,C1~C4位于右线隧道中心线所在的竖直平面内。从整体上看,在列车荷载作用下,地层各深度处的竖向位移时程曲线差异较大,位于地表位置B1、C1处振动幅值明显大于其他深度处的地层位移,比较各监测点竖直位移时程曲线变化情况可以发现,埋深越深,振动幅值相对越小。
道床监测点竖直方向位移变化规律如图15所示,由于道床的刚度较大,列车荷载作用时,道床出现整体下沉趋势。道床各位置的竖向位移随列车振动荷载变化而变化,最大下沉值接近4.0 mm。
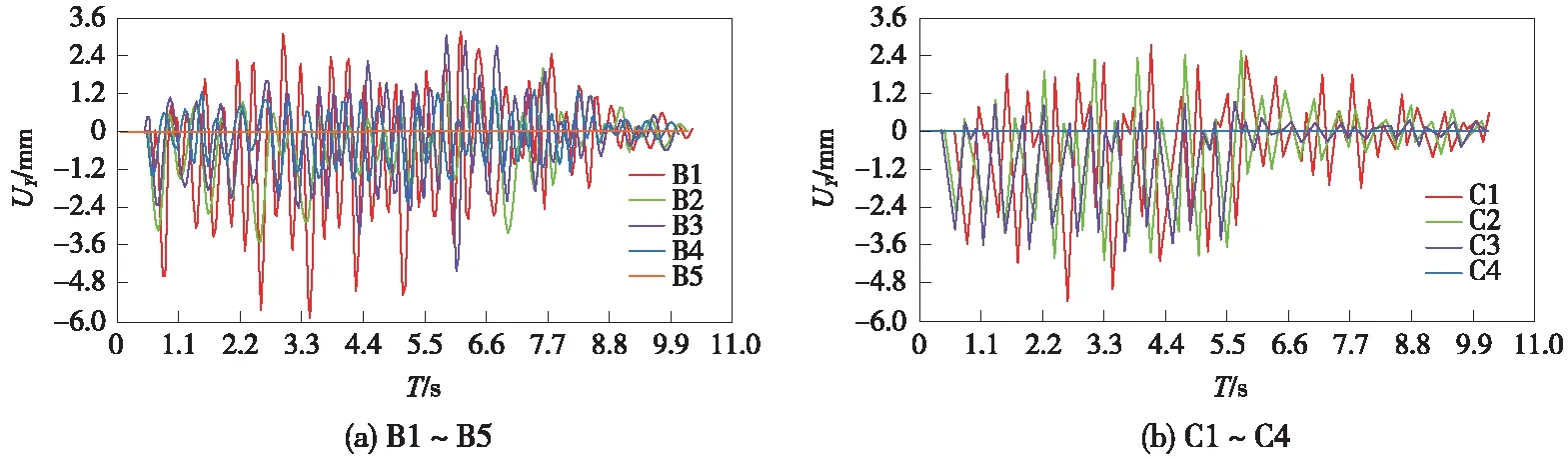
图14 地层监测点竖向位移
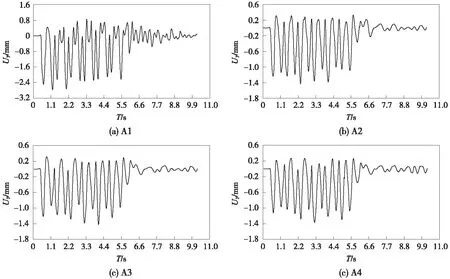
图15 道床监测点竖向位移
4.1.2 加固前长期不均匀沉降分析
根据Monismith提出的土体长期应变随加载次数变化的指数模型,结合本模型的计算结果,可得到列车荷载对隧道及周边土体长期沉降贡献值,即
EP=ANb
(4)
式中,N为加载次数,考虑到列车实际运营时间及发车时间间隔,取8×104次/年,常数b取0.17,A为第1次加载后的土体应变,通过有限元计算得到。鉴于应变与位移呈线性相关,可以采用相同的方法推广到拱底沉降的计算。拱底沉降s累计值按照下式计算。
EP=S0Nb
(5)
式中,So为第1次加载后的拱底位移,通过有限元计算得到,其余符号与公式(4)同。监测点A4的拱底沉降可以得到,在约6 s列车振动之后,整个结构还会持续振动一段时间,保守考虑6 s后拱底最大位移进行计算,未加固时6 s后拱底的最大位移为0.6 mm,取作So;计算出在未加固时,隧道70年之后的沉降量为8.42 mm。
4.2 加固后列车振动响应分析
4.2.1 加固后结构应力位移分析
为研究砂土地层加固后对衬砌结构受力和位移列车振动响应的影响规律,分别对现场采集的每立方米原状砂土加入强度等级为32.5的超细水泥,质量分别为200,300,400 kg。
加固前后管片结构、道床结构的第三主应力最大值及监测断面竖直方向与水平方向的位移最大值见表5。加固后管片结构及道床结构的主应力最大值均明显减小,其中,方案3管片结构第一主应力由1.53 MPa减少到0.29 MPa,相比减少81.0%;管片第三主应力由1.26 MPa减少到0.14 MPa,相对减少89.9%;道床结构第三主应力由1.13 MPa减至0.43 MPa,相比减少61.9%。此外,依照方案3加固地层,监测断面地层的竖直方向位移及水平方向位移分别减小了52.6%及56.3%。
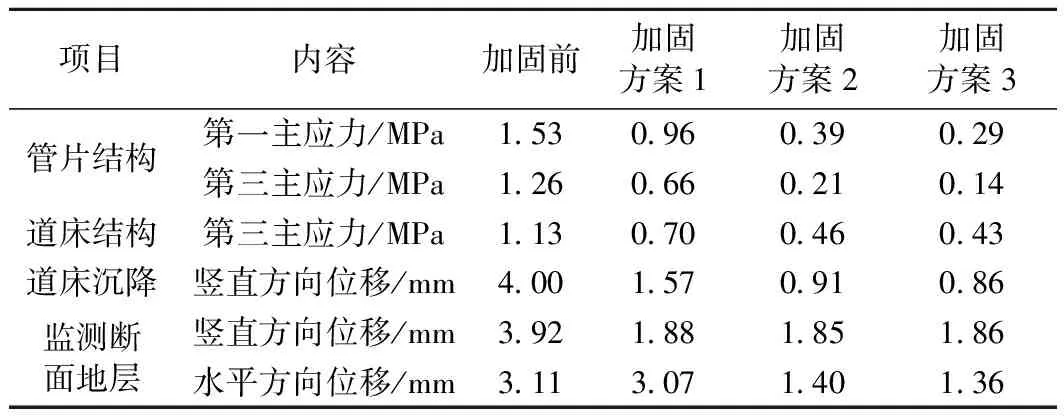
表5 各加固方案前后应力及位移对比
加固前后位移时程曲线的变化趋势基本相同,道床出现整体下沉位移,各节点竖向位移基本一致。与加固前相比,采用3种加固方案后道床的下沉量明显减少,道床监测点竖直方向位移最大下沉量分别为1.57,0.91,0.86 mm,明显小于加固前的4.0 mm最大下沉量;由于加固后地层进行了改良,C1~C4的水平、竖直方向位移都明显减少,其中方案3的水平、竖直方向位移减少均超过50%。
4.2.2 加固后长期不均匀沉降分析
通过计算得到不同加固方案6 s后拱底的最大位移分别为0.28,0.23,0.22 mm,相对于加固前明显减小。采用与加固前相同的指数模型计算得出加固前后隧道结构在列车循环荷载作用下沉降随时间的发展情况对比,加固前后沉降变化规律相似,加固后隧道结构沉降在刚开始几年内发展变化较快,随后沉降发展逐渐减缓,时间越长每年增加的沉降量越少。加固前后隧道结构沉降随时间的变化曲线如图16所示,加固前结构70年后的沉降为8.4 mm,而采取不同加固方案之后的隧道结构70年后长期沉降分别为3.9,3.2,2.85 mm。
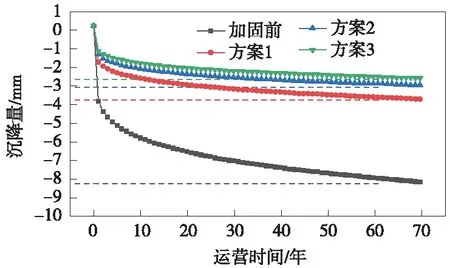
图16 加固前后隧道结构沉降随时间的变化曲线
5 结论
依托佛山地铁2号线工程,通过动三轴试验探明液化砂动力学参数对不同注浆加固方案的变化规律,并依据试验测试的动力学参数结果,建立三维有限元模型,对比分析隧道周围土体加固前后在列车振动荷载作用下的结构动力响应变化规律,主要得到以下结论。
(1)采用注浆方式对液化砂土地层进行改良加固,可有效增大土层的动剪切模量比,减小土层最大阻尼比,随着超细水泥掺量的增加,土样所能承受的动应力显著增大,砂土的抗液化性能增强。
(2)随着单位体积液化砂土地层超细水泥掺量的增加,列车振动作用下管片结构的应力及位移均明显减小,管片结构的长期沉降及周围地层竖直方向、水平方向的位移均呈递减趋势。
(3)单位体积液化砂土地层中掺加超细水泥质量为400 kg时,管片结构第一主应力、第三主应力分别减小了81%、89.9%,周围地层竖直方向、水平方向的位移分别减小了52.6%、56.3%,结构长期沉降减小67.24%,加固改良效果显著。
